|
Vedad Hadziavdic. A Comparative Study of Active Contour Models for Boundary Detection in Brain Images. Пер. с англ. Трибрат А.А.
Кривая, которая минимизирует данный энергетический функционал, должна
удовлетворять уравнению Эйлера. Чтобы решать это уравнение динамически,
рассмотрим функцию 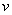 как функцию времени как функцию времени 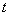 . Приравняем частную
производную . Приравняем частную
производную 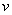 по по
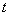 равной
левой части уравнения: равной
левой части уравнения:
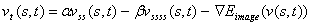 |
( 1) |
Когда решение  стабилизируется, исчезнет член стабилизируется, исчезнет член 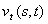 и будет
получено решение уравнения. и будет
получено решение уравнения.
Чтобы решить уравнение в численном виде, дискретизируем уравнение и решим
дискретную систему итеративно.
1. Метод конечных различий в приложении к уравнению развития snake
Основная идея метода конечных различий заключается в том, чтобы
аппроксимировать производные функции, используя конечные различающие операторы.
Если определить каждую из независимых переменных функции  на сетке, как на сетке, как
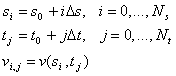 |
( 2)( 3)( 4) |
то частные
производные 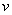 могут
быть аппроксимированы конечными различающими выражениями в направлениях могут
быть аппроксимированы конечными различающими выражениями в направлениях 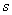 и и 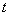 . Можно
использовать прямой оператора различия, обратный оператор различия, центральный
оператор различия, средний оператор различия, и т.д. Будем использовать в наших
вычислениях обратную различающую аппроксимацию. . Можно
использовать прямой оператора различия, обратный оператор различия, центральный
оператор различия, средний оператор различия, и т.д. Будем использовать в наших
вычислениях обратную различающую аппроксимацию.
 |
( 5) |
 |
( 6) |
и прямую различающую аппроксимацию
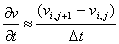 |
( 7) |
Явный конечный метод различия – вероятно, самый простой конечный метод
различия, но он не полностью удовлетворяет уравнение snake. Причина заключается в том, что метод дает полезное приближение, если выполняется
предел стабильности  , где , где 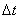 – итерационный временной шаг, – итерационный временной шаг, 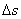 – итерационный пространственный шаг. Однако, это требование налагает серьезное ограничение на размер временного
интервала, которое приводит к существенным увеличениям вычислений. – итерационный пространственный шаг. Однако, это требование налагает серьезное ограничение на размер временного
интервала, которое приводит к существенным увеличениям вычислений.
Неявный метод конечных различий избегает вышеупомянутой проблемы и является
наиболее часто используемым в литературе.
В неявной формуле одно или больше неизвестных значений на следующем шаге
итерации определяются через известные значения на текущем шаге. Разработаем
алгоритм неявного метода конечных различий для уравнения развития snake.
Использующие операторы конечных различий, определенные в уравнениях ( 5), ( 6), ( 7), получим следующую
аппроксимацию уравнения (9.1):
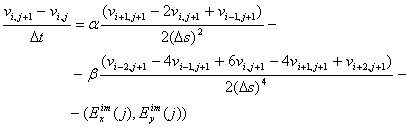 |
( 8) |
где
 |
( 9) |
Этот метод называют обратным методом Эйлера. После некоторых преобразований получим
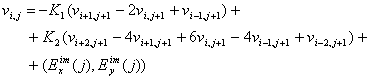 |
( 10) |
где
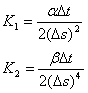 |
( 11) |
и далее
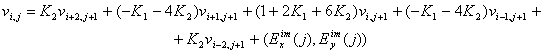 |
( 12) |
Это уравнение можно записать в матричной форме
 |
( 13) |
или как матричную систему
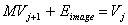 |
( 14) |
где
 |
( 15) |
Уравнение хорошо подходит для решения итеративными методами или
непосредственно матричного решения. Однако более важно, что это уравнение
одинаково для всех значений  и и 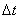 . Единственные ограничения на
выбор шага накладываются точностью и необходимым временем вычисления. . Единственные ограничения на
выбор шага накладываются точностью и необходимым временем вычисления.
Итерационное уравнение имеет следующий вид
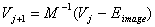 |
( 16) |
| 



