| |
Імітаційний метод визначення навантаження
промислових електричних мереж
Бєляєв Д.В., керівник: к.т.н., доцент Погрєбняк Н.М.
В основі проекту електропостачання промислових підприємств лежить розрахунок електричних навантажень, за яким здійснюється вибір необхідних перетинів провідників, комутаційної й захисної апаратур, що дозволяє спроектувати мережу електропостачання й оцінити електромагнітну сумісність (ЕМС) електроприймачів (ЕП). Промислові підприємства споживають біля двох третин вироблюваної електроенергії, тому вимоги до точності розрахунків навантажень досить великі. Їх результат позначається на техніко-економічних показниках системи (завищення електричних навантажень веде до збільшення капіталовкладень, заниження може призвести до виникнення аварійної ситуації, додатковим втратам електроенергії, збитку через електромагнітну несумісність ЕП), а в цілому на ефективність роботи підприємства, його економічні показники й конкурентноздатність.
Численні дослідження показали, що розрахункові навантаження завишають, це призвело до істотного збільшення капіталовкладень у мережі електропостачання. Збиток же від порушення ЕМС становить порядку сотень мільйонів гривень у рік. Звідси виникає необхідність досліджень в області електричних навантажень й, у першу чергу, необхідність удосконалювання діючих Вказівок до їх розрахуну.
Емпіричні методи розрахунку почали розроблятися ще в тридцяті роки (Копитов Н.В., Тіхонов В.П. й ін.). За рубежем інтерес до методів розрахунку електричних навантажень з'явився після початку Другої світової війни (Adams C.A., Fetcher J.R., Johnson A.C., Adler H.A., Miller K.W., Boice W.K.). Однак істотні результати були досягнуті в шістдесяті роки за рахунок використання імовірнісних методів аналізу випадкових величин (Каялов Г.М., Гнеденко Б.В., Волобринский С.Д., Мукосєєв Ю.Л. й ін. [3, 4] ). Остаточно методологічний підхід сформувався в рамках концепції випадкових процесів. При цьому складність і нелінійність задач електропостачання вимогали використання методів імітації випадкових процесів
З 1992 р. і по теперішній час при проектуванні систем електропостачання (СЕС) розрахунок електричних навантажень виконують по діючих Вказівках [2], в основу яких покладений модифікований статистичний метод (МСМ) [1]. Використання його замість методу впорядкованих діаграм дозволило уникнути значного завищення розрахункових навантажень за рахунок корекції середнього значення групового навантаження. Але за розрахункове навантаження, у методі, приймається розрахунковий максимум кумулятивного процесу - осередненням на 30-ти хвилинному інтервалі групового графіка навантаження, що не відповідає фізиці процесу нагрівання провідника. Положенню статистичного методу про нормальний закон розподілу кумулятивного графіка суперечить допущення про наявність кореляційного зв'язку між його середнім значенням і стандартом. Розрахункові вирази МСМ (13) і (14) з [1] дають нескінченне значення коефіцієнта 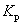 розрахункового навантаження при ефективному числі ЕП розрахункового навантаження при ефективному числі ЕП 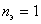 . Тому криві для визначення . Тому криві для визначення 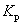 в [2], показані на мал. 1, мають непояснені перегини, хоча з ростом ефективного числа ЕП значення коефіцієнта розрахункового навантаження повинне монотонно зменшуватися в [2], показані на мал. 1, мають непояснені перегини, хоча з ростом ефективного числа ЕП значення коефіцієнта розрахункового навантаження повинне монотонно зменшуватися
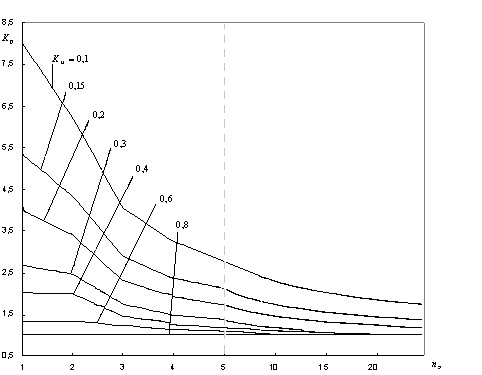
Рисунок 1 - Залежності коефіцієнта розрахункового навантаження 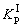 від ефективного числа ЕП від ефективного числа ЕП
Для рішення завдань із підвищеною точністю пропонуємо використати розроблений на кафедрі ЕПГ Донецького національного технічного університету, імітаційний метод розрахунку електричних навантажень
Метою розрахунку методу є визначення закону розподілу температури 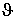 перегріву провідника, а по ньому - розрахункового навантаження. Для рішення завдання про нагрівання провідника випадковим навантаженням була прийнята запропонована професором Г.М. Каяловим [5, стор.7], [3, стор. 32] і застосовувана в теорії електричних навантажень [7, стор. 34] проста теплова модель провідника. В основу цієї моделі покладені наступні допущення: перегріву провідника, а по ньому - розрахункового навантаження. Для рішення завдання про нагрівання провідника випадковим навантаженням була прийнята запропонована професором Г.М. Каяловим [5, стор.7], [3, стор. 32] і застосовувана в теорії електричних навантажень [7, стор. 34] проста теплова модель провідника. В основу цієї моделі покладені наступні допущення:
- температура в кожній окремій точці поперечного переріза провідника практично не змінюється по його довжині;
- провідник вважається однорідним тілом з нульовим внутрішнім тепловим опором, тому що основним фактором неоднорідності будови провідника є ізоляція його жил, шар якого для напруги до 6 кв відносно невеликий.
При прийнятих допущеннях умова теплового балансу для трьохжильного кабелю, відкрито прокладеного усередині приміщення, при струмі навантаження 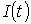 в амперах має вигляд [5, стор.7], [3, стор. 32] в амперах має вигляд [5, стор.7], [3, стор. 32]
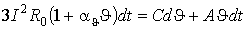 , (1) , (1)
де 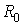 - активний опір жили провідника при температурі 20°С , Ом; - активний опір жили провідника при температурі 20°С , Ом;
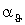 - температурний коефіцієнт опору, 1/°С; - температурний коефіцієнт опору, 1/°С;
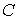 - теплоємність провідника, Дж/°С; - теплоємність провідника, Дж/°С;
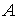 - коефіцієнт тепловіддачі, що враховує сумарну віддачу тепла в навколишнє середовище за рахунок теплопровідності, конвекції й випромінювання, Вт/°С. - коефіцієнт тепловіддачі, що враховує сумарну віддачу тепла в навколишнє середовище за рахунок теплопровідності, конвекції й випромінювання, Вт/°С.
З (1) отримане рівняння для перегріву провідника щодо навколишнього середовища
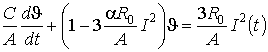 . (2) . (2)
В [5, стор.8], [3, стор.33] показано, що збільшення значення
коефіцієнта тепловіддачі практично компенсує одночасне зростання опору 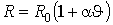 .
Тому в (2) із припустимою для .
Тому в (2) із припустимою для 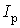 похибкою
прийнято похибкою
прийнято 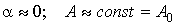 . Тоді рівняння (2) має наступний вид . Тоді рівняння (2) має наступний вид
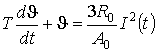 , (3) , (3)
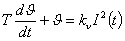 , (4) , (4)
де 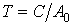 - постійна часу нагрівання провідника, - постійна часу нагрівання провідника, 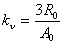 ; ;
Таким чином, до перерахованих припущень додаються ще два: постійна часи нагрівання й активний опір провідника не залежать від температури нагріву. У сталому режимі при незначних коливаннях температури це спрощення не приводить до значної похибки. Для зручності виконання розрахунків застосуємо підстановку 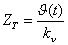 , у результаті якої рівняння (4) має наступний вид , у результаті якої рівняння (4) має наступний вид
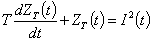 , (5) , (5)
або, стосовно до групового графіку 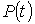 активного навантаження, активного навантаження,
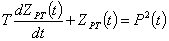 . (6) . (6)
Величина, 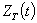 ( ( 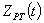 ) названа гріючою дозою, пропорційна температурі перегріву провідника й має розмірність квадрата навантаження. ) названа гріючою дозою, пропорційна температурі перегріву провідника й має розмірність квадрата навантаження.
Вихідними для визначення розрахункових навантажень є процеси зміни електричних навантажень. Професор Г.М. Каялов у методі імовірнісного моделювання для вивчення графіків навантажень уперше застосував теорію випадкових функцій й імпульсних потоків. Метод став теоретичною базою для проведення подальших досліджень. Моделювання групових графіків - результат підсумовування індивідуальних, у такий спосіб завдання зводилось до створення алгоритму моделювання індивідуального графіка.
Строга періодичність останнього формується при роботі електроприймача з максимальним навантаженням. Вивчення цього графіка, незважаючи на його малоймовірність на практиці, має теоретичне значення, тому що він відповідає граничному режиму. Складності у визначенні діапазону зміни, характеристик і закону розподілу температури нагріву провідника для періодичного імпульсного графіка вже вирішені, модель випадкового індивідуального графіка навантаження повинна бути задана:
- номінальним активним навантаженням 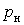 , кВт; , кВт;
- коефіцієнтом використання
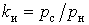 , (7) , (7)
де 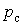 - середнє активне навантаження, кВт; - середнє активне навантаження, кВт;
- коефіцієнтом завантаження
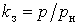 , (8) , (8)
де 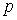 - середня потужність, споживана ЕП під час включення, кВт; - середня потужність, споживана ЕП під час включення, кВт;
- коефіцієнтом реактивної потужності 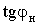 ; ;
- видом і значеннями параметрів кореляційної функції (КФ) або величиною середнього часу циклу 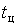 . .
Коефіцієнти включення 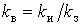 і відключення і відключення 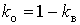 дорівнюють відповідно ймовірностям включеного і відключеного станів ЕП. дорівнюють відповідно ймовірностям включеного і відключеного станів ЕП.
У роботі прийняли індивідуальний графік активного електричного навантаження двоступінчастим: він складається з імпульсу величиною 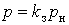 тривалістю тривалістю 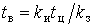 і нульовою паузою і нульовою паузою 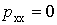 тривалістю тривалістю 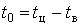 . .
У реальних умовах ЕП працюють із деякої, але не строгою періодичністю. Тому КФ індивідуального навантаження може бути аппроксимований виразом
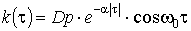 , (9) , (9)
де 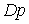 - дисперсія індивідуального графіка навантаження; - дисперсія індивідуального графіка навантаження;
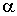 - параметр
КФ, зворотний часу кореляції, с-1 - параметр
КФ, зворотний часу кореляції, с-1
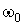 - частота періодичної складової, с-1. - частота періодичної складової, с-1.
По опублікованим нормованим КФ індивідуальних графіків активної потужності 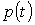 , отриманим експериментально в діючих системах електропостачання, видно, що для індивідуальних графіків навантажень, в основному, характерна експоненциально-косинусоідальна КФ. , отриманим експериментально в діючих системах електропостачання, видно, що для індивідуальних графіків навантажень, в основному, характерна експоненциально-косинусоідальна КФ.
Параметри КФ можуть бути визначені як експериментально, так і з технологічних розрахунків. В останньому випадку індивідуальне навантаження представляють у вигляді імпульсного процесу, дисперсію й параметри КФ якого можна визначити по формулах:
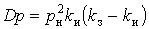 , , 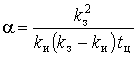 , , 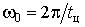 . (10) . (10)
Переходячи до моделі групового графіка, відзначимо, що незважаючи на нестаціонарність добового графіка навантаження, на ньому можна виділити ділянки, на яких груповий графік є стаціонарним ергодично випадковим процесом.
Достоїнством моделі є те, що характеристики групового графіка навантаження визначаються по відомих характеристиках індивідуальних графіків відповідно до формул для числових характеристик суми випадкових функцій.
Для групи масових ЕП властива індивідуальним графікам навантаження періодичність у груповому графіку практично не проявляється, тому в теорії електричних навантажень зокрема, у методах імовірнісного моделювання й інерційному, прийнято, що КФ групового графіка має вигляд
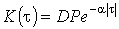 , (11) , (11)
де 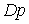 -дисперсія групового графіка навантаження. Прийнята модель групового навантаження з експонентної КФ забезпечує деякий запас при визначенні розрахункових навантажень. -дисперсія групового графіка навантаження. Прийнята модель групового навантаження з експонентної КФ забезпечує деякий запас при визначенні розрахункових навантажень.
Коефіцієнт форми, дорівнює відношенню ефективного 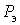 навантаження до середнього навантаження до середнього 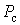 : : 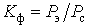 , характеризує нерівномірність графіка навантаження. , характеризує нерівномірність графіка навантаження.
Розглянемо закон розподілу ординат групового графіка. Представивши індивідуальне навантаження у вигляді імпульсного процесу, функцію розподілу групового навантаження можна розрахувати, використовуючи теорему про повторення дослідів. Кількість одночасно працюючих ЕП і групове навантаження при однакових величинах імпульсів всіх ЕП підкоряється біноміальному закону розподілу. Звичайно значення імпульсів окремих ЕП різні. У цьому випадку закон розподілу навантаження умовно будемо називати “комбінаторним”.
Академік Б.В. Гнеденко теоретично довів, що нормальний закон розподілу навантаження можна вважати справедливим для магістралей, що живлять більше 6 ЕП. Таким чином, у роботі приймемо, що групове навантаження розподілене нормально, а у випадку невеликої кількості ЕП і при наявності випадаючих з ряду по потужності або режиму роботи ЕП закон імовірнісного розподілу навантаження будемо називати комбінаторним і розраховувати по теоремі про повторення дослідів.
Алгоритм імітаційного методу визначення розрахункового навантаження включає наступні етапи:
- імітація ансамблю реалізацій групового графіка струму навантаження 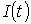 або активної потужності або активної потужності 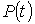 ; ;
- розрахунок ансамблю реалізацій гріючої дози 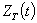 ( ( 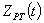 ) відповідно до інтеграла Дюамеля ) відповідно до інтеграла Дюамеля
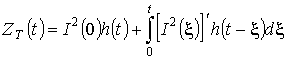 , (12) , (12)
де 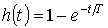 - перехідна функція інерційної ланки. - перехідна функція інерційної ланки.
- розрахунок статистичної функції розподілу гріючої дози, по перетині отриманого ансамблю 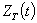 ( ( 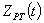 ), узятому після загасання перехідного процесу нагрівання провідника в момент часу ), узятому після загасання перехідного процесу нагрівання провідника в момент часу 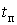 ; ;
- визначення розрахункового максимального значення грієючої дози 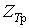 або або 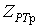 із заданою граничною ймовірністю із заданою граничною ймовірністю 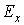 відповідно до принципу практичної впевненості по статистичній функції розподілу гріючої дози, відповідно до принципу практичної впевненості по статистичній функції розподілу гріючої дози, 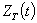 ( ( 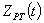 ) )
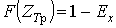 або або 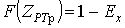 ; (13) ; (13)
- визначення розрахункового навантаження по струму 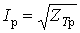 або по активній потужності або по активній потужності 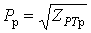 . .
Імітаційний метод був застосований для визначення статистичних закономірностей [9], на підставі яких розроблений інженерний метод гріючої дози (ГД) [13]. Цей метод має більш високу точність, ніж МСМ. На його основі складений проект Вказівок з розрахунку електричних навантажень промислових підприємств ВАТ «Київпромелектропроект» для апробації, і широко використовується в науково-дослідній роботі студентів.
Недоліком імітаційного методу є спрощення в реалізації: реактивне навантаження розраховується за допомогою інженерного методу, що не відповідає ідеї імітаційного методу й веде до зниження точності розрахунків. Тому був запропоний вдосконалений імітаційний метод, температура перегріву провідника відповідно до якого визначається по повному навантаженню. Для визначення розрахункового навантаження вдосконаленим імітаційним методом імітується ансамбль реалізацій групового графіка повного навантаження. Кількість реалізацій ансамблю, необхідне для одержання достовірного значення розрахункового навантаження визначається статистичними методами й становить порядку 5-10 тисяч.
Тривалість кожної реалізації визначається часом закінчення перехідного процесу нагрівання провідника з постійною часу нагріву Т и приймається рівною 5Т.
Для отримання однієї реалізації групового графіка навантаження моделюються індивідуальні графіки активного й реактивного навантажень кожного електроприймача. Групові графіки активного й реактивного навантажень отримують шляхом підсумовування відповідних індивідуальних графіків. По групових графіках активного й реактивного навантажень визначається груповий графік повного навантаження.
Використовуючи інтеграл Дюамеля, по ансамблю реалізацій групового графіка повного навантаження розраховується ансамбль реалізацій гріючої дози.
Для визначення розрахункового значення гріючої дози, по перетину її ансамблю, узятому після завершення перехідного процесу нагрівання провідника розраховується статистична функція розподілу.
По статистичній функції розподілу грючої дози, визначаємо її розрахункове максимальне значення (значення, що може бути перевищене з імовірністю 0,05). Розрахункове повне навантаження дорівнює квадратному кореню з гріючої дози.
Графічно, роботу програми можна проілюструвати в такий спосіб (Рисунок 1.1):

Рисунок 1.1- Метод розрахунку навантаження уточненим імітаційним методом
Складена програма що дозволяє розрахувати навантаження кожної ділянки електричної мережі будь-якої конфігурації уточненим імітаційним методом. Також програма може застосовуватися для моделювання реалізацій групових графіків електричних навантажень, при оцінці точності існуючих і розробляємих інженерних методів розрахунку електричних навантажень
Недоліком методу є значна тривалість розрахунку, оскільки необхідна точність досягається імітацією великої кількості реалізацій графіків електричного навантаження
ПЕРЕЛІК ВИКОРИСТАНИХ ДЖЕРЕЛ
1. Жохов Б.Д. Анализ причин завышения расчетных нагрузок и возможной их коррекции // Промышленная энергетика. - 1989. - №7. - С.17-21
2. Руководящий технический материал. Указания по расчету электрических нагрузок: РТМ 36.18.32.4-92: Утв. ВНИПИ Тяжпромэлектропроект: Введен с 01.033 / Инструктивные и информационные материалы по проектированию электроустановок. – М.: ВНИПИ Тяжпромэлектропроект, 1992. – № 6-7. – С. 4-27.
3. Электрические нагрузки промышленных предприятий / С.Д. Волобринский, Г.М. Каялов, П.Н. Клейн, Б.С. Мешель. - Л.: Энергия, 1971. - 264 с.
4. Волобринский С.Д. Электрические нагрузки и балансы промышленных предприятий. – Л.: Энергия, 1976. – 128 с.
5. Основы построения промышленных электрических сетей / Г.М. Каялов, А.Э. Каждан, И.Н.
6. Ковалев. Э.Г. Куренный / Под ред. Г. М. Каялова. - М.: Энергия, 1978. - 352 с.
Шидловский А.К., Куренный Э.Г. Введение в статистическую динамику систем электроснабжения. - К.: Наукова думка, 1984. - 271 с.
7. Жежеленко В.И., Саенко Ю.Л., Степанов В.П. Методы вероятностного моделирования в расчетах характеристик электрических нагрузок потребителей. - М.: Энергоатомиздат, 1990. -128 с.
8. Куренный Э.Г., Дмитриева Е.Н., Погребняк Н.Н. Совершенствование методов расчета электрических нагрузок // Промислова електроенергетика та електротехніка. Інформаційний збірник. - К.: ТОВ «ЕТІН». - 1997. - Випуск 4. – С. 14-28.
9. Погребняк Н.Н. Статистические решения нелинейных задач теории электрических нагрузок сетей электроснабжения промышленных предприятий. // Сборник научных трудов ДонГТУ. Серия: электротехника и энергетика, выпуск 4 - Донецк: ДонГТУ. - 1999. - С. 173-176.
10. Погребняк Н.Н. Анализ режимов сетей электроснабжения имитационными методами // Энергетика и электрификация. - 1999. - №2. - С. 22-24.
11. Погребняк Н.Н. Решение задач электроснабжения путем имитации ансамбля реализаций случайных процессов // Сборник научных трудов ДонГТУ. Серия: электротехника и энергетика, выпуск 2 - Донецк: ДонГТУ. - 1998. - С. 67-73.
12. Курінний Е.Г, Погрібняк Н.М. Інерційне енергетичне згладжування випадкових електричних процесів // Технічна електродинаміка. - 1999. - №3. - С. 54-58.
13. Погребняк Н.Н. Совершенствование методов определения расчетных электрических нагрузок по нагреву // Збірник наукових праць ДонДТУ. Серія: “Електротехніка і енергетика”, випуск 17: Донецьк: ДонДТУ, 2000. – С. 146-149.
14. Руководящий технический материал. Указания по расчету электрических нагрузок: РТМ 36.18.32.4-92: Утв. ВНИПИ Тяжпромэлектропроект: Введен с 01.033 // Инструктивные и информационные материалы по проектированию электроустановок. – М.: ВНИПИ Тяжпромэлектропроект. – 1992. – № 6-7. – С. 4-27.
|

