Потапенко Е.М, Потапенко Е.Е., Кулинич Э.М. Запорожский национальный технический университет, Украина

Вступление

Опыт эксплуатации асинхронных двигателей с короткозамкнутым ротором (АД) показывает, что такие нелинейности, как насыщение магнитной цепи и ограничения по току и напряжению статора, оказывают существенное влияние на динамические и статические характеристики АД. Имеются работы [1-4], где проведены аналитические исследования режимов векторного управления АД, когда токи и (или) напряжения находятся на ограничениях. Однако при дополнительном учете магнитного насыщения исследования проводились только путем численного моделирования.

В работе [5] авторами была предложена новая простая, но точная математическая модель насыщения магнитной цепи. Там же с учетом этой модели аналитически синтезированы оптимальные программные составляющие статорного тока в синхронной системе координат, минимизирующие его модуль при векторном управлении. Были получены энергетические и динамические характеристики для случая, когда модуль статорного тока i меньше imax ( imax- ограничение тока). При этом ограничение по статорному напряжению не учитывалось. Это ограничение оказывает существенное влияние при больших скоростях ротора АД, когда сильно влияние противоЭДС.

Целью данного исследования является синтез составляющих в синхронной системе координат программного статорного тока, минимизирующих модуль статорного напряжения при заданном электромагнитном моменте с учетом насыщения магнитной цепи АД и ограничения по току и напряжению при большом модуле скорости ротора АД.

Оптимизация системы при работе с большими скоростями

При больших скоростях ротора АД падением напряжения на активном сопротивлении статора можно пренебречь по сравнению с противоЭДС. Тогда в стационарном режиме можно полагать, что проекции напряжения (u) и тока (i) статора АД в синхронной системе координат (d,q) связаны соотношениями [1-4].

а электромагнитный момент (m) определяется выражением

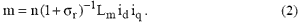
В (1) и (2) w₀ - синхронная частота (скорость вращения вектора потокосцепления ротора в статорной системе координат); n- количество пар полюсов; G ,G_r- коэффициенты рассеивания всего АД и ротора; id,iq - намагничивающая и моментная составляющие тока; Lm ,Ls-взаимная индуктивность статора и ротора и индуктивность статора. В соответствии с [5]

индекс “0” указывает на значения индуктивностей на линейном участке кривой намагничивания, индекс “ r”- соответствует ротору, “ s”- статору, “ m ”-взаимной индуктивности, a- эмпирическая константа. При не учете насыщения магнитной цепи следует полагать a=0.

Ограничение по напряжению зададим в виде

Подстановка (1) с учетом (3) в (4) дает уравнение

При фиксированном |u| и малых id или при пренебрежении магнитным насыщением (a=0) уравнение (5) на плоскости (id,iq) описывает набор эллипсов, вытянутых из-за соотношения G < 0,1 вдоль оси 0iq (рисунок). Каждый из эллипсов соответствует определенному значению w₀ . Эллипсы, соответствующие большим значениям w₀ , лежат внутри эллипсов с меньшими значениями w₀ . Т.к. id >=0 , то рабочей зоной является правая полуплоскость. Как следует из (5), влияние магнитного насыщения проявляется в вытягивании эллипсов вдоль оси 0id .

С помощью (2), (3) исключим iq из (5). Тогда

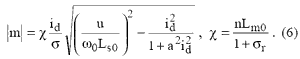
Поскольку дискриминант в (6) не должен быть отрицательным, то должно выполняться соотношение

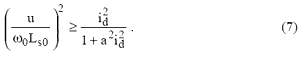
Экстремальные значения m в зависимости от id можно найти из выражения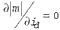или, что то

Рисунок 1

же самое, из выраженияВторое равенство дает уравнение

откуда

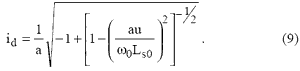
Из (9) следует, что

По выражениям (5) и (9) можно получить

Как следует из (9), (11), при возрастании |w₀| и фиксированном u id,iq стремящемся к 0. При достаточно малом 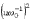можно записать

Приближенные выражения (12), (13) совпадают с точными выражениями работ [1,2], полученными без учета магнитного насыщения. (Выражение id без учета насыщения можно получить из (8) при a = 0).

Подстановка (9), (11) в (2) с учетом (3) дает зависимость экстремальных значений электромагнитного момента от напряжения статора и синхронной скорости w₀ в виде

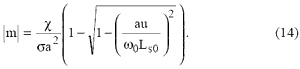
Из (14) видно, что за счет ограничения напряжения соотношением (4) электромагнитный момент также будет ограничен. Причем максимальное значение m будет тем меньше, чем больше будет w₀ . При малом 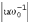путем применения разложения бинома можно получить

Если пренебречь магнитным насыщением, то приближенное равенство (15) становится точным.

Потребляемые полная (P) и электромагнитная (Pem ) мощности могут быть определены с помощью выражений (28) работы [6], (9), (11). При пренебрежении магнитным насыщением с использованием (12), (13), (15) можно получить

где w -механическая угловая скорость ротора,

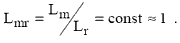
Поскольку nw приблизительно равно w₀ , то с учетом выражения X из (6) развиваемая механическая мощность

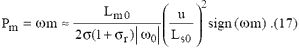
Как видно из (15)-(17), электромагнитный момент и мощность ( с точностью до потерь в железе) обратно пропорциональны квадрату, а механическая мощность первой степени синхронной скорости. Подстановка в выражения (9)-(17) значения |u| = umax позволяет определить предельные значения соответствующих переменных. Следует отметить на основании (16), что без учета потерь в стали мощности, рассеиваемые в статоре и роторе, пропорциональны между собой.

Выражения проекций тока (9), (11) зависят от статорного напряжения u. Для осуществления управления АД необходимо иметь их зависимости от потребного электромагнитного момента m . Для установления связи между u и m можно воспользоваться равенством (14), откуда

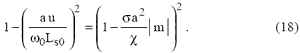
Подстановка (18) в (9), (11) дает искомые зависимости проекций токов от потребных электромагнитных моментов в виде

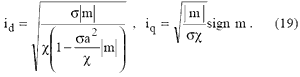
На основании (14) имеет место следующее ограничение электромагнитного момента:

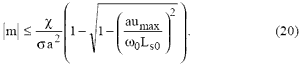
В (19), m - потребное значение электромагнитного момента, ограниченное соотношением (20), а сами выражения (19) обеспечивают минимум модуля напряжения при заданном электромагнитном моменте. При малом |m| или при a =0

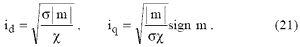
Интересным является то, что id и iq из (19), (21) не зависят от скорости, а iq не зависит от магнитного насыщения. Магнитное насыщение увеличивает ток id .

Как следует из выражения id в (19), магнитное насыщение накладывает следующее ограничение на электромагнитный момент:

Выражения (19) и (28) работы [6] дают выражения мощностей с учетом магнитного насыщения, а именно,

(При получении (22) пренебрегли потерями в железе).

Таким образом, электромагнитная, механическая и полная мощности пропорциональны модулю электромагнитного момента.

В соответствии с (32) работы [6] и (19) для установившегося режима абсолютное скольжение

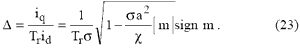
С учетом того, что G < 0.1, сравнение (23) с (32) работы [6] показывает, что при больших |w₀| модуль оптимального скольжения во много раз больше, чем модуль оптимального скольжения при малых |w₀| .

Работа системы при ограничениях напряжения и тока

В этом режиме также можно пренебречь падениями напряжения на активном сопротивлении статора по сравнении с противоЭДС. Ограничение по току описывается уравнением

Решая совместно уравнения (5) при |u| = umax и (24), получим

Выражения (25), (26) накладывают следующие ограничения на реализуемость рассматриваемого режима работы:

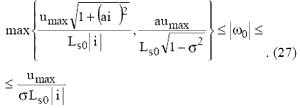
Сравним члены в фигурных скобках в (27), учитывая, что они оба положительные.

Таким образом, знак разности определяется знаком разности 1-G²(1+a²i²), которая всегда положительная. Следовательно, система неравенств (27) сводится к системе

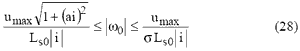
Выражения (25), (26) не устанавливают связь между необходимым электромагнитным моментом и токами id, iq . Для устранения этого недостатка учтем, что для подавляющего большинства АД G гораздо меньше 0.1. С учетом этого в (25) пренебрежем членами, пропорциональными G². Тогда

iq найдем из (2) с учетом (3), а именно, из выражения

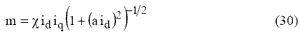
в виде

При этом должно выполняться неравенство, следующее из (24)

Выражения (29), (31) при a = 0 (без учета магнитного насыщения) совпадают с широко распространенными выражениями намагничивающего и моментного токов в режиме ослабления магнитного потока. Приравнивая (26) и (31), можно найти соответствующее выражение i. Таким образом, траектория (29), (31) с точностью до ? 2удовлетворяет траектории, соответствующей соотношениям (5) при |u| = umax и (24), то есть они с точностью до G² эквивалентны траектории (25), (26).

Выводы

1.Синтезированы простые выражения (19), (20), позволяющие формировать заданный электромагнитный момент с минимальным по модулю статорным напряжением с учетом насыщения магнитной цепи и ограничения напряжения.

2.Получены выражения (29), (31), (32), обеспечивающие формирование заданного электромагнитного момента с учетом насыщения магнитной цепи и ограничений по току и напряжению.

ЛИТЕРАТУРА

1. Novotny D.W. and Lipo T.A. Vector Control and Dynamics of AC Drives.-Oxford: Clarendon Press,1996.-440p.

2. Vas P. Sensorless Vector and Direct Torque Control. Oxford:Oxford University Press, 1998.-729p.

3. Novotnak R.T., Chiasson J. and Bodson M. HighPerformance Motion Control of an Induction Motor with Magnetic Saturation// IEEE Trans. Contr. Syst. Techn.-1999.-V.7,N3.-p.315-327

4. Jul-Ki Seok and Seung-Ki Sul. Optimal Flux Selection of an Induction Machine for Maximum Torque Operation in Flux-Weakening Region// IEEE Trans. on Power Electronics.-1999.-V.14,N4.-p.700-708.

5. Потапенко Е.Е., Потапенко Е.М. Синтез оптимальных алгоритмов управления асинхронным приводом с учетом нелинейностей//Вестник НТУ «ХПИ» Харьков. Сер. «Электротехника, электроника, электропривод».-2001.-Вып.10.-с.107-110.

6. Потапенко Е.Е., Потапенко Е.М. Синтез экстремального робастного управления асинхронным приводом // Технічна електродинаміка. Тематичний випуск “Проблеми сучасної електротехніки”. Част.6.-Київ: Ін-т електродинаміки, 2000.-с.34-36.