ПОРІВНЯЛЬНИЙ АНАЛІЗ ПАРАМЕТРИЧНОЇ ЧУТЛИВОСТІ РІЗНИХ СХЕМ ВЕКТОРНОГО КЕРУВАННЯ ЕЛЕКТРОПРИВОДОМ ЗМІННОГО СТРУМУ

Підвищення вимог щодо якості роботи системи в перехідних та усталених режимах призводить до поступового витіснення традиційних частотно-керованих асинхронних електроприводів системами векторного керування. Завдяки інтенсивному розвитку напівпровідникових пристроїв та широкому впровадженню мікропроцесорної техніки системи векторного керування стали промисловим стандартом електроприводу змінного струму. Велика кількість розроблених алгоритмів векторного керування вимагає проведення їх класифікації щодо чутливості до параметричних збурень та точності ідентифікації координат стану. Такий аналіз дасть змогу формувати вимоги щодо використання тих чи інших структур регуляторів та естиматорів координат стану залежно від вимог щодо якісних характеристик електроприводу, що диктуються умовами роботи самого об’єкту. Нажаль, на сьогоднішній день, як свідчить огляд літературних джерел, відсутній єдиний критерій для проведення порівняльного аналізу різних схем електроприводу з векторним керуванням. Традиційно, дослідники для аналізу чутливості керованого електроприводу до параметричних змін проводять експерименти на фізичних або математичних моделях системи. Зокрема, в роботі [4] чутливість частотно-струмового векторного приводу до неточності задання параметрів регулювання визначена за допомогою експериментально знятих залежностей, а в роботі [5] показані зміщення нулів та полюсів залежно від зміни параметрів та координат системи електроприводу на основі фізичної моделі GTO-CSI інвертора з регулюванням ковзання. В той же час провідними науковцями в галузі чутливості систем керування (Е.Н. Розенвассер, Р.М. Юсупов, [1], Р. Томович [3]) розроблено значну кількість аналітичних методів знаходження міри чутливості як оціночного критерія для проведення порівнянь. Проте, на сьогоднішній день відсутні рекомендації щодо однозначного вибору аналітичного методу для дослідження систем електроприводу.

Таким чином, для ефективного порівняння параметричної чутливості в системах з векторним керуванням (системи в цілому, її окремих контурів, спостерігачів, і т.д.) необхідним є математичний апарат, що давав би змогу оцінювати чутливість систем як на етапі їх проектування так і при зміні структури, без створення для цього спеціальних моделей. Для цього нами пропонується використовувати алгоритм знаходження параметричної чутливості лінійних систем, який набув широкого застосування в теоріях оптимізації та цифрової фільтрації [6]. Для системи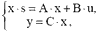(1) так звана L²-чутливість визначається, як:

де i=1,2,3,… ; delta – дискретний період при апроксимації функції .

Матриці K_0,1,2,…і W_0,1,2,… визначаються з систем рівнянь:

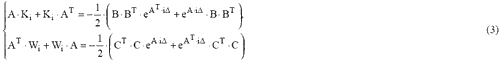
А для знаходження чутливості системи (1) до зміни окремого параметру (припускаючи що ця зміна не залежить від частоти) пропонується оцінювати дисперсію передавальної функції наступним чином:

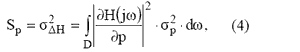
де H(jw) - комплексна передавальна функція системи (1); p - змінний параметр; G²_p - дисперсія параметра, D –частотна область системи.

Параметричні збурення зі сторони двигуна в системі електроприводу, виникають з відомих причин: зміна активних опорів обмоток внаслідок тривалих перевантажень; збільшення втрат в сталі при високих частотах перемагнічування; зміна індуктивних опорів заступної схеми АД при насиченні контуру намагнічування або зубцевих зон.

В системах векторного керування традиційно використовуються ПІ-, П- та гістерезисні регулятори. Системи електроприводу з векторним керуванням в спрощеному вигляді можна представити як двоконтурну систему [2] (рис.1), з відповідними регуляторами. У випадку гістерезисного регулятора струму, для ковзного режиму роботи та при малій зоні нечутливості його роботу можна представити пропорційною ланкою з нескінчено великим коефіцієнтом підсилення.

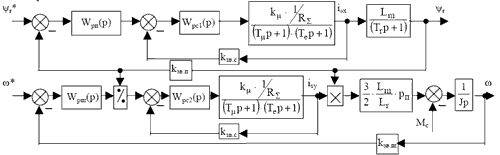
Рис.1. Спрошена структурна схема системи регулюання потоку та швидкості асинхронного електропривода при традиційному векторному керуванні (DFOC) з орієнтацією за вектором потокозчеплення ротора

Для проведення досліджень використано параметри двигуна P=7,5 кВт, Uн=220В, pп=2, Iн=16,5А. Результати розрахунків подано у табл.1.

Отримані результати підтверджують наведені в літературі дані та співвідношення чутливості систем векторного керування до зміни параметрів [5]. Як і очікувалось, система векторного керування з гістерезисними регуляторами струму є менш чутливою до зміни параметрів, що підтверджується як і критерієм на основі і L2-чутливості, так і чутливістю системи до зміни окремих параметрів. Дані результати можуть бути розповсюджені і на аналіз чутливості систем DTC (Direct Torque Control), в яких застосовано гістерезисні регулятори і на систему непрямого векторного керування (IFOC), яку можна представити, як традиційну плюс нелінійні зв’язки для задання та визначення окремих координат через параметри двигуна. Це призведе до підвищення чутливості системи IFOC до параметричних збурень у порівнянні з DFOC.

Нами пропонується метод L2-чутливості використовувати також і для порівняння параметричної чутливості різного роду спостерігачів, які широко застосовуються в усіх вищезгаданих системах векторного керування. Це дасть можливість здійснювати вибір структури спостерігача, що максимально задовольнятиме вимоги зі сторони системи керування електроприводом. Такі дослідження планується провести в подальшій роботі.

Література

1. Е.Н. Розенвассер, Р.М. Юсупов. Чувствительность систем автоматического управления. Л., «Энер- гия»,1969.

2. „Теорія електропривода”. За ред. М.Г. Поповича. – Київ, «Вища школа», 1993.

3. Р. Томович, М. Вукобратович. Общая теория чувствительности. М., «Советское радио», 1972, 240 с.

4. Поздеев А.Д. ”Чувствительность асинхронных регулируемых электроприводов с частотно-токовым век- торным управлением к неточности задания параметров настройки.” – Электротехника, №6, 1998р., ст. 1-7.

5. B. Wu, G. R. Slemon, S.B. Dewan, “Eigenvalue sensitivity analysis of GTO-CSI induction mashine drives”. IEEE Trans. on Industry Applications , vol.30, NO. 3, pp. 767-775, May 1994.

6. T. Hinamoto, S. Yokoyama, T. Inoue, W. Zeng W.-S. Lu, “Analysis and minimization of L2-Sensitivity for linear systems and two-dimensional state-space filters using general controllability and observability Gramians”. IEEE Trans.Circuits Syst., vol.49, pp. 1279-1289, Sept. 2002.