

| <<< Предыдущая | Вернутся к Библиотеке |   |
Работа VSI привода от источника переменной частоты
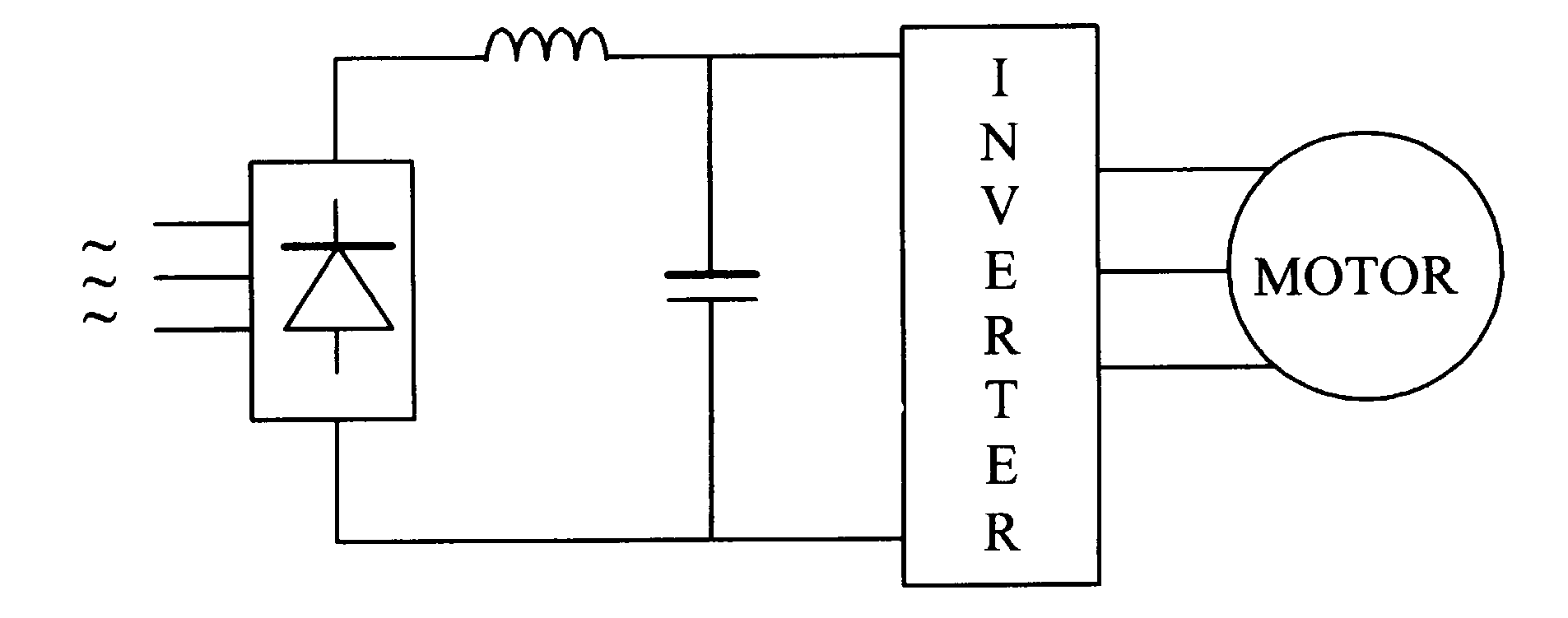
Уравнения крутящего момента 6.28, 6.33 и 6.34, предыдущих разделов, описывают двигательный режим работы синхронного двигателя при питании его от источника регулируемого напряжения и переменной частоты. Для последующих исследований предположим, что питание трехфазным синусоидальным переменным током, непрерывно изменяющегося среднеквадратического выходного напряжения и частоты, происходит от инвертора, как показано на принципиальной схеме, рисунок 6.17.
Пренебрегая сопротивлением статора R, выражение крутящего момента 6.28 можно записать как
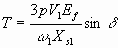 6.34
6.34
где
ω1 = переменная угловая частота, 2pf, (электрическая) при питании двигателя от источника переменного токаV1 =
среднеквадратическое напряжение при питании двигателя от источника переменного тока, при частоте f1Xs1
= синхронное реактивное сопративление, 2pf1 Ls двигателя при частотном питании.Из уравнение 6.34 видно, что развиваемый момент пропорционален приложенному действующему напряжению, и его максимальное значение достигается при
δ=90°. Так как механическое быстродействиеЭто означает, что такой же максимальный крутящий момент достигается, если соотношение
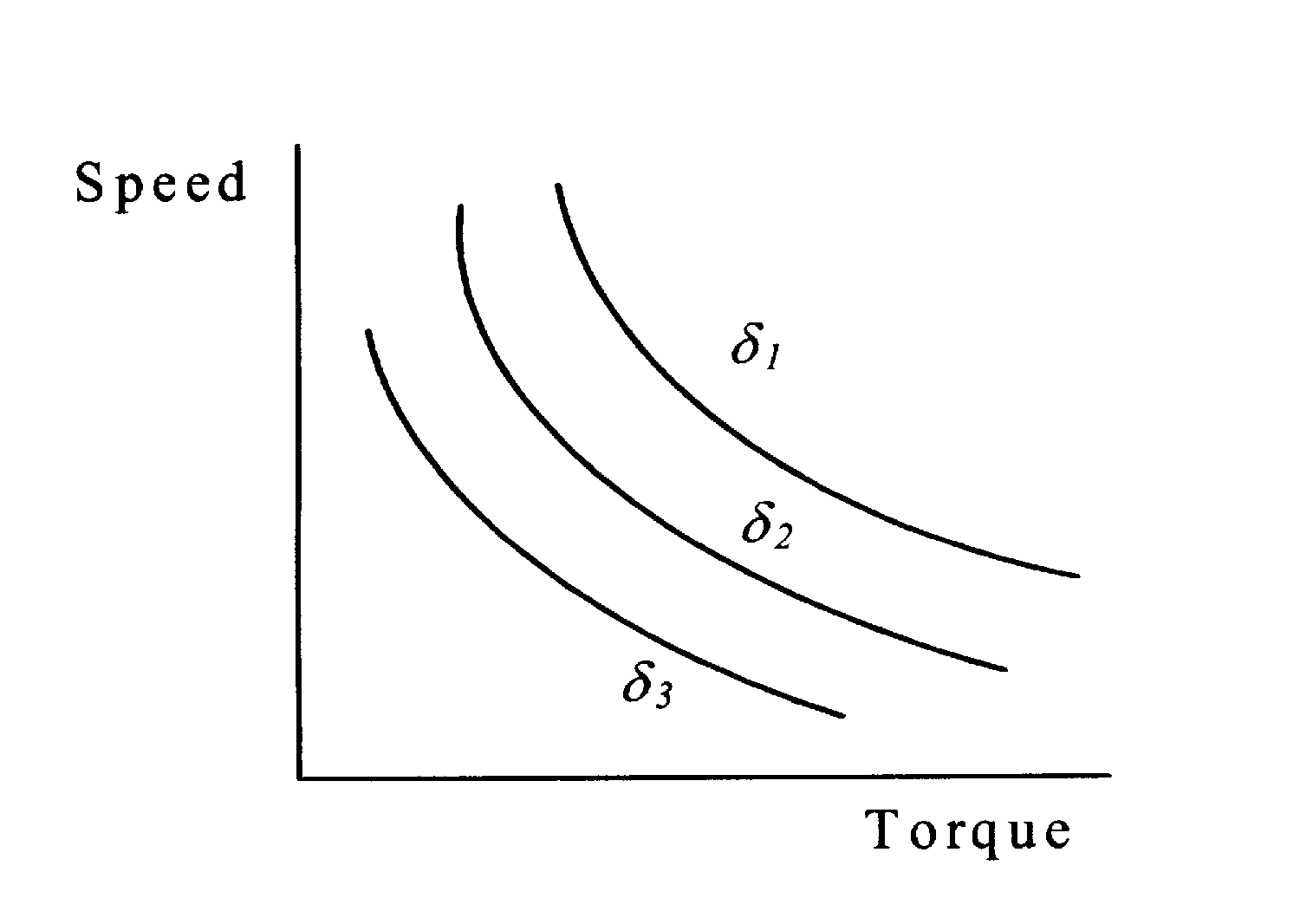
Типичные
T-ω характеристики при регулируемом напряжении и переменной частоте представлены на рисунке 6.18.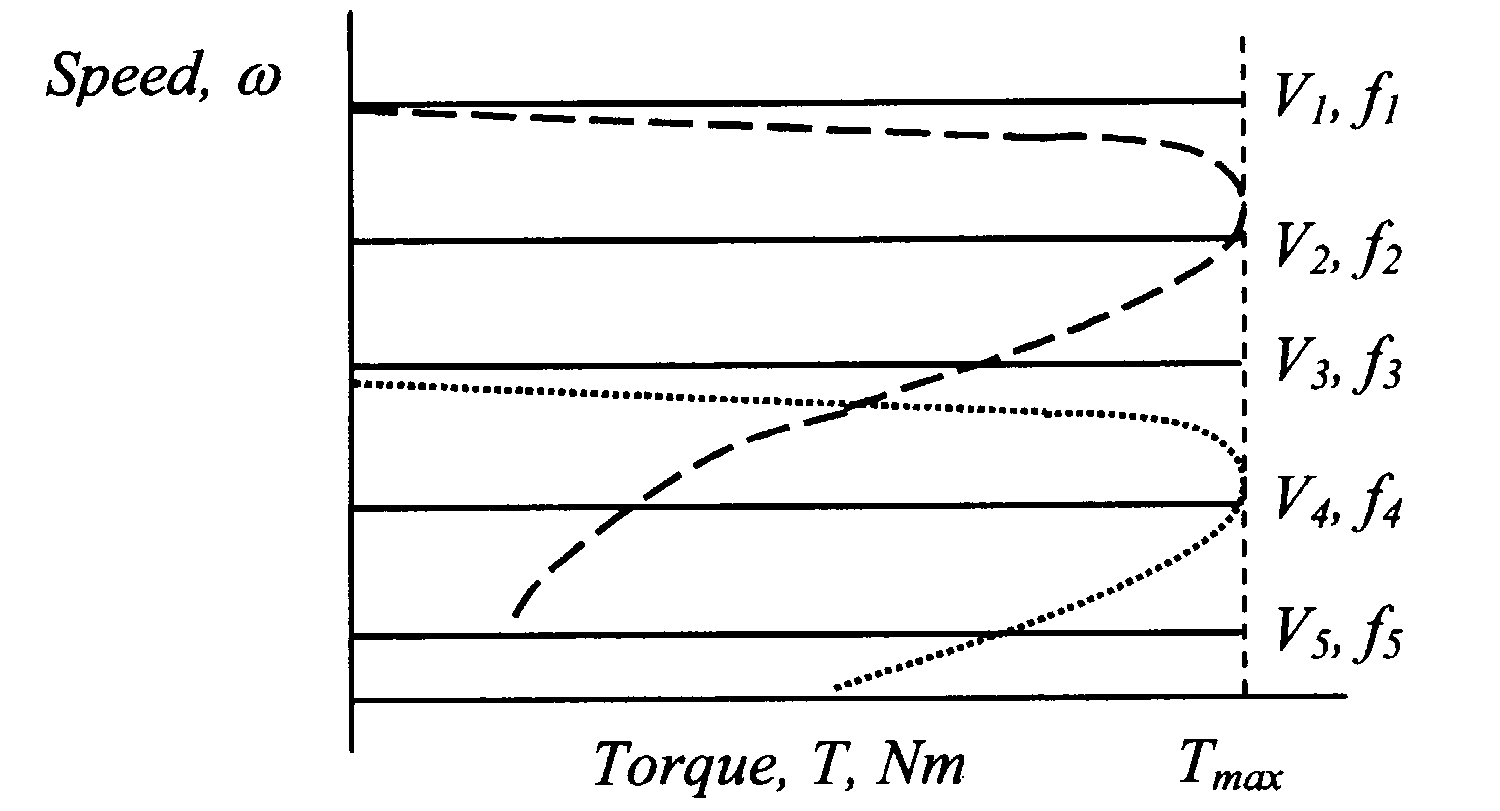
––Синхронный двигатель,
T-ω характеристика с постоянным соотношением V/f----Асинхронный двигатель,
T-ω характеристика при номинальной частоте····· Асинхронный двигатель
T-ω характеристика с постоянным соотношением V/f при ½ частоте от номинальной.Выражая частотную переменную
f1 как![]()
где
f0, является номинальной частотой (обычно 50Гц), уравнение крутящего момента 6.34 принимает вид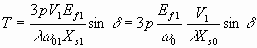 6.35
6.35
Пологая, что синусоидальное распределение потока ротора, связывает среднеквадратичное значение напряжения
Ef0, индуцируемого в статоре, действующего значения магнитной индукции ротора Br, частоты f0, и числа витков статора Ns следующим соотношениемEfo = 4.44f0NsBrA , где А – эффективная поверхность каждого полюса статора.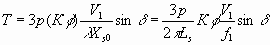 6.37
6.37
Из выражение 6.37 видно, что если соотношение
V/f остается постоянным, то крутящий момент, развивающийся при данном δ, такой же как и максимальный крутящий момент, который развивается во всем диапазоне скоростей. Заметьте, что этот результат основывается на допущении незначительного сопротивления статора..Заметьте, что приложение симметричного 3-х фазного синусоидального напряжения
V1 к обмоткам статора также ведет к появлению вращающегося поля согласно соотношению V1 = 4.44f1NsBsA 6.38где
Bs – действующее значение магнитной индукции статора при питании только статора. Развиваемый момент может также рассматриваться согласно тенденции совмещения полей статора и ротора Bs и Br соответственно.Из предыдущего исследования следует, что регулятор частоты вращения разомкнутого контура должен состоять из
V/f регулятора как обозначено на рисунке 6.19. Вводимое значение частоты f1, частоты источника питания двигателя выбирается согласно желаемой скорости и условию сохранения отношения входного напряжения f1 к частоте. Для этого может использоваться синусоидально-модулированный (SPWM) инвертор. Изменение задания на скорость должно быть таким, что бы ограничение δ(=90°) – никогда не превышалось. Для этой цели может использоваться фильтр в канале задания скорости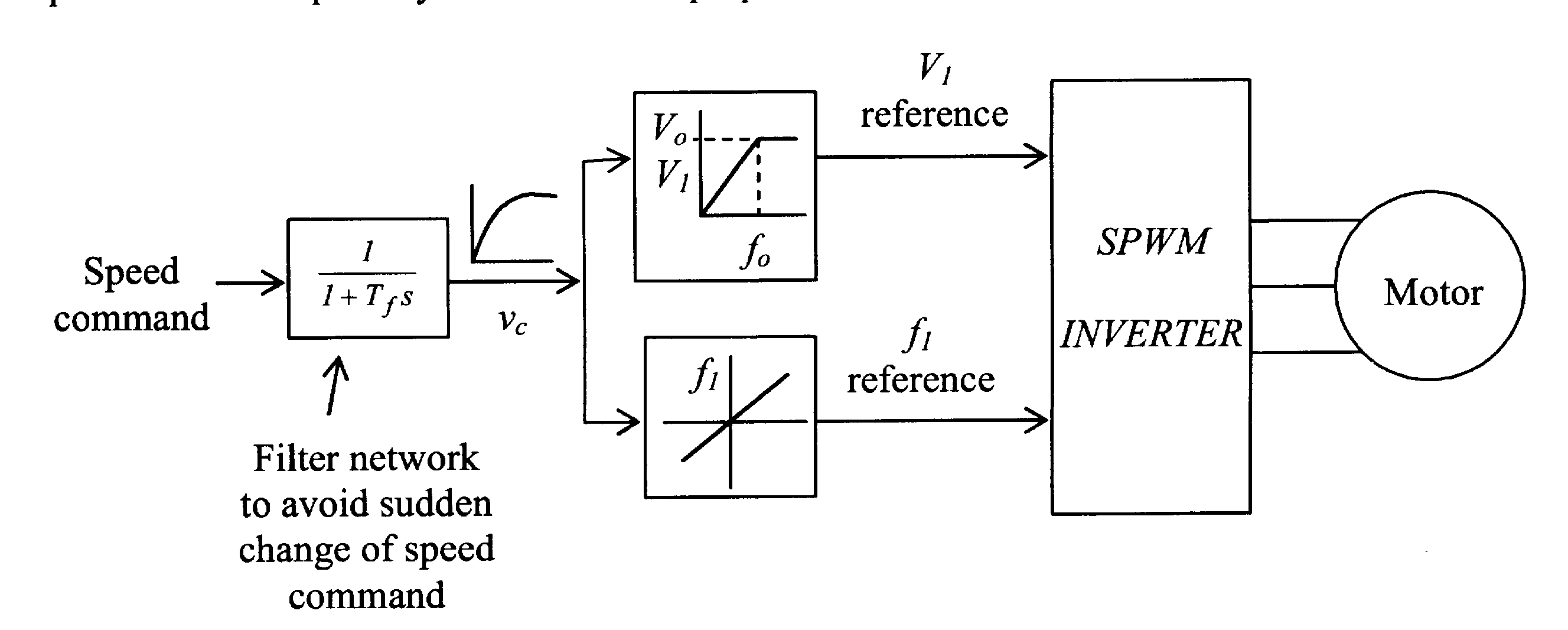
Обычно,
V1 возрастает пропорционально росту f1, до тех пор, пока номинальная частота(скорость) не будет достигнута. После этого, V1 поддерживается постоянным на уровне V0, которое является номинальным напряжением двигателя. Но для работы на скорости выше основной, увеличивают только частоту f1. Однако это, согласно уравнению 6.38, ослабляет потокосцепление статора.Когда доступен датчик установившегося положения вала, вектор потокосцепления ротора каждой фазы обмотки может быть разложен на фазу и амплитуду. (Есть также другие способы измерить угол
δ.). Максимальный угол между напряжениями статора V1a, Vlb, и V1c (то есть, δ1), и векторами потокосцепления ротора, для каждой фазы, может быть ограничен на уровне заданной величины. Максимальный развиваемый момент тогда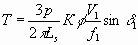 6.39
6.39
Механическая скорость, для любой частоты
f1 определяется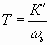 6.40
6.40
Обратимся к векторной диаграмме, показанной на рисунке ниже, в которой
R - не учитывается..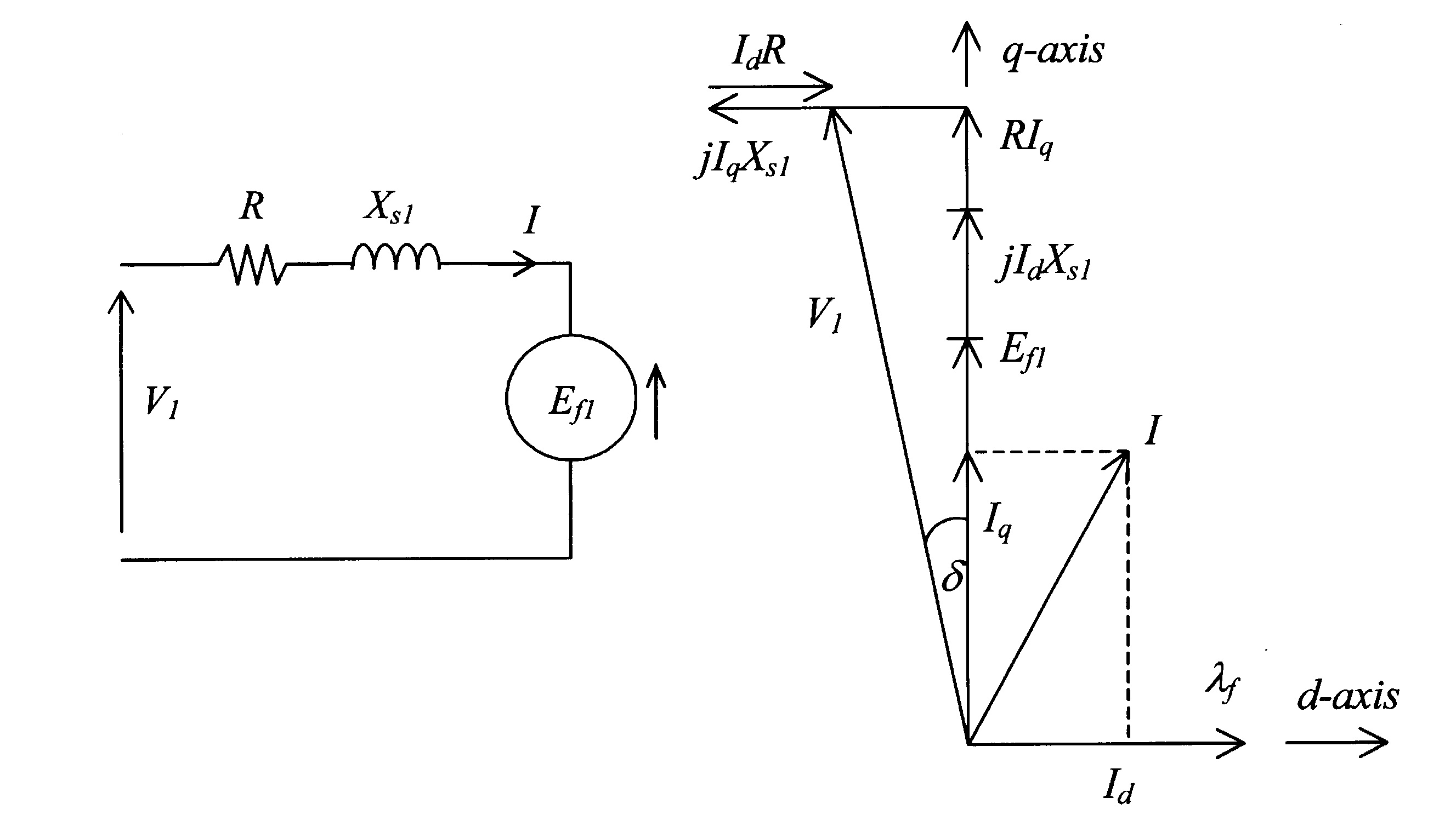
Из векторной диаграммы
![]() 6.41
6.41
![]() 6.42
6.42
Решая относительно
Id и Iq , из 6.41 и 6.42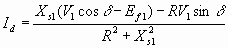 6.43
6.43
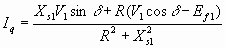 6.44
6.44
Развиваемая мощность составляет
![]() Watts/phase
Watts/phase
![]() Watts/phase
Watts/phase
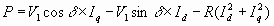 Watts/phase 6.45
Watts/phase 6.45
Полный развиваемый момент для всех трех фаз
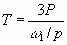 Nm
Nm
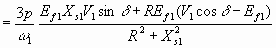 Nm 6.46
Nm 6.46
Выразим частоту
f1 через номинальную частоту f0, как![]()
итак
Ef1 = λEf0 = λe0V0, где![]()
где
Согласно уравнению 6.46 развиваемый момент
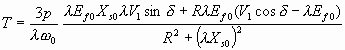
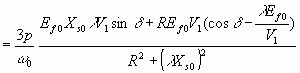 Nm 6.47
Nm 6.47
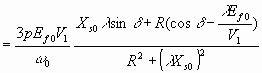 Nm 6.48
Nm 6.48
Дифференцируя числитель 6.48 относительно
δ и приравняв его к нулю, видно, что максимальный вращающий момент имеет место при δmax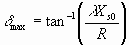 6.49
6.49
Используя это
δmax для λ, из уравнения 6.49, можно найти максимальный вращающий момент для любой скорости, согласно уравнению 6.48. Даже у привода с постоянным отношением V–f, максимальный момент, развиваемый двигателем, падает при низкой скорости из-за падения напряжения в сопротивлении статора. T–ω характеристика двигателя на рисунке 6.22 ясно демонстрирует, что снижение максимального момента двигателя, развиваемого при низких скоростях, когда сопротивление статора не незначительно.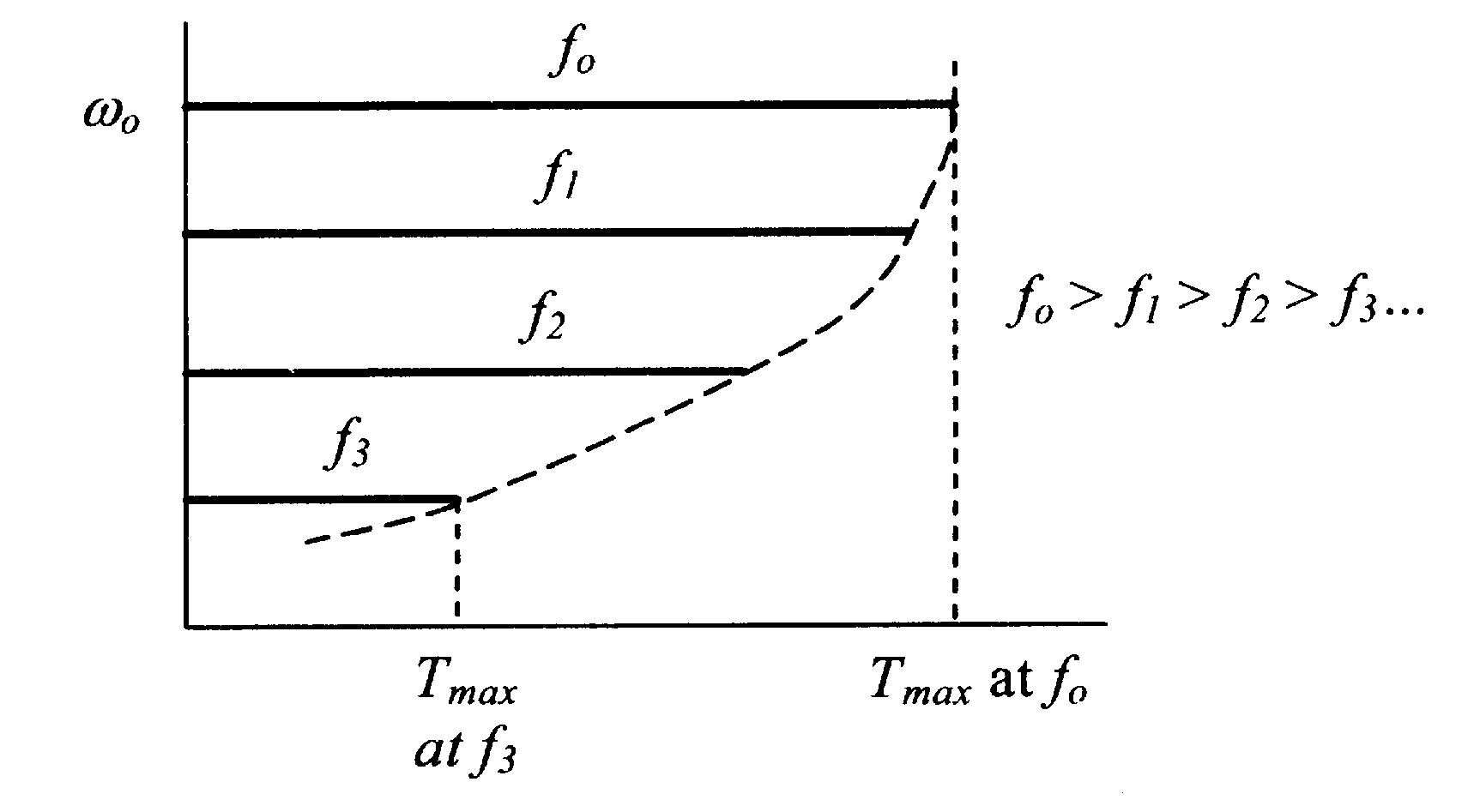
Заметьте, что в районе номинальной частоты,
λXSO>> R и R≈0, так, что уравнение вращающего момента 6.48 стало идентично 6.34.При низких частотах, где
λ ≈0, Xs1 и Efl незначительны. Из 6.41 и 6.42![]() 6.50
6.50
![]() 6.51
6.51
отсюда
Уравнение 6.52 подразумевает, что усиление разности потенциалов частоты нулевого порядка должно соответствовать
![]() 6.53
6.53
Из 6.48 развиваемый момент в области в низких частот
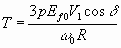 6.54
6.54
Следовательно, при низкой скорости,
Tmax достигается при δ= 0°Увеличение разности потенциалов при нулевой скорости (=
R x lrated) ведет к тому, что двигатель развивает полный расчетный вращающий момент при нулевой скорости. Увеличение разности потенциалов нужно постепенно понизить до нуля, поэтому при номинальной скорости, не применяется увеличение разности потенциалов.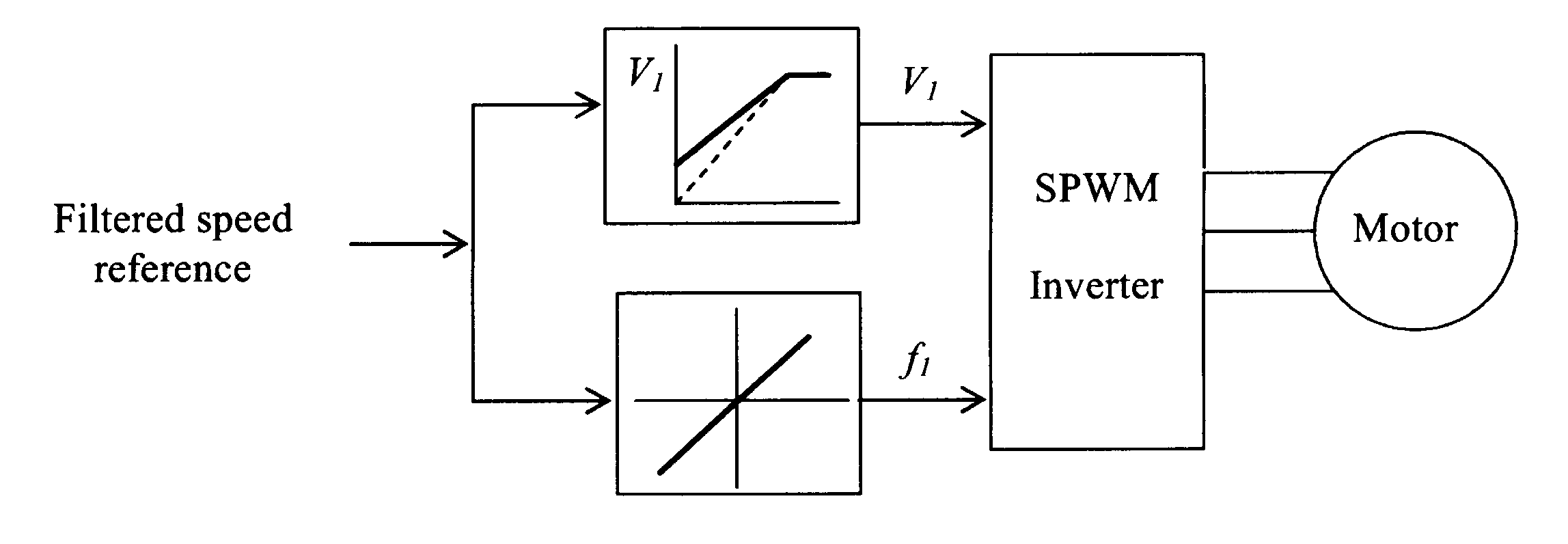
Пренебрегая сопротивлением статора
R, которое означает работу явнополюсного двигателя в области номинальной или повышенной частоты, развиваемый момент из уравнения 6.33,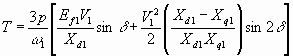 Nm 6.55
Nm 6.55
Как прежде, для любой заданной частоты
f1 = λf0,![]() ;
; ![]() ;
; ![]() ;
; ![]()
где нижний индекс
o обозначает номинальную частоту. Используя это, развиваемый момент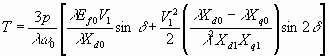 Nm 6.65
Nm 6.65
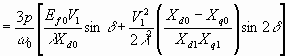 Nm 6.57
Nm 6.57
Таким образом, если
V1/f1 отношение сохраняется постоянным, тот же самый максимальный вращающий момент достигается для всех скоростей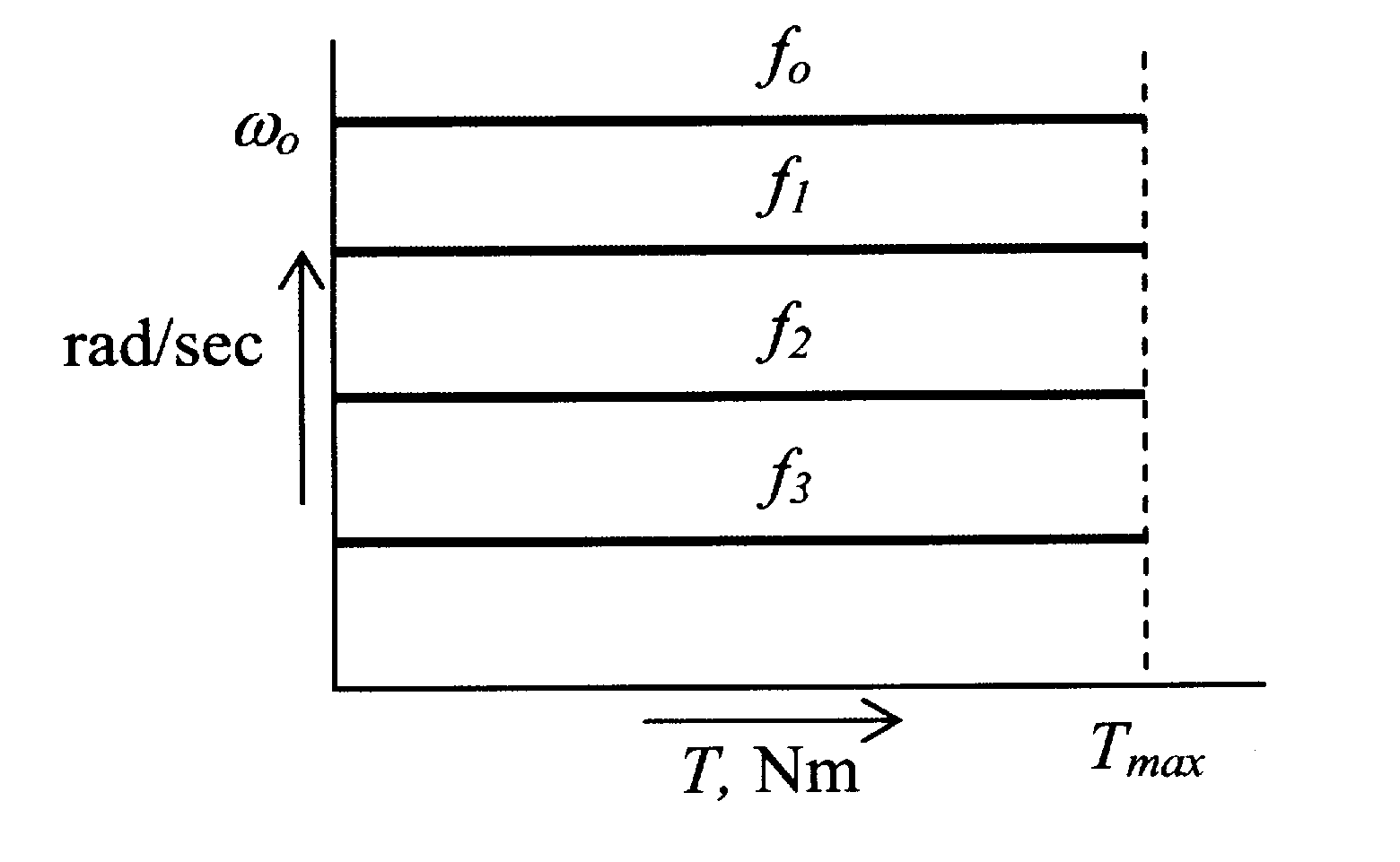
Разомкнутый регулятор скорости будет подобен изображенному на блок-схеме, расположенной на рисунке 6.19. Но с другой стороны, если угол нагрузки ограничен некоторым произвольным значением
δ1, и напряжение питания также остается постоянным, то расчетная величина V0, уравнения вращающего момента 6.57, имеет вид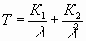 6.58
6.58
где
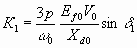 6.59
6.59
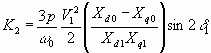 6.60
6.60
Уравнение 6.58 дает представление о постоянной мощности, как о
T–ω характеристике, подобной таковым из раздела 6.4.1.2 (рисунок 6.20).При низкой частоте, падение напряжения в сопротивлении статора может быть значительно. Обратимся к векторной диаграмме явнополюсного двигателя с
R≠0, как показано на рисунке ниже.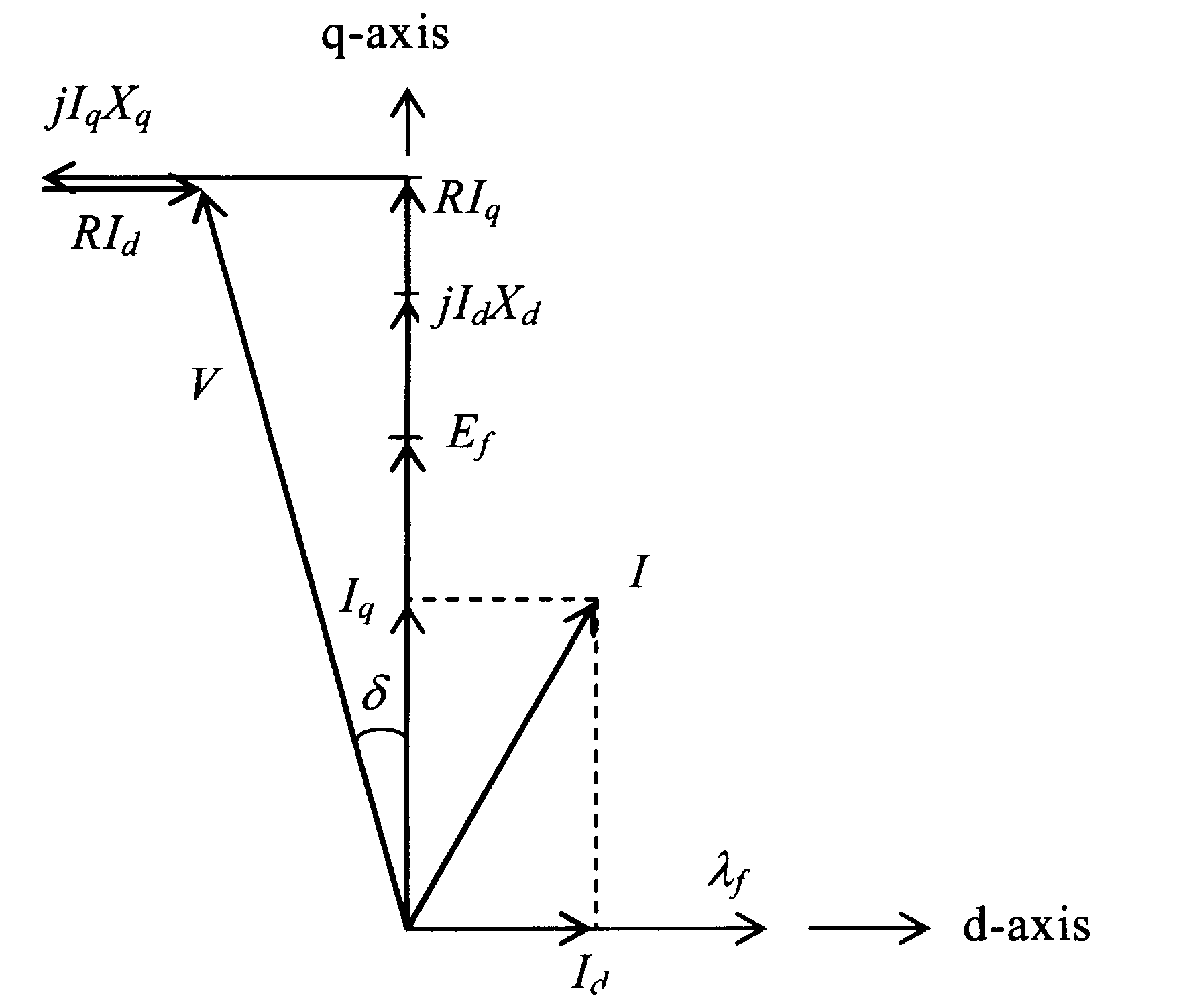
Из векторной диаграммы рисунок 6.25
![]() 6.61
6.61
![]() 6.62
6.62
Решая относительно
Id и Iq из 6.61 и 6.62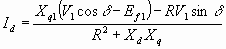 6.63
6.63
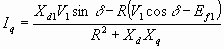 6.64
6.64
Развиваемая мощность
![]() Watts/phase
Watts/phase
![]() Watts/phase
Watts/phase
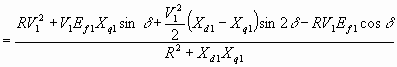 6.65
6.65
Обратите внимание при низкой скорости, где
λ ≈0, пока Xd, Xq, и Ef малы. Эти результаты ожидаемы и подразумевают, что нулево-частотное увеличение разности потенциалов имеет место при![]() 6.66
6.66
Напряжение статора частоты должно таким образом быть установлено при низкой частоте как обозначено уравнением 6.66. Согласно уравнению 6.53 это также имеет место для неявнополюсного двигателя.
.Развиваемый момент из 6.65
![]() Nm
Nm
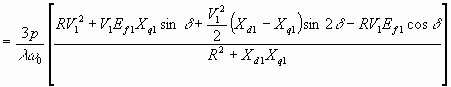 6.67
6.67
Для произвольной частоты источника питания
fl = λ f0, и входного напряжения V1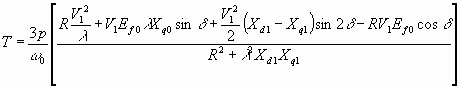 Nm 6.68
Nm 6.68
Из уравнения 6.68 видно, что максимальный вращающий момент, развиваемый двигателем, уменьшается по мере уменьшения частоты
(f1) или скорости, если сопротивление статора R значительно. Как прежде, условие (δmax), при котором возможно развитие максимального момента при любой частоте, может быть получено продифференцировав 6.68 и прировняв к нулю. Tmax находится подставляя δmax в уравнение 6.68. Выражение для δmax не приведено здесь ради краткости. T–ω характеристики для привода с постоянным соотношением V-f, для различных частот, будут подобны по форме показанным на рисунке 6.26.Способность двигателя развивать максимальный момент может быть поддержана, используя явление увеличения разности потенциалов в области низких частот и, уменьшая его некоторыми способами до нуля, как показано на блок-схеме фигуры рисунка 6.23
| <<< Предыдущая | Вернутся к Библиотеке |   |