Повернутися до бібліотеки
Вернуться в библиотеку
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРОЦЕССОВ В ШАХТНОЙ НИЗКОВОЛЬТНОЙ СЕТИ ПРИ ДУГОВОМ ЗАМЫКАНИИ
Математические методы в технике и технологиях — ММТТ-18.
Сб. трудов XVIII Международ. науч. конф.: В 10 т. Т. 5. Секция 5 / Под общ. ред. В.С.Балакирева.
— Казань: изд-во Казанского гос. технол. ун-та, 2005. — С.212-215.
Широкое применение гибких кабелей в низковольтной электросети шахт
обусловлено значительным количеством передвижных и переносных электропотребителей. Сложные условия
эксплуатации зачастую становятся причиной нарушения целостности изоляции таких кабелей и, как
следствие, возникновения короткого (к. з.), а также дугового (д. з.) замыкания [1].
Сопротивление электрической дуги, возникающей между фазами, носит активный характер, и
соразмерно с активным сопротивлением нагрузки. Поэтому д. з., оказывая негативное влияние на работу
электрооборудования и создавая опасность взрыва при наличии опасной концентрации метана в
рудничной атмосфере, как правило, не выявляется известными устройствами максимальной токовой защиты.
Поэтому актуальна задача исследования и, в частности, моделирования процессов, протекающих в
электротехническом комплексе участка шахты при возникновении д. з. в гибком кабеле.
Рассмотрим расчетную схему [1], состоящую из трансформаторной подстанции
(ТП), гибкого кабеля и электропотребителя (асинхронного двигателя — АД) (рис. 1).
Принятые обозначения: 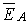 ,
,  ,
,
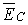 и
и  — ЭДС
вторичной обмотки ТП и ее импеданс;
— ЭДС
вторичной обмотки ТП и ее импеданс;  ,
,  —
полное сопротивление и длина участка кабеля от ТП до точки к. з.;
—
полное сопротивление и длина участка кабеля от ТП до точки к. з.; 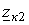 ,
,
 — то же от аварийной точки до АД.
— то же от аварийной точки до АД.

Рисунок 1 — Участковая сеть при дуговом замыкании
Возникновение и протекание д. з. характеризуется асимметрией токов и
напряжений. Их аналитический расчет целесообразно проводить методом симметричных составляющих [2].
Отсутствие нулевых составляющих в токах и напряжениях АД обусловлено применением сети с
изолированной нейтралью трансформатора и нагрузки. На рис. 2 приведены схемы замещения
рассматриваемой системы для прямой и обратной составляющих, соединенные в месте короткого
замыкания через переходное сопротивление 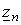 .
Приняты обозначения:
.
Приняты обозначения: 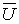 — вектор напряжения сети в
неповрежденной фазе А;
— вектор напряжения сети в
неповрежденной фазе А; 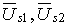 — составляющие напряжения
на зажимах статора;
— составляющие напряжения
на зажимах статора;  — составляющие тока в
статоре;
— составляющие тока в
статоре;  — импеданс АД для прямых составляющих токов;
— импеданс АД для прямых составляющих токов;
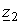 — импеданс машины, соответствующий скольжению
— импеданс машины, соответствующий скольжению 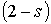 .
Величины
.
Величины  и
и 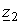 определяются из Т-образной схемы замещения асинхронной машины [3].
определяются из Т-образной схемы замещения асинхронной машины [3].
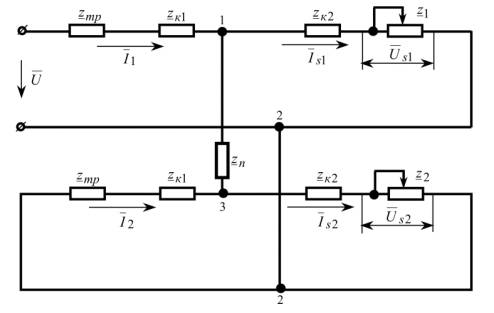
Рисунок 2 — Схемы замещения для прямой и
обратной последовательности, соединенные в месте к.з. через переходное сопротивление
Из схемы замещения следует определение составляющих токов и напряжений:
| |
 , ,  |
(1) |
| |
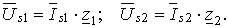 |
(2) |
где 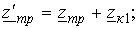
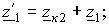
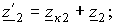
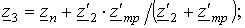
 .
.
Прямой и обратный порядок чередования фаз напряжения определяет наличие
вращающего 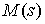 и тормозного
и тормозного  моментов АД [2].
Тогда общий статический момент, развиваемый двигателем, может быть определен из выражения:
моментов АД [2].
Тогда общий статический момент, развиваемый двигателем, может быть определен из выражения:
| |
 . . |
(3) |
Уравнения (1) — (3) позволяют построить искусственную механическую
характеристику АД, обусловленную асимметрией параметров питающей сети, откуда, с учетом
постоянства момента сопротивления нагрузки, может быть найдено соответствующее скольжение
двигателя 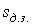 . Окончательный расчет по выражениям
(1) — (3) следует вести для
. Окончательный расчет по выражениям
(1) — (3) следует вести для 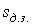 . Параметр, вычисленный
по (3), представляет собой лишь среднюю величину электромагнитного момента АД во времени.
Найдем выражение для пульсирующей с двойной частотой
. Параметр, вычисленный
по (3), представляет собой лишь среднюю величину электромагнитного момента АД во времени.
Найдем выражение для пульсирующей с двойной частотой 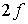 его динамической составляющей.
его динамической составляющей.
Вектор тока статора:
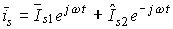 ,
,
где  - круговая частота тока статора, рад/с.
- круговая частота тока статора, рад/с.
Аналогично:
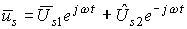 ,
,
Допустим, что в момент времени 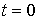 :
:
 ;
; 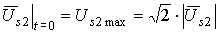 ;
;
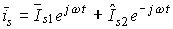 .
.
Полные проводимости двигателя прямого и обратного следования фаз:
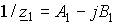 ;
; 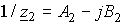 ,
,
где  ,
,  ,
, 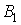 ,
,
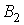 — соответственно действительные (
— соответственно действительные (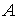 )
и мнимые (
)
и мнимые (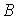 ) части проводимостей двигателя прямого и
обратного следования фаз.
) части проводимостей двигателя прямого и
обратного следования фаз.
Следовательно:
 ;
; 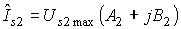 .
.
Для вектора тока статора имеем:
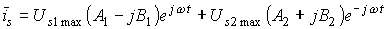 .
.
Пренебрегая активным сопротивлением статора, запишем выражение для
вектора потокосцепления:
 .
.
Электромагнитный момент АД с числом пар полюсов 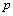 :
:
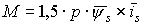 .
.
После преобразований получим:
| |
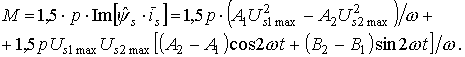 |
(4) |
Первое слагаемое в (4) есть среднее во времени значение вращающего
момента  , развиваемого двигателем в установившемся
аварийном режиме; второе слагаемое представляет собой момент
, развиваемого двигателем в установившемся
аварийном режиме; второе слагаемое представляет собой момент 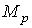 ,
пульсирующий с удвоенной частотой (рис. 3):
,
пульсирующий с удвоенной частотой (рис. 3):
 .
.
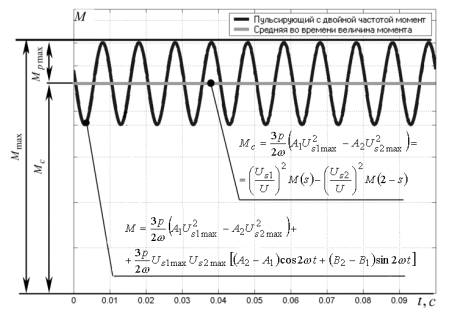
Рисунок 3 — График пульсирующего с
двойной частотой электромагнитного момента во временной области
Для характеристики пульсирующего момента введем показатель пульсаций:
| |
 , , |
(5) |
где  — максимальное значение момента за
период;
— максимальное значение момента за
период; 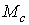 — среднее во времени значение вращающего
момента;
— среднее во времени значение вращающего
момента; 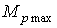 — амплитуда пульсирующей составляющей.
— амплитуда пульсирующей составляющей.
С целью определения 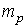 через
известные параметры схемы замещения, выразим амплитуду пульсирующей составляющей:
через
известные параметры схемы замещения, выразим амплитуду пульсирующей составляющей:

Тогда можно записать
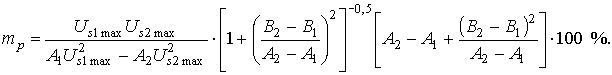
На рис. 4 представлены зависимости показателя пульсаций от местоположения
точки д. з. и активного сопротивления дуги.
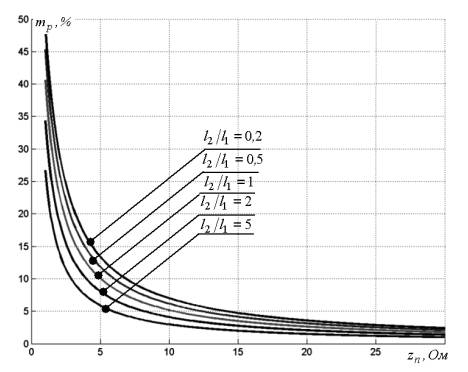
Рисунок 4 — Показатель пульсаций
в функции от параметров точки д. з.
Таким образом, в результате моделирования уточнено состояние
асинхронного двигателя в случае возникновения дугового замыкания в сети электропитания.
Полученные аналитические зависимости позволяют выявить особенности влияния на его токи,
напряжения статора и вращающий момент таких параметров процесса дугового замыкания,
как место повреждения междуфазной изоляции кабельной линии (учитывается сопротивлением
участков кабеля до и после точки замыкания) и сопротивление электрической дуги.
Перечень ссылок
- Риман Я.С. Защита шахтных участковых сетей от токов короткого замыкания. 2-е изд., перераб.
и доп. — М.: Недра, 1985. — 88 с.
- Ковач К.П., Рац. И. Переходные процессы в машинах переменного тока. — М.-Л.: Госэнергоиздат, 1963. — 744 с.
- Копылов И.П. Электрические машины. Учебник для вузов. 4-е изд. — М.: Высшая школа, 2004. — 607 с.
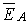 ,
,  ,
,
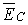 и
и  — ЭДС
вторичной обмотки ТП и ее импеданс;
— ЭДС
вторичной обмотки ТП и ее импеданс;  ,
,  —
полное сопротивление и длина участка кабеля от ТП до точки к. з.;
—
полное сопротивление и длина участка кабеля от ТП до точки к. з.; 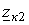 ,
,
 — то же от аварийной точки до АД.
— то же от аварийной точки до АД.
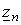 .
Приняты обозначения:
.
Приняты обозначения: 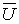 — вектор напряжения сети в
неповрежденной фазе А;
— вектор напряжения сети в
неповрежденной фазе А; 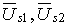 — составляющие напряжения
на зажимах статора;
— составляющие напряжения
на зажимах статора;  — составляющие тока в
статоре;
— составляющие тока в
статоре;  — импеданс АД для прямых составляющих токов;
— импеданс АД для прямых составляющих токов;
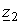 — импеданс машины, соответствующий скольжению
— импеданс машины, соответствующий скольжению 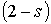 .
Величины
.
Величины 
 ,
, 
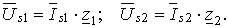
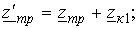
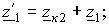
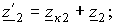
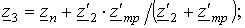
 .
.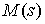 и тормозного
и тормозного  моментов АД [2].
Тогда общий статический момент, развиваемый двигателем, может быть определен из выражения:
моментов АД [2].
Тогда общий статический момент, развиваемый двигателем, может быть определен из выражения: .
.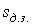 . Окончательный расчет по выражениям
(1) — (3) следует вести для
. Окончательный расчет по выражениям
(1) — (3) следует вести для 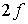 его динамической составляющей.
его динамической составляющей.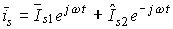 ,
, - круговая частота тока статора, рад/с.
- круговая частота тока статора, рад/с.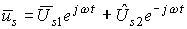 ,
,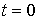 :
:
 ;
; 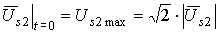 ;
;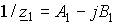 ;
; 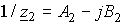 ,
, ,
,  ,
, 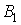 ,
,
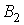 — соответственно действительные (
— соответственно действительные (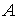 )
и мнимые (
)
и мнимые (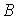 ) части проводимостей двигателя прямого и
обратного следования фаз.
) части проводимостей двигателя прямого и
обратного следования фаз. ;
; 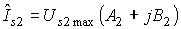 .
.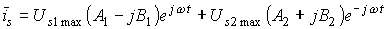 .
. .
.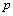 :
: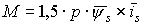 .
.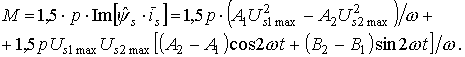
 , развиваемого двигателем в установившемся
аварийном режиме; второе слагаемое представляет собой момент
, развиваемого двигателем в установившемся
аварийном режиме; второе слагаемое представляет собой момент 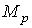 ,
пульсирующий с удвоенной частотой (рис. 3):
,
пульсирующий с удвоенной частотой (рис. 3): .
.
 ,
, — максимальное значение момента за
период;
— максимальное значение момента за
период; 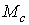 — среднее во времени значение вращающего
момента;
— среднее во времени значение вращающего
момента; 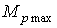 — амплитуда пульсирующей составляющей.
— амплитуда пульсирующей составляющей.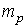 через
известные параметры схемы замещения, выразим амплитуду пульсирующей составляющей:
через
известные параметры схемы замещения, выразим амплитуду пульсирующей составляющей: