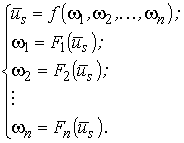Повернутися до бібліотеки
Вернуться в библиотеку
УДК 621.647.1
(Украина, Донецк, Донецкий национальный технический университет)
ИССЛЕДОВАНИЕ ПРОЦЕССОВ В УЧАСТКОВОЙ ЭЛЕКТРОСЕТИ ПРИ ГРУППОВОМ ВЫБЕГЕ АСИНХРОННЫХ ДВИГАТЕЛЕЙ
Гірнича електромеханіка та автоматика: Наук.-техн. зб. — 2005. — Вип. 74. — С. 30-36.
Постановка проблемы и ее связь с прикладными задачами
Автоматическое защитное отключение шахтной участковой электросети,
содержащей асинхронные двигатели (АД) потребителей, не может обеспечить мгновенное её
обесточивание, а следовательно, не достаточно для обеспечения безопасности эксплуатации последней.
После отключения напряжения в питающей сети роторы двигателей продолжают вращаться по инерции,
генерируя в сеть ЭДС вращения. Последняя, во-первых, поддерживает во включенном состоянии
контакторы пускателей, во-вторых, подпитывает аварийную точку участковой сети, что создаёт
предпосылки развития аварийной ситуации.
Исследование процессов в участковой сети при одновременном выбеге
нескольких двигателей (что, как правило, имеет место на практике), представляется актуальным,
поскольку позволит получить более точное представление о факторах поддержания аварийного состояния
электросети и в дальнейшем обосновать структуру и параметры эффективных средств подавления ЭДС
вращения группы асинхронных двигателей в режиме свободного выбега при аварийном отключении
напряжения на участке шахты.
Анализ исследований и публикаций
Математическое описание процессов, происходящих при одновременном
отключении как одного, так и группы двигателей, приводится в [1], однако при этом не учитывается
изменение скорости вращения роторов АД различных типов и мощности с течением времени, что является
существенным фактором. В [2, 3] указывается негативное влияние ЭДС вращения двигателя на
электробезопасность эксплуатации участковых электросетей, однако не исследован процесс группового
выбега двигателей потребителей с позиций воздействия на цепь утечки тока на землю в электросети.
Он требует дополнительного изучения.
Постановка задачи
Задачей данных исследований является обоснование параметров математической
модели, позволяющей установить характер изменения напряжения в низковольтной трехфазной
электрической сети при её отключении, обусловленного совместным действием ЭДС вращения АД разной
мощности в режиме выбега.
Основной материал и результаты исследований
Рассмотрению подлежит система, состоящая из  АД, включенных на общую сеть
(рис. 1). При обосновании математической модели процесса реальные многополюсные двигатели
представлены эквивалентными двухполюсными машинами. Параметры гибких кабелей не учитываются.
До момента времени
АД, включенных на общую сеть
(рис. 1). При обосновании математической модели процесса реальные многополюсные двигатели
представлены эквивалентными двухполюсными машинами. Параметры гибких кабелей не учитываются.
До момента времени  защитного отключения сети
автоматическим выключателем (АВ) все двигатели работали в номинальном режиме, электромагнитные и
электромеханические переходные процессы в электросети и электроприводах завершены. При этом на
двигатели потребителей участка подавалось напряжение сети, мгновенное значение которого для
каждой фазы равно:
защитного отключения сети
автоматическим выключателем (АВ) все двигатели работали в номинальном режиме, электромагнитные и
электромеханические переходные процессы в электросети и электроприводах завершены. При этом на
двигатели потребителей участка подавалось напряжение сети, мгновенное значение которого для
каждой фазы равно:
| |
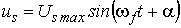 , , |
(1) |
где  — круговая частота напряжения сети.
— круговая частота напряжения сети.
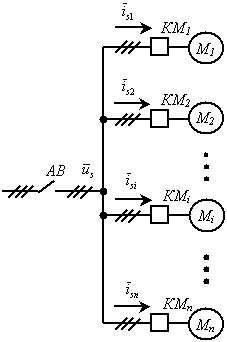
Рис. 1. Схема электромеханического комплекса
участка шахты
При условии отключения в момент времени  контакторов КМ1—КМn напряжения на зажимах отдельных АД (рис. 2)
определяются параметрами и условиями выбега каждого отдельного двигателя [1].
контакторов КМ1—КМn напряжения на зажимах отдельных АД (рис. 2)
определяются параметрами и условиями выбега каждого отдельного двигателя [1].
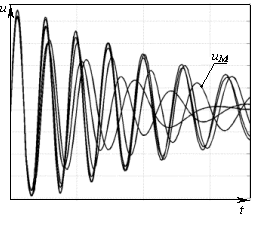
Рис. 2. Диаграммы ЭДС вращения двигателей
разомкнутой сети
Однако реально после отключения АВ контакторы КМ1—КМn
пускателей остаются во включенном состоянии, что обусловливает электрическую связь находящихся в
режиме выбега двигателей М1—Мn. При этом имеет место
принудительное уравнивание напряжений на зажимах всех АД, вследствие чего между отдельными
двигателями протекают уравнительные токи, алгебраическая сумма которых равна нулю.
Результирующий вектор напряжения в сети:
| |
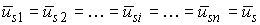 . . |
(2) |
Известно, что оператор Лапласа 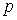 ,
характеризующий изменение напряжения в сети в режиме группового выбега двигателей, может быть
определен из выражения [1]:
,
характеризующий изменение напряжения в сети в режиме группового выбега двигателей, может быть
определен из выражения [1]:
| |
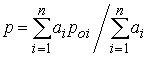 , , |
(2) |
где  — коэффициент, определяемый из соотношения:
— коэффициент, определяемый из соотношения:
| |
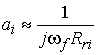 , , |
(4) |
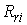 — сопротивление ротора i-го двигателя,
приведенное к статору.
— сопротивление ротора i-го двигателя,
приведенное к статору.
Величина  характеризует затухание
тока в роторе i-го двигателя:
характеризует затухание
тока в роторе i-го двигателя:
| |
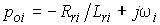 , , |
(5) |
где 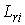 — полная индуктивность ротора i-го двигателя;
— полная индуктивность ротора i-го двигателя;
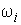 — частота вращения ротора i-го двигателя.
— частота вращения ротора i-го двигателя.
Тогда в отношении 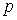 справедливо выражение:
справедливо выражение:
| |
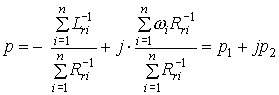 , , |
(6) |
где 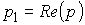 ,
, 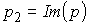 .
.
Таким образом, переменное напряжение в участковой сети при групповом
выбеге АД характеризуется постоянной времени  и скоростью
изменения
и скоростью
изменения 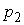 . Поскольку
. Поскольку  ,
а частоты вращения роторов с течением времени изменяются, то
,
а частоты вращения роторов с течением времени изменяются, то 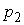 —
функция времени:
—
функция времени:  . Следовательно,
. Следовательно, 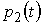 является модулирующим сигналом для частоты колебаний напряжения
является модулирующим сигналом для частоты колебаний напряжения 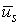 .
.
Вектор напряжения, амплитуда которого уменьшается по экспоненциальному
закону, учитывая частотную модуляцию, определяется соотношением:
| |
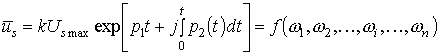 , , |
(7) |
где  — коэффициент, равный 0,83 при номинальной
нагрузке, 0,95 при холостом ходе [3].
— коэффициент, равный 0,83 при номинальной
нагрузке, 0,95 при холостом ходе [3].
Из (7) следует, что вектор 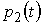 определяется, помимо параметров схем замещения АД, частотами вращения роторов при выбеге. При
определении
определяется, помимо параметров схем замещения АД, частотами вращения роторов при выбеге. При
определении  необходимо учитывать, что уравнительные
токи
необходимо учитывать, что уравнительные
токи 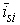 , протекающие в статорных обмотках двигателей при
совместном выбеге, обусловливают наличие электромагнитных моментов в машинах, что влияет на
интенсивность замедления роторов во времени. В зависимости от направления вектора тока данные
моменты в разных машинах могут иметь различный знак, соответствующий двигательному или
генераторному режиму конкретного двигателя.
, протекающие в статорных обмотках двигателей при
совместном выбеге, обусловливают наличие электромагнитных моментов в машинах, что влияет на
интенсивность замедления роторов во времени. В зависимости от направления вектора тока данные
моменты в разных машинах могут иметь различный знак, соответствующий двигательному или
генераторному режиму конкретного двигателя.
Для математического моделирования переходного процесса, имеющего место
при групповом выбеге АД, необходимо составить систему уравнений, в которую, помимо (7),
должны войти уравнения для каждого из 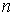 двигателей.
двигателей.
Необходимые соотношения могут быть определены из анализа схемы замещения
асинхронной машины в переходных процессах (рис. 3) [1]. Уравнения процессов в неподвижной системе
координат 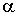
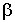 (
( ) для АД с короткозамкнутым ротором (
) для АД с короткозамкнутым ротором (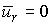 ),
учитывая скольжение
),
учитывая скольжение 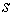 (обозначения переменных приняты
согласно [1]) — следующие:
(обозначения переменных приняты
согласно [1]) — следующие:
| |
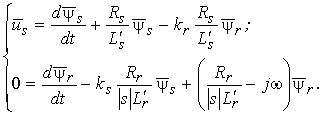 |
(8) |

Рис. 3. Схема замещения асинхронной машины в переходных режимах
Уравнения моментов АД представляются соотношениями:
| |
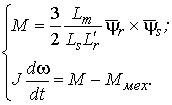 |
(9) |
Скольжение двигателя, электрически связанного с другими АД, в режиме
выбега определяется выражением:
| |
 . . |
(10) |
Раскладывая векторы по осям  и
и
 :
:
полагая
и приводя уравнения к явной форме Коши с учетом (9), можно записать:
| |
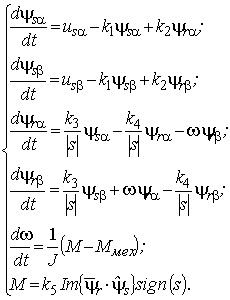 |
(13) |
Система уравнений (13) связывает скорость вращения двигателя
 с вектором напряжения на статоре
с вектором напряжения на статоре 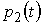 при свободном выбеге. В общем случае для i-го двигателя решение системы (13) выражается
в виде функциональной зависимости:
при свободном выбеге. В общем случае для i-го двигателя решение системы (13) выражается
в виде функциональной зависимости:
| |
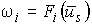 . . |
(14) |
Для анализа одновременного выбега 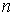 двигателей необходимо составить обобщенную систему уравнений, включающую зависимость (14)
для каждого двигателя, подключенного к общей сети, и уравнение (7), связывающее вектор
напряжения в сети со скоростями вращения роторов всех двигателей:
двигателей необходимо составить обобщенную систему уравнений, включающую зависимость (14)
для каждого двигателя, подключенного к общей сети, и уравнение (7), связывающее вектор
напряжения в сети со скоростями вращения роторов всех двигателей:
| |
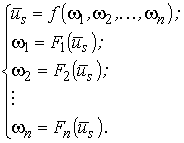 |
(15) |
При заданных начальных условиях система (15) может быть решена численными
методами с использованием средств вычислительной техники.
В частности, для случая одновременного выбега двух номинально нагруженных
двигателей мощностью 200 кВт и 30 кВт соответственно система (15) была решена численным методом
для временного интервала 0 — 0,2с (рис. 4).

Рис. 4. Расчетная диаграмма изменения напряжения в сети
при выбеге двух АД мощностью 200 кВт и 30 кВт
Анализ полученных аналитических зависимостей, а также сравнение диаграмм
изменения напряжений на зажимах двигателей при независимом (рис. 2) и групповом (рис. 4) выбеге
АД позволили установить следующее. При независимом выбеге (все контакторы КМ отключены)
напряжения на зажимах каждого двигателя определяются лишь параметрами схемы замещения и условиями
выбега каждого АД в отдельности. В режиме группового выбега (АВ отключен, все контакторы КМ
включены) напряжение в общей части электрической сети определяется совокупностью свойств и
параметров состояния всех АД и может быть определено вследствие решения системы (15).
Выводы и направления дальнейших исследований
Обобщенная математическая модель позволяет установить характер изменения
напряжения, обусловленного совокупным действием ЭДС вращения нескольких АД, находящихся в режиме
выбега, в низковольтной электрической сети.
С целью повышения точности результатов моделирования в ходе дальнейших
исследований целесообразно учесть параметры гибких кабелей, соединяющих элементы рассматриваемой
электротехнической системы.
Список литературы
- Ковач К.П., Рац. И. Переходные процессы в машинах переменного тока. — М.-Л.:
Госэнергоиздат, 1963. — 744 с.
- Дзюбан В.С. Аппараты защиты от токов утечки в шахтных электрических сетях.
— М.: Недра, 1982. — 152 с.
- Риман Я.С. Защита подземных электрических установок угольных шахт. — М.: Недра,
1977. — 206 с.
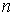 АД, включенных на общую сеть
(рис. 1). При обосновании математической модели процесса реальные многополюсные двигатели
представлены эквивалентными двухполюсными машинами. Параметры гибких кабелей не учитываются.
До момента времени
АД, включенных на общую сеть
(рис. 1). При обосновании математической модели процесса реальные многополюсные двигатели
представлены эквивалентными двухполюсными машинами. Параметры гибких кабелей не учитываются.
До момента времени 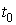 защитного отключения сети
автоматическим выключателем (АВ) все двигатели работали в номинальном режиме, электромагнитные и
электромеханические переходные процессы в электросети и электроприводах завершены. При этом на
двигатели потребителей участка подавалось напряжение сети, мгновенное значение которого для
каждой фазы равно:
защитного отключения сети
автоматическим выключателем (АВ) все двигатели работали в номинальном режиме, электромагнитные и
электромеханические переходные процессы в электросети и электроприводах завершены. При этом на
двигатели потребителей участка подавалось напряжение сети, мгновенное значение которого для
каждой фазы равно: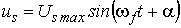 ,
, — круговая частота напряжения сети.
— круговая частота напряжения сети.

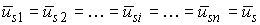 .
.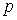 ,
характеризующий изменение напряжения в сети в режиме группового выбега двигателей, может быть
определен из выражения [1]:
,
характеризующий изменение напряжения в сети в режиме группового выбега двигателей, может быть
определен из выражения [1]: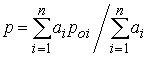 ,
, — коэффициент, определяемый из соотношения:
— коэффициент, определяемый из соотношения:
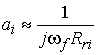 ,
,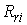 — сопротивление ротора i-го двигателя,
приведенное к статору.
— сопротивление ротора i-го двигателя,
приведенное к статору. характеризует затухание
тока в роторе i-го двигателя:
характеризует затухание
тока в роторе i-го двигателя: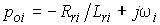 ,
,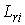 — полная индуктивность ротора i-го двигателя;
— полная индуктивность ротора i-го двигателя;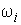 — частота вращения ротора i-го двигателя.
— частота вращения ротора i-го двигателя.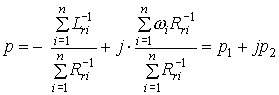 ,
,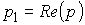 ,
, 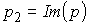 .
. и скоростью
изменения
и скоростью
изменения 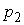 . Поскольку
. Поскольку  ,
а частоты вращения роторов с течением времени изменяются, то
,
а частоты вращения роторов с течением времени изменяются, то  . Следовательно,
. Следовательно, 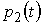 является модулирующим сигналом для частоты колебаний напряжения
является модулирующим сигналом для частоты колебаний напряжения 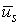 .
.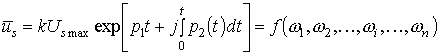 ,
, — коэффициент, равный 0,83 при номинальной
нагрузке, 0,95 при холостом ходе [3].
— коэффициент, равный 0,83 при номинальной
нагрузке, 0,95 при холостом ходе [3]. необходимо учитывать, что уравнительные
токи
необходимо учитывать, что уравнительные
токи 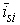 , протекающие в статорных обмотках двигателей при
совместном выбеге, обусловливают наличие электромагнитных моментов в машинах, что влияет на
интенсивность замедления роторов во времени. В зависимости от направления вектора тока данные
моменты в разных машинах могут иметь различный знак, соответствующий двигательному или
генераторному режиму конкретного двигателя.
, протекающие в статорных обмотках двигателей при
совместном выбеге, обусловливают наличие электромагнитных моментов в машинах, что влияет на
интенсивность замедления роторов во времени. В зависимости от направления вектора тока данные
моменты в разных машинах могут иметь различный знак, соответствующий двигательному или
генераторному режиму конкретного двигателя.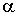
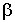 (
( ) для АД с короткозамкнутым ротором (
) для АД с короткозамкнутым ротором (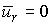 ),
учитывая скольжение
),
учитывая скольжение 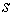 (обозначения переменных приняты
согласно [1]) — следующие:
(обозначения переменных приняты
согласно [1]) — следующие: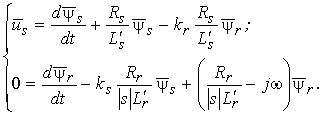

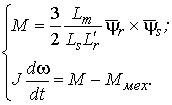
 .
.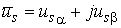 ,
,
 ,
,
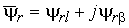 ,
, ,
,
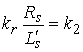 ,
,
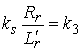 ,
,
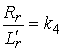 ,
,
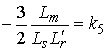 ,
,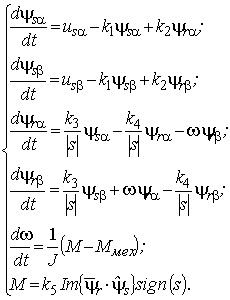
 с вектором напряжения на статоре
с вектором напряжения на статоре 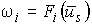 .
.