Повернутися до бібліотеки
Вернуться в библиотеку
УДК 621.647.1
МАТЕМАТИЧНЕ МОДЕЛЮВАННЯ ГРУПОВОГО ВИБІГУ ЕЛЕКТРОДВИГУНІВ СПОЖИВАЧІВ ТЕХНОЛОГІЧНОЇ
ДІЛЬНИЦІ ШАХТИ
Наукові праці Донецького національного технічного університету.
Серія “Гірнично-електромеханічна”. Випуск 101. — Донецьк: ДонНТУ, 2005. — С.103-110
Складена та проаналізована математична модель електротехнічного комплексу дільниці шахти під
час групового вибігу асинхронних двигунів після захисного відключення.
The mathematical model of the mines local electrotechnical system during a free movement of
asynchronous engines after its switching-off was made up and analysed.
Актуальність проблеми та її зв'язок з прикладними задачами
Електротехнічний комплекс дільниці вугільної шахти являє собою сукупність
асинхронних двигунів (АД) споживачів, кабельних ліній та комутаційної апаратури. Специфічні
умови експлуатації підземного електрообладнання та кабелів є причиною частих аварій, які
призводять до ураження людей електричним струмом, пожеж та вибухів [1,2]. З метою забезпечення
високого рівня безепеки підземних електроустановок використовуються різноманітні пристрої
автоматичного захисту [1], які забезпечують відключення мережі за визначений Правилами безпеки
час. Однак, характерною рисою АД є генерування ЕРС обертаня впродовж деякого часу після
відключення [1, 3], що негативно впливає на забезпечення електробезпеки у разі виникнення
аварійної ситуації.
У зв'язку з цим актуальним є дослідження процесів у електротехнічному
комплексі дільниці шахти під час групового вибігу АД споживачів після захисного відключення
мережі, оскільки це дозволить обґрунтувати вимоги та структуру перспективного автоматичного
захисту від негативного впливу ЕРС обертання на аварійну точку електромережі.
Аналіз досліджень та публікацій
Загальний підхід до математичного описання групового вибігу АД викладений
в [3], однак наведені залежності не враховують, по-перше, зміну швидкості обертання роторів АД з
часом, по-друге, наявність кабельних ліній, що з'єднують елементи електромережі. В [1]
вказується негативний вплив ЕРС обертання двигунів на дотримання параметрів електробезпеки
під час виникнення аварійних ситуацій.
Постановка задачі
Задачею досліджень є обґрунтування математичної моделі, що описує
процеси в електротехнічному комплексі технологічної дільниці шахти під час групового вибігу АД
споживачів різної потужності.
Основний матеріал та результати досліджень
Схема електромеханічного комплексу дільниці шахти під час
групового вибігу АД наведена на рис. 1. Прийняті наступні позначення: АВ - автоматичний вимикач;
КМ1,...,КМn - контактори магнітних пускачів; ГК1,...,ГКn - гнучкі кабелі. На рис. 1 також
вказані такі просторові вектори: 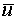 — напруги у
загальній частині мережі;
— напруги у
загальній частині мережі; 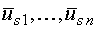 — напруги на затискачах
двигунів М1,...,Мn відповідно;
— напруги на затискачах
двигунів М1,...,Мn відповідно; 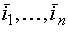 —
зрівнювальні струми у ланцюгах АД споживачів.
—
зрівнювальні струми у ланцюгах АД споживачів.
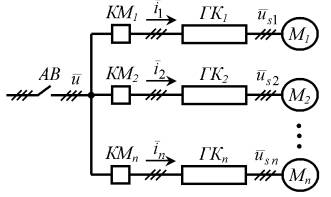
Рис. 1. Схема електромеханічного комплексу дільниці шахти
під час групового вибігу АД
На рис. 2 наведена схема заміщення ланцюга і-го споживача. На цій
схемі, окрім загальноприйнятих позначень Т-подібної схеми заміщення АД, 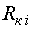 ,
,
 позначають активний опір та індуктивність фази гнучного
кабеля ГКі довжиною
позначають активний опір та індуктивність фази гнучного
кабеля ГКі довжиною 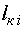 . Усі подальші
розрахунки здійснюватимуться у системі координат статора асинхронного двигуна (
. Усі подальші
розрахунки здійснюватимуться у системі координат статора асинхронного двигуна ( ) та для еквівалентних
двополюсних машин.
) та для еквівалентних
двополюсних машин.
Диференційне рівняння, що описує перехідні процеси у гнучкому кабелі,
згідно позначень схеми заміщення (рис. 2) має вигляд:
| |
 . . |
(1) |

Рис. 2. Схема заміщення ланцюга і-го
споживача
Переходячи до потокозчеплення  та
вводячи коефіцієнт затухання
та
вводячи коефіцієнт затухання 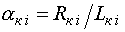 в операторній формі матимемо:
в операторній формі матимемо:
| |
 . . |
(2) |
Вектор струму 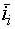 зв'язан з
потокозчепленнями АД виразом:
зв'язан з
потокозчепленнями АД виразом:
| |
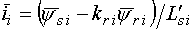 . . |
(3) |
Для потокозчеплення 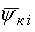 виконується співвідношення:
виконується співвідношення:
| |
 . . |
(4) |
Приймаються наступні позначення:
| |
 |
(5) |
де  ,
, 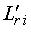 ,
,  ,
,
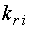 — перехідні індуктивності та коефіцієнти зв'язку
відповідно статора і ротора і-го двигуна.
— перехідні індуктивності та коефіцієнти зв'язку
відповідно статора і ротора і-го двигуна.
Переходячи до зображень за Лапласом, для схеми заміщення АД, враховуючи
(2), (4) і (5), запишемо відомі рівняня [3] в координатах 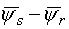 :
:
| |
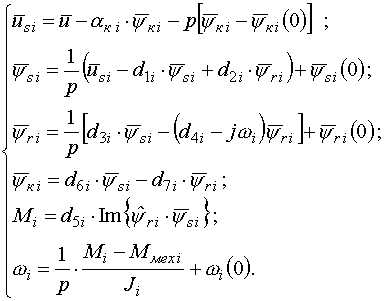 |
(6) |
Отримана система (6) являє собою математичну модель ланцюга і-го АД
з урахуванням параметрів відповідного гнучкого кабеля. Структурна схема моделі, що відповідає
цій системі рівнянь, наведена на рис. 3. Сукупність таких моделей для всіх n споживачів
буде використана при моделюванні перехідного процесу в електромеханічній системі дільниці, що
пов'язаний із вимкненням АВ.

Рис. 3. Структурна схема моделі
“ГК — АД”: а) розгорнутий вигляд; б) єдиним блоком
Припустимо, що до моменту  двигуни
М1,...,Мn споживачів були ввімкнені. У момент
двигуни
М1,...,Мn споживачів були ввімкнені. У момент  зникає живляча напруга й М1,...,Мn переходять до режиму групового
вибігу, який триває до відключення контакторів магнітних пускачів захистом мінімальної напруги.
Починаючи з моменту
зникає живляча напруга й М1,...,Мn переходять до режиму групового
вибігу, який триває до відключення контакторів магнітних пускачів захистом мінімальної напруги.
Починаючи з моменту  в електромережі спостерігається
примусове зрівняння напруги на затискачах контакторів KМ1,...,KМn,
внаслідок чого між двигунами споживачів протікають зрівнювальні струми
в електромережі спостерігається
примусове зрівняння напруги на затискачах контакторів KМ1,...,KМn,
внаслідок чого між двигунами споживачів протікають зрівнювальні струми 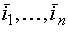 , алгебраїчна сума яких дорівнює нулю:
, алгебраїчна сума яких дорівнює нулю:
| |
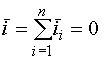 . . |
(7) |
Кожен зрівнювальний струм  може
бути записаний за допомогою операторної провідності ланцюга відповідного двигуна:
може
бути записаний за допомогою операторної провідності ланцюга відповідного двигуна:
| |
 . . |
(8) |
Оскільки при груповому вибігу 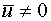 ,
то згідно (7) запишемо:
,
то згідно (7) запишемо:
| |
 , , |
(9) |
де 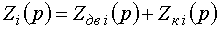 — операторний опір i-го ланцюга
мережі;
— операторний опір i-го ланцюга
мережі;  ,
, 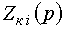 —
операторні опори відповідно i-го двигуна та ГКі.
—
операторні опори відповідно i-го двигуна та ГКі.
У нерухомій системі координат (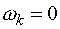 )
операторний опір АД визначається наступним чином [3]:
)
операторний опір АД визначається наступним чином [3]:
| |
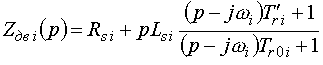 , , |
(10) |
де 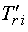 — перехідна стала часу ротора;
— перехідна стала часу ротора;
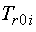 — стала часу, що відповідає ідеальному холостому
ходу при живленні з ротора.
— стала часу, що відповідає ідеальному холостому
ходу при живленні з ротора.
Операторний опір гнучкого кабеля із зазначеними вище параметрами можна
записати:
| |
 . . |
(11) |
З урахуванням наведених залежностей запишемо вираз для відшукання
операторної провідності i-го ланцюга мережі:
| |
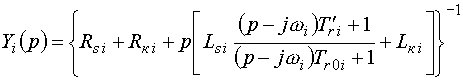 . . |
(12) |
Структурна схема моделі, згідно виразу (12), для відшукання операторної
провідності 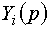 , наведена на рис. 4.
, наведена на рис. 4.

Рис. 4. Структурна схема моделі для визначеня
операторної провідності і-го ланцюга мережі: а) розгорнутий вигляд; б) єдиним блоком
На рис. 5 наведена структурна схема моделі, що реалізує залежність (9).
Вхідними величинами моделі є частоти обертання роторів всіх n двигунів системи під час
вибігу, вихідною — комплексна величина  , тобто блок
(рис. 5б) встановлює залежність:
, тобто блок
(рис. 5б) встановлює залежність:
| |
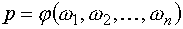 . . |
(13) |
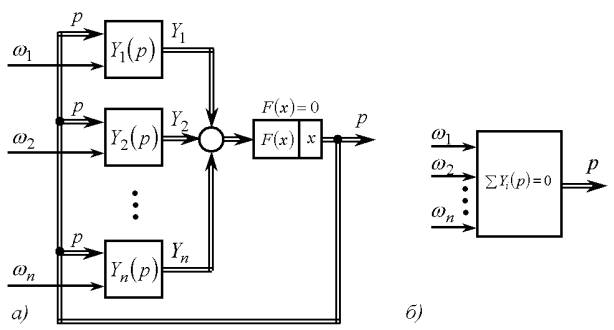
Рис. 5. Структурна схема моделі для визначеня  :
а) розгорнутий вигляд; б) єдиним блоком
:
а) розгорнутий вигляд; б) єдиним блоком
Оскільки частоти обертання роторів під час вибігу змінюються з часом, то
величина 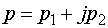 залежить від
залежить від 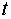 :
:
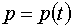 . Це свідчить про те, що
. Це свідчить про те, що 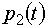 є модулюючим сигналом для частоти напруги
є модулюючим сигналом для частоти напруги 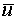 .
.
Вектор напруги у загальній частині мережі, амплітуда якого зменшується
за експоненціальним законом, враховуючи частотну модуляцію, визначається наступним співвідношенням:
| |
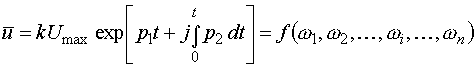 , , |
(14) |
де  — коефіцієнт, що змінюється від 0,83 при
номінальному навантаженні до 0,95 при холостому ході АД перед відключеням [3];
— коефіцієнт, що змінюється від 0,83 при
номінальному навантаженні до 0,95 при холостому ході АД перед відключеням [3];
 — колова частота напруги, що живить систему
до момента відключення.
— колова частота напруги, що живить систему
до момента відключення.
Останній вираз у вигляді структурної схеми наведений на рис. 6.
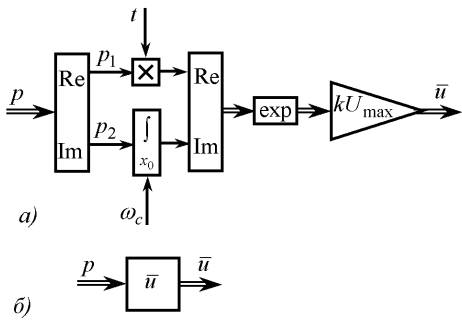
Рис. 6. Структурна схема моделі для
визначеня 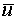 : а) розгорнутий вигляд; б) єдиним блоком
: а) розгорнутий вигляд; б) єдиним блоком
З отриманих структурних блоків (рис. 3б, 5б, 6б) складається узагальнена
структурна схема, яка реалізує математичну модель електротехнічної системи, що розглядається,
при груповому вибігу АД (рис. 7). Наведена модель дійсна з момента відключення автоматичного
вимикача АВ до відключення КМ захистом мінімальної напруги.
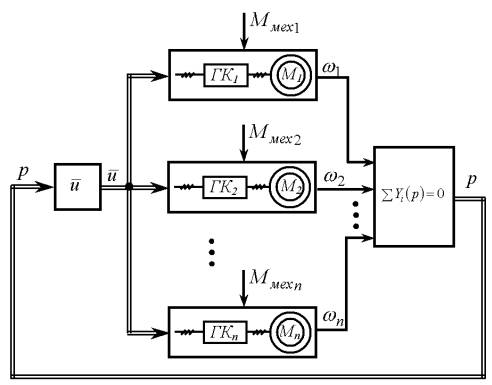
Рис. 7. Узагальнена структурна схема
моделі електротехнічної системи дільниці при груповому вибігу АД
Згідно розробленої моделі для конктерних параметрів елементів системи
(табл. 1) за допомогою обчислювальної техніки були проведені три досліди за умови різної кількості
ланцюгів та різних потужностей АД. Заради спрощення розрахунків приймається, що КМ залишаються
ввімкнені до повної зупинки всіх АД. В результаті моделювання були отримані діаграми (рис. 8)
у відносних одиницях (в.о.).
Табл. 1 Параметри елементів системи для проведення дослідів
| № досліда |
№ ланцюга |
АД |
ГК |
Рисунок |
| Тип |
Рн, кВт |
М/Мн, в.о. |
Режим під час вибігу |
Тип |
lk, м |
| 1 |
1 |
АИУМ255М4 |
55 |
0,6 |
PP |
КГЭШ3х10 |
200 |
8,а |
| 2 |
ЭКВ3,5-180 |
180 |
0,7 |
ГР |
КГЭШ3х70 |
300 |
| 2 |
1 |
ВРП180М4 |
30 |
0,5 |
РР |
КГЭШ3х6 |
100 |
8,б |
| 2 |
АИУМ255М4 |
55 |
0,7 |
ГР |
КГЭШ3х10 |
150 |
| 3 |
ЭКВ3-55 |
55 |
0,6 |
РР |
КГЭШ3х10 |
200 |
| 3 |
1 |
АИУМ255М4 |
55 |
0,1 |
РР |
КГЭШ3х10 |
150 |
8,в |
| 2 |
ЭКВ3-55 |
55 |
0,1 |
РР |
КГЭШ3х10 |
200 |
| 3 |
2ЭДКОФ250LB4 |
110 |
0,1 |
ГР |
КГЭШ3х25 |
100 |
| 4 |
ЭКВ3-180 |
180 |
0,1 |
РР |
КГЭШ3х70 |
300 |
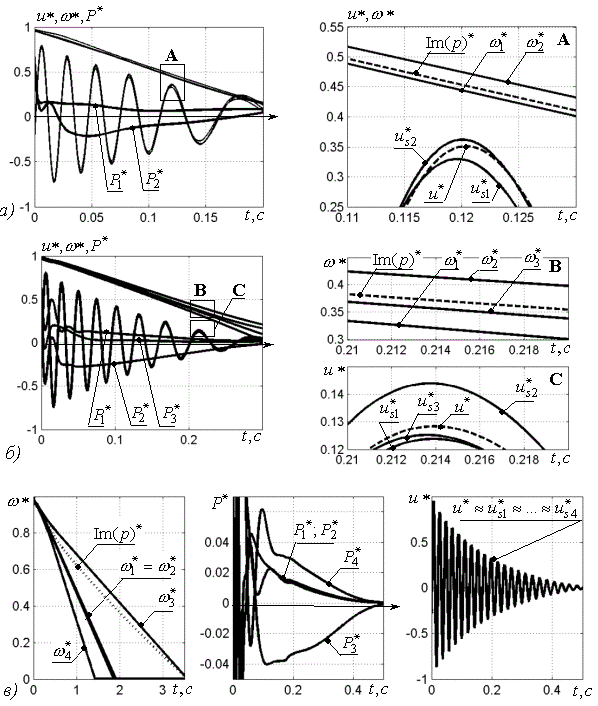
Рис. 8. Діаграми, отримані за допомогою
розробленої моделі, що характеризують вибіг 2х (а), 3х (б) та 4х (в) АД з урахуванням параметрів
ГК: u* — напруга, в.о.; w* — частота обертання, в.о.; P* —
активна потужність двигуна, в.о.
Аналіз отриманих діаграм дозволяє встановити наступне.
1. При груповому вибігу один (або кілька) двигунів переходять до
генераторного режиму роботи (ГР), інші знаходяться у руховому режимі (РР). Про перехід АД до ГР
свідчить, по-перше, перевищення частотою обертання ротора величини  ,
по-друге, від'ємне значення активної потужності двигуна. Наприклад, у випадку рис.
8, а:
,
по-друге, від'ємне значення активної потужності двигуна. Наприклад, у випадку рис.
8, а: 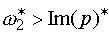 та
та 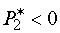 ,
отже М2 знаходиться у ГР.
,
отже М2 знаходиться у ГР.
2. Частота напруги, що обумовлена спільною дією ЕРС обертаня двигунів
мережі під час вибігу, визначається сукупною дією частот обертання роторів усіх вказаних АД.
Характер зміни 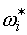 , в свою чергу, залежить від навантаження
та узагальненого коефіцієнту інерції двигунів системи. Наприклад, у випадку досліда №2
(рис. 8, б) величина
, в свою чергу, залежить від навантаження
та узагальненого коефіцієнту інерції двигунів системи. Наприклад, у випадку досліда №2
(рис. 8, б) величина  знижується до 0 за 0,3 с при
навантаженні двигунів
знижується до 0 за 0,3 с при
навантаженні двигунів  , а у випадку досліда №3
(рис. 8, в) навантаження АД складає
, а у випадку досліда №3
(рис. 8, в) навантаження АД складає  і
і
 зменшується до 0 приблизно за 3 с.
зменшується до 0 приблизно за 3 с.
3. Час затухання напруги у загальній мережі визначається параметрами
елементів системи і не залежить від зміни частот обертання роторів двигунів під час групового
вибігу. Для дослідів №2 та №3 різні рівні навантаження двигунів за умови різного діапазона
потужностей практично не впливають на час зменшення напруги — для обох випадків він складає
близько 0,3-0,4с.
Висновки
Отримана математична модель, що дозволяє проводити аналіз процесів у
електротехнічному комплексі дільниці шахти під час групового вибігу АД при аварійному відключенні
системи. Модель враховує як параметри кабельних ліній, так і зміну частот обертання роторів
двигунів з часом.
В ході подальших досліджень доцільно встановити характер впливу ЕРС
обертання двигунів під час групового вибігу на величину витоку струму на землю при відповідному
аварійному режимі.
Перелік посилань
- Риман Я.С. Защита подземных электрических установок угольных шахт. — М.:
Недра, 1977. — 206 с.
- Полесин Я.Л. Причины аварий и травматизма в горной промышленности. — М., Недра, 1969.
- Ковач К.П., Рац. И. Переходные процессы в машинах переменного тока. — М.-Л.:
Госэнергоиздат, 1963. — 744 с.
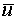 — напруги у
загальній частині мережі;
— напруги у
загальній частині мережі; 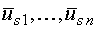 — напруги на затискачах
двигунів М1,...,Мn відповідно;
— напруги на затискачах
двигунів М1,...,Мn відповідно; 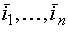 —
зрівнювальні струми у ланцюгах АД споживачів.
—
зрівнювальні струми у ланцюгах АД споживачів.
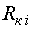 ,
,
 позначають активний опір та індуктивність фази гнучного
кабеля ГКі довжиною
позначають активний опір та індуктивність фази гнучного
кабеля ГКі довжиною 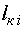 . Усі подальші
розрахунки здійснюватимуться у системі координат статора асинхронного двигуна (
. Усі подальші
розрахунки здійснюватимуться у системі координат статора асинхронного двигуна ( ) та для еквівалентних
двополюсних машин.
) та для еквівалентних
двополюсних машин. .
.
 та
вводячи коефіцієнт затухання
та
вводячи коефіцієнт затухання 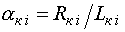 в операторній формі матимемо:
в операторній формі матимемо: .
.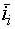 зв'язан з
потокозчепленнями АД виразом:
зв'язан з
потокозчепленнями АД виразом: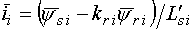 .
.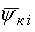 виконується співвідношення:
виконується співвідношення:
 ,
, 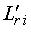 ,
,  ,
,
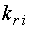 — перехідні індуктивності та коефіцієнти зв'язку
відповідно статора і ротора і-го двигуна.
— перехідні індуктивності та коефіцієнти зв'язку
відповідно статора і ротора і-го двигуна.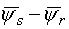 :
: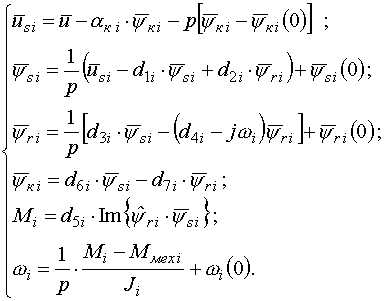

 двигуни
М1,...,Мn споживачів були ввімкнені. У момент
двигуни
М1,...,Мn споживачів були ввімкнені. У момент 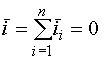 .
. може
бути записаний за допомогою операторної провідності ланцюга відповідного двигуна:
може
бути записаний за допомогою операторної провідності ланцюга відповідного двигуна: .
.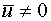 ,
то згідно (7) запишемо:
,
то згідно (7) запишемо: ,
,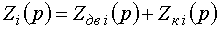 — операторний опір i-го ланцюга
мережі;
— операторний опір i-го ланцюга
мережі;  ,
, 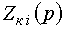 —
операторні опори відповідно i-го двигуна та ГКі.
—
операторні опори відповідно i-го двигуна та ГКі.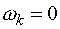 )
операторний опір АД визначається наступним чином [3]:
)
операторний опір АД визначається наступним чином [3]: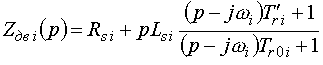 ,
,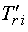 — перехідна стала часу ротора;
— перехідна стала часу ротора;
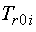 — стала часу, що відповідає ідеальному холостому
ходу при живленні з ротора.
— стала часу, що відповідає ідеальному холостому
ходу при живленні з ротора. .
.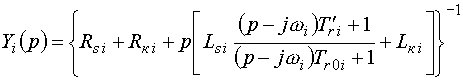 .
.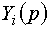 , наведена на рис. 4.
, наведена на рис. 4.
 , тобто блок
(рис. 5б) встановлює залежність:
, тобто блок
(рис. 5б) встановлює залежність: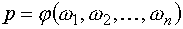 .
.
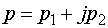 залежить від
залежить від 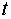 :
:
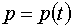 . Це свідчить про те, що
. Це свідчить про те, що 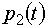 є модулюючим сигналом для частоти напруги
є модулюючим сигналом для частоти напруги 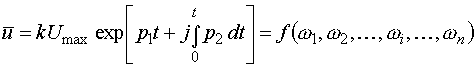 ,
, — коефіцієнт, що змінюється від 0,83 при
номінальному навантаженні до 0,95 при холостому ході АД перед відключеням [3];
— коефіцієнт, що змінюється від 0,83 при
номінальному навантаженні до 0,95 при холостому ході АД перед відключеням [3];
 — колова частота напруги, що живить систему
до момента відключення.
— колова частота напруги, що живить систему
до момента відключення.


 ,
по-друге, від'ємне значення активної потужності двигуна. Наприклад, у випадку рис.
8, а:
,
по-друге, від'ємне значення активної потужності двигуна. Наприклад, у випадку рис.
8, а: 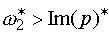 та
та 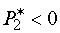 ,
отже М2 знаходиться у ГР.
,
отже М2 знаходиться у ГР.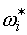 , в свою чергу, залежить від навантаження
та узагальненого коефіцієнту інерції двигунів системи. Наприклад, у випадку досліда №2
(рис. 8, б) величина
, в свою чергу, залежить від навантаження
та узагальненого коефіцієнту інерції двигунів системи. Наприклад, у випадку досліда №2
(рис. 8, б) величина  знижується до 0 за 0,3 с при
навантаженні двигунів
знижується до 0 за 0,3 с при
навантаженні двигунів  , а у випадку досліда №3
(рис. 8, в) навантаження АД складає
, а у випадку досліда №3
(рис. 8, в) навантаження АД складає  і
і