Повернутися до бібліотеки
Вернуться в библиотеку
УДК 621.313.333
МАТЕМАТИЧНА МОДЕЛЬ ЕЛЕКТРОТЕХНІЧНОГО КОМПЛЕКСУ ДІЛЬНИЦІ ШАХТИ ПІСЛЯ ЗАХИСНОГО ВІДКЛЮЧЕННЯ НАПРУГИ
Наукові праці Донецького національного технічного університету.
Серія “Гірнично-електромеханічна”. Випуск 104. — Донецьк: ДонНТУ, 2006. — С.121-128.
Обґрунтована та проаналізована математична модель електротехнічного комплексу дільниці шахти,
що враховує його стан після захисного відключення напруги та дію мінімального захисту пускачів.
The mathematical model of the mine's local electrotechnical system in condition after its
switching-off which takes into account the function of foolling-voltage protection in the starters
was made up and analysed.
Актуальність проблеми та її зв'язок з прикладними задачами
Апаратура автоматичного захисту від витоків струму на землю не повною
мірою забезпечує дотримання параметрів електробезпеки на технологічній дільниці шахти. Причина
полягає в наявності зворотньої ЕРС асинхронних двигунів (АД), підключених до мережі. Цей фактор
електроураження є причиною підтримання у ввімкненому стані контакторів пускачів та збільшення
часу протікання струму в аварійній точці електромережі, що знижує ефективність дії автоматичного
захисту та може призвести до негативних наслідків [1].
Актуальність аналізу процесів в електротехнічному комплексі (ЕТК)
технологічної дільниці шахти після захисного відключення напруги обумовлена необхідністю
удосконалення засобів автоматичного захисту з метою забезпечення у повній мірі прийнятних
параметрів безпеки експлуатації електрообладнання. Це тим більш важливо, що, у зв'язку зі
збільшенням потужності дільничних електроспоживачів, розширення кабельних мереж, застосуванням,
здебільшого, кабелів великого перерізу та переходом на більш високий рівень напруги,
необхідність у підвищенні електробезпеки експлуатації ЕТК дільниць шахти загострилася.
Аналіз досліджень та публікацій
В процесі обгрунтування параметрів реле витоку [1] була встановлена
наявність електроуражуючого фактора з боку зворотньої ЕРС електродвигунів споживачів,
охарактеризовані складові струму через тіло людини в разі її торкання до фази електричної мережі.
Основні принципи побудови математичної моделі одиночного та групового вибігу асинхронних двигунів
викладені в [2]. Однак, наведені аналітичні залежності не повністю враховують особливості вибігу
двигунів в умовах технологічної дільниці шахти. Зокрема, математична модель групового вибігу АД
[3] не враховує відключення магнітних контакторів захистом мінімальної напруги та подальний
одиночний вибіг двигунів, що потребує додаткового вивчення.
Постановка задачі
Задачею досліджень є обґрунтування математичної моделі електротехнічного
комплексу дільниці шахти, що відповідає його стану після захисного відключення мережі та враховує
вплив захисту мінімальної напруги контакторів на характер перехідного процесу в системі.
Основний матеріал та результати досліджень
Після відключення дільничної електромережі апаратурою автоматичного
захисту асинхронні двигуни споживачів, що до цього були ввімкнені, переходять до режиму групового
вибігу, який триває від моменту 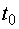 =0 відключення
автоматичного вимикача (АВ) до моменту
=0 відключення
автоматичного вимикача (АВ) до моменту  відключення
контакторів магнітних пускачів захистом мінімальної напруги [1]. Після відключення контакторів
двигуни переходять до режиму одиночного вибігу, який триває до закінчення всіх електромагнітних
та механічних перехідних процесів у кожному АД (моменти
відключення
контакторів магнітних пускачів захистом мінімальної напруги [1]. Після відключення контакторів
двигуни переходять до режиму одиночного вибігу, який триває до закінчення всіх електромагнітних
та механічних перехідних процесів у кожному АД (моменти  ).
).
З метою обґрунтування математичної моделі ЕТК дільниці шахти після
захисного відключення мережі (рис. 1) раціонально скористатися методом суперпозиції, який
передбачає інтегрування математичних моделей групового та одиночного вибігу двигунів споживачів.
Математична модель групового вибігу була розроблена в роботі [3]. Обґрунтуємо модель одиночного
вибігу АД, який триває на інтервалі ( ,
,
 ). Усі подальші розрахунки здійснюватимуться у системі
координат статора асинхронного двигуна (
). Усі подальші розрахунки здійснюватимуться у системі
координат статора асинхронного двигуна (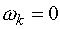 ) для еквівалентних
двополюсних машин.
) для еквівалентних
двополюсних машин.

Рис.1. Схема електротехнічного комплексу дільниці
шахти після захисного відключення:
АВ — автоматичний вимикач; КМ1,...,КМn —
контактори магнітних пускачів; ГК1,...,ГКn — гнучкі кабелі
Під час одиночного вибігу АД струм ротора затухає зі сталою
часу 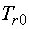 , а його вектор обертається із кутовою
швидкістю
, а його вектор обертається із кутовою
швидкістю  [2]. Відповідна складова потокозчеплення
статора характеризується величиною
[2]. Відповідна складова потокозчеплення
статора характеризується величиною  , що дорівнює:
, що дорівнює:
| |
 , , |
(1) |
де 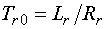 — стала часу, яка відповідає ідеальному неробочому
ходу при живленні з ротора;
— стала часу, яка відповідає ідеальному неробочому
ходу при живленні з ротора;  — частота обертання
ротора в функції часу.
— частота обертання
ротора в функції часу.
Залежність  визначається на основі
рівняння руху двигуна [4]:
визначається на основі
рівняння руху двигуна [4]:
| |
 , , |
(2) |
де 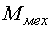 — механічний момент на валу двигуна;
— механічний момент на валу двигуна;
 — приведений момент інерції ротора та навантаження.
— приведений момент інерції ротора та навантаження.
Просторовий вектор напруги статора, що характеризується
величиною  , під час одиночного вибігу визначається
наступним чином:
, під час одиночного вибігу визначається
наступним чином:
| |
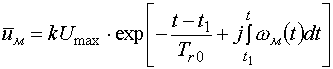 , , |
(3) |
де  — коефіцієнт відношення зворотньої ЕРС до
фазної напруги. Він змінюється від 0,83 при номінальному навантаженні до 0,95 при неробочому
ході АД перед переходом до одиночного вибігу [2];
— коефіцієнт відношення зворотньої ЕРС до
фазної напруги. Він змінюється від 0,83 при номінальному навантаженні до 0,95 при неробочому
ході АД перед переходом до одиночного вибігу [2]; 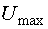 — амплітуда напруги статора у момент переходу до режиму одиночного вибігу.
— амплітуда напруги статора у момент переходу до режиму одиночного вибігу.
Вирази (2) і (3) являють собою математичну модель одиночного вибігу АД.
Структурна схема цієї моделі, що визначає в функциї часу, наведена на рис. 2.
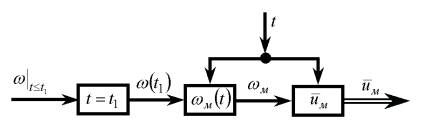
Рис.2. Структурна схема моделі для
визначення 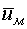 під час одиночного вибігу двигуна
під час одиночного вибігу двигуна
Для розробки інтегрованої математичної моделі ЕТК дільниці шахти після
захисного відключення мережі необхідно обґрунтувати аналітичну функцію, що моделює роботу
контактора пускача. Як свідчить досвід експлуатації, ввімкнений стан контактора зберігається,
якщо напруга в мережі перевищує 0,4 від номінальної ( ).
Виходячи з цього, вихідна характеристика контактора має вигляд:
).
Виходячи з цього, вихідна характеристика контактора має вигляд:
| |
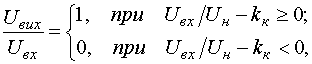 |
(4) |
де 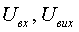 — ефективні значення напруги на вході та виході
контактора;
— ефективні значення напруги на вході та виході
контактора; 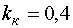 — відносне значення напруги відключення
контактора.
— відносне значення напруги відключення
контактора.
За допомогою функції 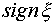 , що визначає
знак аргумента:
, що визначає
знак аргумента:
| |
 |
(5) |
визначимо функцію 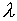 , яка характеризує роботу контактора
згідно вихідної характеристики (4):
, яка характеризує роботу контактора
згідно вихідної характеристики (4):
| |
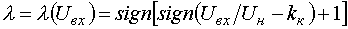 . . |
(6) |
Інверсна до функція визначається наступним чином:
| |
 . . |
(7) |
Структурна схема блоку, що реалізує функцію
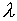 , наведена на рис. 3.
, наведена на рис. 3.
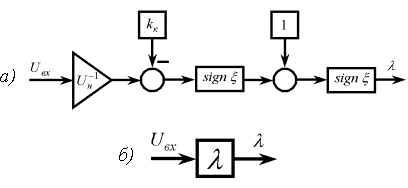
Рис.3. Структурна схема моделі для визначення
функції  :
:
а) розгорнутий вигляд; б) єдиним блоком
Оскільки силове комутаційне електрообладнання споживачів дільниці входить
до складу єдиного ЕТК, напругу на вхідних затискачах усіх контакторів можна важати однаковою.
Це дозволяє використовувати єдину функцію  для
моделювання роботи будь-якого контактора сукупності.
для
моделювання роботи будь-якого контактора сукупності.
У табл. 1 наведені прийняті позначення для складання інтегрованої
математичної моделі дільничного ЕТК, причому  позначає
найбільшу величину серед
позначає
найбільшу величину серед  :
:  .
.
Табл. 1. Прийняті позначення
| Параметр |
Тип вибігу |
| груповий |
одиночний |
комбінований |
| Часовий інтервал |
 |
 |
 |
| Просторовий вектор напруги |
у загальній частині мережі |
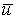 |
— |
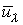 |
| на затискачах і-го двигуна |
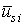 |
 |
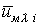 |
| Частота обертання ротора і-го двигуна |
 |
 |
 |
За допомогою функції 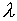 визначаються
параметри системи під час комбінованого вибігу двигунів, який триває на інтервалі
визначаються
параметри системи під час комбінованого вибігу двигунів, який триває на інтервалі 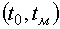 :
:
| |
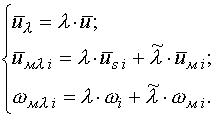 |
(8) |
Два останні рівняння системи (8) раціонально надати у матричній формі:
| |
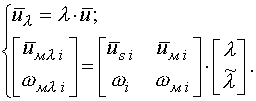 |
(9) |
Перше рівняння системи (9), реалізоване у вигляді структурної схеми,
наведене на рис. 4.
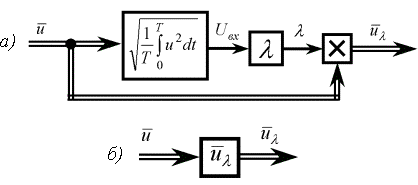
Рис.4. Структурна схема моделі для визначення
просторового вектора напруги у загальній частині мережі під час комбінованого вибігу:
а) розгорнутий вигляд; б) єдиним блоком
Математична модель і-го двигуна системи під час комбінованого
вибігу за умови відомих параметрів системи під час групового вибігу (які обраховуються згідно
[3]) з урахуванням отриманих вище залежностей, має вигляд:
| |
 |
(10) |
Структурна схема блоку, що відповідає математичній моделі (10), наведена
на рис. 5.

Рис.5. Математична модель і-го двигуна
системи під час комбінованого вибігу за умови відомих параметрів системи під час групового вибігу:
а) розгорнутий вигляд; б) єдиним блоком
Отримані залежності (10) у сукупності із математичною моделлю, що була
розроблена в роботі [3], являють собою інтегровану математичну модель ЕТК дільниці шахти після
захисного відключення мережі. Узагальнена структурна схема інтегрованої моделі, що складається
із розроблених вище блоків та блоків, структуру яких обґрунтовано в [3], наведена на рис. 6.

Рис.6. Узагальнена структурна схема інтегрованої
моделі електромеханічного комплексу дільниці шахти після захисного відключення мережі
Згідно розробленої математичної моделі складена та проаналізована
компьютерна модель для випадку комбінованого вибігу двох двигунів, параметри яких наведено
у табл. 2. Отримані діаграми у відносних одиницях (в.о.) наведені на рис. 7. Їх аналіз дозволяє
встановити наступне.
Табл. 2. Прийняті для моделювання параметри елементів системи
| № |
АД |
ГК |
| Тип |
Рн, кВт |
M/Mн, в.о. |
Тип: КГЭШ |
lк, м |
| 1 |
2ЭКВ3,5-90 |
90 |
0,2 |
3х25 |
100 |
| 2 |
2ЭДКОФ250LB4 |
110 |
Під час комбінованого вибігу напруга у загальній частині мережі існує
від момента відключення автоматичного вимикача до момента відключення контакторів споживачів
(рис.7 а). Напруга на затискачах статорів та частоти обертання роторів двигунів на інтервалі
 визначаються умовами групового їх вибігу, а після
моменту
визначаються умовами групового їх вибігу, а після
моменту  — параметрами кожного двигуна окремо,
про що свідчить рис. 7 б,в.
— параметрами кожного двигуна окремо,
про що свідчить рис. 7 б,в.
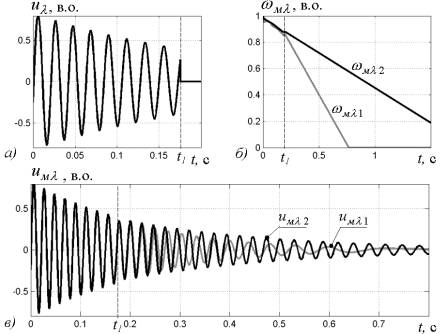
Рис.7. Діаграми, отримані за допомогою
розробленої моделі, що характеризують комбінований вибіг двох двигунів: а) напруга у загальній
частині мережі; б) частоти обертання роторів АД; в) напруга на затискачах статорів
Висновки і напрямок подальших досліджень
В результаті досліджень обґрунтована структура та параметри інтегрованої
математичної моделі електромеханічного комплексу технологічної дільниці шахти після захисного
відключення напруги.
Отримана модель враховує вплив захисту мінімальної напруги контакторів
на характер перехідного процесу. Подальші дослідження мають проводитися у напрямку визначення
впливу ЕРС обертання двигунів дільниці після захисного відключення на величину струму витоку
на землю через тіло людини.
Перелік посилань
- Риман Я.С. Защита подземных электрических установок угольных шахт. — М.:
Недра, 1977. — 206 с.
- Ковач К.П., Рац. И. Переходные процессы в машинах переменного тока. — М.-Л.:
Госэнергоиздат, 1963. — 744 с.
- Сивокобиленко В.Ф., Маренич К.М., Василець С.В. Математичне моделювання
групового вибігу електродвигунів споживачів технологічної дільниці шахти / Наукові
праці Донецького національного технічного університету. Серія "Гірнично-електромеханічна".
Випуск 101. — Донецьк: ДонНТУ, 2005. — С.103-110.
- Андреев В.П., Сабинин Ю.А. Основы электропривода. — М.-Л.: Госэнергоиздат, 1963.
— 772 с.
 =0 відключення
автоматичного вимикача (АВ) до моменту
=0 відключення
автоматичного вимикача (АВ) до моменту  відключення
контакторів магнітних пускачів захистом мінімальної напруги [1]. Після відключення контакторів
двигуни переходять до режиму одиночного вибігу, який триває до закінчення всіх електромагнітних
та механічних перехідних процесів у кожному АД (моменти
відключення
контакторів магнітних пускачів захистом мінімальної напруги [1]. Після відключення контакторів
двигуни переходять до режиму одиночного вибігу, який триває до закінчення всіх електромагнітних
та механічних перехідних процесів у кожному АД (моменти  ).
). ,
,
 ). Усі подальші розрахунки здійснюватимуться у системі
координат статора асинхронного двигуна (
). Усі подальші розрахунки здійснюватимуться у системі
координат статора асинхронного двигуна (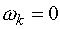 ) для еквівалентних
двополюсних машин.
) для еквівалентних
двополюсних машин.
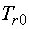 , а його вектор обертається із кутовою
швидкістю
, а його вектор обертається із кутовою
швидкістю  [2]. Відповідна складова потокозчеплення
статора характеризується величиною
[2]. Відповідна складова потокозчеплення
статора характеризується величиною  , що дорівнює:
, що дорівнює: ,
,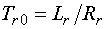 — стала часу, яка відповідає ідеальному неробочому
ходу при живленні з ротора;
— стала часу, яка відповідає ідеальному неробочому
ходу при живленні з ротора;  — частота обертання
ротора в функції часу.
— частота обертання
ротора в функції часу. ,
,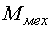 — механічний момент на валу двигуна;
— механічний момент на валу двигуна;
 — приведений момент інерції ротора та навантаження.
— приведений момент інерції ротора та навантаження.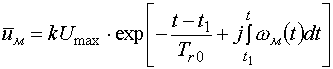 ,
, — коефіцієнт відношення зворотньої ЕРС до
фазної напруги. Він змінюється від 0,83 при номінальному навантаженні до 0,95 при неробочому
ході АД перед переходом до одиночного вибігу [2];
— коефіцієнт відношення зворотньої ЕРС до
фазної напруги. Він змінюється від 0,83 при номінальному навантаженні до 0,95 при неробочому
ході АД перед переходом до одиночного вибігу [2]; 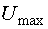 — амплітуда напруги статора у момент переходу до режиму одиночного вибігу.
— амплітуда напруги статора у момент переходу до режиму одиночного вибігу.
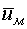 під час одиночного вибігу двигуна
під час одиночного вибігу двигуна ).
Виходячи з цього, вихідна характеристика контактора має вигляд:
).
Виходячи з цього, вихідна характеристика контактора має вигляд: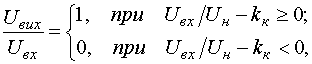
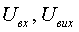 — ефективні значення напруги на вході та виході
контактора;
— ефективні значення напруги на вході та виході
контактора; 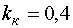 — відносне значення напруги відключення
контактора.
— відносне значення напруги відключення
контактора.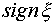 , що визначає
знак аргумента:
, що визначає
знак аргумента:
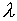 , яка характеризує роботу контактора
згідно вихідної характеристики (4):
, яка характеризує роботу контактора
згідно вихідної характеристики (4):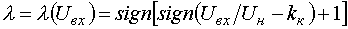 .
. .
.
 :
:  .
.
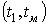

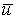
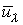
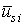

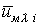



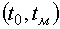 :
: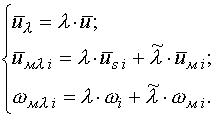
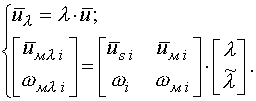




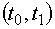 визначаються умовами групового їх вибігу, а після
моменту
визначаються умовами групового їх вибігу, а після
моменту 