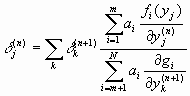|
|
|
Источник – http://www.i2.com.ua/Articles/neural/A_copy/A_copy1.php
ИСПОЛЬЗОВАНИЕ НЕЯВНО ЗАДАННЫХ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ (НПФ) ПРИ ПОСТРОЕНИИ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ. Олександрук Б.О. В данной работе предлагается внедрение неявно заданных передаточных функций при построении нейронных сетей. Также далее исследуются некоторые особенности использования неявно заданных передаточных функций нейронов. В настоящий момент уже исследовано значительное множество моделей нейронных сетей. Ряд моделей нейронных сетей успешно применяются в различных отраслях. Большинство нейросетевых моделей призваны описывать закономерности между входным потоком данных и выходным потоком. Адекватность подбора закономерности нейронной сетью зависит, прежде всего, от структуры сети и передаточных функций нейронов сети. Подробнее остановимся на значимости передаточных функций нейронной сети. Почему передаточные функции нейронов сети так важны? Дело в том, что закономерность, моделируемая нейронной сетью, представляет собой некоторую суперпозицию передаточных функций нейронов сети. Следовательно, важно, чтобы каждая передаточная функция адекватно описывала на микроуровне поведение элементов реальной системы, сгенерировавшей исходные потоки данных. Возьмем часто используемые сигмовидные передаточные функции. Нередко возникают ситуации, когда для адекватного описания элементарных закономерностей такими функциями требуется бесконечное число элементов сети. То же самое касается и полиномиальных передаточных функций. Приведем простой пример. Пусть искомая закономерность соответствует
т.е. половине эллипса. Для того чтобы представить данную функцию в виде суперпозиции сигмовидных функций либо полиномов требуется бесконечное число элементов. С другой стороны, данную функцию можно получить как решение из тривиальной модели ax2+by2=1. Таким образом, сделаем следующий вывод: используя неявную модель можно добиться большей точности при меньшем количестве степеней свободы (параметров) модели, нежели при использовании явно заданной модели. Следовательно, замена явно заданной передаточной функции нейронов является не бесперспективной. Однако с переходом на неявно заданные функции возникает проблема множественных корней, т.е. уравнения модели передаточной функции может иметь несколько корней. Конечно, можно выбирать в качестве решения один из корней, удовлетворяющий определенным условиям. В этом случае функция, которую моделирует нейронная сеть, может иметь разрывы. Чтобы избежать вышеуказанной проблемы рекомендуется использовать уравнение передаточной функции, имеющее единственное решение. Далее целью работы будет построение уравнения передаточной функции, которое имеет единственное решение. Лемма 1.Пусть передаточная функция  задана
уравнением
где  – вектор параметров
передаточной функции,
у – значения выхода нейрона,
Тогда на области  существует единственное
решение
Далее предложим методы адаптации параметров  передаточной функции отдельно взятого нейрона,
используя МНК или рекуррентный метод наименьших квадратов.
Пусть
Определим матрицу
где  - вектор значений входов
нейрона в l-й момент времени,
yl – значения выхода нейронов в l-й момент времени.
Пусть 
Тогда (*) будет иметь единственное решение y.Решая оптимизационную задачу, найдем оценки параметров  передаточной функции нейрона:
Далее, используя оценки параметров , можем построить уравнение неявно заданной передаточной
функции
Тогда для полученных значений параметров существует единственное решение:
согласно лемме 1 при условиях (4) и (5). Решение  является искомой
передаточной функцией нейрона с адаптированными параметрами .
Передаточную функцию можно получить как аналитически, так и численно в зависимости от вида g и f.Для случая, когда функции f и g заданы в виде (1) и (2), оценки параметров можно получить по методу
наименьших квадратов.
Принцип неявно заданных передаточных функций целесообразно использовать в самоорганизующихся сетях МГУА. Также возможно использование данного принципа как в традиционных сетях типа back propagation (в этом случае необходимо дополнительно вычислить  для
неявно заданной передаточной функции) так и в иных моделях нейронных сетей.
Использование принципа неявно заданных передаточных функций практически не отличается от использования явно заданных ПФ для метода группового учета аргумента, поэтому, данный пункт детализировать не будем. Подробнее остановимся на использовании НПФ (неявно заданных передаточных функций) для сетей back propagation.Рассмотрим градиентный метод обучения. Пусть требуется минимизировать следующий критерий:
где   - реальный выход j-го нейрона выходного слоя N нейронной сети при
подаче на вход р-го образа;  - желаемый выход.
Минимизируем критерий методом градиентного спуска:
где  i-й параметр j-го нейрона в
слое.
где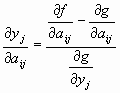 
для g и f, заданных в виде (1) и (2) соответственно
где K- количество нейронов в предыдущем слое n-1.n- текущий слой.
Далее распишем множитель 
как:
где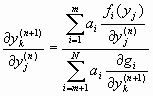 
Если обозначить
Получаем рекуррентную формулу подсчета величины  n-го слоя через последующий n+1-й
слой:
И для простейшего случая градиентного метода получаем корректировку параметров сети (весов):
Использование НПФ позволяет получить новые свойства нейронных сетей и вместе с тем ставит ряд новых задач для дальнейшего исследования искусственных нейронных сетей. Данная работа выполнена в рамках проекта " i2"(http://www.i2.com.ua).Литература:
|
(*)
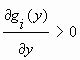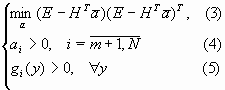
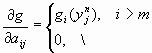
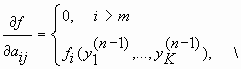
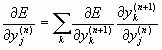(1)
(2)
(**)
,
,
