DonNTU, FCIS
Abstract of master's thesis
«Research
on a data structures in partition problems of large size graphs»
by Krasnokutskaya Maria
Parallel computations allow to increase efficiency and speed of processing of the information at the decision of intricate problems[1]. Efficient use of a distributed memory parallel computer requires that the computational load be balanced across processors in a way that minimizes interprocessor communication. This mapping requirement can be abstracted to a graph problem in which nodes represent computations, edges represent communication - data-flow graph, and the objective is to assign an equal number of edges crossing between processors. Practical experience has shown that the quality of this mapping can have a substantial impact on performance, hence there is considerable interest in effective mapping algorithms - graph partition algorithms.[2] The most popular of them are
- Levelized Nested Dissection[3];
- Kernighan-Lin/ Fiduccia-Mattheyses Algorithm (KL/FM)[2, 3];
- Spectral Methods[1, 2, 3];
- Multilevel Schemes[2, 3].
It is necessary to note, that data-flow graph usually have a sparse adjacency matrix. Partitioning algorithms usually use adjacency matrix or matrices derived from it (e.g. Laplacian matrix in Spectral bisection method), that are sparse too. In a case of graphs of large size (1000, 10000 vertexes) it results in uneconomical use of memory and computing resources in program realization of algorithms.
The purpose of this work is research on a data
structures in partition problems of large size graphs. As researched
algorithm the spectral bisection algorithm is chosen. This spectral
method bisects a graph by considering an eigenvector of an associated
matrix to gain an understanding of global properties of the graph. The
method has recived much attention because it offers a good balance
between generality, quality and efficiency[hendr].
One of ways of solving a problem of redundancy
representation of the graph information is use of multilevel schemes.
Multilevel scheme consists of three phases: graph coarsening, initial
partitioning, and multilevel refinement. In the graph coarsening
phase, a series of graphs is constructed by collapsing together
selected vertices of the input graph in order to form a related
coarser graph. This newly constructed graph then acts as the input
graph for another round of graph coarsening, and so on, until a
sufficiently small graph is obtained. Computation of the initial
bisection is performed on the coarsest (and hence smallest) of these
graphs and so is very fast. Finally, partition refinement is performed
on each level graph, from the coarsest to the finest (i.e. original
graph), using a KL/FM-type algorithm or spectral method [3].
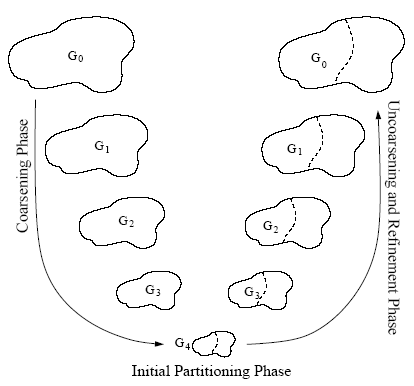 |
Three phases of Mutilevel paradigm |
Other way - use of alternative structures for
matrixes representation. As initial research four data structures were
investigated:
- a two-dimensional array;
- an array of the dynamic arrays;
- three arrays;
- a matrix in format RR(C)O.
|

a) |

b) |
|

c) |
|

d) |
|
Picture – Mehtods of matrix representation;
a) two-dimensional array; b) an array of the dynamic arrays; c)
three arrays; г) matrix in format RR(C)O
|
Specifically, the sparse row-wise format is one
of the most commonly used storage schemes for sparse matrices. A
two-dimensional real matrix A may be represented in RR(C)O by
specifying the three vectors AN, JA and IA [4]:
- AN contains all the
elements of A that have absolute values above the specified
threshold;
- JA is an integer list of the original column indices in A
for the elements in JA (i.e., AN and JA have the same length);
- IA is an integer list which counts the number of nonzero elements in each
row in A. The elements of IX thus specify where in AN and JA to start
looking for the nonzero elements of a given row.
Program realization of these formats has been developed, diagrams
of dependence of time of multiplication of a matrix on a vector from
matrix dimension and its rarity are constructed.

This diagram shows that there is better to use
array of dynamic arrays or RR(C)O format to represent sparse matrixes.
Use of RR(C)U format shows the best results. In following researches
algorithm of spectral bisection will be realized using this formats.
While writing this abstract master's thesis was
not completed yet. Final end - January 2007. The full text of work and
all materials on a theme can be received from the author or her
Scientific adviser after the specified date.
References
-
Bradford L. Chamberlain. Graph
Partitioning Algorithms for DistributingWorkloads of Parallel
Computations, 1998
generals.pdf
(340 Kb)
http://www.cs.washington.edu/homes/brad/cv/pubs/degree/generals.html
-
Bruce Hendrickson, Robert Leland.
Multidimensional Spectral Load Balancing. Sandia National
Laboratories Albuquerque, 1993
hendrickson93multidimensional.pdf
(204 Kb)
http://citeseer.csail.mit.edu/hendrickson93multidimensional.html
-
Kirk Schloegel, George Karypis, Vipin Kumar. Graph
Partitioning for High Performance Scientific
Simulations.University of Minnesota, Department of Computer
Science, Minneapolis, 2000
http://citeseer.ist.psu.edu/schloegel00graph.html
-
SOY/i - Sparse Operations with Yorick/IDL
http://homepage.mac.com/rflicker/soy.htm.



