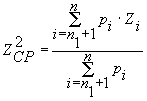1

Конференция "Информатика и компьютерные технологии 2006" Донецкого национального технического университета. Донецк, ДонНТУ Министерство образования и науки Украины, 2006.

Донецкий национальный технический университет, кафедра ВТИ

e-mail:777art@rambler.ru

В этом докладе рассматривается модель оптимизации пропускной способности шахт путем решения задач линейного программирования. Эта модель решает проблемы оптимизации инвестиций. Основная цель - рассмотрение модели оптимизации инвестиции и обоснование оптимальности её применения.

Рассмотрим две группы шахт c технологической структурой и механизмом распределения инвестиций между технологическими звеньями. Первая группа включает  шахт. На этих шахтах добывается энергетический уголь с высокой зольностью. Вторая  группа включает  шахт. На этих шахтах добывается коксующийся уголь с низкой зольностью. Пусть  .  Перенумеруем технологические звенья каждой шахты в порядке возрастания их пропускных способностей. На некотором этапе инвестирования шахта с номером , характеризуется пропускной способностью , эффективностью инвестирования . Зольность угля, добываемого на  –той шахте, обозначим ,  сумму инвестирования, при которой  текущее узкое место технологической цепи  - той шахты ликвидируется на 100%, обозначим  . 

 Сформулируем  вторую вспомогательную задачу, которая используется при построении последовательности инвестирования шахт объединения  , .с целью максимизации суммарной пропускной способности шахт объединения при сохранении средней зольности по двум группам шахтам. Затем опишем методику построения оптимальной последовательности инвестирования, основанную на решении конечной серии  вспомогательных задач для разных значений сумм инвестирования.

1. Вспомогательная задача.  Требуется максимизировать суммарную пропускную способность всех шахт после инвестирования

                 ,                                                                                                           (1)

при ограничении на сумму  инвестирования в целом

      ,                                                                                                                                                 (2)

при условии, что  средняя зольность по шахтам первой группы до инвестирования

не изменится и после инвестирования останется равной средней зольности до инвестирования

,                                                                                                                   (3)

при условии, что  средняя зольность по шахтам второй группы до инвестирования

не изменится и после инвестирования останется равной средней зольности до инвестирования

                 ,                                                                                                           (4)

при фиксированном соотношении между общим количеством энергетического и коксующегося угля до инвестирования и после инвестирования

                                                                              (5)       

Предполагается, что величина инвестиции в каждую шахту не может быть отрицательной

                ,   ,                                                                                                                                    (6)   

а общая сумма инвестирования  такова, что при ее распределении между шахтами ни одно из узких мест не ликвидируется, более чем на 100%

                ,     .                                                                                                                                  (7)

В частности, если для  - той шахты инвестирование осуществляется в объединенный участок, включающий звенья с 1 по ,  то 

              ,      ,                                                                                                               (8)   

где  - пропускная способность ( ) – го звена -той шахты. Если  для некоторой шахты инвестирование осуществляется в объединенный участок, включающий все технологические звенья:  ,  то для этой шахты ограничение (7) не учитывается.

 Отметим¸ что  задача (1)-(6) является стандартной задачей линейного программирования. Условия (7) в стандартную задачу линейного программирования (1)-(6) включать не будем. Эти условия вместе с  (8)  будем использовать для формирования признака окончания расчетов при решении каждой серии вспомогательных задач. 

2. Построение оптимальной последовательности инвестирования.      Каждый член последовательности для модели вычисляется в соответствии с методикой в два этапа. На первом этапе решается серия вспомогательных задач линейного программирования  (1)-(6)     для разных значений   с некоторым шагом   :   ,   и находится  промежуток  ,  внутри которого впервые хотя бы одно из условий (7) выполняется в виде равенства.   На втором этапе непосредственно вычисляется член последовательности  -  минимальное предельное значение суммы инвестирования, при котором ровно одно из условий (7) выполняется в виде равенства, а все остальные условия выполняются в виде строгого неравенства.

Экономико - математические модели оптимального инвестирования монопродуктовых предприятий, могут лежать в основе специализированного программного продукта, они разработаны аппаратом линейного программирования.  Запрограммированное программное математическое обеспечение может легко интегрироваться с модулями ERP (enterprise resource planning планирование ресурсов предприятий) систем. Может происходить анализ результатов моделирования  последовательности и размеров инвестирования предприятий, входящих в объединение.  Полученные результаты позволят оптимально распоряжаться инвестициями на каждом шаге инвестирования и максимально увеличить суммарную пропускную способность предприятий объединения. Предлагаемая технология инвестирования позволит оптимально распределять бюджет, планировать затраты на инвестиционные программы в рамках объединения, контролировать доступные ресурсы, сравнивать фактические издержки с плановыми и т.д. Работа выполнена в рамках концепции [2], которая адаптирована под конкретно поставленную задачу.

Литература

1.Федоренко Р.П.  Приближенное  решение  задач   оптимального  управления. Москва, Наука, 1978, 488 стр.

2.Хайруллин Р.З. Технология исследования управляемых систем. 1999.
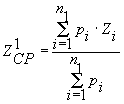
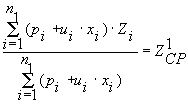