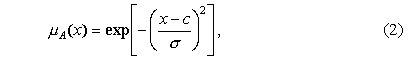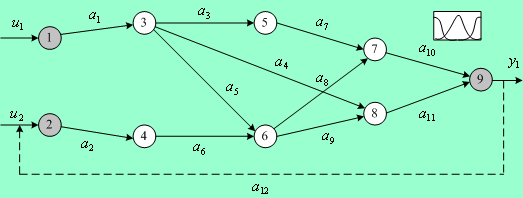
Паклин Николай; Тененев В.А., Якимович Б.А.НЕЧЕТКОЕ МОДЕЛИРОВАНИЕ ДИНАМИЧЕСКИХ СИСТЕМ

http://www.paklin.newmail.ru/mater/fuzzy_din.html

Построение динамической модели сложной системы часто является единственным доступным способом получения информации о ее поведении. Методы моделирования динамических систем зависят от степени информативности поведения системы и ее сложности. Некоторые системы допускают представление в виде дифференциальных уравнений, описывающие какие-либо законы сохранения, действующие в них. В этом случае основной задачей моделирования является подбор коэффициентов, входящих в уравнения, обеспечивающих адекватность математической модели. При исследовании сложных систем, особенно экономических, очень часто не представляется возможным получить достоверную математическую модель из-за большой неопределенности взаимодействий элементов системы. Поэтому в большинстве случаев приходится ограничиваться некоторым статистическим анализом с использованием аппарата математической статистики [1]. Развивающиеся в последнее время методы извлечения знаний из данных позволяют сделать еще один шаг в направлении моделирования сложных систем.

Для описания подобных систем можно применить методы нечеткой логики [2, 3]. Для этого представим динамическую систему в виде нечеткой сети, состоящей из элементов, соединенных между собой связями. Среди элементов системы выделяются входные и выходные переменные, между элементами могут присутствовать обратные связи. На рис. 1 представлен пример модели системы, имеющей 2 входа, один выход и обратную связь, которая изображена пунктирной линией.

Рис. 1. Модели системы в виде нечеткой сети

Обозначим через - вектор входных воздействий; - результирующий вектор. Каждой связи между элементами системы ставится в соответствие нечеткое правило . Каждому правилу соответствуют функции принадлежности условия и следствия. Правила, содержащие одинаковые следствия и относящиеся к одному и тому же взаимодействию, объединяются в одно с помощью логического суммирования. Количественный результат взаимодействия между элементами определяется на основе нечеткого вывода [2]. Представим нечеткое правило в виде , которое в общем случае записывается в виде:

Для определения результирующего уровня активации применяется оператор логического умножения для отдельных составляющих условия в правиле:

Агрегированная по всем правилам функция принадлежности определяется логическим суммированием

а точечная оценка результата вычисляется относительно центра области:

Функционирование такой системы в направлении от входа к выходу определяется зависимостью Y = F(U,W), где W - параметры системы, включая и внешние факторы. При наличии обратной связи в системе функциональная зависимость принимает рекуррентный вид

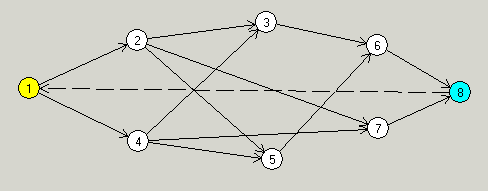
где t - период развития системы.

Построенная имитационная модель позволяет управлять поведением системы при варьировании величин компонент вектора U.

Рассмотрим пример: влияние инвестиций на эффективность работы некоторой производственной системы. Элементами системы являются (рис. 2):

Рис. 2. Модель процесса инвестиций. Пунктирной линией показана обратная связь.

1 - объем инвестиций (входная переменная);
2 - квалификация рабочей силы;
3 - производительность труда;
4 - оборудование;
5 - качество продукции;
6 - доход;
7 - затраты;
8 - суммарный эффект (выходная переменная).
Связи между элементами представлены в виде правил:
(1->2) - влияние инвестиций на квалификацию;
(1->4) - влияние инвестиций на обновление оборудования;
(2->3) - влияние квалификации на производительность труда;
(2->5) - влияние квалификации на качество;
(4->3) - влияние оборудования на производительность труда;
(4->5) - влияние квалификации на качество;
(2->3) - влияние квалификации на производительность труда;
(2->7) - влияние затрат на квалификацию на общие затраты;
(4->7) - влияние затрат на оборудование на общие затраты;
(3->6) - влияние производительности на доход;
(5->6) - влияние качества на доход;
(6->8) - влияние дохода на суммарный эффект;
(7->8) - влияние затрат на суммарный эффект;
(8->1) - влияние суммарного эффекта на инвестиции (обратная связь).
В качестве функции принадлежности правил выберем функцию гауссовского типа, получившей распространение в нечетких сетях [2]. Она описывается формулой

и оперирует двумя параметрами: и c. Параметр c обозначает центр нечеткого множества, а параметр отвечает за крутизну функции. На рис. 3 представлен пример функций принадлежности для правила, описывающего влияние дохода на суммарный эффект.

Рис. 3. Функции принадлежности для правила
"доходы - суммарный эффект"

Подбор таких функций принадлежности может вестись двумя способами. В первом случае эксперты устанавливают меры условия и следствия, а также формулируют правила в виде нечетких высказываний, и система (1) функционирует в экспертном режиме по приведенному выше алгоритму. Данный подход имеет существенный недостаток, заключающийся в субъективности мнений экспертов. При наличии достаточного количества данных, связывающих входные и выходные параметры нечеткой системы, параметры функций принадлежности (2) можно найти в процессе обучения [4].

Пусть имеется P обучающих пар вида (U, D), где - вектор входных переменных; - вектор желаемых выходов. Представленный таким образом обучающий набор данных описывает поведение динамической системы (1) за некоторый промежуток времени T. Тогда нечеткое правило, описывающее межэлементную связь характеризуется множеством параметров функций принадлежности Гаусса (2):

где Vi - количество термов i-го элемента системы, индексы A и B означают параметры функций принадлежности условия и следствия соответственно. Цель обучения состоит в подборе таких параметров функций принадлежности, чтобы усредненная на P выборках среднеквадратичная ошибка системы была минимальной:

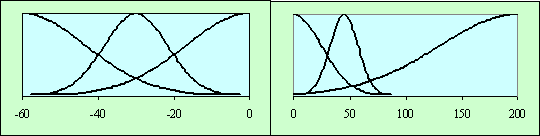
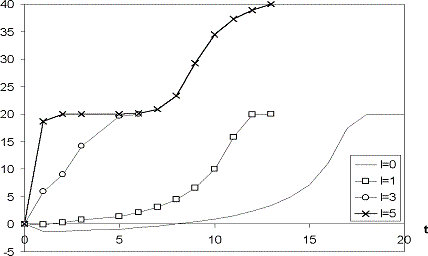
Для минимизации функции (4) следует применить генетический алгоритм [2], использующий только значения целевой функции и решающий проблему наличия многих локальных экстремумов. В результате обучения будут получены оптимальные функции принадлежности системы, что позволит моделировать поведение системы во времени.

На рис. 4 показаны результаты численного моделирования развития описанной выше системы, в которой в качестве входной переменной выступает объем инвестиций. При нулевом значении инвестиций в системе происходит спад и застой эффективности производства в течение продолжительного времени. Увеличение начального объема инвестиций до 3 единиц и более приводит к быстрому повышению эффективности системы.

Рис. 4. Динамика поведения системы в зависимости от
начального объема инвестиций

Представленный подход к формализации нечетких систем был применен при формировании региональной программы развития лесопромышленного комплекса на 2003-2005 гг. [3]. Для этого было разработано программное обеспечение, функционирующее в среде Windows, в котором реализованы возможности графического построения имитационной модели системы, задания правил и функций принадлежности, обучения и вывода динамики развития системы при различных входных воздействиях. Построенная организационно-экономическая имитационная модель лесопромышленного комплекса содержала 40 элементов, из которых 13 - входные воздействия и 5 - выходные переменные, а ее поведение описывалось 62 правилами. См., например, статью "Оптимальное управление детерминированными и нечеткими системами" в разделе Публикации.

Рассмотренный общий подход к моделированию сложными динамическими системами позволяет реализовать оптимальное управление ими в условиях неопределенности. Это достигнуто путем комбинирования методов имитационного моделирования, нечеткой логики и генетических алгоритмов.