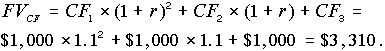|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
В.П. Савчук Финансово-математические основы инвестиционного проектирования http://www.cfin.ru/finanalysis/savchuk/4.shtml 4. Финансово-математические основы инвестиционного проектирования 4. 1. Концепция стоимости денег во времени В основе концепции стоимости денег во времени лежит следующий основной принцип: Доллар сейчас стоит больше, чем доллар, который будет получен в будущем, например через год, так как он может быть инвестирован и это принесет дополнительную прибыль. Данный принцип является наиболее важным положением во всей теории финансов и анализе инвестиций. На этом принципе основан подход к оценке экономической эффективности инвестиционных проектов. Данный принцип порождает концепцию оценки стоимости денег во времени. Суть концепции заключается в том, что стоимость денег с течением времени изменяется с учетом нормы прибыльности на денежном рынке и рынке ценных бумаг. В качестве нормы прибыльности выступает норма ссудного процента или норма выплаты дивидендов по обыкновенным и привилегированным акциям. Учитывая, что инвестирование представляет собой обычно длительный процесс, в инвестиционной практике обычно приходится сравнивать стоимость денег в начале их инвестирования со стоимостью денег при их возврате в виде будущей прибыли. В процессе сравнения стоимости денежных средств при их вложении и возврате принято использовать два основных понятия: настоящая (современная) стоимость денег и будущая стоимость денег. Будущая стоимость денег представляет собой ту сумму, в которую превратятся инвестированные в настоящий момент денежные средства через определенный период времени с учетом определенной процентной ставки. Определение будущей стоимости денег связано с процессом наращения (compounding) начальной стоимости, который представляет собой поэтапное увеличение вложенной суммы путем присоединения к первоначальному ее размеру суммы процентных платежей. В инвестиционных расчетах процентная ставка платежей применяется не только как инструмент наращения стоимости денежных средств, но и как измеритель степени доходности инвестиционных операций. Настоящая (современная) стоимость денег представляет собой сумму будущих денежных поступлений, приведенных к настоящему моменту времени с учетом определенной процентной ставки. Определение настоящей стоимости денег связано с процессом дисконтирования (discounting), будущей стоимости, который (процесс) представляет собой операцию обратную наращению. Дисконтирование используется во многих задачах анализа инвестиций. Типичной в данном случае является следующая: определить какую сумму надо инвестировать сейчас, чтобы получить например, $1,000 через 5 лет. Таким образом, одну и ту же сумму денег можно рассматривать с двух позиций: а) с позиции ее настоящей стоимости б) с позиции ее будущей стоимости Причем, арифметически стоимость денег в будущем всегда выше. 4. 2. Элементы теории процентов В процессе анализа инвестиционных решений принято использовать сложные проценты. Сложным процентом называется сумма дохода, которая образуется в результате инвестирования денег при условии, что сумма начисленного простого процента не выплачивается в конце каждого периода, а присоединяется к сумме основного вклада и в следующем платежном периоде сама приносит доход. Основная формула теории процентов определяет будущую стоимость денег:
где P - настоящее значение вложенной суммы денег, F - будущее значение стоимости денег, n - количество периодов времени, на которое производится вложение, r - норма доходности (прибыльности) от вложения. Простейшим способом эту формулу можно проинтерпретировать, как определение величины депозитного вклада в банк при депозитной ставке r (в долях единицы). Существо процесса наращения денег не изменяется, если деньги инвестируются в какой-либо бизнес (предприятие). Главное, чтобы вложение денег обеспечивало доход, то есть увеличение вложенной суммы. Пример 1.Банк выплачивает 5 процентов годовых по депозитному вкладу. Согласно формуле (4.1) $100, вложенные сейчас, через год станут
Если вкладчик решает оставить всю сумму на депозите еще на один год, то к концу второго года объем его вклада составит
или по формуле (4.1)
Процесс наращения стоимости $100 по годам можно представить в виде таблицы или диаграммы:
Следует отметить, что процесс наращения не является линейным. Настоящее (современное) значение стоимости определенной будущей суммы денег определяется с помощью формулы
которая является простым обращением формулы (4.1). Пример 2 Пусть инвестор хочет получить $200 через 2 года. Какую сумму он должен положить на срочный депозит сейчас, если депозитная процентная ставка составляет 5%. С помощью формулы (4.2) легко определить
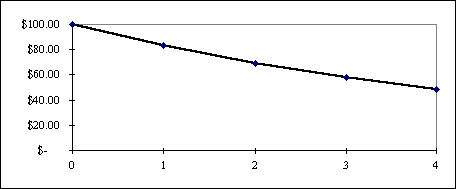
Понятно, что формула (4.2) лежит в основе процесса дисконтирования. И в этом смысле величина r интерпретируется как ставка дисконта и часто называется просто дисконтом. Рассмотренный в примере (4.2) случай можно интерпретировать следующим образом: $181.40 и $200 - это два способа представить одну и ту же сумму денег в разные моменты времени - $200 через два года равносилен $181.40 сейчас. Процесс дисконтирования наглядно можно продемонстрировать с помощью следующего графика:
В анализе инвестиции величины (1+r)nи (1+r)-nчасто называют соответственно множителями наращения и дисконтирования. Наращение и дисконтирование единичных денежных сумм удобно производить с помощью финансовых таблиц 1 и 3, помещенных в приложении. В этих таблицах содержатся множители наращения и дисконтирования, соответственно. 4. 3. Влияние инфляции при определении настоящей и будущей стоимости денег В инвестиционной практике постоянно приходится считаться с корректирующим фактором инфляции, которая с течением времени обесценивает стоимость денежных средств. Это связано с тем, что инфляционный рост индекса средних цен вызывает соответствующее снижение покупательной способности денег. При расчетах, связанных с корректировкой денежных потоков в процессе инвестирования с учетом инфляции, принято использовать два основных понятия
Номинальная сумма денежных средств не учитывает изменение покупательной способности денег. Реальная сумма денежных средств - это оценка этой суммы с учетом изменения покупательной способности денег в связи с процессом инфляции. В финансово-экономических расчетах, связанных с инвестиционной деятельностью, инфляция учитывается в следующих случаях:
В процессе оценки инфляции используются два основных показателя:
Корректировка наращенной стоимости с учетом инфляции производится по формуле
где Fn- номинальная будущая стоимость денег с учетом инфляции. Здесь предполагается, что темп инфляции сохраняется по годам. Если r - номинальная ставка процента, которая учитывает инфляцию, то расчет реальной суммы денег производится по формуле:
то есть номинальная сумма денежных средств снижается в (1+Т)n раза в соответствии со снижением покупательной способности денег. Пример 3.Пусть номинальная ставка процента с учетом инфляции составляет 50%, а ожидаемый темп инфляции в год 40%. Необходимо определить реальную будущую стоимость объема инвестиций 200,000 грн. Подставляем данные в формулу (4.4), получаем
Если же в процессе реального развития экономики темп инфляции составит 55%, то
Таким образом, инфляция “съедает” и прибыльность и часть основной суммы инвестиции, и процесс инвестирования становится убыточным. В общем случае при анализе соотношения номинальной ставки процента с темпом инфляции возможны три случая:
наращение реальной стоимости денежных средств не происходит, так как прирост их будущей стоимости ПОГЛОЩАЕТСЯ инфляцией : реальная будущая стоимость денежных средств возрастает несмотря на инфляцию : реальная будущая стоимость денежных средств снижается, то есть процесс инвестирования становится УБЫТОЧНЫМ.
Взаимосвязь номинальной и реальной процентной ставок. Пусть инвестору обещана реальная прибыльность его вложений в соответствии с процентной ставкой 10 %. Это означает, что при инвестировании 1,000 грн. через год он получит 1,000 х (1+0.10) = 1,100 грн. Если темп инфляции составляет 25 %, то инвестор корректирует эту сумму в соответствии с темпом: 1,100 х (1+0.25) = 1,375 грн. Общий расчет может быть записан следующим образом 1,000 х (1+0.10) х (1+0.25) = 1,375 грн. В общем случае, если rр - реальная процентная ставка прибыльности, а Т - темп инфляции, то номинальная (контрактная) норма прибыльности запишется с помощью формулы
Величина rз + rзT имеет смысл инфляционной премии. Часто можно встретить более простую формулу, которая не учитывает “смешанный эффект” при вычислении инфляционной премии
Эту упрощенную формулу можно использовать только в случае невысоких темпов инфляции, когда смешанный эффект пренебрежимо мал по сравнению с основной компонентой номинальной процентной ставки прибыльности. Отношение к инфляции в реальной практике. Прогнозирование темпов инфляции очень сложный процесс, протекающий на фоне большого количества неопределенностей. Это особенно характерно для стран с неустойчивым экономическим положением. Кроме того, темпы инфляции в отдельные периоды в значительной степени подвержены влиянию субъективных факторов, слабо поддающихся прогнозированию. Поэтому один из наиболее реально значимых подходов может состоять в следующем: стоимость инвестируемых средств и суммы денежных средств, обеспечивающих возврат, пересчитываются из национальной валюты в одну из наиболее устойчивых твердых валют (доллар США, фунт стерлингов Великобритании, немецкие марки). Пересчет осуществляется по биржевому курсу на момент проведения расчетов. Процесс наращения и дисконтирования производится в данном случае не принимая во внимание инфляцию. Конкретная процентная ставка определяется исходя из источника инвестирования. Например, при инвестировании за счет кредитов коммерческого банка в качестве показателя дисконта принимается процентная ставка валютного кредита этого банка. 4. 4. Наращение и дисконтирование денежных потоков Поскольку процесс инвестирования, как правило, имеет большую продолжительность в практике анализа эффективности капитальных вложений, обычно приходится иметь дело не с единичными денежными суммами, а с потоками денежных средств. Вычисление наращенной и дисконтированной оценок сумм денежных средств в этом случае осуществляется путем использования соответствующих формул (4.1) и (4.2) для каждого элемента денежного потока. Денежный поток принято изображать на временной линии в одном из двух способов: А.
В.
Представленный на рисунке денежный поток состоит в следующем: в настоящее время выплачивается (знак “минус”) $2,000, в первый и второй годы получено $1,000, в третий - $1,500, в четвертый - снова $1,000. Элемент денежного потока принято обозначать CFk (от Cash Flow), где k - номер периода, в который рассматривается денежный поток. Настоящее значение денежного потока обозначено PV ( Present Value), а будущее значение - FV ( Future Value). Используя формулу (4.1), для всех элементов денежного потока от 0 до n получим будущее значение денежного потока
Пример 4.После внедрения мероприятия по снижению административных издержек предприятие планирует получить экономию $1,000 в год. Сэкономленные деньги предполагается размещать на депозитный счет (под 5 % годовых) с тем, чтобы через 5 лет накопленные деньги использовать для инвестирования. Какая сумма окажется на банковском счету предприятия? Решим задачу с использованием временной линии.
Таким образом через 5 лет предприятие накопит $5,526, которые сможет инвестировать. В данном случае денежный поток состоит из одинаковых денежных сумм ежегодно. Такой поток называется аннуитетом. Для вычисления будущего значения аннуитета используется формула
которая следует из (4.5) при CFk = const и CF0 = 0. Расчет будущего значения аннуитета может производиться с помощью специальных финансовых таблиц. Фрагмент этих таблиц помещен в приложении (таблица 2). В частности, с помощью таблицы 2 при r = 5% и n = 5 получаем множитель 5,526, который соответствует результату расчета примера. Дисконтирование денежных потоков осуществляется путем многократного использования формулы (4.2), что в конечном итоге приводит к следующему выражению:
Пример 5.Рассмотрим денежный поток с неодинаковыми элементами CF1=100, CF2=200, CF3=200, CF4=200, CF5=200, CF6=0, CF7=1,000, для которого необходимо определить современное значение (при показателе дисконта 6%). Решение проводим с помощью временной линии:
Вычисление дисконтированных значений отдельных сумм можно производить путем использования таблицы 3, помещенной в приложении Дисконтирование аннуитета (CFj = const) осуществляется по формуле
Для расчета настоящего (современного) значения аннуитета может быть использована таблица 4 приложения. Пример 6. Предприятие приобрело облигации муниципального займа, которые приносят ему доход $15,000, и хочет использовать эти деньги для развития собственного производства. Предприятие оценивает прибыльность инвестирования получаемых каждый год $15,000 в 12 %. Необходимо определить настоящее значение этого денежного потока. Решение проведем с помощью таблицы:
По результатам расчетов мы видим, что
Задача может быть решена также с помощью таблицы 4 приложения. При r = 12% и n = 5 по таблице находим множитель дисконтирования 3.605. Современное значение бесконечного (по времени) потока денежных средств определяется по формуле:
которая получается путем суммирования бесконечного ряда,
определяемого формулой (4.8) при 4.5. Сравнение альтернативных возможностей вложения денежных средств с помощью техники дисконтирования и наращения Техника оценки стоимости денег во времени позволяет решить ряд важных задач сравнительного анализа альтернативных возможностей вложения денег. Рассмотрим эту возможность на следующем примере. Пример 7. Комплексное пояснение к временной стоимости денег. Рассмотрим поток $1,000, который генерируется какой либо инвестицией в течение 3 лет. Расчетная норма прибыльности инвестирования денежных средств предприятия составляет 10 %.
Попытаемся последовательно ответить на ряд вопросов, связанных с различными ситуациями относительно этого потока и его использования. Вопрос 1. Какова современная стоимость этого потока?
Вопрос 2. Какова будущая стоимость $2,486.85 на конец 3 года? (то есть если бы мы вложили деньги в банк под r = 10% годовых)?
Вопрос 3. Какова будущая стоимость потока денежных средств на конец 3-го года?
Мы получили одинаковые ответы на второй и третий вопросы. Вывод очевиден: если мы инвестируем в какой-либо бизнес $2,486.85 и эта инвестиция генерирует заданный поток денег $1,000, $1,000, $1,000, то на конец 3-го года мы получим ту же сумму денег $3,310, как если бы просто вложили $2,486.85 в финансовые инструменты под 10% годовых. Пусть теперь величина инвестиции составляет $2,200, а генерируемый поток такой же, что приводит к концу 3-го года к $3,310. Инвестирование $2,200 в финансовые инструменты под 10% даст,
очевидно, Вопрос 4. Как изменится ситуация, если норма прибыльности финансового вложения денег r станет выше, например 12%. По-прежнему мы инвестируем $2,486.85 в бизнес, и это приводит к потоку денежных средств $1,000 каждый год в течение 3-х лет. Современное значение этого потока
уменьшилось и стало меньше исходной суммы инвестиций $2,486.85. Сравним будущее значение исходной суммы $2,486.85 и потока денежных средств, который генерирует инвестирование этой суммы в бизнес:
Выводы, которые можно сделать на основе сравнения этих значений таковы: a) инвестирование суммы $2,486.85 в финансовые инструменты под 12% годовых приведет к $3,493.85 через 3 года, б) инвестирование суммы $2,486.85 в бизнес, который генерирует денежный поток $1,000 каждый год в течение 3-х лет, приведет к $3,374.40 к концу 3-го года. Очевидно, что при норме прибыльности 12% инвестировать в бизнес не выгодно. Данный вывод имеет простое экономическое объяснение. Дело в том, что инвестирование денег в финансовые инструменты начинает приносить доход сразу же, начиная с первого года. В то же время, инвестирование денег в реальные активы позволяет получить первую $1,000 только к концу первого года, и она приносит финансовый доход только в течение оставшихся двух лет. Другими словами, имеет место запаздывание сроков начала отдачи в случае инвестирования реальные активы по сравнению с инвестицией в финансовые инструменты. И если при норме прибыльности 10 процентов оба варианта вложения денег равносильны в смысле конечной суммы “заработанных” денег, то увеличение нормы прибыльности делает инвестицию в финансовые инструменты более выгодной. Возвратимся к количественному сравнению эффективности альтернативного вложения денег. Рассмотрим, насколько выгоднее вкладывать деньги в финансовые инструменты по сравнению с реальными инвестициями в двух временных точках: момент времени “сейчас” и конец третьего года. В настоящее время поток денежных средств от реальной инвестиции составляет $2,401.83 при исходной инвестиции $2,486.85. Значит финансовая инвестиция более выгодна на $85. К концу третьего года финансовая инвестиция принесет $3,493.85, а реальная инвестиция - $3,374.40. Разница составляет $119.45. Существенно подчеркнуть, что это различие также подчиняется концепции стоимости денег во времени, т.е. продисконтировав $119.45 при 12 процентах мы закономерно получим $85 |
|||||||||||||||||||||||||||||||||||||||||||||||||||
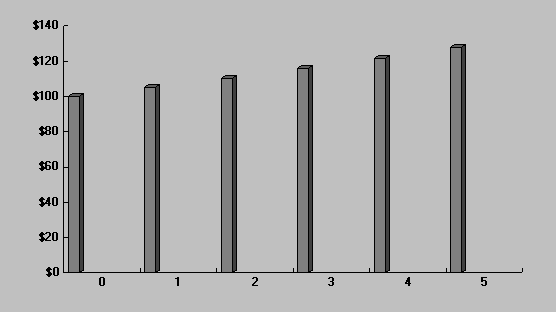

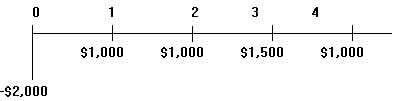
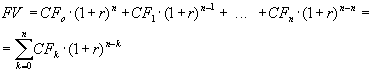 (4.5)
(4.5)