|
F. Benjamin Zhan Three Fastest Shortest Path Algorithms on Real Road Networks: Data Structures and ProceduresSourсe:
Abstract It is well known that computing shortest paths over a network is an important task in many network and transportation related analyses. Choosing an adequate algorithm from the numerous algorithms reported in the literature is a critical step in many applications involving real road networks. In a recent study, a set of three shortest path algorithms that run fastest on real road networks has been identified. These three algorithms are: 1) the graph growth algorithm implemented with two queues, 2) the Dijkstra algorithm implemented with approximate buckets, and 3) the Dijkstra algorithm implemented with double buckets. As a sequel to that study, this paper reviews and summarizes these three algorithms, and demonstrates the data structures and procedures related to the algorithms. This paper should be particularly useful to researchers and practitioners in transportation, GIS, operations research and management sciences. Acknowledgments This research was supported in part by a Faculty Research Enhancement Grant from Southwest Texas State University and in part by a copy of UNIX Arc/Info from Environmental Systems Research Institute, Inc (ESRI). The author also wishes to thank Boris V. Cherkassky, Andrew V. Goldberg and Tomasz Radzik for making their one-to-all shortest paths C source codes available. Contents
2. Recent Evaluations of Shortest Path Algorithms
2.2 Zhan and Noon's Evaluation 2.3 Three Fastest Algorithms on Real Road Networks 3. Network Representations, the Labeling Method and Data Structures Related to Shortest Path Algorithms 4. The Graph Growth Algorithm Implemented With Two Queues 5. The Dijkstra's Algorithm Implemented With Approximate and Double Buckets 6. Concluding Remarks References 1. Introduction
With the development of geographic information systems (GIS) technology, network and transportation analyses within a GIS environment have become a common practice in many application areas. A key problem in network and transportation analyses is the computation of shortest paths between different locations on a network. Sometimes this computation has to be done in real time. For the sake of illustration, let us have a look at the case of a 911 call requesting an ambulance to rush a patient to a hospital. Today it is possible to determine the fastest route and dispatch an ambulance with the assistance of GIS. Because a link on a real road network in a city tends to possess different levels of congestion during different time periods of a day, and because a patient's location can not be expected to be known in advance, it is practically impossible to determine the fastest route before a 911 call is received. Hence, the fastest route can only be determined in real time. In some cases the fastest route has to be determined in a few seconds in order to ensure the safety of a patient. Moreover, when large real road networks are involved in an application, the determination of shortest paths on a large network can be computationally very intensive. Because many applications involve real road networks and because the computation of a fastest route (shortest path) requires an answer in real time, a natural question to ask is: Which shortest path algorithm runs fastest on real road networks? Although considerable empirical studies on the performance of shortest path algorithms have been reported in the literature (Dijkstra 1959; Dial et al. 1979; Glover et al. 1985; Gallo and Pallottino 1988; Hung and Divoky 1988; Ahuja et al. 1990; Mondou et al. 1991; Cherkassky et al. 1993; Goldberg and Radzik 1993), there is no clear answer as to which algorithm, or a set of algorithms runs fastest on real road networks. In a recent study conducted by Zhan and Noon (1996), a set of three shortest path algorithms that run fastest on real road networks has been identified. These three algorithms are: 1) the graph growth algorithm implemented with two queues, 2) the Dijkstra algorithm implemented with approximate buckets, and 3) the Dijkstra algorithm implemented with double buckets. As a sequel to that study, this paper reviews and summarizes these three algorithms, and demonstrates the data structures and implementation strategies related to the algorithms. The rest of the paper is organized as follows. Recent evaluations, particularly the evaluation of 15 shortest path algorithms using real road networks, are briefly reviewed in Section 2. Network representation, the labeling method and data structures related to shortest path algorithms in general are reviewed in Section 3. The graph growth algorithm implemented with two queues is described in detail in Section 4.; The approximate and double bucket implementations of the Dijkstra algorithm are reviewed in Section 5. Concluding remarks are given in Section 6. 2. Recent Evaluations of Shortest Path Algorithms A network is defined as a directed graph G = (N, A) consisting of a set N of nodes and a set A of arcs with associated numerical values, such as the number of nodes, n=|N|, the number of arcs, m=|A|, and the length of an arc connecting nodes i and j, denoted as l(i,j). The shortest path problem can be stated as follows: given a network, find the shortest distances (least costs) from a source node to all other nodes or to a subset of nodes on the network. These shortest paths represent a directed tree T rooted from a source node s with the characteristic that a unique path from s to any node i on the network is the shortest path to that node (Ahuja et al. 1993). The length of the shortest path from s to any node i is denoted as d(i). This directed tree is called a shortest path tree. For any network with n nodes, one can obtain n distinctive shortest path trees. Shortest paths from one (source) node to all other nodes on a network are normally referred as one-to-all shortest paths. Shortest paths from one source node to a subset of the nodes on a network can be defined as one-to-some shortest paths. Shortest paths from every node to every other node on a network are normally called all-to-all shortest paths. 2.1 Cherkassky et al.'s Evaluation Although there have been a number of reported evaluations of shortest path algorithms in the literature (e.g., Glover et al. 1985; Gallo and Pallottino 1988; Hung and Divoky 1988), a recent study by Cherkassky et al. (1993) is one of the most comprehensive evaluations of shortest path algorithms to date. They evaluated a set of 17 shortest path algorithms. In their experiment, Cherkassky et al. coded the 17 algorithms using the C programming language, and tested the C programs on a SUN Sparc-10 workstation One-to-all shortest paths can be computed by these C programs. Readers are referred to the Cherkassky et al. (1993) paper for more detailed descriptions about the implementation of the algorithms. Cherkassky et al. used a number of simulated networks with various degrees of complexity for evaluating the algorithms. The results of their studies suggest that no single algorithm performs consistently well on all simulated networks. 2.2 Zhan and Noon's Evaluation More recently, Zhan and Noon (1996) tested 15 of the 17 shortest path algorithms using real road networks. In their evaluation, Zhan and Noon dropped two of the 17 algorithms tested by Cherkassky et al. They did not consider the special-purpose algorithm for acyclic networks because an arc on real road networks can be treated bi-directional, and hence real road networks contain cycles. They also dropped the implementation using a stack to maintain labeled Table 1 - Summary of the 15 Algorithms Evaluated
nodes (see the next section for descriptions about stack and labeled nodes) because they found that this algorithm is many times slower than the rest of the algorithms on real road networks during their preliminary testing. These 15 algorithms are summarized in Table 1. It is not the intention of this paper to review these 15 algorithms thoroughly. Detailed description of the algorithms can be found in Cherkassky et al. (1993) and the references therein. In their evaluation, Zhan and Noon used 21 real road networks for evaluating the shortest path algorithms. These 21 networks included the U.S. National Highway Planning Network (NHPN) covering the continental U.S. and 20 state-level road networks generated from road networks in 10 states in the Midwest and Southeast of the United States. The 10 states are Alabama (AL), Florida (FL), Georgia (GA), Iowa (IA), Louisiana (LA), Minnesota (MN), Missouri (MO), Mississippi (MS), Nebraska (NE), and South Carolina (SC). The 20 state-level road networks are composed of 10 low-detail road networks and 10 high-detail road networks. The 10 low-detail networks contain three levels of roads, including interstate highways, principal arterials and major arterials. The 10 high-detail networks consist of one additional level of more detailed roads in addition to the three levels of roads contained in the low-detail networks. The 21 networks were stored and maintained in Arc/Info GIS running on a SUN Sparc-20 workstation under the Solaris 2.4 environment. The nodes, arcs and arc lengths were downloaded from Arc/Info into ASCII files. Before downloading, a check was made to ensure that the networks were fully connected. A summary of the 21 networks used in Zhan and Noon's evaluation is given in Table 2. One important characteristic of a real road network is the degree of connectivity measured by the arc-to-node ratios. It can be seen in Table 2 that the arc-to-node ratios range from 2.66 to 3.28 in the 21 networks. The degree of connectivity in these 21 networks differ considerably from that of simulated networks where the arc-to-node ratios can be as high as 10 (cf., Gallo and Pallottino 1988). In addition, there is no notable difference in the degrees of connectivity in all 21 networks. Because the number of scans in constructing a shortest path tree is directly related to arc-to-node ratios, it is very important to observe this difference between the arc-to-node ratios in real road networks and simulated networks. The 15 algorithms were coded in the C programming language. The C programs were based on the set of one-to-all shortest path C programs provided by Cherkassky et al. (1993). The set of one-to-all shortest path C codes were modified to automatically generate all-to-all shortest paths. The C programs were compiled with the gcc compiler version 2.5.6 using the O4 optimization option. Zhan and Noon's experiments were conducted on a SUN Sparc-20 workstation (model HS21 with a 125MHz Hypersparc processor and 64 Megabytes of RAM running under the Solaris 2.4 environment). More detailed description about the experiments can be found in Zhan (1995) and Zhan and Noon (1996). 2.3 Three Fastest Algorithms on Real Road Networks Based on their evaluation, Zhan and Noon suggested that the best performing implementation for solving the one-to-all shortest path problem is Pallottino's graph growth algorithm implemented with two queues (TQQ). They further suggested that when the goal is to obtain a one-to-one shortest path or one-to-some shortest paths, the Dijkstra algorithm offers some advantages because it can be terminated as soon as the shortest path distance to the destination node is obtained (see Section 5). Zhan and Noon recommended two of Dijkstra implementations. The choice between the two implementations depends on the maximum network arc lengths. They recommended the approximate buckets implementation of the Dijkstra algorithm (DKA) for computing one-to-some shortest paths over networks whose maximum arc length is less than 1500. For networks whose maximum arc length is greater than 1500, they recommended that the double buckets implementation of the Dijkstra algorithm (DKD) should also be considered. Table 2 - Summary of the 21 real road networks used in the evaluation
Note: The first 10 networks are low-detail road networks (three levels of roads) from the ten states. The remaining 11 networks are the 10 high-detail road networks (four levels of roads) from the ten states plus the US National Highway Planning Network (US). The networks are ordered by the number of nodes (After Zhan and Noon 1996). 3. Network Representations, the Labeling Method and Data Structures Related to Shortest Path Algorithms The way in which an input network is represented and implemented in a shortest path algorithm is vital to the performance of the algorithm. Past research has proven that the forward star representation is the most efficient data structure for representing networks (Gallo and Pallottino 1988; Ahuja et al. 1993 p.35-36; Cherkassky et al. 1993). Two sets of arrays are used in the forward star data structure. The first array is used to store data associated with arcs, and the second array is used to store data related to nodes. All arcs of a network in question are maintained in a list and are ordered in a specific sequence. That is, arcs emanating from nodes 1, 2, 3, ..., are ordered sequentially. Arcs emanating from the same node can be ordered arbitrarily, however. All information associated with an arc, such as starting node, ending node, cost, arc length and capacity are stored with the arc in some way (e.g., corresponding arrays or linked lists). For the array of nodes, a total of n+1 elements are needed. The i-th element associated with node i, pointer(i), stores the sequential number (in the above arc list) of the first arc emanating from node i. There are a few exceptions: 1) for a node i that has no outgoing arc, pointer(i) is set equal to the content of the next element in the array, i.e., pointer(i) = pointer(i+1); and 2) for consistency, the following convention is adopted, i.e., pointer(1)=1 and pointer(n+1)=m+1. The labeling method is a central procedure in most shortest path algorithms (Gallo and Pallottino 1988; Ahuja et al. 1993, p.96). The output of the labeling method is an out-tree from a source node, s, to a set of nodes. This out-tree is constructed iteratively, and the shortest path from s to i is obtained upon termination of the method. Three pieces of information are maintained for each node i in the labeling method while constructing a shortest path tree: the distance label, d(i), the parent node, p(i), and the node status, S(i). The distance label, d(i), stores the upper bound of the shortest path distance from s to i during iteration. Upon termination of an algorithm, d(i) represents the unique shortest path from s to i. The parent node p(i) records the node that immediately precedes node i in the out-tree. The node status, S(i), can be one of the following: unreached, temporarily labeled and permanently labeled.When a node is not scanned during the iteration, it is unreached. Normally the distance label of an unreached node is set to positive infinite. When it is known that the currently known shortest path of getting to node i is also the absolute shortest path we will ever be able to attain, the node is called permanently labeled. When further improvement is still expected to be made on the shortest path to node i, node i is considered only temporarily labeled. It follows that d(i) is an upper bound on the shortest path distance to node i if the node is temporarily labeled; and d(i) represents the final and optimal shortest path distance to node i if the node is permanently labeled. At the beginning of the
iterations in the labeling method, a directed out-tree is initialized and the
initial values of the above parameters d(i), p(i) and S(i)
are set for source node s and every other node i accordingly (Ahuja
et al. 1993). During the scanning process, when a node i
is scanned, the distance label of a successor node j is checked and
an attempt is made to lower the distance label, d(j), of node
j. If d(j) can be lowered, the out-tree is updated by
changing the parent node of j to i, that is, p(j) =
i. Because d(j) is lowered, node j should ultimately
become permanently labeled. The iteration continues until all nodes
become permanently labeled. Upon termination of the iterations, the
out-tree becomes a shortest path tree. Formally, the scanning operation
for node i can be described below. 3.3 Selection Rules and Data Structures The performance of a particular shortest path algorithm partly depends on how the basic operations in the labeling method are implemented. Two aspects are particularly important to the performance of a shortest path algorithm: 1) the strategies used to select the next temporarily labeled node to be scanned, and 2) the data structures utilized to maintain the set of labeled nodes. We briefly review these two aspects in this subsection. Readers can refer to Gallo and Pallottino (1988) and Ahuja et al. (1993) for more detailed discussions on these topics. Strategies commonly used for selecting the next temporarily labeled node to be scanned are "First In First Out" (FIFO), "Last In First Out" (LIFO) and "Best-First-Search" (Gallo and Pallottino 1988). It is fairly easy to see from the names of the first two search strategies that the oldest node in the set of temporarily labeled nodes is selected first in a FIFO search strategy and the newest is selected first in a LIFO strategy at each iteration. In the best-first-search strategy, the node with the minimum distance label from the set of temporarily labeled nodes is considered as the best node. A number of data structures can be used to manipulate the set of temporarily labeled nodes in order to support these strategies. These data structures include arrays, singly and doubly linked lists, stacks, buckets and queues. Detailed definitions and operations related to these data structures are standard knowledge and are well documented in the literature (e.g., Sedgewick 1990; Ahuja et al. 1993, pp.765-787). Therefore, we only selectively review some of them. A singly linked list contains a collection of elements. Each element has a data field and a link field. The data field contains information to be stored, and the link field contains a pointer pointing to the next element in the list. A doubly linked list differs from a singly linked list in that each element in a doubly linked list contains two pointers. One pointer points to the previous element in the list, and another pointer points to the next element in the list. Stack is another special type of list which only allows removal and addition of an element at one end of the list. This end of the list is normally called the top of a stack. The bucket data structure is described in detail in Section 5 because it is related to two of the three recommended algorithms, namely, the approximate and double bucket implementations of the Dijkstra algorithms. A queue is a special type of list which allows the addition of an element at the tail and the deletion of an element at the head. A priority queue is a special type of queue. Each element in a priority queue contains a label (normally a numerical value) that can be used to determine the priority of the element in the queue. Three operations are normally defined in a priority queue: adding a new element, removing the element that has the highest priority in the queue, and correcting the label of an element whose location in the queue is known. When the label of an element in a priority queue is set to the distance label of a node, a priority queue can be used to maintain the set of temporarily labeled nodes efficiently. Therefore, a priority queue is often used to implement the best-first search strategy. A priority queue can be implemented by linked lists, binary-heaps, d-heaps and Fibonacci heaps (Ahuja et al. 1993). The deque and two queue data structures described in the next section are particular types of priority queues which are related to the graph growth algorithm implemented with two queues. 4. The Graph Growth Algorithm Implemented With Two Queues We
describe the data structures and basic procedures related to the graph growth
algorithm implemented with two queues in this section. The two bucket
implementations of the Dijkstra algorithm are described in the next
section. The graph growth algorithm implemented with two queues (TQQ) was
introduced by Pallottino in 1984. TQQ is an improved version of the growth
graph implementation developed by Pape (PAP) in 1974. Before we discuss
these two implementations, let us review the basic procedure in constructing a
shortest path tree as shown below (see, e.g., Pallottino
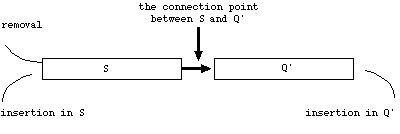
1984, p.259). The four basic operations involved in this procedure are: Queue_Initialization(Q) initialize queue Q; Queue_Removal(Q, i) remove node i from queue Q; Queue_Insertion(Q, j) insert node j into queue Q; and Q = Null? check whether queue Q is empty. The major difference between TQQ and PAP is in the Queue_Insertion(Q, j) operation. In the implementations of PAP and TQQ, nodes are partitioned into two sets: the first set of nodes are those nodes whose current distance labels have not already been used to find a shortest path and the second set contains the remaining nodes. The first set of nodes is maintained by a priority queue Q. Nodes in the second set are further split into two categories: 1) the unreached nodes which have never entered Q, i.e., nodes whose distance labels are still infinite, and 2) labeled nodes, i.e., the nodes that have passed through Q at least once, and the nodes whose current distance labels have already been used. Pape (1974) used a data structure called deque (Q) to maintain the first set of nodes in Q. A deque is illustrated in Figure 1 (Pallottino 1984, p.261). A deque allows insertions at either end of the queue. In the PAP implementation, the deque consists of a LIFO stack (S) and a FIFO queue (Q'). For any node that is not already in Q, the node is inserted at the end of Q' if it is unreached; or the node is inserted at the beginning of S if it is temporarily labeled. Therefore, the basic operations in the PAP implementation can be summarized below: Queue_Initialization(Q) initialize queue Q; Queue_Removal(Q,
i) remove node i from the beginning of queue
Q, Queue_Insertion(Q,
j) For any node j that is not already in Q,
Q = Null? check whether queue Q is empty.
It follows
that for any node that is not already in Q, the node is inserted at the end of
Q' if it is unreached, or the node is inserted at the end of Q" if it is
temporarily labeled. This leads to the following change in the
Queue_Insertion(Q, j) operation of the PAP implementation (Pallottino
1984, p.264). Other operations remain the same. 5. The Dijkstra's Algorithm Implemented With Approximate and Double Buckets The original Dijkstra algorithm partitions all nodes into two sets: temporarily and permanently labeled nodes. At each iteration, it selects a temporarily labeled node with the minimum distance label as the next node to be scanned (Dijkstra 1959; Ahuja et al. 1993, p.109). Once a node is scanned, it becomes permanently labeled. The Dijkstra algorithm terminates when all nodes become permanently labeled. The Dijkstra algorithm is similar to the procedure for constructing a shortest path tree described in Section 4 except for the differences mentioned above. Therefore, detailed procedure of the Dijkstra algorithm is not described further in this paper. In Dijkstra's original algorithm, temporarily labeled nodes are treated as a nonordered list. This is equivalent to treating the priority queue Q in the above general procedure for shortest path tree construction as a nonordered list. This is of course a bottleneck operation because all nodes in Q have to be visited at each iteration in order to select the node with the minimum distance label. A natural enhancement of the original Dijkstra algorithm is to maintain the labeled nodes in a data structure in such a way that the nodes are sorted by distance labels. The bucket data structure is just one of those structures. Buckets are sets arranged in a sorted fashion (Figure 3).
It can be seen that the memory requirement in DKB can be prohibitively large when both C and n are large. However, the memory requirement in DKB can be reduced using either the overflow bag implementation (DKM) or the approximate buckets implementation (DKA) as described by Cherkassky et al. (1993, p.7). The overflow bag implementation maintains only a<(C+1) buckets where a is an input parameter. Only temporarily labeled nodes whose distance labels fall within the range of [a(i), a(i)+a-1] are contained in the buckets at the i-th stage of the algorithm. Other nodes are maintained in a separate set referred to as the overflow bag. Initially, the values of i and a(i) are set to 0. When there is no labeled node left in the given range, i is incremented by one and a(i) is set equal to the minimum of the distance label of the temporarily labeled nodes. The nodes with distance labels within the new range of [a(i), a(i)+a-1] are moved into their corresponding buckets from the overflow bag, and another cycle of the scanning process begins. The Dijkstra's algorithm implemented with approximate buckets (DKA): In the approximate bucket implementation of the Dijkstra algorithm (DKA), a bucket i contains those temporarily labeled nodes with distance labels within the range of [i*b, (i+1)* b-1], where b is a chosen constant. Here approximate means that the values of the distance labels in a bucket are not exactly the same as in the case of DKB, but are within a certain range. Nodes in each bucket are maintained in a FIFO queue. Algorithm DKA requires a total of largerInteger(C/b)+1 buckets. The worst case complexity of DKA is O(mb+n(b+C/b)). It can be seen that this algorithm trades speed for space. Each node can be scanned more than once, but a node cannot be scanned more than b times. The Dijkstra's algorithm implemented with double buckets (DKD): The double bucket implementation of the Dijkstra's algorithm (DKD) combines the ideas of the above two algorithms DKM and DKA. Two levels of buckets, high-level and low-level, are maintained in the DKD implementation. A total of d buckets in the low-level buckets are used. A bucket i in the high-level buckets contains all nodes whose distance labels are within the range of [i*d, (i+1)* d-1]. In addition, a nonempty bucket with the smallest index L is also maintained in the high-level buckets. A low-level bucket d(j)-L*d maintains nodes whose distance labels are within the range of [L*d, (L+1)* d-1]. Nodes in the low-level buckets are examined during the scanning process. After all nodes in the low-level buckets are scanned, the value of L is increased. When the value of L increases, nodes in the nonempty high-level buckets are moved to its corresponding low-level buckets, and the next cycle of scanning process begins. In recent years, we have witnessed an increasing popularity of transportation related decision analysis within a GIS environment (see, e.g., Ralston et al. 1994; Erkut 1996 and Noon et al. 1996). In this type of analysis, the computation of shortest paths is often a central task because shortest path distances are often needed as input for "higher level" models in many transportation analysis problems such as facility location, network flows, vehicle routing and product delivery, just to name a few. In addition, the shortest path problem usually captures the essential elements of more complicated transportation analysis problems. Hence, it can often be used as a benchmark or a starting point for solving more complicated problems in transportation analysis. With the advancement of GIS technology and the availability of high quality road network data, it is possible to conduct transportation analysis concerning large geographic regions within a GIS environment. Sometimes, this type of analysis has to be completed in real time. As a consequence, these analysis tasks demand high performance shortest path algorithms that run fastest on real road networks. Although there has been considerable reported research related to the evaluation of the performance of shortest path algorithms, there has been no clear answer as to which algorithm or a set of algorithms runs fastest on real road networks in the literature. A recent evaluation of shortest path algorithms using real road networks has identified a set of three algorithms that run fastest. These three algorithms are: 1) The Graph Growth Algorithms implemented with two queues (TQQ), 2) The Dijkstra's algorithm implemented with approximate buckets (DKA), and 3) The Dijkstra's algorithm implemented with double buckets (DKD). As a sequel to that earlier evaluation, this paper has reviewed and summarized the data structures and procedures related to the three algorithms. This paper provides a direct source that summarizes a set of shortest path algorithms that run fastest on real road networks. This source should be particularly useful for researchers and practitioners whose research and practice are related to the use of shortest path algorithms.
|