3.1 Введение
Однажды данные изображения ввели в компьютер, ничего кроме чисел, которые могут манипулировать со всеми возможностями арифметики и логики компьютера. Когда мы используем изображения как переменные, мы называем действия, выполняемые над ними, алгебраическими. Алгебраическое действие может быть одного из двух типов, точечное или матричное. Оба действия могут описываться следующим выражением:
X оператор Y = Z
X и Y может быть изображениями или скаляры (числа), и Z должен быть изображением. Действие точечное выполняется между каждым соответственным элементом X и Y. Вид матрицы действия более комплексен и содержит детальные серии шагов, которые будут обсуждаться позже. Мы делаем предположение, что как X, так и Y, если это изображения, имеют одно разрешение, или пространственную резолюцию. Выравнивание, как линейный процесс, иллюстрировано графически на рис. 3.1.
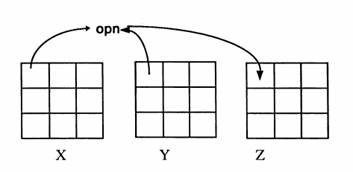
3.1 Линейные алгебраические действия над изображениями.
Отметим, что изображения представлены, как массив чисел, которые пространственно организуются в изображение такого же рода. Как пример линейного алгебраического действия, например, мы имеем два изображения того же места действия. В одном из изображений мы видим комнату, возможно помещение склада. В остальном изображении мы видим помещение склада с человеком. Если мы позволяем изображению запоминаться в глобальной переменной изображения X и остальному в Y, и мы предполагаем, что оператор - вычитание, то изображение Z - результат алгебраическое действие - это представление всего (черный) со значениями только в расположениях пикселя, которые были различны между X и Y. Мы можем также предположить, что переменные ряда (Number_of_Rows, Number_of_Columns) и столбца доступны также как глобальные переменные.
Рисунок 3.2 иллюстрирует результаты вычитания изображения, где второе изображение вычтено из первого.

3.2 Пример вычитания изображения.
Как дальнейший пример алгебры пикселя, рассматривается контроль яркости вашего монитора. Этот контроль масштабирует полную яркость показа соразмерно к его установке. Таким же образом, мы можем множить каждый пиксель в изображении константой, увеличивать или уменьшать значение и, соответственно, полную яркость изображения.
3.2 Арифметические Операции
Арифметические операции между изображениями включают дополнение, вычитание, умножение, и дивизию. Во всех случаях, мы заменяем оператор в следующем выражении желаемым действием:
X оператор Y = Z
Наш стандартный ряд значения пикселя составляет 0 - 255, значения, возможные в 1 байте данных. Если операционная продукция - число вне этого ряда, мы должны или масштабировать полный набор результата, или выполнить операцию транзакции, в которой отрицательные числа установлены к нулю и большие положительные установлены к 255. Ясно, самый простой подход - выполнять транзакцию. Вычитание изображения полезно для обнаружения отличий между последовательностями изображения того же места действия. Процесс часто используется для системы обнаружения движения.
3.3 Логические Операции
Логические операции - это операции, выполняемые над пикселями изображения. Стандартные логические операторы И, ИЛИ, и НЕ применены, поскольку они представлены с арифметическими операциями, обсуждаемыми выше. Комбинации этих действий дадут любую логическую функцию (NAND, NOR, XOR, IOR, и так далее), хотя больше всего в программах с действиями над изображением используется XOR из-за его понятного эффекта замаскирования. Логические операции самые легкие для понимания в терминах двумерных изображений. Так как двумерное изображение содержит только значения пикселя рисунка пером, бинарные операции будут иметь неотложную визуальную уместность. Примеры элементарных логических операций предоставлены на рис. 3.3.
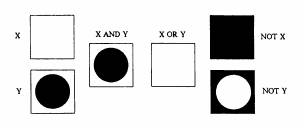
Рисунок 3.3 Логические операции на двумерных изображениях.
3.4 Действия с матрицами
Много изображающих методов требуют, что с изображением работали как с матрицей. В предыдущих главах мы применили действия пикселя к соответствию пикселя в выравнивании изображения. Если действие - это дополнение или вычитание, действия над матрицами идентичны.
Однако, если действие - это умножение, метод, обсуждаемый в главе 3.2, назван точечным. Точечное действие часто используется, чтобы исправить проблемные ответы сенсорного массива, где изображение калибрования генерируется, каждое значение пикселя высчитано как фактор исправления умножения. Изображения, полученные с помощью датчика, могут умножаться на изображение калибрования, чтобы исключить или смягчить индивидуальные несходства пикселя и сделать изображение последовательным через все пиксели. Однако, при обсуждающемся действии над матрицей, умножение изображений обычно понимается как перекрестный продукт, или продукт вектора. Перекрестный продукт двух изображений существенно отличен от продукта точки и требует понимания умножения вектора. Придумайте вектор как существование единой вертикальной линии (вектор ряда) или горизонтального столбца (вектор столбца) изображения. Профилирование - это процесс рассмотрения или извлечения вектора от изображения. Умножение вектора ряда и вектора столбца приводит к скалярному числу. Причина этого в определении математики умножения вектора и мы не должны исследовать этого в дальнейшем. Важно только, что мы понимаем, как это сделано. Рассмотрим следующий пример:
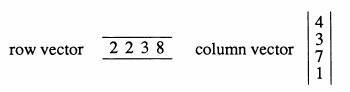
Для умножения вектора мы берем соответственные элементы каждого вектора, поскольку мы продвигаемся слева направо на векторе ряда и сверху вниз на векторе столбца. Мы тогда добавляем каждую из сумм, чтобы получить результат, который является (2 x 4) + (2 x 3) + (3 x7) + (8 x 1) = 43. Если мы желаем взять перекрестный продукт двух изображений, т.е., умножение матриц, мы умножаем каждый из векторов ряда первого изображения на каждый вектор столбца второго. Оба изображения должны иметь ту же пространственную резолюцию, или измерение, как горизонтально, так и вертикально. Если изображения составляют 4 к 4, то мы будем иметь 16 значений после вычислений, и эти значения - это пиксели результирующего изображения. Например

Первый ряд первого изображения умножаем на первый столбец второго изображения, чтобы получить первый элемент изображения результата от умножения вектора. Отметьте, что индекс для результата является [1, 1]. Индекс каждого элемента в изображении результата говорит нам, какая это пара ряда-столбца, чтобы получить значение для нужного пикселя. Чтобы получить значение [3, 4] пикселя, мы должны третий ряд первого изображения перемножить с четвертым столбцом второго изображения. Образец кода предоставлен функцией cross_multiply, которая перемножает два изображения. Функция имеет доступ к глобальным переменным матрицы, содержащим изображения (X и Y) и запоминающим результат (Z).