 ДонНТУ
ДонНТУ
 RUS
RUS
 Библиотека / Печатные издания
Библиотека / Печатные издания

Авторы: Докт. хим.наук Ю.М. Королев (ИНХС АН РФ) и канд. хим. наук С.Г.Гагарин (ИГИ)
Источник: Кокс и химия, 1996, №1, с. 6-10
РЕНТГЕНОГРАФИЧЕСКИЙ ФАЗОВЫЙ АНАЛИЗ ОРГАНИЧЕСКОЙ МАССЫ КАМЕННЫХ УГЛЕЙ
При исследовании многокомпонентных углеродистых систем особую роль приобретают такие прямые методы ,как, например, рентгенографический количественный фазовый анализ (РКФА). Этот метод позволяет наряду с уверенной диагностикой любого углеродистого компонента однозначно определять динамику и механизм фазовых преобразований природных или синтетических углеродистых систем в процессе воздействия на них различных физико-химических факторов. В частности, в работах [1, 2] рассмотрены вопросы динамики фазового преобразования органической массы угля в процессе метаморфизма.
В результате всестороннего рентгенофазового изучения природных и искусственных углеродистых веществ было установлено, что подавляющее большинство этих соединений относится к аморфным образованиям (3]. В частности, органическая составляющая каменных углей представляет собой смесь различных рентгеноаморфных компонентов, присутствие и количество которых меняется в ряду метаморфизма [1, 2].
Все угли, особенно на ранних и средних стадиях углефикации, нельзя отнести к чисто углеродистым веществам, поскольку для них характерно переменное отношение Н/С. Как было установлено в работе [1], в углях и антрацитах присутствуют четыре углеводородных и одна углеродная составляющая. Каждая из фаз характеризуется определенным значением главного межплоскостного расстояния, а профили и характер дифракционного спектра каждого компонента определяются строением слагающих данный компонент молекул, характером их взаимодействия в кристаллитах и размерами последних (областей когерентного рассеяния L).
 Типы аморфных систем и особенности их дифракционного рассеяния
Типы аморфных систем и особенности их дифракционного рассеяния

Если имеет место взаимодействие довольно однородных по составу и структуре молекул, то дифракционный спектр такого рентгеноаморфного вещества содержит три максимума. Первый (главный) рефлекс — самой большой интенсивности— соответствует межмолекулярному взаимодействию [4]. По полуширине этого максимума определяют высоту "стопки", в которую уложены молекулы, и при известной высоте молекулярного слоя подсчитывают их количество в упаковке. Межатомное расстояние d главного рефлекса отражает среднестатистическое расстояние между молекулами Я, которое определяется модифицированным уравнением Эренфеста [5]:
![]() (1)
(1)
Здесь θ — брэгговскии угол; λ — длина волны рентгеновского излучения.
Второе отражение, по интенсивности приблизительно в 10 раз меньшее, чем главное, отвечает внутримолекулярному взаимодействию. Для многих углеродистых веществ величина d этого рефлекса колеблется ( ~ 0,2 нм). По его полуширине можно определить средний диаметр молекул.
Наконец, третий рефлекс слабой интенсивности ( ~ 1 % от главного) соответствует межатомному взаимодействию С-С, С-Н, С=O и т.д., в связи с чем средняя величина d составляет от 0,11 до 014 нм. Типичным представителем подобной аморфной системы является оленекский богхед, дифракционный спектр и описание структуры которого приведены в публикациях [1, 4].
Для систем, состоящих из различных по составу и строению молекул, когерентное взаимодействие практически исключено; дифракция представлена одним широким (Δ = 15° θ) гало вследствие слияния двух нестрогих дифракционных эффектов от межмолекулярного и внутримолекулярного взаимодействий. В данном случае система обладает наибольшей степенью аморфности. (В качестве примера можно привести "промежуточную" фазу с d ≈ 0,3 нм (Δ = 16° θ), представляющую собой основной компонент органического вещества торфов, гумуса почв и бурых углей [1].) Особый случай — это объекты, состоящие из слоистых элементов структуры. Таким компонентом в гумусовых углях является графитоподобная фаза (аморфный графит), кристаллиты которой сложены из тех же сеток (с гексагональным мотивом и расстоянием С-С 0,141 нм), что и графиты. От кристаллических она сличается неупорядоченным смещением сеток в пюскрсти ab и малым размером областей когерентного рассеяния [1]). Так, в органическом веществе почв и торфов графитоподобный компонент обладает среднестатистическим размером Lc = 1,2 - 1,5 нм, тогда как даже в несовершенном графите эта величина достигает 25—30 нм [1].
Отмеченные элементы неупорядоченности в структуре графитоподобного компонента приводят к исчезновению пространственных рефлексов hkl, размытию и слиянию рефлексов, в результате чего образуются широкие полосы hk. Дифракционный спектр таких объектов представлен немногочисленными асимметричными рефлексами. При атом асимметричность, как будет показано, зависит от индекса отражений. Тем не менее, несмотря на размытый характер дифракции, положение рефлексов и соотношение их интенсивностей отвечают соответствующим отражениям графита, что подтверждают теоретические расчеты [6]. В процессе катагенеза происходит постепенное совершенствование кристаллической структуры графитоподобной фазы, в результате чего величина Lc постепенно увеличивается: с 1,2 нм в гумусе почв, торфа и бурых углей до 4 нм для суперантрацитов [1].
 Интерпретация дифрактограмм и определение фазового состава органической массы углей
Интерпретация дифрактограмм и определение фазового состава органической массы углей

Дифракционный спектр углей представляет собой суперпозицию главных рефлексов нескольких рентгенографических фаз с широким разбросом значений d = 0,3-2 нм главного максимума. Поскольку рефлексы от этих фаз имеют довольно значительную полуширину (2—5° θ ), то они сливаются в один широкий максимум различной конфигурации в угловом интервале от 2 до 15° θ.
Для качественного и количественного анализов важно знать положение и интенсивность главных рефлексов каждого компонента. В тех случаях, когда дифрактометры лишены выхода на ЭВМ, разложение сложного дифракционного максимума на составляющие может быть осуществлено методом итераций с использованием аппроксимации экспериментальных профилей рефлексов.
В последнее время появились работы, в которых аппроксимацию реальных рефлексов от различных кристаллических объектов осуществляли с помощью ряда колоколообразных функций. При этом чаще всего аппроксимация успешнее выполнялась путем их комбинации. (Подробно вопрос рассмотрен в публикациях [7, 8].) Тщательный математический анализ ряда колоколообразных функций (Лоренца, модифицированного Лоренца, Гаусса, псевдо-Фойгта, Пирсона) показал, что экспериментальные профили отражений таких кристаллических объектов, как диоксид циркония, каолинит, диккит, аппроксимируются с высокой точностью с помощью суперпозиции двух гауссианов. Поэтому профиль рефлекса можно представить как результат сложения двух колоколообразных функций разной крутизны, причем полуширина Δ нижней части вдвое больше верхней.
При использовании РКФА для изучения углеродистых веществ разложение сложного максимума осуществляли с помощью итерационного метода. Суть его заключается в следующем [9].
Допустим, что дифракционное отражение Y(x) состоит из двух наложенных максимумов, профили которых описываются функциями соответственно
![]()
зависящими от угловой ширины Δ j:
![]() (2)
(2)
Условие (2) должно выполняться при правильном выборе величин Δj. На первом этапе разложения используем пробные значения Δ11 и Δ21, которые при подстановке в (2) и анализе отклонений суммы y11 + y21 от Y корректируются с получением Δ12 и Δ22. Эти оценки уточняем далее до Δ1i и Δ2i. (Здесь i — номер итерации.) Процесс подбора заканчивается при i = n, когда равенство (2) выполняется в пределах заданной точности в любой точке х спектра отражений.
Анализ обработанного многочисленного экспериментального материала показал, что профили всех углеводородных фаз описываются симметричными колоколообразными функциями типа гауссианов. Исключение составляет графитоподобная фаза, у которой профили рефлексов, как и у всякой слоистой системы [10—12], асимметричны и направленность пологого спада интенсивности зависит от индекса отражения.
На основании анализа профилей рефлекса 002 большого количества образцов антрацитов и технического углерода удалось установить, что коэффициент асимметрии КА= Δл/ Δп. (Здесь Δл и Δп — полуширины соответственно левой и правой частей рефлекса). КА варьирует в пределах 1,2—1,6 и в среднем составляет 1,4; близкое значение асимметричности (КА = 1,3) зафиксировано в работе [13].
Оценка погрешностей при использовании описанного метода показала, что ошибка в определении интенсивности рефлексов зависит от количества той или иной фазы в смеси. Так, при ее содержании >20 % относительная ошибка не превышает ±5 %. Получаемые таким образом значения межплоскостных расстояний d и интенсивности отражений использовали для идентификации фаз и определения их содержания, а также для получения некоторых других рентгенографических характеристик, например размеров областей когерентного рассеяния La, Lc и степени анизотропии [1, 3, 4].
 Компьютерный метод обработки дифракционных спектров
Компьютерный метод обработки дифракционных спектров

Описанный алгоритм анализа сложной дифракционной картины, наблюдаемой при рентгенофазовом исследовании структуры углей, положен в основу автоматизированного подбора параметров отдельных компонентов (рентгенографических фаз), обеспечивающих суммарно воспроизведение экспериментальных дифракционных спектров образцов. При этом методика подбора формально аналогична поиску кинетических констант при описании динамики преобразований структуры ОМУ (2) или при подгонке ИК-спектров по набору полос поглощения [14].
Теоретический дифракционный спектр представляется суммой N рефлексов, обязанных дифракции от N рентгенографических фаз:
![]() (3)
(3)
где Аj— интенсивность отражений для i-той фазы, описываемая колоколообразной функцией с параметрами θi (положение в угловой шкале) и Δi (полная ширина на половине высоты пика). Как уже отмечалось, в случае углеводородных фаз функции Аj (θi, Δi) представляют собой гауссианы:
![]() (4)
(4)
Здесь hi — высота пика; σi — среднеквадратическое отклонение, связанное с шириной пика соотношением σi = Δi /(2 · 1,177). Выражение Аj (θ) для графитоподобной фазы представлено составной функцией, включающей гауссианы нижней части полосы и верхней (главной) части рефлекса. Для нижней части:
![]() (5)
(5)
где σгр.1 относится к левой (широкой) и правой (узкой) компонентам гауссиана соответственно при θ<θгр.1 и θ> θ гр.1.
Аналогично для верхней части рефлекса:
![]() (6)
(6)
Отметим, что в выражениях (5) и (6) величина θгр одна и та же, характеризующая положение в шкале в общего рефлекса графитоподобной фазы. Возможность количественной передачи функциями (5) и (6) экспериментальных отражений 002, полученных описанным в предыдущем разделе методом, подтверждает обработка данных для ряда углей разных стадий метаморфизма (см. таблицу).
Марка угля |
Стадия графитизации по [1] |
Параметры компонент гауссиана |
|||||||
θгр |
hгр.2 |
а + b |
а/(а + b) |
h |
с + d |
с/(с+ d) |
h1+h2 |
||
Д |
К1 |
11,66 |
44.9 |
5,69 |
0,585 |
108,5 |
3,65 |
0,515 |
153,4 |
Г |
К2 |
12,17 |
50,6 |
5,11 |
0,661 |
126,2 |
2,64 |
0,553 |
176,8 |
Г |
КЗ |
12,25 |
34,9 |
5,52 |
0,559 |
130,9 |
2,85 |
0,594 |
165,8 |
Ж |
К4 |
12,38 |
50,9 |
4.91 |
0,519 |
126,8 |
2,53 |
0,607 |
177,7 |
К |
К4 |
12,55 |
43,1 |
3,44 |
0,594 |
137,9 |
2,20 |
0,600 |
181,0 |
к |
А1 |
12,64 |
79,1 |
4,07 |
0,616 |
106,0 |
2,19 |
0,510 |
185,1 |
А |
А4 |
12,77 |
39,8 |
4,57 |
0,627 |
159,5 |
1,69 |
0,627 |
199,3 |
А |
|
12,80 |
41,6 |
3,08 |
0,625 |
152,0 |
0,89 |
0,603 |
193,6 |
На рис.1 в качестве примера приведено разложение дифракционного максимума 002 графитоподобной фазы угля коксовой стадии К4 при θгр = 12,55°. Коэффициенты асимметрии составных гауссианов для нижней и верхней частей рефлекса можно определить из выражений (см.рис.1):
![]() (7)
(7)
Приведенные в таблице данные указывают на закономерное изменение параметров для компонент гауссиана в ряду метаморфизма угля: увеличивается брэгговский угол θгр и общая высота пика h1+h2, возрастает анизотропия и снижается ширина рефлекса. Тенденцию изменения последней (по компонентам составного гауссиана) иллюстрирует рис.2. Закономерности изменения параметров учитываются при проведении компьютерной обработки дифракционных спектров углей с уточнением параметров, оцениваемых вручную на первом этапе. Это позволяет организовать быстро сходящийся итерационный процесс, приводящий к количественному описанию сложной дифракционной картины для различных углей.
Пример компьютерной расшифровки спектра представлен на рис.3 (для длиннопламенного угля). Расхождения между теоретическими и экспериментальными профилями рефлексов в диапазоне углов θ = 2-3° не превышают 0,5 % от максимальной интенсивности (спектры визуально неотличимы). По окончании обработки спектров выполняют интегрирование по контурам рефлексов отдельных фаз, что необходимо для расчета рентгенофазового состава угля.
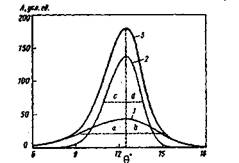
Рис.1. Построение рефлекса 002 графитоподобной фазы коксового угля на основе составных гауссианов нижней 1 и верхней частей рефлекса. Сумма гауссианов 3 совпадает с экспериментальным профилем при подборе полуширин: a, b и c, d соответственно для 1 и 2
Аналогичный подход применим и для анализа изменений структуры при различных воздействиях на угли.

Рис. 2. Зависимость угловой ширины d компонентов гауссианов для отражений 002 графитоподобной фазы от брэгговского угла θ . Компоненты: 1 — нижняя часть (2а); 2— верхняя часть (2с) рефлекса

Рис. 3. Разложение дифракционного спектра (линия без обозначения) длиннопламенного угля стадии графитизации К1 на фазовые компоненты с межплоскостными расстояниями d, нм: 1 - 0,983; 2 - 0.583; 3 - 0.382; 4 - 0.226
 Вывод
Вывод

Методика рентгенографического количественного фазового анализа органической массы углей и продуктов их переработки состоит из предварительного анализа углового распределения фаз и этапа - компьютерной обработки дифракционных спектров с определением параметров каждого фазового компонента и рентгенофазового состава изучаемого объекта. Получаемые результаты являются основой для разработки научных принципов оценки фазового состава и структурных параметров углей в целях совершенствования технологии переработки горючих ископаемых с рентгенографическим контролем при создании синтетических углеродистых веществ с заданными физико-химическими и механическими свойствами.
 Библиографический список
Библиографический список

1. Королев Ю.М. Рентгенографическое исследование гумусового органического вещества // ХТТ. 1989. № 6. С.11—19.
2. Гагарин С.Г., Королев Ю.М. Преобразование рентге-нофазовой структуры органической массы уг-ля...//Кокс и химия. 1994. №11. С.2—6.
3. Королев Ю.М., Моисеев ЮЛ., Попов В.Т. Рентгенографические критерии в установлении подобия фазового состава природных и искусственных углеродистых веществ//Накопление и преобразование органического вещества современных и ископаемых осадков; Сб.науч.ст. — М.: Наука, 1990. С.140—145.
4. Королев Ю.М. Рентгенографическое исследование органического вещества сапропелевого типа//Ге-ол.нефти и газа. 1989. № 9. С.50—53.
5. Voiglaeuder-Tetzner G.//Z.Phys. 1958. Bd 150. № 2. S.215—230.
6. Diamond RD.//Acta Cryst. 1957. V.10. P.359—364; 1958. V 11. P.129—138.
7. Новиков Г.Б., Егоров В.К., Соколов ЮЛ. Пирротины. — М.: Наука, 1988.— 185 с.
8. Чичагов А.В., Сипавина Л.В. Рентгенографические параметры твердых растворов. — М.: Наука, 1982. — 191 с.
9. Королев Ю.М. Итерационный метод разложения сложных дифракционных максимумов//Материалы XI Всес.совещ. по рентгенографии минерального сырья. — Свердловск: АН СССР. 1989. Т.1 С.41.
10. Warren B.FJIPhys. Rev. 1941. V.59. P.693—698
11. Biscoe J. Warren 8.F.//J.Appl.Phys. 1942. V.13. P.364—371
12. Brindley G.W., Mering J.//Acta Cryst. 1951. V.4. Р.441 — 447
13. Дубовик В.И., Носов Г.И., Четверикова О.П. Преобразование органического вещества пород.//ХТТ. 1976. № 5. С.94—101.
14. Гагарин С.Г., Гладун ТТ., Фриесен В.И., Микаэлан К.Г. Моделирование инфракрасных спектров мацералов.//Кокс и химия. 1993. № 4. С.6-9.