Разделы сайта

Авторы: Е.А. Беленков, Д.В. Яковлев

Источник: http://csc.ac.ru/news/2000_4/2000_4_4_3.pdf

ОСОБЕННОСТИ АНАЛИЗА ФОРМЫ ПРОФИЛЕЙ РЕНТГЕНОВСКИХ ДИФРАКЦИОННЫХ ЛИНИЙ УГЛЕРОДНЫХ МАТЕРИАЛОВ.
ЧАСТЬ II
СВЯЗЬ ФОРМЫ ПРОФИЛЕЙ И РАСПРЕДЕЛЕНИЯ КРИСТАЛЛОВ ПО РАЗМЕРАМ

Трудности применения методик рентгеноструктурного анализа для определения параметров кристаллической структуры углеродных материалов, по форме профилей рентгеновских дифракционных максимумов, обусловлены асимметрией профилей. Могут быть, две основные причины асимметрии дифракционных линий. Первой, причиной асимметрии может быть многофазность образца, тогда методика предварительной обработки должна заключаться в разделении дифракционных максимумов на компоненты соответствующие различным фазам. Однако, как показано в первой части данной статьи, такой способ анализа в большинстве случаев не имеет смысла [1]. Другая причина асимметрии может заключаться в непостоянстве межслоевых расстояний в кристаллах различного размера. Действительно для углеродных материалов экспериментально фиксируются зависимости межслоевых расстояний от размеров кристаллов [2—7] (рис. 1, 2). Поэтому целью данного исследования был анализ возможного влияния, зависимости межплоскостных расстояний от размеров кристаллов на форму рентгеновских дифракционных максимумов.

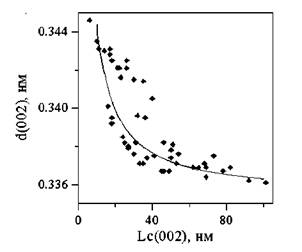
Рис. 1. Зависимость межплоскостных расстояний d₀₀₂ от средних размеров областей когерентного рассеяния Lc (из работы [3])

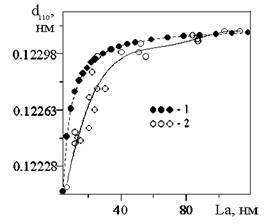
Рис. 2. Зависимость межплоскостных расстояний d₁₁₀ от средних размеров областей когерентного рассеяния La:
1 — расчетные точки; 2 — экспериментальные точки (из работы [4])

Суть моделирования профилей заключалась в расчете интенсивности рассеяния кристаллами модельных образцов. При этом предполагалось, что функция рассеяния отдельным кристаллом описывается функцией:

(1)

где N₁, N₂ и N₃ - количество периодов трансляций в соответствующих кристаллографических направлениях; h, k,i - индексы Миллера; F - структурная амплитуда [8]. Интенсивность рассеяния образцом рассчитывалась как сумма интенсивностей рассеяния отдельных кристаллов, составляющих образец.

Обработка получаемых в результате моделирования профилей дифракционных максимумов выполняли путем нахождения интегральной ширины (3 = I f(20)d₂₀/Imax , где 0 - угол дифракции, I max - максимальная интенсивность линии, f(20) - функция, описывающая форму дифракционного максимума, а затем путем расчета по формуле Селякова-Шеррера средних размеров областей когерентного рассеяния (ОКР) [8]. Получаемые в результате расчетов «экспериментальные» значения средних размеров ОКР Lэ сравнивали с истинными - изначально заданными.
Моделировались дифракционные максимумы 002 дисперсного графита для Cu Kа1 рентгеновского излучения (А, = 1,5405 A). Моделирование выполнялось для двух основных случаев: межслоевое расстояние d₀₀₂ = const (0,3354 нм) и d₀₀₂ - функция размеров кристаллов. Вид зависимости d₀₀₂ от размеров кристаллов в направлении кристаллографической оси «c» (Lс) был взят в виде формулы:

(2)

где значение коэффициента А = 0,0897504 нм² в которой было найдено методом наименьших квадратов по экспериментальным точкам из работы [3], приведенным на рис. 1.

Для случая d₀₀₂ = const было выполнено моделирование дифракционных максимумов 002, для гипотетических углеродных материалов, в которых кристаллы распределены по размерам в соответствии с четырьмя основными типами распределения (рис. 3). (A) — Все кристаллы одного размера L₀ ;
(B) - размеры кристаллов находятся в диапазоне от L₀-ΔL до L₀+ΔL; вероятность найти кристаллы разного размера одинакова;
(C) - размеры кристаллов находятся в диапазоне от 0 до 2L₀; вероятность найти кристаллы разного размера монотонно увеличивается с ростом размеров кристаллов до L₀, а затем симметрично уменьшается (грубый аналог нормального распределения);
(D) - размеры кристаллов находятся в диапазоне от 0 до Lт; вероятность найти кристаллы разно- го размера монотонно увеличивается с ростом размеров кристаллов до L₀ (L₀= 0,666·Lт), а затем уменьшается (грубый аналог распределения Лифшица-Слезова [9]).

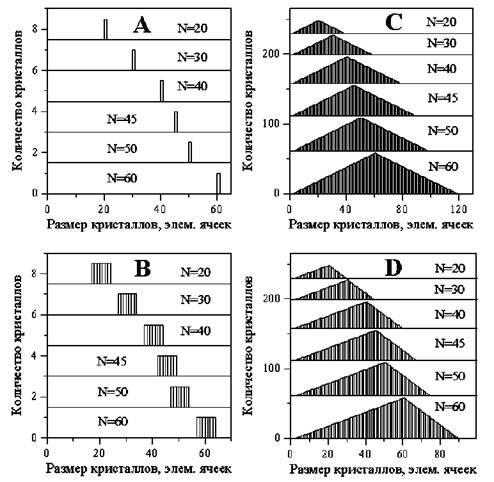
Рис. 3. Типы распределений кристаллов по размерам (A, B, C, D)

Расчеты проводили для случаев когда размер L₀ соответствовал кристаллам состоящим из N элементарных ячеек (N = 60; 50; 45; 40; 30; 20; что соответствовало размерам кристаллов L₀ = 40,248; 33,54; 30,186; 26,832; 20,124; 13,416 нм (табл. 1, 2)).
Для случая d₀₀₂ = const моделировались дифракционные максимумы 002 углеродных материалов состоящих из кристаллов распределение по размерам которых было (A), (B), (C) и (D) типов. Кроме того, было выполнено моделирование для распределения (E) типичного для каталитической графитации. В этом случае углеродные материалы состоят из смеси кристаллов малого размера (распределение D) и крупных кристаллов (размером 150 элементарных ячеек) (рис. 4). Так как присутствие в мелкокристаллическом углеродном материале катализатора (обычно Fe, Сr, S или других карбидообразующих примесей) приводит к образованию кристаллов графита в результате растворения в катализаторе неупорядоченного и мелкокристаллического углерода и последующей конденсации растворенного углерода в виде крупных кристаллов [10—13].

Таблица 1 - Средние размеры ОКР определенные по форме профилей модельных дифракционных максимумов (d₀₀₂=const)

N	L0, нм	LТ, нм		LЭ, нм
		Тип распределения		Тип распределения
		A, B, C	D	A	B	C	D
60	40,248	40,248	33,7636	40,2465	40,2919	46,5134	38,1192
50	33,540	33,540	28,1736	33,5386	33,5930	38,6887	31,7479
45	30,186	30,186	25,3821	30,1860	30,2449	34,7765	28,5674
40	26,832	26,832	22,5836	26,8308	26,8986	30,8645	25,3770
30	20,124	20,124	16,9936	20,1230	20,2131	23,0415	19,0071
20	13,416	13,416	11,4036	13,4152	13,5501	15,2214	12,6398

Таблица 2 - Средние размеры ОКР определенные по форме профилей модельных дифракционных максимумов (d₀₀₂≠const)

 

 

N	L0, нм	L т, нм			Lэ, нм
		Тип распределения			Тип распределения
		A, B, C	D	E	A	B	C	D	E
60	40,248	40,248	33,7636	35,2660	40,4650	40,0797	31,4692	28,5873	26,7448
50	33,540	33,540	28,1736	30,1316	33,9804	33,6523	26,4098	24,0149	21,8751
45	30,186	30,186	25,3821	27,6445	30,7175	30,3202	23,9120	21,6239	19,2985
40	26,832	26,832	22,5836	25,2289	27,2592	26,8643	21,2917	19,3461	16,7009
30	20,124	20,124	16,9936	20,7948	20,6477	20,0806	16,1272	14,7068	23,1754
20	13,416	13,416	11,4036	17,5565	13,9587	13,1418	10,9278	10,0511	41,2194

Рис. 4. Распределение кристаллов по размерам (E), соответствующее каталитической графитации

Результаты расчетов для случая d₀₀₂ = const приведены на рис. 5 и в табл. 1. Профили линий для всех исследованных функций распределения симметричные (рис. 5). Однако размеры ОКР, определяемые по форме таких дифракционных линий, соответствуют теоретическим (изначально заданным) только для распределений (A) и (B) (табл. 1). Для распределения (C) средние размеры ОКР определяемые по интегральной ширине модельных дифракционных максимумов Lэ превышают изначально заданные L т на 13,5—15,5 %. В случае распределения (D) Lэ > Lт на 10—11,5 %.

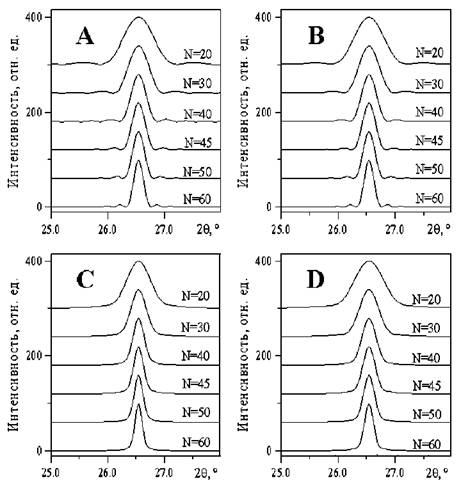
Рис. 5. Расчетные профили рентгеновских дифракционных максимумов 002 углеродных материалов, состоящих из кристаллов различного размера, соответствующие распределениям приведенным на рис. 3 (для d₀₀₂ = const)

Для случая d₀₀₂ = const получаемые в результате профили дифракционных линий симметричны только для распределения типа (А), профили максимумов для распределений (В), (С), (D) и (E) асимметричны (рис. 6). Форма дифракционных максимумов зависит от вида функции распределения кристаллов по размерам. Действительно если функция распределения кристаллов по размерам бимодальна, то бимодальны и сами дифракционные максимумы (рис. 6). Расчет средних размеров ОКР, по интегральной ширине таких дифракционных линий, дает результаты соответствующие изначально заданным средним размерам ОКР только в случае распределений (А) и (В) (табл. 2). Для распределений типа (С) и (D) Lэ на 18,5—22 % и 12—15 % меньше Lт . В случае распределения типа (E) средние размеры ОКР определяемые по дифракционным максимумам могут быть как меньше, так и больше истинных размеров (табл. 2), причем расхождение может быть очень большим до 134 % (N = 20).

Рис. 6. Расчетные профили рентгеновских дифракционных максимумов 002 углеродных материалов, состоящих из кристаллов различного размера, соответствующие распределениям приведенным на рис. 3, 4 (для d₀₀₂ ≠ const), а также экспериментальные профили 002 нефтяного кокса, содержавшего в исходном состоянии 2,5 мас. % серы и термообработанного при различных температурах (Т)

Насколько выполненные модельные расчеты отражают действительное устройство углеродных материалов можно проверить, сравнивая расчетные профили и экспериментально полученные. Например, на рис. 6, кроме модельных профилей приведены дифракционные максимумы 002 нефтяного кокса с примесью 2,5 мас. % серы, прошедшего термообработку в диапазоне температур 1400—2200 °С. В таком материале протекает каталитическая графита-ция в результате чего он состоит из мелкокристаллического углерода (размеры ОКР 2—20 нм) и графита имеющего размеры ОКР более 80—100 нм [11—12]. Экспериментальные дифракционные максимумы хорошо соответствуют расчетным как раз для бимодального распределения типа (E).
Таким образом, установлено, что асимметрия формы профилей дифракционных максимумов обусловлена зависимостью межплоскостных расстояний в углеродных материалах от размеров кристаллов. Форма профилей зависит от вида функции распределения кристаллов по размерам, поэтому правильный анализ формы профилей дифракционных линий УГМ должен заключаться в получении функции распределения кристаллов по размерам.
Однако корректное выполнение такого анализа встречается со значительными трудностями, так как для его выполнения необходимо изначально знать функцию описывающую зависимость межплоскостных расстояний от размеров ОКР. Использование экспериментальных зависимостей не совсем обосновано (рис. 1, 2), так как они были получены традиционными методами, результаты получаемыми которыми могут быть приняты лишь как первое грубое приближение. Для корректного анализа необходимо теоретическое определение вида функциональных зависимостей. Выполненные в работах [4, 6, 7, 14] исследования позволили определить теоретический вид зависимостей межплоскостных расстояний в углеродных материалах от размеров ОКР La (рис. 2). Для межслоевых расстояний с индексами hk0 теоретическая зависимость хорошо соответствует экспериментальной, что дает возможность определять распределение кристаллов по размерам по форме таких дифракционных максимумов в соответствии с методикой предложенной в [15]. При этом необходимо учитывать, что вид функциональной зависимости зависит от наличия текстуры на микроуровне (крайние случаи нефтяные коксы и углеродные волокна — отсутствие и наличие нанотекстуры соответственно).
К сожалению для дифракционных линий 00! ситуация более сложная — полученные модельные зависимости d₀₀₂ от La имеют ход аналогичный экспериментальным, однако наблюдается значительное расхождение в абсолютных значениях межслоевого расстояния, соответствующего кристаллам разного размера [7]. Кроме того необходимо теоретическое определение зависимости d₀₀₂ от Lс , которую конечно можно найти из d₀₀₂ = f(Lа) если найти функциональную взаимосвязь между Lс и La. Определение теоретических функциональной зависимости между размерами ОКР в кристаллографических направлениях «a» и «b» выполнялось, однако оказалось, что соотношение размеров в реальных углеродных материалах далеко от теоретически рассчитанного, энергетически выгодного [5]. Поэтому решать задачу нахождения функции распределения кристаллов по размерам по форме дифракционных максимумов 001 углеродных материалов необходимо методом последовательных приближений используя на первом шаге эмпирическую функциональную зависимость (1), затем определяя распределение кристаллов по размерам для реальных образцов и рассчитывая далее средние размеры ОКР можно получить функциональную зависимость d₀₀₂ = f(Lс ) для второго шага, затем повторить расчеты для новой функциональной зависимости и т. д.

1. Беленков Е.А. Особенности анализа формы профилей рентгеновских дифракционных линий углеродных материалов. Часть 1. Разделение на компоненты // Известия Челябинского Научного Центра. — 2001. — № 1. — С. 68—73.
2. Шулепов С.В. Физика углеграфитовых материалов. — М.: Металлургия, 1990. — 336 с.
3. Iwashita N., Inagaki M. Relations Between Structural Parameters Obtained by X–Ray Powder Diffraction of Various Carbon Materials // Carbon. — 1993. — Vol. 31, No7. — Р. 1107—1113.
4. Беленков Е.А., Карнаухов Е.А. Влияние размеров кристаллов на межатомные расстояния в дисперсном углероде // Физика твердого тела. — 1999. — № 4. — С. 744—747.
5. Беленков Е.А. Взаимосвязь структурных параметров углеродного волокна на основе поли-акрилонитрила // Журнал прикладной химии. — 1999. — Т. 72, вып. 9. — С. 1526—1530.
6. Беленков Е.А. Моделирование процесса формирования кристаллической структуры углеродного волокна // Кристаллография. — 1999. — Т. 44, № 5. — С. 808—813.
7. Беленков Е.А. Моделирование структурных превращений в кристаллах углеродных материалов, обусловленных изменением их размеров // Известия Челябинского Научного Центра. — 2000. — № 2. — С. 42—49.
8. Уманский Я.С., Скаков Ю.А., Иванов А.Н., Расторгуев Л.Н. Кристаллография, рентгенография и электронная микроскопия. — М.: Металлургия, 1982. — 632 с.
9. Лифшиц И.М., Слезов В.В. О кинетике диффузионного распада пересыщенных твердых растворов // ЖЭТФ. — 1958. — Т. 35, вып. 2. — С. 479—487.
10. Fitzer E., Weisenburger S. Evidence of Catalytic Effect of Sulphur on Graphitization Between 1400 °C and 2000 °C // Carbon. — 1976. — Vol. — 14. — Р. 195—198.
11. Беленков Е.А., Тюменцев В.А., Фотиев А.А. Особенность перехода содержащего серу углерода в графит // Неорганические материалы. — 1995. — Т. 31, № 5. — С. 651—654.
12. Tyumentsev V.A., Belenkov E.A., Shveikin G.P., Podkopaev S.A. The Effect of Sulfur and Other Impurities on Carbon–Graphite Transition // Carbon. — 1998. — Vol. 36, No 7—8. — Р. 845—853.
13. Криворучко О.П., Зайковский В.И. Образование жидкой фазы в системе углерод–металл при необычайно низкой температуре // Кинетика и катализ. — 1998. — Т. 39, № 4. — С. 607—617.
14. Беленков Е.А. Взаимосвязь межатомных расстояний и размеров кристаллов в дисперсном углероде // Известия Челябинского Научного Центра. — 1999. — № 2. — С. 27—32.
15. Беленков Е.А. Нахождение функции распределения кристаллов по размерам по форме рентгеновских дифракционных линий // XIV Международное совещание по рентгенографии минералов: Тезисы докладов. — 1999. — С. 282—283.