Задача логистики закупок и управления запасами
заключается в бесперебойном обеспечении предприятия
материальными ресурсами, отвечающими установленным
стандартам качества, с наименьшими общими затратами и
издержками на движение материалопотока включающими:
номинальную цену, затраты на доставку, расходы на
содержание запасов и иные выигрыши и потери. Одним из
важных инструментов оптимизации управления запасами
является расчёт оптимального размера поставки. А среди
моделей расчёта особо выделяется формула Вильсона,
которую также часто называют формулой оптимального
размера заказа или формулой экономичного размера заказа
(Economic order quantity - EOQ).
Многие специалисты по логистике и преподаватели
логистики считают формулу Вильсона простой, популярной,
но сами нередко отказываются от её применения, указывая
ту причину, что эта формула имеет ряд серьёзных
ограничений и допущений. Допущения для формулы
оптимального размера поставки EOQ следующие:
- расход ресурсов непрерывный и равномерный;
- период между двумя смежными поставками постоянен;
- спрос удовлетворяется полностью и мгновенно;
- транзитный и страховой запасы отсутствуют;
- ёмкость склада не ограничена;
- затраты на размещение и выполнение заказа не
зависят от размера заказа и постоянные в течение
планового периода;
- цена поставляемой продукции в течение планового
периода постоянная;
- затраты на содержание запаса единицы продукции в
течение единицы времени постоянные и не зависит от
суммы вложенных в запасы средств и сроков.
Приведённые выше допущения накладывают много
ограничений практического характера, без которых
достоверность расчётов по данной формуле вызывает
серьёзные сомнения.
Для преодоления некоторых ограничений предпринимались
попытки изменить алгоритм расчётов. С изменением
алгоритма стал возможен анализ системы скидок, вариант
формулы с пополнением запасов в течение некоторого
времени, расчёт размера поставки в преддверии ожидаемого
повышения цен на закупаемый товар.
Однако без ответа остаются многие вопросы и среди них
следующие: как рассчитать размер заказа, если доставку
осуществляет поставщик и стоимость доставки включена в
цену товара, как учесть наличие страховых запасов на
складе, использовать ли в расчётах цену материалов с
налогом на добавленную стоимость (НДС) или без НДС и
т.п. Эти и тому подобные практические вопросы могут
поставить специалиста по логистике в тупик, усомниться в
действенности модели и отказаться от применения
основного инструмента оптимизации поставок.
Возможность применения модификаций формулы Вильсона
для случаев, когда пополнение запасов осуществляется не
мгновенно, а за определённый промежуток времени, для
случаев предоставления системы скидок в зависимости от
объёмов поставки и для случаев ожидаемого повышения цены
на ресурсы достаточно известны, их описание можно найти
во многих источниках. В данной статье они будут
исключены из рассмотрения, но рассмотрим следующие три:
влияние страховых запасов на расчёт оптимального размера
поставки, уточнение переменных расходов, связанных с
содержанием запасов и решение вопроса об используемой
цене материальных ресурсов.
Для начала рассмотрим, как получена формула Вильсона
(EOQ - Economic order quantity). Со стандартными
условиями и ограничениями она имеет следующий вид:
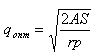
Обозначения: A - затраты на размещение и
выполнение заказа; S - годовая потребность в
ресурсах; q - размер единовременной поставки;
r - процентная ставка на хранение ресурсов
(ставка дисконтирования); p - цена единицы
закупаемых ресурсов.
Но для того чтобы разобраться в возможностях и
ограничениях формулы EOQ надо знать её природу.
Определение экономического размера заказа на поставку
товара основано на минимизации общей стоимости двух
видов затрат: затрат на хранение запасов, прямо
пропорциональных размеру заказа и затрат на размещение
заказа.
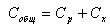
Обозначения следующие Собщ -
суммарные затраты за определённый период времени (для
упрощения расчётов, период времени обычно принимается
равным одному году); Ср - затраты на
размещение заказа; Сх - затраты на
хранение ресурсов.
Общие расходы на материальный поток определяются по
следующей известной формуле:
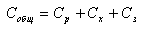
Обозначения следующие: Сз - затраты
на закупку ресурсов. В развернутом виде формула будет
следующей:

Оптимальный размер поставки может быть найден с
помощью метода исследования функции, поиска её
экстремума. Если указанную формулу суммарных затрат
принять за функцию и последовательно изменять размер
поставки q, то оптимальный размер поставки будет
соответствовать минимальному значению суммарных затрат.
С другой стороны, функция суммарных затрат является
непрерывной и дифференцируемой на интервале (0;
inf). Задача определения оптимального размера
поставки, соответствующего минимальным суммарным
затратам, заключается в поиске минимального значения
функции путём исследования. Минимальное значение
находится в точке её экстремума. Исследуем функцию на
указанном интервале. Если продифференцировать её по
q, то производная функции будет следующей:
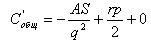
Для того чтобы утверждать о нахождении экстремальной
точки, первая производная функции должна иметь решение,
а точка, в которой первая производная равна нулю, должна
быть стационарной. Формула имеет следующий вид:

Соответственно точка экстремума функции, минимум
затрат и оптимальный размер поставки будут находиться в
точке qопт. Решая уравнение
относительно q, получим:
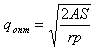
Это и есть формула оптимального размера заказа
(Economic order quantity) - формула Вильсона.
Математический вывод формулы Вильсона важен для
понимания некоторых её возможностей и ограничений. А
понимание нужно, для того чтобы исключить ошибки,
возможные при попытках практического применения
расширенных возможностей, которые предоставляет эта
формула.
Главный вывод, касающийся ограничений использования
формулы EOQ, заключён в том, что функция затрат должна
быть непрерывной и дифференцируемой на интервале (0;
inf). Соответственно задача нахождения оптимального
размера поставки будет решаться за один шаг. Изменение
алгоритма расчёта, например для анализа системы скидок,
приводит к тому, что в функции суммарных затрат
появляются точки разрыва первого рода. Формально такая
функция не подлежит дифференцированию. Решение задачи
заключается в поиске минимальных значений суммарных
затрат на каждом из интервалов между точками разрыва и в
самих точках. Но этот метод уже будет называться не
исследованием функции, а методом перебора значений.
Вариантов же, которые нужно посчитать и сравнить между
собой, будет ровно столько, сколько будет комбинаций
самих параметров в формуле суммарных затрат.
1. Страховые запасы.
Очень часто отсутствие страховых запасов в модели EOQ
считается как одно из ограничений в её использовании.
Указывается, что формула Вильсона рассчитана на случай
моментального пополнения, без страховых запасов. Что же
реально происходит со страховыми запасами? Какое влияние
они оказывают на расчёт оптимального размера заказа?
Расходы на содержание страховых запасов равны
произведению величины страховых запасов на цену единицы
ресурсов и на процентную ставку расходов на их
содержание:
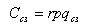
В формулу суммарных затрат введём расходы на
содержание страховых запасов. Формула будет следующей:

qсз - количество страховых запасов.
Произведение r*p*qсз является
константой. Заметим ещё раз, что q и
qсз - это разные параметры, изменение
размера поставки q не влияет на величину
страховых запасов qсз. Поэтому при
дифференцировании функции по q это произведение
превратится в ноль, и мы получим следующую формулу:

Дальнейшие преобразования полученного уравнения
приведут нас опять к формуле EOQ.

Очевидно, что использование величины страховых
запасов в расчётах суммарных затрат ни как не влияет на
формулу оптимального размера поставки.
Данный вывод, тем не менее, не означает полную
бесполезность величины страховых запасов в формуле
суммарных затрат, их использование будет описано ниже,
при использовании данной формулы для выбора поставщика.
2. Расходы на содержание запасов.
В книгах можно встретить два вида формулы
оптимального размера поставки. Однако формулы приводятся
без подробного толкования по их содержанию и
особенностям применения:

В первом случае параметр r - обозначается как
процентная ставка и умножается на цену единицы товара,
измеряется, соответственно, в процентах, во втором
случае r - это издержки хранения единицы товара,
измеряемые в денежных величинах.
В реальности произведение цены ресурса на процентную
ставку более применимо, если рассматриваются только
расходы на связанный капитал, а показатель расходов на
единицу ресурса, если рассматриваются затраты на
хранение, причём затраты на хранение должны быть условно
переменными, то есть зависеть от количества хранимых
материальных ресурсов.
На самом же деле издержки могут включать как расход
на связанный капитал, так и условно - переменные расходы
на хранение. Соответственно первые расходы будут равны
произведению цены товара на ставку дисконтирования, а
вторые - это затраты на хранение единицы товара на
складах.
Таким образом, обе формулы имеют недостатки. Первая
формула учитывает только финансовые расходы на связанный
в запасах капитал и не учитывает складские расходы на
хранение. Вторая формула, напротив, учитывает только
расходы на хранение ресурсов на складе, но не учитывает
расходы, связанные с отвлечением финансовых средств.
Решение данной проблемы заключено в объединении тех и
других видов расходов в одной формуле. Поэтому
желательно рассматривать расходы на содержание запасов,
разделив их на составляющие части, по следующей формуле:
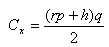
Где r*p - затраты на связанный капитал единицы
ресурса, а h - затраты на хранение на складе
единицы ресурса. Развёрнутая формула суммарных затрат
будет следующей:
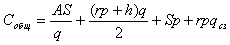
И соответственно формула расчёта оптимального размера
поставки, после преобразований, будет иметь вид:
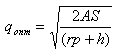
3. НДС в формуле EOQ.
Ещё одним является вопрос о применении цены и НДС в
формуле EOQ. Должна ли цена единицы ресурсов применяться
в расчётах оптимального размера поставки с НДС или без
НДС? Вопрос обычно появляется при обсуждении и
утверждении методологии и инструментов оптимизации
управления запасами. Причём этот вопрос обычно возникает
в экономических и финансовых службах, а не у закупщиков.
Подразделения закупа сталкиваются обычно с одной ценой -
той, которую нужно уплатить поставщику. А в финансовом
планировании и бюджетировании применяются оба вида цен.
Например, цена с НДС используется в бюджете движения
денежных средств, а цена без НДС - в экономических
расчётах себестоимости продукции и в бюджете доходов и
расходов. С одной стороны НДС подлежит уплате поставщику
и вроде бы должен участвовать в расчётах, с другой
стороны, согласно Налоговому Кодексу РФ, НДС подлежит
возмещению и не является расходом, а в описании
параметров формулы есть слова "затраты" и "расходы". В
книгах упоминания этой проблемы нет.
В данной формуле цена служит для определения расходов
на связанный капитал. То есть считаются деньги,
потраченные на выполнение заказа (доставку партии),
деньги, потраченные на приобретение (вложенные в запасы)
и деньги, потраченные на содержание запасов.
Расчёт расходов на связанный капитал, при содержании
запасов, должен учитывать денежные суммы, отвлечённые из
оборота в связи с приобретением ресурсов. Поэтому,
поскольку, поставщику мы выплачиваем денежную сумму по
цене товара с НДС, то и в формуле, соответственно мы
должны использовать цену товара с НДС. Для удобства, в
формуле, при расчёте, цена единицы ресурсов будет
использоваться без НДС (p), а НДС будет учтён в виде
коэффициента (rНДС), соответствующего
налоговой ставке:
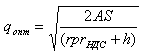
Для случая, если ставка НДС составляет 20% -
коэффициент rНДС будет равен 1,2, если ставка НДС
составляет 10%, то коэффициент rНДС будет
равен 1,1 и если приобретаемые материальные ресурсы не
облагаются НДС, то есть ставка НДС составляет 0%, то
коэффициент rНДС будет равен 1,0.
По законодательству РФ, НДС, уплаченный поставщику,
подлежит возмещению. Но возмещение возможно не ранее,
чем от покупателя будет получена оплата за готовую
продукцию. Можно предположить, что данная формула
справедлива только для случаев, когда возмещение НДС
осуществляется после использования ресурсов в
производстве, причём эти случаи являются типичными в
российской практике. Но с другой стороны, если
рассматривать оптимизацию управления и сырьевыми
запасами и запасами готовой продукции в целом, то уплата
НДС должна относиться к задаче оптимизации затрат на
входной материальный поток. Возмещение же НДС является
задачей оптимизации затрат выходящего потока. Потому
можно считать, что дополнительные финансовые расходы,
связанные с отвлечением средств в НДС, при приобретении
материальных ресурсов должны учитываться от момента
оплаты до момента расхода ресурсов в производство.
При необходимости использования формулы суммарных
затрат условие применения цены с НДС распространяется и
на расчёт расходов на содержание страховых запасов с той
же предпосылкой, что на их приобретение были выплачены
суммы, включающие как номинальную цену, так и НДС. Но
затраты на собственно приобретение материалов
(Сз) должны включать цену без НДС, именно
потому что НДС не включается в цену ресурсов, а подлежит
последующему возмещению:

Эти условия расчётов могут быть распространены и на
другие виды налогов или акцизов, сопровождающих
приобретение материальных ресурсов и влияющих на
правильность расчёта приведённой цены.
4. Выбор поставщика.
Рассмотрим вопрос, связанный с одним из вариантов
использования формулы Вильсона. С помощью формулы EOQ
возможно решение задачи выбора одного из нескольких
предложений поставщиков.
Каждое предложение может иметь от других предложений
следующие отличия:
- цене (система скидок);
- условия оплаты;
- затраты на доставку; и кроме того,
- под разных поставщиков могут резервироваться
различные объёмы страховых запасов, которые влияют на
величину связанного капитала и расходов на него.
Формула позволяет провести оценку, в денежном
выражении, предложений поставщиков по критерию
наименьших суммарных затрат.
Задача решается в три этапа. На первом этапе на
основе заданных условий, по формуле EOQ, определяется
оптимальный размер поставки для каждого поставщика. На
втором этапе по формуле суммарных затрат определяются
суммарные затраты по каждому предложению, при условии
включения в эту формулу соответствующего оптимального
размера поставки. На третьем этапе выбирается
предложение поставщика с наименьшими суммарными
затратами и соответствующим размером поставки.
Формула суммарных затрат примет вид:

Кроме того, в практике есть случаи, когда доставку
ресурсов осуществляет поставщик и затраты на доставку
уже включены в цену. Если за затраты на размещение и
выполнение заказа принять только транспортные расходы
(что обычно происходит, во-первых, по причине,
невозможности точного определения административных и
прочих расходов, сопровождающих размещение заказа, а
во-вторых, по причине пренебрежения этими расходами
из-за их малой величины по отношению к затратам на
доставку), то оптимальный размер поставки будет равен
нулю. Следовательно, формула EOQ не может дать верный
ответ. Если же кроме транспортных расходов в расчёте
используются прочие расходы, то величина оптимального
размера поставки всё равно может быть близкой к нулю или
не большой. На наше предложение поставщик вряд ли
согласится осуществлять ежедневный подвоз ресурсов, если
объём поставки составляет небольшую долю от вместимости
транспортного средства, увеличивая тем самым его
транспортные расходы. Решение данной проблемы
заключается в согласовании с поставщиком минимального
размера поставки, который тот готов осуществить за свой
счёт с включением затрат на доставку в цену ресурса,
либо пересмотром закупочной цены с переводом условия
доставки за счёт поставщика на доставку собственным
транспортом - самовывоз.
|