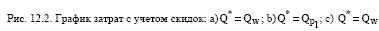Главная                                                                                                                                                              Библиотека   

                                                                                                               
Автор Т.В. Алесинская

Источник:
www.aup.ru/books/m84/uprz_emmm.pdf



Экономико-математические методы и модели


МОДЕЛЬ УПРАВЛЕНИЯ ЗАПАСАМИ, УЧИТЫВАЮЩАЯ СКИДКИ

1. Теоретическое введение
Уравнение общих затрат для ситуации, когда учитываются затраты на покупку товара, имеет вид:

Уравнение общих затрат

Риснок1 - Структура службы МТС предприятия

где с – цена товара [руб./ед. тов.];
   сv– затраты на покупку товара в единицу времени [руб./ед.t].
Если цена закупки складируемого товара постоянна и не зависит от Q, то ее включение в уравнение общих затрат приводит к перемещению графика этого уравнения параллельно оси Q и не изменяет его формы (см. рис. 12.1). Т.е. в случае постоянной цены товара ее учет не меняет оптимального решения Qw .

График затрат

Если на заказы большого объема предоставляются скидки, то заказы на более крупные партии повлекут за собой увеличение затрат на хранение, но это увеличение может быть компенсировано снижением закупочной цены. Таким образом, оптимальный размер заказа может изменяться по сравнению с ситуацией отсутствия скидок. Поэтому затраты на приобретение товара необходимо учитывать в модели покупок со скидками.

               Новые входные параметры модели, учитывающей скидки:
1) Qр1, Qр2 – точки разрыва цен, т.е. размеры покупок, при которых начинают действовать соответственно первая и вторая скидки, [ед. тов.];
2) с, с1, с2 – соответственно исходная цена, цена с первой скидкой, цена со второй скидкой, [руб./ед. тов.].

Влияние единственной скидки на общие затраты на УЗ показано на рис.12.2.

Чтобы определить оптимальный размер заказа Q*, необходимо проанализировать, в какую из трех областей попадает точка разрыва цены Qp1 (см. рис. 12.2).

Правило выбора Q* для случая с одной скидкой имеет вид:


2. Методические рекомендации

Правильность решения задач с УЗ со скидками в большой степени определяется качественно построенным графиком общих затрат с указанием на графике всех параметров, используемых при решении. Поэтому в первую очередь необходимо анализировать ситуацию графически и только после этого проводить численные вычисления. Например, если внимательно проанализировать ситуации на рис. 12.2, то можно принимать решение без непосредственного использования правила (12.2). Зрительно легко определить более "выгодный" объем заказа, найдя точку, координата которой по оси L лежит ниже других вариантов заказов.



При решении задач с двумя скидками сначала находится оптимальный объем заказа с учетом первой скидки, а затем рассматривается вторая скидка, т.е. обе подзадачи решаются по правилу (12.2).

Вверх