Peter Lammers, Uwe Küster

Abstract

We show performance results for the lattice Boltzmann method on three different architctures. The benchmarked architectures include an IBM Power5, the SGI Altix 3700 (LRZ Munich) and the NEC SX-8 (HLRS Stuttgart) respectively. The application used is the well known lattice Boltzmann solver BEST. Furthermore we use a modified lattice Boltzmann solver using a boundary-fitted cartesian mesh mesh to compare the performance of indirect addressing on the NEC SX-8 with the predecessor model SX-6.

Lattice Boltzmann Method

Nowadays the lattice Boltzmann method is applied to a wide range of scientific and and engineering disciplines including chemical and process engineering, bio and environmental processes and medical applications. Preferably it is used when highly complex geometries are involved. The first author of this artikle is intensively using the lattice Boltzmann method for simulations of flow control in wall bounded turbulence, turbulent drag reduction and control of transition [1]. Among chemical engineering the flow solver BEST was developed at the Lehrstuhl fur Stromungsmechanik (LSTM), Universitat Erlangen-Nurnberg for this purpose. Here, the BEST solver is used for most of the benchmarks their results are shown in this text. The benchmark itself (a plane channel) is motivated by wall bounded turbulence. The lattice Boltzmann method consists of a discretized kinetic equation for the one particle distribution function f,

for which an appropriate phase velocities lattice needs to be specified. In BEST, the 3D spatial cartesian grid is coupled to the D3Q19 streaming lattice [2] with 19 mesoscopic variables C,
is a relaxation parameter that determines the rate at which the particle interaction drives f to the equilibrium state f^eq. f^eq is appropriately chosen to satisfy the Navier-Stokes equation and depends on the hydrodynamic quantities like density, pressure and the velocity fields which are calculated from the moments of f.
In the benchmark codes, the algorithm is implemented just as given by eq. (1). That means a collision step (r.h.s) in which basically the equilibrium state function f^eq is calculated is followed by a propagation step (l.h.s) in which the mesoscopic variables f are streamed along the lattice directions C. In order to reduce the memory traffic both steps are combined. As the streaming step implicates a data dependency, it cannot be vectorized in a straightforward way. In the implementation this is by-passed by using two arrays of f for time step t and t+1 which are used in an alternating way. For cache based machines the inner loop of the main kernel is broken up in pieces. Especially the propagation step is done for pairs of the densities f.
For parallelization the overall spatial grid is block-wise distributed to the processors in BEST. At the boundaries, the propagating densities are first copied to a ghost layer and then sent to the adjacent processor block. The data exchange is realized by MPISendrecv which is at least the optimal choice on the SX network for this communication pattern. For more details of the implementation see [1] and [3].

Performance

In Figure 1, 2 and 3 the single and parallel performance of the algorithm implemented in BEST are shown for an IBM p575, an SGI Altix3700Bx2 and the NEC SX-8. The measurements on the Power5 are done by IBM [4]. In each case the CPU efficiency depending on the domain size per process is plotted. The efficiency is related to the peak performance (vector peak performance for the SX).
First we will look for the single processor performance given by the dotted black graphs first. The achievable performance per process of the Power5 CPU (Figure 1) is in the range between 16,5 and a maximum of 25 % efficiency. This corresponds to 1,25 and 1,9 GFlop/s. Significant outliers due to cache effects can be observed for inner loop lengths of 16, 24 and 32. The Itanium2 (Figure 2) achieves a maximum of 36 % efficiency corresponding to 2,3 GFlop/s. Performance drops significantly when the problem size exceeds the cache size. Further increasing the problem size, compiler-generated prefetching takes over and leads to gradual improvement up to a final level of 2,2 GFlop/s. In contrast, the performance of the vector system in Figure 3 increases with increasing vector length and saturates at an efficiency of close to 75 %, i.e. at a single processor application performance of 11,9 GFlop/s.
For the parallel scalability analysis we focus on weak-scaling scenarios. Here, ideal scalability means that all curves would collapse into one.

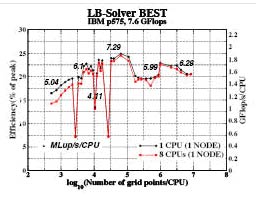
Figure 1:
Left: Efficiency, GFlop/s and MLup/s of the lattice Boltzmann solver BEST depending on the domain size and the number of processors for up to 8 CPUs of IBM p575

In Figure 1 the results for a node IBM p575 with 8 CPUs are available. In contrast to the Power4 (results not shown here) the p575 provides sufficient memory bandwidth inside one node now.
In the SGI Altix two processors have to share one memory connection. Consequently when using two processors single CPU performance drops to 1,29 GFlop/s. Prefetching is still important but not as efficient as for one processor. Further, in Figure 2 weak scaling results for up to 120 Itanium2 CPUs on an SGI Altix3700 are given and in Figure 3 the NEC SX-8 results with up to 576 CPUs. For the lattice Boltzmann application we see on the 576 processor NEC SX-8 system a maximum sustained performance of 5,7 TFlop/s. The same performance level would require at least 6400 Itanium2 CPUs on an SGI Altix3700. As seen in 3 the scalability of the NEC SX-8 system is not perfect. Parasitic non synchronous operating system processes show influences on aggregated waiting times. This effect becomes of course smaller by increasing per process system size. The load balancing itself is ideal for this benchmark case and can not cause any problems.

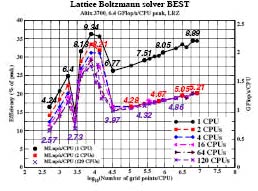
Figure 2:
Efficiency, GFlop/s and MLup/s of the lattice Boltzmann solver BEST depending on the domain size and the number of processors for up to 120 CPUs of a SGI Altix3700Bx2

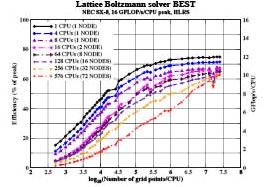
Figure 3:
Efficiency, and GFlop/s of the lattice Boltzmann solver BEST depending on the domain size and the ¬number of processors for up to 72 nodes 576 CPUs of a NEC SX-8

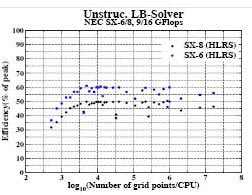
Figure 4:
Performance of an unstructured implementation of the lattice Boltzmann kernel on the SX-8 in comparison to the SX-6.

Finally we would like to focus in this context on the performance of indirect array addressing on the SX-8. In BEST the calculation is done on a block structured regular grid. But for highly complex geometries it is of course more appropriate to store only the cells inside the flow domain. For this, an index is needed to select the fluid cells and the information about adjacent nodes has to be stored in index lists.
In Figure 4 the performance on the SX-6 and 8 of such an implementation of the lattice Boltzmann method is plotted. The code used for the measurement is a collaborative development of the RRZE, the Institut fur Computeranwendungen im Bauingenieurwesen (CAB), Universitat Braunschweig, Section Computational Science, University of Amsterdam, Department of Medical Physics and Clinical Engineering, University of Sheffield, NEC CCRL and HLRS. The test cases are identical with the cases used for the previous plots.
Till now only a serial code version is available. This explains the slightly better performance for small grids. In the results shown so far, the communication dominates the calculation for small grids. The single CPU efficiency of the SX-6 is at a level of 60%. On the other hand the efficiency of the SX-8 is still 50% but 10% lower than on the SX-6. The reason is the higher memory latency of the recent system. Therefore it is more important on the SX-8 to prefetch the vector gather/scatter instructions for the indirect load/stores and hide the latency by other instructions. This can typically be done by unrolling simple loops. The present loop is complex enough for hiding these latencies partially.

Outlook

We too look forward to the performance of the new HLRB II system, an SGI Altix 4700. On this system the performance drop between one and two CPUs should not occur because of the better memory connection. It would also be interesting to have results for the IBM Blue Gene in Julich although this architecture is not aiming at flow simulations.

References

[1] Lammers, P.
Direkte numerische Simulationen wandgebundener Strömungen kleiner Reynoldszahlen mit dem lattice Boltzmann Verfahren. Dissertation, Universität Erlangen-Nürnberg (2005)

[2] Qian, Y.H., d’Humières, D., Lallemand, P.
Lattice BGK models for Navier-Stokes equation Europhysical Letter 17 (1992), 479-484

[3] Wellein, G., Zeiser, T., Hager, G., Donath, S. On the single processor performance of simple lattice Boltzmann kernels. Computers & Fluids (2005) in Press, corrected Proof, available online December 20, 2005

[4] Pichlmeier, J.
IBM, private communication (2005)

• Peter Lammers
• Uwe Küster

Höchstleistungsrechenzentrum Stuttgart, Germany.

Peter Lammers, Uwe Küster

Abstract

We show performance results for the lattice Boltzmann method on three different architctures. The benchmarked architectures include an IBM Power5, the SGI Altix 3700 (LRZ Munich) and the NEC SX-8 (HLRS Stuttgart) respectively. The application used is the well known lattice Boltzmann solver BEST. Furthermore we use a modified lattice Boltzmann solver using a boundary-fitted cartesian mesh mesh to compare the performance of indirect addressing on the NEC SX-8 with the predecessor model SX-6.

Lattice Boltzmann Method

Nowadays the lattice Boltzmann method is applied to a wide range of scientific and and engineering disciplines including chemical and process engineering, bio and environmental processes and medical applications. Preferably it is used when highly complex geometries are involved. The first author of this artikle is intensively using the lattice Boltzmann method for simulations of flow control in wall bounded turbulence, turbulent drag reduction and control of transition [1]. Among chemical engineering the flow solver BEST was developed at the Lehrstuhl fur Stromungsmechanik (LSTM), Universitat Erlangen-Nurnberg for this purpose. Here, the BEST solver is used for most of the benchmarks their results are shown in this text. The benchmark itself (a plane channel) is motivated by wall bounded turbulence. The lattice Boltzmann method consists of a discretized kinetic equation for the one particle distribution function f,

for which an appropriate phase velocities lattice needs to be specified. In BEST, the 3D spatial cartesian grid is coupled to the D3Q19 streaming lattice [2] with 19 mesoscopic variables C_α,τ, is a relaxation parameter that determines the rate at which the particle interaction drives f to the equilibrium state f^eq. f^eq is appropriately chosen to satisfy the Navier-Stokes equation and depends on the hydrodynamic quantities like density, pressure and the velocity fields which are calculated from the moments of f.
In the benchmark codes, the algorithm is implemented just as given by eq. (1). That means a collision step (r.h.s) in which basically the equilibrium state function f^eq is calculated is followed by a propagation step (l.h.s) in which the mesoscopic variables f_α are streamed along the lattice directions C_α. In order to reduce the memory traffic both steps are combined. As the streaming step implicates a data dependency, it cannot be vectorized in a straightforward way. In the implementation this is by-passed by using two arrays of f for time step t and t+1 which are used in an alternating way. For cache based machines the inner loop of the main kernel is broken up in pieces. Especially the propagation step is done for pairs of the densities f_α.
For parallelization the overall spatial grid is block-wise distributed to the processors in BEST. At the boundaries, the propagating densities are first copied to a ghost layer and then sent to the adjacent processor block. The data exchange is realized by MPISendrecv which is at least the optimal choice on the SX network for this communication pattern. For more details of the implementation see [1] and [3].

Performance

In Figure 1, 2 and 3 the single and parallel performance of the algorithm implemented in BEST are shown for an IBM p575, an SGI Altix3700Bx2 and the NEC SX-8. The measurements on the Power5 are done by IBM [4]. In each case the CPU efficiency depending on the domain size per process is plotted. The efficiency is related to the peak performance (vector peak performance for the SX).
First we will look for the single processor performance given by the dotted black graphs first. The achievable performance per process of the Power5 CPU (Figure 1) is in the range between 16,5 and a maximum of 25 % efficiency. This corresponds to 1,25 and 1,9 GFlop/s. Significant outliers due to cache effects can be observed for inner loop lengths of 16, 24 and 32. The Itanium2 (Figure 2) achieves a maximum of 36 % efficiency corresponding to 2,3 GFlop/s. Performance drops significantly when the problem size exceeds the cache size. Further increasing the problem size, compiler-generated prefetching takes over and leads to gradual improvement up to a final level of 2,2 GFlop/s. In contrast, the performance of the vector system in Figure 3 increases with increasing vector length and saturates at an efficiency of close to 75 %, i.e. at a single processor application performance of 11,9 GFlop/s.
For the parallel scalability analysis we focus on weak-scaling scenarios. Here, ideal scalability means that all curves would collapse into one.

Figure 1:
Left: Efficiency, GFlop/s and MLup/s of the lattice Boltzmann solver BEST depending on the domain size and the number of processors for up to 8 CPUs of IBM p575

In Figure 1 the results for a node IBM p575 with 8 CPUs are available. In contrast to the Power4 (results not shown here) the p575 provides sufficient memory bandwidth inside one node now. In the SGI Altix two processors have to share one memory connection. Consequently when using two processors single CPU performance drops to 1,29 GFlop/s. Prefetching is still important but not as efficient as for one processor. Further, in Figure 2 weak scaling results for up to 120 Itanium2 CPUs on an SGI Altix3700 are given and in Figure 3 the NEC SX-8 results with up to 576 CPUs. For the lattice Boltzmann application we see on the 576 processor NEC SX-8 system a maximum sustained performance of 5,7 TFlop/s. The same performance level would require at least 6400 Itanium2 CPUs on an SGI Altix3700. As seen in 3 the scalability of the NEC SX-8 system is not perfect. Parasitic non synchronous operating system processes show influences on aggregated waiting times. This effect becomes of course smaller by increasing per process system size. The load balancing itself is ideal for this benchmark case and can not cause any problems.

Figure 2:
Efficiency, GFlop/s and MLup/s of the lattice Boltzmann solver BEST depending on the domain size and the number of processors for up to 120 CPUs of a SGI Altix3700Bx2

Figure 3:
Efficiency, and GFlop/s of the lattice Boltzmann solver BEST depending on the domain size and the ¬number of processors for up to 72 nodes 576 CPUs of a NEC SX-8

Figure 4:
Performance of an unstructured implementation of the lattice Boltzmann kernel on the SX-8 in comparison to the SX-6.

Finally we would like to focus in this context on the performance of indirect array addressing on the SX-8. In BEST the calculation is done on a block structured regular grid. But for highly complex geometries it is of course more appropriate to store only the cells inside the flow domain. For this, an index is needed to select the fluid cells and the information about adjacent nodes has to be stored in index lists.
In Figure 4 the performance on the SX-6 and 8 of such an implementation of the lattice Boltzmann method is plotted. The code used for the measurement is a collaborative development of the RRZE, the Institut fur Computeranwendungen im Bauingenieurwesen (CAB), Universitat Braunschweig, Section Computational Science, University of Amsterdam, Department of Medical Physics and Clinical Engineering, University of Sheffield, NEC CCRL and HLRS. The test cases are identical with the cases used for the previous plots.
Till now only a serial code version is available. This explains the slightly better performance for small grids. In the results shown so far, the communication dominates the calculation for small grids. The single CPU efficiency of the SX-6 is at a level of 60%. On the other hand the efficiency of the SX-8 is still 50% but 10% lower than on the SX-6. The reason is the higher memory latency of the recent system. Therefore it is more important on the SX-8 to prefetch the vector gather/scatter instructions for the indirect load/stores and hide the latency by other instructions. This can typically be done by unrolling simple loops. The present loop is complex enough for hiding these latencies partially.

Outlook

We too look forward to the performance of the new HLRB II system, an SGI Altix 4700. On this system the performance drop between one and two CPUs should not occur because of the better memory connection. It would also be interesting to have results for the IBM Blue Gene in Julich although this architecture is not aiming at flow simulations.

References

[1] Lammers, P.
Direkte numerische Simulationen wandgebundener Strömungen kleiner Reynoldszahlen mit dem lattice Boltzmann Verfahren. Dissertation, Universität Erlangen-Nürnberg (2005)

[2] Qian, Y.H., d’Humières, D., Lallemand, P.
Lattice BGK models for Navier-Stokes equation Europhysical Letter 17 (1992), 479-484

[3] Wellein, G., Zeiser, T., Hager, G., Donath, S. On the single processor performance of simple lattice Boltzmann kernels. Computers & Fluids (2005) in Press, corrected Proof, available online December 20, 2005

[4] Pichlmeier, J.
IBM, private communication (2005)

• Peter Lammers
• Uwe Küster

Höchstleistungsrechenzentrum Stuttgart, Germany.