Peter Lammers, Uwe Küster

Введение

Мы представляем результаты быстродействия метода Больцмана на трех различных архитектурах. Данные эксперименты проводились на IBM Power5, SGI Altix 3700 (LRZ в Мюнхене) и NEC SX-8 (HLRS в Штуттгарте) соответственно. Используемое приложение – широко известный решатель метода Больцмана BEST. Кроме того, мы используем усовершенствованный решатель решеточного метода Больцмана с использованием гранично-совподающей декартовой сетки для того, чтобы сравнить быстродействие косвенной адресации на NEC SX-8 с предшествующей моделью SX-6.

Решеточный метод Больцмана

В настоящее время решеточный метод Больцмана применяется в обширной области научных и инженерных дисциплин, включая химическое и ехнологическое производство, биологические и экологические процессы, а также применение в медицине. Предпочтительнее использовать данный метод для конфигураций повышенной сложности. Первый из авторов данной статьи интенсивно использует решеточный метод Больцмана для моделирования контроля потока при ограниченной турбулентности, сокращения турбулентного аэродинамического сопротивления и контроля переходных процессов [1]. Кафедрой аэрогидромеханики (LSTM) университета Эрланген-Нюрнберг для химических отраслей был разработан решатель перемещения потоков воздуха BEST. В данной статье решатель BEST используется для тестирования на различных архитектурах, результаты которого представлены. Экспериментальная модель (плоский канал) была выбрана для обоснования ограничения турбулентности. Решеточный метод Больцмана состоит из дискретизированных кинетических уравнении одной функции распределения частицы f,

для которой должна быть определена соответствующая решетка скоростей фазы. В решателе BEST трехмерная пространственная декартовская сетка [2], подсоединенная к D3Q19 19-ю мезоскопическими переменными C,
, является параметром ослабления, определяющий скорость, с которой f приводит взаимодействующие элементарные частицы к состоянию равновесия f^eq. f^eq соответственно выбран таким образом, чтобы мог удовлетворить уравнению Навье-Стокса, и он зависит от гидродинамической величины как плотность, давление и поле скоростей, которые вычислены с моментов f.
В тестовых программах алгоритм реализован так, как представлено в уравнении (1). Это означает, что шаг столкновения (r.h.s), с которым в основном вычислена функция состояния равновесия f^eq сопровождается шагом распространения (l.h.s), с которым мезоскопические переменные f перемещются в направленнии решетки C. Для того, чтобы уменьшить количество обращений к памяти, оба шага объединяются. Поскольку на текущем шаге наблюдается зависимость данных между собой , векторизация не может осуществляться прямым способом. Для преодоления этого ограничения задействованы два массива f для шага времени t и t+1, которые используются попеременно. Для машин с кэш-памятью внутренний цикл главного ядра разбит на части. В частности, шаг распространения выполняется для пар плотностей f.
Для распараллеливания всей пространственной сетки в решателе BEST реализовано блочное распределение процессоров. На границах, перемноженные плотности копируются в буфер и затем пересылаются смежному процессорному блоку. Обмен данными осуществляются с помощью функций MPISendrecv, которые являются оптимальным вариантом для SX сети. Для получения более подробной информации о реализации данного метода смотрите [1] и [3].

Производительность

На рисунке 1, 2 и 3 представлена производительность алгоритма, последовательно и параллельно реализованного с помощью BEST на IBM p575, SGI Altix 3700Bx2 и NEC SX-8. Компания IBM [4] проводила опыты на машинах Power5. На каждом из рисунков представлена зависимость эффективности использования ЦП от размера области решетки, решаемой одним процессом. Эффективность же зависит от пиковой производительности (векторная пиковая производительность SX).
Сначала мы посмотрим на производительность одного процессора, на графике она изображена черным точками. Значения производительности достигаемой одним процессом Power5 CPU (рис 1) колеблется между 16,5% и максимальной отметкой 25%. Этим значениям соответствует 1,25 и 1,9 GFlop/s. Значительные скачки, возникающие из-за эффекта кэширования, наблюдаются для длин внутренних циклов длиной 16, 24 и 32.
Itanium2 достигает максимума эффективности в 36% , что соответствует 2,3 Gflops/s. Производительность значительно падает, в том случае, когда размерность задачи меньше размерности кэш-памяти. Затем при увеличении размерности задачи, вступает в действие произведенная компилятором предварительная выборка и приводит к постепенному увеличению производительности до заключительного уровня 2,2 GFlop/s. Для сравнения, производительность векторной системы на рис. 3 растет с увеличением длины вектора и доходит до отметки близкой к 75 %, то есть производительность одного процессора достигает 11,9 GFlop/s.
Для анализа масштабируемости при распараллеливании мы сосредотачиваемся на слабо масштабирующихся случаях. Здесь, идеальная масштабируемость означает то, что все кривые слились бы в одну.

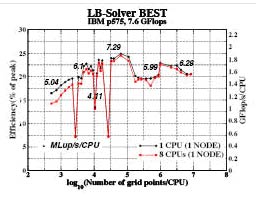
Рисунок 1 – Производительность, GFlop/s, MLup/s решателя решеточного метода Больцмана BEST в зависимости от размера области решетки, решаемой одним процессором, и количества процессоров от 1 до 8 CPUs IBM p575.

На рис. 1 представлены результаты для узла IBM p575 с 8 CPU. В сравнении с Power4 (результаты не приведены), р575 теперь обеспечивает достаточную пропускную способность памяти в одном узле.
В SGI Altix два процессора должны разделить одно соединение с памятью. Следовательно, в результате использования двумя процессорами одного CPU, производительность падает до 1,29 GFlop/s. Предварительная выборка по прежнему важна, но уже не так эффективна, как при работе одного процессора. Далее, на рис.2 представлены слабо масштабируемые результаты вплоть до 120 Itanium2 CPU на SGI Altix3700 и на рис.3 – результаты работы 576 CPU NEC SX-8. Мы видим, что при решении решеточного метода Больцмана на 576 процессорах системы NEC SX-8, устанавливается максимум производительности равный 5,7 TFlop/s. Аналогичный уровень производительности требовал-бы по крайней мере 6400 CPU Itanium2 на SGI Altix3700. На рис. 3 . как видно, масштабируемость системы NEC SX-8 не идеальна. Паразитные не синхронные процессы операционной системы приводят к ожиданию во времени. Этот эффект конечно уменьшается, при увеличении размера задачи, решаемой одним процессом. Балансировка нагрузки идеальна для данного случая и не может вызвать никаких проблем.

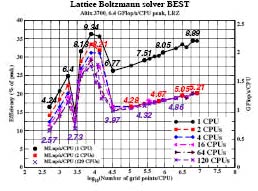
Рисунок 2 – Производительность, GFlop/s, MLup/s решателя решеточного метода Больцмана BEST в зависимости от размера области решетки, решаемой одним процессором, и количества процессоров вплоть 120 CPU SGI Altix3700Bx2.

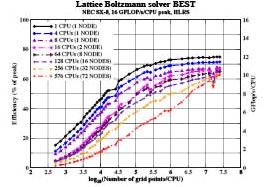
Рисунок 3 – Производительность, GFlop/s, MLup/s решателя решеточного метода Больцмана BEST в зависимости от размера области решетки, решаемой одним процессором, и количества процессоров вплоть 72 узлов 576 CPU NEC SX-8

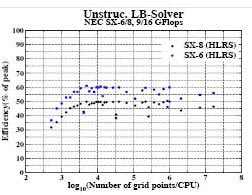
Рисунок 4 – Производительность решения неструктурированного центра решеточного метода Больцмана на NEC SX-8 в сравнении с SX-6.

Наконец мы хотели бы сосредоточиться на работе косвенной адресации массива на SX-8. В BEST вычисления осуществляются на блочно структурированной регулярной сетке. Однако для очень сложных конфигураций конечно более приемлемо хранение только тех ячеек, которые находятся внутри области потока. Для этого необходим индекс для выбора подвижных ячеек, а также должна быть сохранена информация о смежных узлах в списках индексов.
На рис.4 изображена эффективность имплементации решеточного метода Больцмана на SX-6 и на SX-8. Программа, используемая для экспериментов – совместная разработка RRZE, Institut fur Computeranwendungen im Bauingenieurwesen (CAB), Universitat Braunschweig, Section Computational Science, University of Amsterdam, Department of Medical Physics and Clinical Engineering, University of Sheffield, NEC CCRL и HLRS. Данные эксперименты идентичны предыдущим.
До настоящего времени доступна только последовательная версия программы. Это объясняет немного улучшенную производительность вычислений на маленьких сетках. В результатах, указанных ранее, коммуникация доминирует при вычислениях на маленьких сетках . Эффективность одного CPU SX-6 - на уровне 60 %. С другой стороны эффективность SX-8 - все еще 50 %, но на 10 % ниже чем на SX-6. Причина - более высокое время ожидания памяти в последней системе. Поэтому более важно на SX-8 подготовить вектор сбора/рассеивания для загрузки/хранения косвенной адресации и скрыть время ожидания выполнением других команд. Это может быть осуществлено разверткой простых циклов. Существующий цикл достаточно сложен для того, чтобы частично скрыть эти ожидание.

Перспективы

Мы также с нетерпением ждем работы новойHLRB II SGI Altix 4700. На этой системе снижение производительности вычислений между одним и двумя CPU не должно произойти из-за улучшения связи памяти. Также было бы интересно получить результаты для IBM Blue Gene в Юлихе, хотя эта архитектура не нацелена на моделирование потока.

Ссылки

[1] Lammers, P.
Direkte numerische Simulationen wandgebundener Strömungen kleiner Reynoldszahlen mit dem lattice Boltzmann Verfahren. Dissertation, Universität Erlangen-Nürnberg (2005)

[2] Qian, Y.H., d’Humières, D., Lallemand, P.
Lattice BGK models for Navier-Stokes equation Europhysical Letter 17 (1992), 479-484

[3] Wellein, G., Zeiser, T., Hager, G., Donath, S. On the single processor performance of simple lattice Boltzmann kernels. Computers Fluids (2005) in Press, corrected Proof, available online December 20, 2005

[4] Pichlmeier, J.
IBM, private communication (2005)

• Peter Lammers
• Uwe Küster

Höchstleistungsrechenzentrum Stuttgart, Germany.