| Биография |
| Автореферат |
| Поиск |
| Ссылки |
| Библиотека |
| Инд. задание |

Мищенко А.В., Попов А.А.
Источник: http://www.cfin.ru/press/management/2002-2/11.shtml
Опубликовано в номере: Менеджмент в России и за рубежом №2 / 2002
Некоторые подходы к оптимизации инвестиционного портфеля
В сложившейся мировой практике фондового рынка под инвестиционным портфелем понимается некая совокупность ценных бумаг, принадлежащих физическому или юридическому лицу, выступающая как целостный объект управления. Это означает, что при формировании портфеля и в дальнейшем, изменяя его состав и структуру, менеджер формирует новое инвестиционное качество. Основную проблему, которую необходимо решать при формировании портфеля ценных бумаг, составляет задача распределения инвестором определенной суммы денег по различным альтернативным вложениям (например, акциям, облигациям, наличным деньгам и др.) так, чтобы наилучшим образом достичь своих целей.
В первую очередь инвестор стремится к получению максимального дохода за счет: выигрыша от благоприятного изменения курса акций; дивидендов; получения твердых процентов и т.д. С другой стороны, любое вложение капитала связано не только с ожиданием получения дохода, но и с постоянной опасностью проигрыша, а, значит, в оптимизационных задачах по выбору портфеля ценных бумаг необходимо учитывать риск. В принципе для создания портфеля ценных бумаг достаточно инвестировать деньги в какой-либо один вид финансовых активов. Но современная экономическая практика показывает, что такой однородный по содержанию портфель (или недиверсифицированный) встречается очень редко. Гораздо более распространенной формой является так называемый диверсифицированный портфель, т.е. портфель с самыми разнообразными ценными бумагами. Использование диверсифицированного портфеля устраняет разброс в нормах доходности различных финансовых активов. Иными словами, портфель, состоящий из акций разноплановых компаний, обеспечивает стабильность получения положительного результата.
Смысл портфеля — улучшить условия инвестиро вания, придав совокупности ценных бумаг такие инвестиционные характеристики, которые недостижимы с позиции отдельно взятой ценной бумаги и возможны только при их комбинации.
Доходы по портфельным инвестициям представля ют собой валовую прибыль по всей совокупности бумаг, включенных в тот или иной портфель с учетом риска. Возникает проблема количественного соответствия между прибылью и риском, которая должна решаться оперативно в целях постоянного совершенствования структуры уже сформированных портфелей и формирования новых в соответствии с пожеланиями инвесторов. Надо сказать, что указанная проблема относится к числу тех, для выяснения которых достаточно быстро удается найти общую схему решения, но которые практически неразрешимы до конца.
С учетом инвестиционных качеств ценных бумаг можно сформировать различные портфели ценных бумаг, в каждом из которых будет собственный баланс между существующим риском, приемлемым для владельца портфеля, и ожидаемой им отдачей (доходом) в определенный период времени. Соотношение этих факторов и позволяет определить тип портфеля ценных бумаг.
Итак, тип портфеля — это его инвестиционная характеристика, основанная на соотношении дохода и риска. При этом важным признаком при классификации типа портфеля становится то, каким способом, при помощи какого источника данный доход получен: за счет роста курсовой стоимости или текущих выплат дивидендов, процентов.
Следует отметить, что одно из «золотых» правил работы с ценными бумагами гласит: «нельзя вкладывать все средства в ценные бумаги — необходимо иметь резерв свободной денежной наличности для решения инвестиционных задач, возникающих неожиданно» .
Данные экономического анализа подтверждают, что при определенных допущениях как желаемый размер денежных средств, предназначаемый на непредвиденные цели, так и предполагаемый размер денежных средств на трансакционные нужды зависят от процентной ставки. Поэтому инвестор, вкладывая часть средств в денежную форму, обеспечивает требуемую устойчивость портфеля. Денежная наличность может быть конвертируема в иностранную валюту, если курс национальной валюты ниже, чем иностранной. Таким образом, помимо сохранения средств достигается увеличение вложенного капитала за счет курсовой разницы.
Выше были рассмотрены принципы формирования портфеля в качественном отношении. Не менее важен количественный аспект проблемы. Сколько ценных бумаг должно быть в портфеле?
Теория инвестиционного анализа утверждает, что простая диверсификация, т.е. распределение средств портфеля по принципу «не клади все яйца в одну корзину», ничуть не хуже, чем диверсификация по отраслям, предприятиям и т.д. Кроме того, увеличение различных активов, т.е. видов ценных бумаг, находящихся в портфеле, более чем до 15 видов не дает значительного уменьшения портфельного риска. Максимальное сокращение риска достижимо, если в портфеле отобрано от 10 до 15 различных ценных бумаг; дальнейшее увеличение состава портфеля нецелесообразно, так как возникает эффект излишней диверсификации, который необходимо избегать.
Излишняя диверсификация может привести к таким отрицательным результатам, как:
-
невозможность качественного портфельного управления;
-
покупка недостаточно надежных, доходных, ликвидных ценных бумаг;
-
рост издержек, связанных с поиском ценных бумаг (расходы на предварительный анализ и т.д.);
-
высокие издержки при покупке небольших партий ценных бумаг и т.д.
Издержки по управлению излишне диверсифицированным портфелем не дадут желаемого результата, так как доходность портфеля вряд ли будет возрастать более высокими темпами, чем издержки в связи с излишней диверсификацией.
Следует отметить, что формирование и управление портфелем — область деятельности профессионалов, а создаваемый портфель — это товар, который может продаваться либо частями (продают доли в портфеле для каждого инвестора), либо целиком (когда менеджер берет на себя труд управлять портфелем ценных бумаг клиента). Как и любой товар, портфель определенных инвестиционных свойств может пользоваться спросом на фондовом рынке.
Разновидностей портфелей много, и каждый конкретный держатель придерживается собственной стратегии инвестирования, учитывая состояние рынка ценных бумаг и основательно «перетряхивая» портфель, согласно другому «золотому» правилу работы с ценными бумагами, не реже одного раза в три-пять лет. Поэтому не ставится цель охватить все многообразие существующих портфелей, а лишь определяются принципы их формирования.
Одним из действенных методов оценки при составлении инвестиционного портфеля служит моделирование. Моделирование позволяет в короткие сроки получить требуемые инвестиционные характеристики будущего портфеля в зависимости от складывающейся конъюнктуры рынка. Рассмотрим следующую оптимизационную модель.
Пусть хозяйственный субъект обладает финансовыми средствами в объеме F на интервале [0,T ]. Известно, что эти финансовые средства он может использовать для приобретения n видов ценных бумаг в объемах V1, ..., Vn. Исходная стоимость одной единицы ценных бумаг вида i составляет li, а прогнозируемая стоимость бумаг вида i к моменту времени T составляет βi. При этом будем полагать, что βi > li (i = 1...n). Необходимо выбрать такие виды ценных бумаг, чтобы максимизировать прибыль, полученную после продажи всех видов приобретенных ценных бумаг в момент времени T. Проблема формирования портфеля ценных бумаг может быть сформирована как следующая задача целочисленного линейного программирования с булевыми переменными:
![]() ,
,
![]() ,
,
![]()
Здесь в качестве целевой функции выбрано выражение, состоящее из 2-х слагаемых, первое из которых — это выручка от продажи ценных бумаг по цене βi , а второе— остаток денежных средств после формирования портфеля ценных бумаг. Учитывая, что постоянная F не оказывает влияния на оптимальное решение, получим следующую оптимизационную задачу:
![]() .
.
Согласно [10], эта задача является задачей о рюкзаке с одномерными ограничениями и принадлежит к числу так называемых NP-трудных задач, характеризующихся экспоненциальным ростом объема вычислений с ростом размерности задачи.
Для решения приведенной задачи может быть использована следующая схема метода ветвей и границ.
Шаг 1. Вычисление верхней оценки.
Вычисление верхней оценки оптимального значения целевой функции происходит
следующим образом. Все пакеты акций упорядочиваются по величине отношения ![]() (i = 1...n). Пронумеруем все пакеты соответствующим образом и
получим
(i = 1...n). Пронумеруем все пакеты соответствующим образом и
получим ![]() .
Далее, в первую очередь, финансовые ресурсы выделяются для ценных бумаг первого
вида, затем второго и т.д. до того момента, пока остатка денежных средств станет
недостаточно для приобретения полностью пакета акций вида l в объеме Vl.
В этой ситуации снимаются ограничения на приобретение всех акций пакета вида
l и приобретаются акции вида l в максимально возможном объеме. Это количество
.
Далее, в первую очередь, финансовые ресурсы выделяются для ценных бумаг первого
вида, затем второго и т.д. до того момента, пока остатка денежных средств станет
недостаточно для приобретения полностью пакета акций вида l в объеме Vl.
В этой ситуации снимаются ограничения на приобретение всех акций пакета вида
l и приобретаются акции вида l в максимально возможном объеме. Это количество
![]() вычисляется из формулы
вычисляется из формулы ![]() ,
где
,
где ![]() — остаток финансовых средств после приобретения первых l - 1 пакетов
акций (
— остаток финансовых средств после приобретения первых l - 1 пакетов
акций (![]() ).
Далее верхняя оценка прибыли вычисляется по формуле:
).
Далее верхняя оценка прибыли вычисляется по формуле:
![]() .
.
Шаг 2. Вычисление нижней оценки.
Вычисление нижней оценки целевой функции осуществляется по формуле:
![]() .
.
После того, как вычислены верхняя и нижняя оценки прибыльности для оптимального решения, исследуются все варианты формирования портфеля ценных бумаг, вычисляя при этом текущие верхние оценки для решения.
Шаг 3. Вычисление текущих верхних оценок ![]() .
.
Вычисление текущей верхней оценки при анализе очередного варианта портфеля
ценных бумаг производится каждый раз после выделения финансовых средств на приобретение
очередного пакета. Эта оценка складывается из прибыли, полученной от приобретения
ценных бумаг, на которые уже выделены деньги, и прибыли оставшихся ценных бумаг,
вычисляемой по правилу получения ![]() .
При этом, если окажется, что
.
При этом, если окажется, что ![]() ,
то данный вариант формирования портфеля не рассматривается; в противном случае
в портфель включается очередной пакет акций, и снова вычисляется
,
то данный вариант формирования портфеля не рассматривается; в противном случае
в портфель включается очередной пакет акций, и снова вычисляется ![]() .
В итоге, либо анализируемый вариант портфеля будет отвергнут, либо в результате
будет сформирован пакет, прибыль которого больше нижней оценки
.
В итоге, либо анализируемый вариант портфеля будет отвергнут, либо в результате
будет сформирован пакет, прибыль которого больше нижней оценки ![]() .
В этом случае в качестве нижней оценки принимаем полученное значение прибыли
от последнего портфеля ценных бумаг и переходим к анализу нового варианта формирования
портфеля. Работа алгоритма заканчивается либо после перебора всех вариантов
формирования портфеля, и тогда оптимальным будет тот вариант, которому соответствует
последнее значение
.
В этом случае в качестве нижней оценки принимаем полученное значение прибыли
от последнего портфеля ценных бумаг и переходим к анализу нового варианта формирования
портфеля. Работа алгоритма заканчивается либо после перебора всех вариантов
формирования портфеля, и тогда оптимальным будет тот вариант, которому соответствует
последнее значение ![]() ,
либо в случае, когда получен вариант портфеля, прибыль по которому равна
,
либо в случае, когда получен вариант портфеля, прибыль по которому равна ![]() .
.
Одной из проблем, возникающих при практическом использовании решения предложенной задачи, является достоверность прогноза стоимости ценных бумаг βi (i= 1...n). Если известна функция распределения случайных величин, задающих возможную прибыль по каждому виду ценных бумаг, то выбирается портфель, максимизирующий математическое ожидание выигрыша, либо минимизирующий риск финансовых потерь ( среднее квадратичное отклонение ). Схема решения и результаты для данной задачи подробно описаны в работе [6].
Другим подходом использования решения задачи в условиях неточного прогноза является анализ чувствительности решения к изменению величин βi. При этом возможны три варианта.
В первом случае считается, что известны минимальные значения , и необходимо
вычислить, насколько могут быть увеличены значения βi,
чтобы оптимальное решение задачи сохранилось, т. е. необходимо определить такое
![]() ,
чтобы при увеличении всех βi на любое
,
чтобы при увеличении всех βi на любое ![]() решение задачи сохранилось.
решение задачи сохранилось.
Во втором случае предполагается, что βi меняются по
правилу βi + . ![]()
В третьем случае полагаем, что βi может принимать все
значения из интервала [![]() ,
,
![]() ].
].
Рассмотрим первый случай. Пусть множество ![]() — множество всех возможных решений задачи, и пусть эти решения упорядочены по
значению величин
— множество всех возможных решений задачи, и пусть эти решения упорядочены по
значению величин ![]()
![]() .
Пусть вектор
.
Пусть вектор![]() является оптимальным. Тогда при увеличении βi наεдля
всех i = 1...n в качестве новых решений задачи могут быть только
решения
является оптимальным. Тогда при увеличении βi наεдля
всех i = 1...n в качестве новых решений задачи могут быть только
решения ![]() . Чтобы определить границу измененияεдля решения
. Чтобы определить границу измененияεдля решения ![]() ,
необходимо выяснить
,
необходимо выяснить ![]() из следующего соотношения:
из следующего соотношения:
![]() .
.
Раскроем скобки в правой части этого выражения и выразимεчерез параметры
![]() :
:
![]() .
.
Отсюда
 .
.
Пусть этот минимум достигается на каком-либо ![]() .
Тогда процедура приращения
.
Тогда процедура приращения ![]() для решения
для решения ![]() повторяется. Это происходит до тех пор, пока через конечное число шагов не произойдет
переход на решение
повторяется. Это происходит до тех пор, пока через конечное число шагов не произойдет
переход на решение ![]() ,
и тогда дальнейшее увеличение всех значений βi не приведет
к новому решению. Таким образом доказано следующее свойство оптимальных решений
задачи:
,
и тогда дальнейшее увеличение всех значений βi не приведет
к новому решению. Таким образом доказано следующее свойство оптимальных решений
задачи:
Пусть ![]() — все допустимые решения задачи, упорядоченные по возрастанию величины
— все допустимые решения задачи, упорядоченные по возрастанию величины ![]()
![]() ,
и
,
и ![]() является оптимальным решением, тогда существует такое разбиение полубесконечного
интервала
является оптимальным решением, тогда существует такое разбиение полубесконечного
интервала ![]() на конечное число отрезков, что при увеличении на
ε внутри каждого отрезка всех значений βi
оптимальное решение сохраняется. В частности, если первоначальным решением задачи
было решение xn, то при равномерном увеличении всех βi
на любое ε
на конечное число отрезков, что при увеличении на
ε внутри каждого отрезка всех значений βi
оптимальное решение сохраняется. В частности, если первоначальным решением задачи
было решение xn, то при равномерном увеличении всех βi
на любое ε
![]()
![]() решение задачи не меняется.
решение задачи не меняется.
Во втором случае, то есть когда βi меняется по правилу
βi
+ ![]() ,
схема рассуждений сохраняется, только упорядочение решений происходит по величине
,
схема рассуждений сохраняется, только упорядочение решений происходит по величине
![]()
![]() .
.
Соответственно, формула для вычисления максимального ε, при котором сохраняется
оптимальное решение ![]() ,
выглядит следующим образом:
,
выглядит следующим образом:
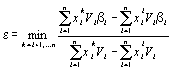 .
.
В ситуации, когда известен диапазон изменения ![]() ,
аналогично может быть предложена процедура разбиения множества, на котором меняются
значения
,
аналогично может быть предложена процедура разбиения множества, на котором меняются
значения ![]()
![]() ,
на множества
,
на множества ![]() .
При этом при изменении β на любом из подмножеств
.
При этом при изменении β на любом из подмножеств ![]() оптимальным на этом подмножестве остается решение
оптимальным на этом подмножестве остается решение ![]() .
Схема такого разбиения предложена в [4].
.
Схема такого разбиения предложена в [4].
Литература
1. Агасандян Г.А. Элементы многопериодной портфельной модели. — М.: Вычислительный центр РАН, 1997.
2. Балабанов И.Т. Основы финансового менеджмента. — М.: Финансы и статистика, 1997.
3. Минаев Ю.Н. Стабильность экономико-математических моделей оптимизации. — М.: Статистика, 1980.
4. Мищенко А.В. Модели распределения ограниченных ресурсов//Рос. экон. акад. — 1992.
«Менеджмент в России и за рубежом», ¹ 2, 2002
5. Мищенко А.В., Попов А.А. Модели управления портфелем ценных бумаг//Рос. экон. акад. — 1999.
6. Мищенко А.В., Попов А.А. Двухкритериальная задача оптимизации инвестиционного портфеля в условиях ограничений на финансовые ресурсы//Менеджмент в России и за рубежом. — 2001. — ¹ 1.
7. Ромакин М.И. Математический аппарат оптимизационных задач. — М.: Статистика, 1975.
8. Рынок ценных бумаг/Под ред. акад. А.И.Басова, В.А. Галанова. — М.: Финансы и статистика, 1996.
9. Тренев Н.Н. Управление финансами. Учебное пособие. — М.: Финансы и статистика, 1999.
10. Ху Т. Целочисленное программирование и потоки в сетях. — М.: Мир, 1975.
11. Шарп У.Ф., Александер Г.Д., Бэйли Д.В. Инвестиции. — М.: Инфра-М, 1997.
Источник: http://www.cfin.ru/press/management/2002-2/11.shtml