|

Соколов В.И.
Тема: «Исследование влияния качества приёма радиосигналов на точность
дифференциальных GPS-измерений при коротких базах»
Научный руководитель: проф., д.т.н. Гавриленко Юрий Николаевич
Цель работы: изучение влияния различных факторов на точность GPS-нивелирования при коротких базах.
Задачи:
- создание испытательного полигона;
- измерение превышений GPS-приёмником;
- обработка результатов наблюдений;
- анализ и обобщение результатов исследования.
Объект исследования: превышения, полученные в результате GPS-нивелирования.
В настоящее время назрела необходимость в обновлении пунктов высотной и плановой сети в населённых пунктах, так как большинство пунктов утрачено. Осуществить обновление геодезических сетей за сравнительно короткий срок и качественно можно с применением спутниковых технологий. Условия города таковы, что большинство геодезических наблюдений на земной поверхности производятся на незначительных расстояниях.
Кроме того, в условиях Донбасса есть необходимость в мониторинговых исследованиях подрабатываемых шахтами территорий. Достаточно часто измерения по определению превышений между точками земной поверхности при мониторинге выполняются на сравнительно небольших расстояниях (до одного километра). Измерить превышения в данном случае можно не только при помощи классического геометрического нивелирования, но и при помощи более производительных спутниковых технологий. Именно поэтому важно исследовать GPS-наблюдения в городских условиях при коротких базах.
Одним из основных условий получения хороших точностных результатов при выполнении спутниковых измерений является свободное прохождение радиосигналов от спутников к приёмнику. Но в городских условиях данное требование очень часто невыполнимо. Это вызвано, прежде всего, наличием разного рода препятствий на пути прохождения радиосигнала: зданий, сооружений, деревьев, линий электропередачи и т.д.
На рисунке 1 представлен пример, который может иметь место на практике. В данном случае сигналы, проходя от спутников к приёмнику, или не доходят до антенны приёмника, или доходят, но с прерываниями и переотражением от зданий, деревьев.

Анимация 1 - Пример некачественного приёма сигналов от спутников в условиях городской территории (Размер 14.6 КБ, 7 кадров, количесво повторений - 10, частота повторений 0.5 с)
Сигнал, исходящий от спутников, встречает следующие препятствия:
- Для спутника №1 – сигнал прерывается из-за наличия деревьев и лиственного покрова на них. Даже в период времени, когда деревья не имеют лиственного покрова, наличие стволов деревьев и крупных веток прерывает сигнал на непродолжительный интервал времени.
- Для спутника №2 – сигнал экранирует от рядом припаркованного крупного автомобиля.
- Для спутника №3 – происходит переотражение сигнала от близлежащего дома, вследствие чего увеличивается значение измеряемой псевдодальности, что вносит свою немалую ошибку.
Данный эффект называется многопутностью распространения сигнала. Он появляется в результате вторичных отражений сигнала спутника от крупных препятствий, расположенных в непосредственной близости от приемника. При этом возникает явление интерференции, и измеренное расстояние оказывается больше действительного. Аналитически данную погрешность оценить достаточно трудно, а наилучшим способом борьбы с нею считается рациональное размещение антенны приемника относительно препятствий. [2]
- Для спутника №4 – на точность наблюдений оказывают влияние ионосфера и тропосфера. Данные факторы оказывают влияние на распространение сигналов от всех спутников.
Ионосфера – это ионизированный атмосферный слой в диапазоне высот 50 – 500 км, который содержит свободные электроны. Наличие этих электронов вызывает задержку распространения сигнала спутника, которая прямо пропорциональна концентрации электронов и обратно пропорциональна квадрату частоты радиосигнала. Для компенсации возникающей при этом ошибки определения псевдодальности используется метод двухчастотных измерений на частотах L1 и L2 (в двухчастотных приемниках).
Тропосфера – самый нижний слой атмосферы (до высоты 8 – 13 км). Она также обуславливает задержку распространения радиосигнала от спутника. Величина задержки зависит от метеопараметров (давления, температуры, влажности), а также от высоты спутника над горизонтом. Компенсация тропосферных задержек производится путем расчета математической модели этого слоя атмосферы. Необходимые для этого коэффициенты содержатся в навигационном сообщении. [2]
- Для спутника №5 – сигнал проходит непосредственно через источник сильного электромагнитного излучения (линия электропередачи).
- Для спутника №6 – имеет место абсолютное непрохождение сигнала, вызванное наличием крупного препятствия в виде девятиэтажного здания.
Указанные на рисунке причины ухудшения точности измерений комплектом GPS-приёмников (кроме влияния ионосферы и тропосферы) может устранить или хотя бы уменьшить их влияние сам наблюдатель благодаря грамотному планированию измерений. Грамотное планирование заключается в выборе наиболее выгодного места расположения приёмника и выборе лучшего времени для наблюдений (такого при котором можно обеспечить наблюдение достаточного количества спутников с хорошей геометрией их расположения (GDOP)).
При планировании высокоточных измерений обязательным является составление абриса препятствий на точке предполагаемых наблюдений. На рисунке 2а представлен пример абриса препятствий без учёта деревьев для одного из пунктов испытательного полигона, на рисунке 2б – с учётом деревьев для того же пункта. По внешнему виду данных абрисов можно сделать вывод о том, что в летний период времени наличие лиственного покрова может привести к существенному ухудшению точности GPS-наблюдений.

Рисунок 2 - Абрисы препятствий на пункте
На рисунке 3 представлен результат удачного планирования измерений, при котором минимизировано влияние тех факторов, которые имели место на рисунке 1.

Анимация 3 - Пример качественного приёма сигналов от спутников в условиях городской территории (Размер 27.8 КБ, 8 кадров, количесво повторений - 10, частота повторений 0.5 с)
В данном примере представлены не все факторы, которые могут оказывать влияние на точность GPS-наблюдений, а лишь те, на которые может повлиять наблюдатель.
Для исследования влияния качества приёма радиосигналов на точность дифференциальных GPS-измерений при коротких базах в центре города Донецка был заложен испытательный полигон (см. рис. 4), состоящий из шести точек (Драм, Совет, Стратонавт, Фонтан, Шевченко, Юз). Общая протяжённость полигона с юга на север – 2 км, превышение – 45 м. На данном полигоне было выполнено измерение 11 векторов в статическом режиме двухчастотным GPS-приёмником Z-Max. Продолжительность сессии наблюдений 30 мин., частота записи данных 1 с, угол маски 10 градусов. Параллельно бригадой студентов группы ИГ-03 выполнено высокоточное нивелирование по программе второго класса.

Рисунок 4 - Схема испытательного полигона
Обработка результатов GPS-наблюдений выполнялась с применением программы GNSS Studio.
Для каждого из векторов были получены отклонения результатов GPS-наблюдений от результатов нивелирования второго класса. Отклонения получены для разных отсчётных поверхностей, таких как: земной эллипсоид, эллипсоид Красовского, модель геоида EGM-96 (см. табл. 1). В данной таблице вектора расположены в порядке возрастания длин.
Таблица 1 – Отклонение результатов GPS-нивелирования от результатов нивелирования второго класса
| Название вектора |
Длина вектора, м |
Земной эллипсоид. Отклонение, мм |
Эллипсоид Красовского. Отклонение, мм |
Модель геоида EGM-96. Отклонение, мм |
| Шевченко-Совет |
271.180 |
-5 |
0 |
1 |
| Стратонавт-Фонтан |
339.553 |
-7 |
-6 |
-2 |
| Фонтан-Драм |
389.897 |
-46 |
-42 |
-38 |
| Совет-Юз |
<452.638 |
-23 |
-21 |
-15 |
| Шевченко-Юз |
558.736 |
-10 |
-13 |
-6 |
| Стратонавт-Драм |
717.133 |
-25 |
-19 |
-12 |
| Драм-Шевченко |
791.776 |
-3 |
-3 |
6 |
| Фонтан-Шевченко |
1143.308 |
-33 |
-30 |
-16 |
| Фонтан-Совет |
1228.301 |
-39 |
-41 |
-26 |
| Стратонавт-Совет |
1561.449 |
-42 |
-42 |
-24 |
| Фонтан-Юз |
1667.321 |
-32 |
-32 |
-11 |
Наиболее подходящей для данного участка работ является модель геоида EGM-96, так как значения превышений, обработанных относительно EGM-96, наиболее близки к результатам нивелирования второго класса.
Если внимательно посмотреть на отклонения, то можно заметить, что отклонения для каждой из систем содержат в себе систематическую составляющую (имеют один и тот же знак).
Наиболее вероятной причиной наличия систематической составляющей в отклонениях является наличие уклонения отвесной линии (см. рис. 5).

Рисунок 5 - Уклонение овесной линии
Уклонение отвесной линии по некоторому направлению с геодезическим азимутом А [1] будет равно:

где  – проекция полного уклонения отвесной линии на меридиан; – проекция полного уклонения отвесной линии на меридиан;
 – проекция полного уклонения отвесной линии на первый вертикал. – проекция полного уклонения отвесной линии на первый вертикал.
По каждому из одиннадцати измеряемых векторов можно составить уравнения, которые дадут систему параметрических уравнений.
Параметрическое уравнение будет иметь вид:

где h – превышение между точками, измеренное комплектом спутниковых приёмников;
S – расстояние между точками, измеренное комплектом спутниковых приёмников;
H – превышение между точками, полученное по результатам нивелирования второго класса;
V – поправка в превышение.
С учётом формулы (1) система будет иметь вид:

Решение параметрических уравнений выполнялось для трёх вышеуказанных отсчётных систем. В результате для каждого из уравнений были определены свои составляющие уклонения отвесных линий ( , , ) (см. табл.2). ) (см. табл.2).
Таблица 2 – Определение составляющих уклонения отвесной линии
| Отсчётная поверхность |
Составляющие уклонения отвесной линии |
Оценка точности определения составляющих уклонения отвесной линии |
 , ,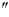 |
 , ,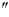 |
M , ,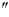 |
M , ,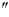 |
| Земной эллипсоид |
4.8 |
11.5 |
0.9 |
5.5 |
| Эллипсоид Красовского |
4.9 |
7.2 |
0.9 |
5.5 |
| Модель геоида EGM-96 |
2.4 |
7.3 |
0.9 |
5.4 |
Из оценки точности видно, что величина  определена достаточно надёжно, а вот величина определена достаточно надёжно, а вот величина  определена плохо. Причиной этого является вытянутость полигона в меридиональном направлении, т.е. проекция уклонения на меридиан определяется гораздо более точно, чем проекция на первый вертикал. Именно поэтому необходимо далее развивать полигон в направлении, перпендикулярном меридиану. определена плохо. Причиной этого является вытянутость полигона в меридиональном направлении, т.е. проекция уклонения на меридиан определяется гораздо более точно, чем проекция на первый вертикал. Именно поэтому необходимо далее развивать полигон в направлении, перпендикулярном меридиану.
К чему же может привести значение величины составляющей уклонения отвесной линии, равное 2,4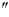 для вектора длиной 2000 м? Это даст систематическую ошибку 23 мм (sin2.4 для вектора длиной 2000 м? Это даст систематическую ошибку 23 мм (sin2.4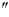 *2000 м). Для таких высокоточных измерений, какими являются спутниковые наблюдения, 23 мм – это очень много. *2000 м). Для таких высокоточных измерений, какими являются спутниковые наблюдения, 23 мм – это очень много.
Перед вами уже знакомая таблица, но с добавлением последней колонки с поправками, полученными в результате решения параметрических уравнений (см. табл. 3).
Таблица 3 – Сводная таблица
| Название вектора |
Длина вектора, м |
Земной эллипсоид. Отклонение,мм |
Эллипсоид Красовского. Отклонение, мм |
Модель геоида EGM-96. Отклонение, мм |
Поправка, мм |
| Шевченко-Совет |
271.180 |
-5 |
0 |
1 |
-4 |
| Стратонавт-Фонтан |
339.553 |
-7 |
-6 |
-2 |
-13 |
| Фонтан-Драм |
389.897 |
-46 |
-42 |
-38 |
11 |
| Совет-Юз |
<452.638 |
-23 |
-21 |
-15 |
4 |
| Шевченко-Юз |
558.736 |
-10 |
-13 |
-6 |
-27 |
| Стратонавт-Драм |
717.133 |
-25 |
-19 |
-12 |
5 |
| Драм-Шевченко |
791.776 |
-3 |
-3 |
6 |
5 |
| Фонтан-Шевченко |
1143.308 |
-33 |
-30 |
-16 |
-15 |
| Фонтан-Совет |
1228.301 |
-39 |
-41 |
-26 |
7 |
| Стратонавт-Совет |
1561.449 |
-42 |
-42 |
-24 |
-5 |
| Фонтан-Юз |
1667.321 |
-32 |
-32 |
-11 |
-6 |
В таблице 4 представлены значения средних квадратических ошибок для трёх отсчётных поверхностей (Земной эллипсоид, эллипсоид Красовского, геоид EGM-96) до и после учёта величины уклонения отвесной линии в превышениях, измеренных комплектом GPS-приёмников. В первом случае было бы не правильно, если бы мы рассчитали СКО (так как имела место значительная систематическая ошибка), а теперь посмотрите, как изменилась ситуация после учёта величины уклонения отвесной линии.
Таблица 4 – Влияние учёта уклонения отвесной линии на точность измерения превышений комплектом GPS-приёмников
| Показатель |
Земной эллипсоид |
Эллипсоид Красовского |
Модель геоида EGM-96 |
| Средняя квадратическая ошибка по Гауссу до учета уклонения, мм |
28 |
27 |
18 |
| Средняя квадратическая ошибка по Гауссу после учета уклонения, мм |
11 |
11 |
11 |
| Уменьшение средней квадратической ошибки |
2.5 |
2.5 |
1.6 |
ВЫВОДЫ
1. За счёт учёта систематической ошибки может быть существенно повышена точность GPS-нивелирования.
2. Необходимо изменить схему исследуемого полигона для более точного определения проекции полного уклонения отвесной линии на первый вертикал.
ПЕРЕЧЕНЬ ССЫЛОК
1. «Высшая геодезия». Зданович В.Г., Беликов А.Н., Гусев Н.А., Звонарёв К.А. М., изд-во "Недра", 1970, стр. 512.
2. http://www.geomatica.kiev.ua/training/DataCapture/GPS/chapter100.html
|








 определена достаточно надёжно, а вот величина
определена достаточно надёжно, а вот величина  определена плохо. Причиной этого является вытянутость полигона в меридиональном направлении, т.е. проекция уклонения на меридиан определяется гораздо более точно, чем проекция на первый вертикал. Именно поэтому необходимо далее развивать полигон в направлении, перпендикулярном меридиану.
определена плохо. Причиной этого является вытянутость полигона в меридиональном направлении, т.е. проекция уклонения на меридиан определяется гораздо более точно, чем проекция на первый вертикал. Именно поэтому необходимо далее развивать полигон в направлении, перпендикулярном меридиану.
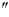 для вектора длиной 2000 м? Это даст систематическую ошибку 23 мм (sin2.4
для вектора длиной 2000 м? Это даст систематическую ошибку 23 мм (sin2.4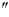 *2000 м). Для таких высокоточных измерений, какими являются спутниковые наблюдения, 23 мм – это очень много.
*2000 м). Для таких высокоточных измерений, какими являются спутниковые наблюдения, 23 мм – это очень много.
