|

Vladislav I. Sokolov
Subject: «Studying of the influence of radio-signal reception quality on accuracy
of differential GPS measurements with short bases»
Thesis Supervisor: Professor and Ph.D. in Technical Science Yuriy N. Gavrilenko
Goal: studying of the influence of different factors on accuracy of GPS leveling with short base.
Objectives:
- creating a testing site;
- measuring elevations with a GPS receiver;
- processing observation results;
- analyzing and summarizing research results.
Research object: elevations received as the result of GPS leveling.
At present time we have reached the point when it is really necessary to renew altimetric and planimetric networks at urban areas as most network spots have been lost. Quick and high quality renewal of geodetic networks can be carried out by using satellite technologies. The city conditions suggest that most geodetic observations on the earth surface should be carried out for short distances.
In addition, in the Donbass Area we have the necessity for monitor research of coal mine areas. Quite often at monitoring, measurements of elevations between the spots of the earth surface are made for short distances. (up to 1 kilometer). In this case it is possible to take measurements not just using classical geometric leveling but also more efficient satellite technologies. That’s why it is so important to study GPS observations in urban conditions with a short base.
One of the key aspects for getting good accurate results when making satellite measurements is free transmission of radio signals from satellite to receiver. However in urban areas it’s quite hard to meet the requirement. First of all this is connected with the fact that there are lots of obstacles on the way of the signal (buildings, constructions, power transmission lines, etc.).
In picture 1 there is an example, which we can face in practice. In this case the signals when being transmitted from satellites to receivers either fail to get to the receiver antenna or get to the receiver however they are either broken or reflected from buildings and trees.

Picture 1 - Example of poor reception of signals from satellites in urban area (Size 14.6 KB, 7 slides, number of repeats - 10, frequency of repeats 0.5 ñ)
The signal transmitted from satellites comes up against the following obstacles:
- For satellite N1 – the signal gets broken because of trees and foliage. Even in case of naked trees the signal gets broken for some time because of tree trunks and large twigs.
- For satellite N2 – the signal is screened from the large vehicle parked nearly.
- For satellite N3 – the signal is reflected from the neighboring house resulting in the increase in the value of the measured pseudorange and causing quite a big mistake.
This effect is called a multiple signal spreading. It appears as the result of signal secondary reflections from large obstacles located in immediate proximity to the receiver. This is also accompanied by interference phenomenon and the measured distance appears to be bigger than the actual value. Analytically it is quire hard to measure the error and the best method to fight it is to put the receiver antenna in the best location against the obstacles. [2]
- For satellite N4 – the accuracy of observations are influenced by ionosphere and troposphere. These factors influence the signal transmissions of all satellites.
Ionosphere is an ionized part of atmosphere at the altitude ranging between 50 -500 km. It contains free electrons, which cause delays in satellite signal transmission; the delays being in pro rata proportion to the concentration of electrons and in inverse proportion to the squared radio signal frequency. In order to compensate the error of pseudorange we use the method of a two frequency measurement on Frequencies L1 and L2 (two frequency receivers).
Troposphere is the lowest portion of Earth’s atmosphere (up to 8-13 km altitude). It also accounts for the delays in radio signal transmission from satellites. The time of delay depends on meteorological parameters (pressure, temperature, humidity) as well as on the satellite height above the horizon. Troposphere delay compensation is made through calculation of a mathematical model of this layer of atmosphere. The required coefficients are given in the navigation message. [2]
- For satellite N5 – the signal goes directly through a source of strong electromagnetic radiation (power transmission line).
- For satellite N6 – absolute signal nonpassage caused by a large obstacle in the form of a 9-storied building.
The reasons for measurement accuracy reduction with GPS receivers as specified in the picture (with the exception of influence of ionosphere and troposphere) can be eliminated or at least mitigated by the observer himself using technically correct measurement planning. Technically correct measurement planning means choosing the best location for the receiver and the best time for observation (that is the time, which allows you to observe enough number of satellites with good delusion of precision (GDOP).
When making high accuracy measurements its’ important to compile the sketches of obstacles at the spot of supposed observations. Picture 2a gives an example of the sketch, which does not take into account trees for one of the testing sites and picture 2b – example of the sketch, which takes into account trees for the same testing site. The sketches clearly demonstrate that in summer foliage can significantly reduce the accuracy of GPS observations.

Picture 2 - The sketches of obstacles at the spot of supposed observations
Picture 3 shows successful measurement planning results as the influence of the factors as shown in picture 1 are minimized.

Picture 3 - Example of good reception of signals from satellites in urban area (Size 27.8 KB, 8 slides, number of repeats - 10, frequency of repeats 0.5 s)
The present example does not include all the factors, which can influence the accuracy of GPS observations; it just includes the factors, which can be controlled by an observer.
In order to study the influence of radio signal reception quality on the accuracy of differential GPS measurements with short bases a testing site was built in the center of the City (see picture 4) consisting of six spots (Sovet, Dram, Stratonavt, Fountan, Shevchenko, Uz). The testing site stretches from south to north for 2 km, elevation – 45 m. At the testing site we measured 11 vectors in a static mode with a two frequency Z-Max receiver (made by French Company Thales) (accuracy of the receiver). The session lasted for 30 minutes, data record frequency – 1s, mask angle – 10 degrees.

Picture 4 - Plan of testing site
The results of GPS observations were processed by using the program GNSS Studio.
For each vector we received deviations between the results of GPS observations and the results of second order leveling. The deviations were received from different datum surfaces, such as: earth ellipsoid, Krasovsky ellipsoid, EGM-96 geoid model (see table 1). In the present table the vectors are shown in length ascending order.
Table 1 – Deviation of GPS leveling results from second-order leveling results
| Name of vector |
Range of vector, ì |
Earth ellipsoid. Deviation, mm |
Krasovsky ellipsoid. Deviation, mm |
EGM-96. Deviation, mm |
| Shevchenko-Sovet |
271.180 |
-5 |
0 |
1 |
| Stratonavt-Fontan |
339.553 |
-7 |
-6 |
-2 |
| Fontan-Dram |
389.897 |
-46 |
-42 |
-38 |
| Sovet-Uz |
<452.638 |
-23 |
-21 |
-15 |
| Shevchenko-Uz |
558.736 |
-10 |
-13 |
-6 |
| Stratonavt-Dram |
717.133 |
-25 |
-19 |
-12 |
| Dram-Shevchenko |
791.776 |
-3 |
-3 |
6 |
| Fontan-Shevchenko |
1143.308 |
-33 |
-30 |
-16 |
| Fontan-Sovet |
1228.301 |
-39 |
-41 |
-26 |
| Stratonavt-Sovet |
1561.449 |
-42 |
-42 |
-24 |
| Fontan-Uz |
1667.321 |
-32 |
-32 |
-11 |
EGM-96 geoid model is the best for this type of works as the elevation values processed in regard to EGM-96 are the closest to the results of second-order leveling.
If we carefully study the deviations we can notice that deviations for each system contain a systemic component (have the same sign).
The most likely reason for a systemic component in deviations is the existence of declination of a plumb line (see picture 5).

Picture 5 - Plumb line declination
Plumb line declination to some direction of À [1] geodetic azimuth will be:

where  – projection of complete plumb line declination on a meridian; – projection of complete plumb line declination on a meridian;
 – projection of complete plumb line declination on the first vertical. – projection of complete plumb line declination on the first vertical.
For each of the eleven measurable vectors an equation may be generated, thus resulting in a system of parametric equations.
The parametric equation takes the following form:

where h – elevation between posts measured by a set of satellite borne receivers;
S – distance between posts measured by a set of satellite borne receivers;
H – elevation between posts calculated by second-order leveling;
V – allowance for elevation.
Subject to formula (1) the system takes the following form:

Solution of parametric equations was calculated for three reading systems above. As a result, components of plumb line declination ( , , ) (see table 2) were determined for each of the systems. ) (see table 2) were determined for each of the systems.
Table 2 – Components of plumb line declination
| Datum surface |
Components of plumb line declination |
Accuracy estimate for components of plumb line declination |
 , ,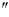 |
 , ,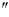 |
M , ,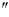 |
M , ,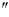 |
| Earth ellipsoid |
4.8 |
11.5 |
0.9 |
5.5 |
| Krasovsky ellipsoid |
4.9 |
7.2 |
0.9 |
5.5 |
| EGM-96 |
2.4 |
7.3 |
0.9 |
5.4 |
On the basis of the accuracy estimate it appears that  value is determined reliably enough, while value is determined reliably enough, while  value is badly determined. This results from meridional elongation of the testing site, i.e. the projection of declination on a meridian is determined more accurately that the projection of the first vertical. That is why the proving ground must be further developed in the direction perpendicular to the meridian. value is badly determined. This results from meridional elongation of the testing site, i.e. the projection of declination on a meridian is determined more accurately that the projection of the first vertical. That is why the proving ground must be further developed in the direction perpendicular to the meridian.
What may a component of the plumb line declination of 2.4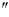 result in for a 2,000 meter vector? It will give a systematic error of 23 mm. For such high-accuracy measurements as satellite observations, 23 mm is quite a lot. result in for a 2,000 meter vector? It will give a systematic error of 23 mm. For such high-accuracy measurements as satellite observations, 23 mm is quite a lot.
Here you can see the table already known to you but containing additional column with allowances calculated through parametric equations (see table 3).
Table 3 – Consolidated table
| Name of vector |
Range of vector, m |
Earth ellipsoid. Deviation, mm |
Krasovsky ellipsoid. Deviation, mm |
EGM-96. Deviation, mm |
Allowance, mm |
| Shevchenko-Sovet |
271.180 |
-5 |
0 |
1 |
-4 |
| Stratonavt-Fontan |
339.553 |
-7 |
-6 |
-2 |
-13 |
| Fontan-Dram |
389.897 |
-46 |
-42 |
-38 |
11 |
| Sovet-Uz |
<452.638 |
-23 |
-21 |
-15 |
4 |
| Shevchenko-Uz |
558.736 |
-10 |
-13 |
-6 |
-27 |
| Stratonavt-Dram |
717.133 |
-25 |
-19 |
-12 |
5 |
| Dram-Shevchenko |
791.776 |
-3 |
-3 |
6 |
5 |
| Fontan-Shevchenko |
1143.308 |
-33 |
-30 |
-16 |
-15 |
| Fontan-Sovet |
1228.301 |
-39 |
-41 |
-26 |
7 |
| Stratonavt-Sovet |
1561.449 |
-42 |
-42 |
-24 |
-5 |
| Fontan-Uz |
1667.321 |
-32 |
-32 |
-11 |
-6 |
Table 4 contains average quadratic errors for three datum surfaces (Earth ellipsoid, Krasovsky ellipsoid, EGM-96) before and after plumb line declination in elevations measured by a set of GPS receivers is taken into consideration. In the first case it would be wrong if we calculated average quadratic errors (for we have considerable systematic error), and now have a look at the situation after plumb line declination is taken into account.
Table 4 – Impact of plumb line declination on elevation accuracy measured by a set of GPS receivers
| Index |
Earth ellipsoid |
Krasovsky ellipsoid |
EGM-96 |
| Gauss' average quadratic error before declination is taken into consideration, ìì |
28 |
27 |
18 |
| Gauss' average quadratic error after declination is taken into consideration , ìì |
11 |
11 |
11 |
| Decrease in average quadratic error |
2.5 |
2.5 |
1.6 |
CONCLUSIONS
1. Accuracy of GPS leveling may be significantly enhanced through consideration of systematic error.
2. Plan of the testing site must be changed to get more accurate projection of complete plumb line declination on the first vertical.
REFERENCES

2. http://www.geomatica.kiev.ua/training/DataCapture/GPS/chapter100.html
This work is incomplete and presents information giving no rise to doubt for the author.
|








 value is determined reliably enough, while
value is determined reliably enough, while  value is badly determined. This results from meridional elongation of the testing site, i.e. the projection of declination on a meridian is determined more accurately that the projection of the first vertical. That is why the proving ground must be further developed in the direction perpendicular to the meridian.
value is badly determined. This results from meridional elongation of the testing site, i.e. the projection of declination on a meridian is determined more accurately that the projection of the first vertical. That is why the proving ground must be further developed in the direction perpendicular to the meridian.
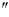 result in for a 2,000 meter vector? It will give a systematic error of 23 mm. For such high-accuracy measurements as satellite observations, 23 mm is quite a lot.
result in for a 2,000 meter vector? It will give a systematic error of 23 mm. For such high-accuracy measurements as satellite observations, 23 mm is quite a lot.

