Приложение прогнозирования ВВП

1. Линейная модель регрессии.
2. Эквивалентная нейронная сеть.
3. Создание прогнозов.
4. Относительное прогнозирующее исполнение.

Эмпирический пример – возможно, наилучший способ проиллюстрировать различия между нейронной сетью и линейной регрессионной моделью. Нейронная сеть, поэтому, и была создана, чтобы прогнозировать квартальный рост реального валового внутреннего продукта Канады. Эта модель сравнивается с линейной регрессионной моделью, развитой в Отделе Финансов Лэми (1999). Для облегчения сравнения, нейронная сеть использует точно такие же каузальные величины и такой же период выборки, как и линейная регрессионная модель. Любые различия в результатах могут, следовательно, быть приписаны исключительно процедуре оценки.

Лэми (1999) разработал точную модель для одно-квартальных будущих прогнозов роста реального валового внутреннего продукта Канады. Модель выполнена очень хорошо, как во входной, так и в выходной выборках. За период с 1978Q1 до 1998Q2, его модель объясняет 82 процента несоответствий реального роста валового внутреннего продукта. Предполагаемые коэффициенты также очень стабильны, когда модель оценена в другие периоды выборки. К тому же, модель является весьма скупой, поскольку она содержит только следующие шесть каузальных величин (с их сокращением в скобках):

• Квартальный темп прироста Канадского Финансового индекса ведущих индикаторов экономической деятельности (задержка с одним кварталом) ( L_t-1 )
• Рост Занятости (одновременный) ( E_t )
• Рост Занятости (задержка с одним кварталом) ( E_t-1 )
• Индекс Совета Конференции потребительского доверия (одновременный) ( C_t )
• Первое различие реальной долгосрочной процентной ставки (задержка в 9 кварталов) ( R_t-9 )
• Первое различие федерального государственного бюджетного баланса как части ВВП(задержка в 3 квартала) ( F_t-3 )

Четыре фиктивных переменные были добавлены, чтобы управлять для четырех кварталов, которые рассматриваются как выбросы (четыре рассматриваемые квартала - 1980Q3, 1981Q1, 1986Q4 и 1991Q3). Для достижения целей рассматриваемого поясняющего примера и для того, чтобы оставлять некоторые данные для прогнозов выходной выборки, линейная модель регрессии была оценена, используя данные с 1978Q1 по 1993Q2 (62 наблюдений). Результаты оценки даются в уравнении (1):

GDP_t = -1.695 + 0.075•L_t-1 + 0.304•E_t + 0.251•E_t-1 + 0.019•C_t - 0.175•R_t-9
- 0.320•F_t-3 - 1.155•D₁ + 1.168•D₂ - 0.906•D₃ - 0.843•D₄ + e_t (1) ,

где D₁, D₂, D₃ and D₄ - фиктивные переменные, и e_t - остаточный срок. Все коэффициенты значительно отличаются от нуля на уровне доверия 95 процентов.

В начало

Определение количества входов и выходов сети - простой процесс. Линейная модель регрессии, описанная выше, имеет шесть регрессоров и четыре фиктивных переменные. Наша нейронная сеть будет, поэтому, содержать десять входов. Так как мы имеем только одну зависимую переменную, сеть будет иметь единственный выход. Как объясняется в Разделе 2.2, количество скрытых модулей, включаемых в сеть - в основном, результат метода проб и ошибок. Для рассматриваемого поясняющего примера была выбрана архитектура только с двумя скрытыми модулями. Хотя эта архитектура, вероятно, слишком упрощена, чтобы фиксировать сложность проблемы вручную, ее простота облегчит понимание динамики модели. Назначение этого раздела, таким образом, состоит в представлении конкретного примера сети, а не в развитии высокоэффективного инструмента прогноза. Следовательно, сеть, представленную здесь нельзя рассматривать как наилучшую возможную модель, которую нейронные сети могут предложить.

Рисунок 9 иллюстрирует архитектуру сети. Это - полностью соединенная сеть, то есть все входы подключены ко всем скрытым модулям. Сроки смещения включены как для обоих скрытых модулей ( BiasН ), так и для модуля вывода ( BiasO ). Кроме того, прямые соединения были добавлены между входами и выходами (подчеркнутые штриховой линией стрелки), таким образом, приводя к увеличенной нейронной сети. Как объяснено выше, расширенная нейронная сеть вкладывается в линейную модель регрессии. Скрытые модули имеют гиперболическую функцию активации тангенса, в то время как модуль вывода имеет функцию активации идентичности.

Рано останавливающаяся процедура использовалась, чтобы оценивать 35 весов сети (литература по нейронной сети говорит о том, что перемасштабирование данных часто полезно, чтобы улучшить точность прогноза, потому что алгоритмы оценки имеют тенденцию выполняться лучше, когда входные значения являются маленькими и сосредоточенными вокруг ноля. В сети, представленной здесь, только Индекс Совета Конференции потребительского доверия был модифицирован делением всех значений на 100. Поэтому, основное значение индекса - 1 вместо 100.) Чтобы осуществлять эту процедуру, выборка была разделена на три отдельных части: обучающий набор (1978Q1 к 1993Q2), набор проверки правильности (1993Q3 к 1995Q4) и проверочный набор (1996Q1 к 1998Q2). Обучающий набор, который соответствуют периоду входной выборки линейной регрессионной модели в уравнении (1), является единственной порцией данных, которые обучающий алгоритм использовал для оценки весов сети.

Рисунок 9

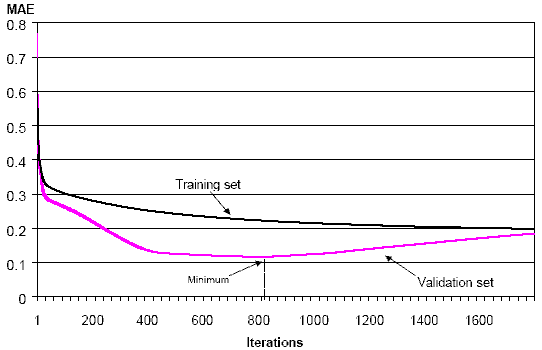
Рисунок 10 иллюстрирует развитие средней абсолютной ошибки (САО) (программное обеспечение, оценивающее веса сети (MATLAB с инструментарием Netlab), обеспечивает среднюю абсолютную ошибку прогноза, а не среднюю взвешенную ошибку, как обсуждается в Разделе 3. Это не оказывает существенного влияния на результаты. Инструментарий Netlab может быть бесплатно загружен с http://www.ncrg.aston.ac.uk/netlab/index.html.) в обучении и проверке правильности во время итерационного процесса. САО в наборе проверки правильности достигает минимума после 819 итераций, в то время как САО в обучающем наборе продолжает непрерывно уменьшаться. Чтобы уменьшить риск сверхприспособления сети, процедура, поэтому была остановлена после 819 итераций, с САО 0.118 в наборе проверки правильности.

Рисунок 10

На рисунке 11, предполагаемые веса представлены для различных разделов сети. Подключения от входов и Bias_H к скрытому модулю H₁ представлены на панели A. Панель B представляет подобную диаграмму для подключений между входами и H₂. Панель C отображает предполагаемые веса между скрытыми модулями и модулем вывода, и Панель D иллюстрирует прямые подключения от входов к выходам..

Рисунок 11

В начало

Предположим, мы хотим спрогнозировать реальный рост ВВП для 1998Q2. Значения регрессоров/входов для 1998Q2 представлены ниже:

L_t-1 = 0.66, E_t = 0.67, E_t-1 = 0.75, C_t = 1.1497, R_t-9 = 1.13, F_t-3 = 0.84,
D₁ = D₂ = D₃ = D₄ = 0.

В случае линейной модели регрессии, прогноз для 1998Q2 является прямым:

GDP_t = -1.695 + 0.075•(0.66) + 0.304•(0.67) + 0.251•(0.75) + 0.019•(1.1497) - 0.175•(1.13)
- 0.320•(0.84) - 1.155•(0) + 1.168•(0) - 0.906•(0) - 0.843•(0) = 0.46 (2)

Линейная регрессионная модель прогнозирует реальный рост валового внутреннего продукта на 0.46 процентов в 1998Q2.

В нейронной сети, первый шаг заключается в вычислении значения скрытых модулей. Для получения значения для H1, сеть должна сначала умножить значение каждого входа на соответствующий вес, как изображено в Панели А рисунка 11. Это значение обозначено Z₁.

Z₁ = -0.401 - 0.058•(0.66) + 0.292•(0.67) - 0.207•(0.75) + 0.550•(1.1497) + 0.754•(1.13)
+ 0.294•(0.84) - 1.038•(0) + 0.487•(0) - 0.290•(0) - 0.209•(0) = 1.332 (3)

Значение H₁ получено подставлением Z₁ в гиперболическую функцию активации тангенса:

H₁ = TANH(1.332) = ( e^Z1 - e^-Z1) / ( e^Z1 + e^-Z1)
= ( e^1.332 - e^-1.332) / ( e^1.332 + e^-1.332) = 0.8697 (4)

Подобным способом, используя веса в Панели B фигуры 11, H₂ можно показать выражением:

H₂ = TANH(-0.6999) = ( e^-0.6999 - e^-(-0.6999)) / ( e^-0.6999 + e^-(-0.6999)) = -0.643 (5)

Используя аналогию человеческого мозга и помня, что значения, произведенные гиперболической функцией тангенса, находятся в пределах между -1 и 1, можно было сказать, что нейрон, H₁ сильно возбуждается особыми раздражителями, обеспеченными входными значениями, в то время как H₂ возбуждается умеренно.

Модуль выхода GDP_t имеет идентичную активационную функцию, означая, что гиперболическая функция тангенса не будет использоваться, чтобы обработать линейную комбинацию "раздражителей", достигающих модуля вывода. Прогноз сети просто будет равен линейной комбинации скрытых модулей (панель C рисунка 11) и входов (панель D):

GDP_t = -0.081 + 1.45•H₁ + 0.604•H₂ + 0.084•L_t-1 + 0.335•E_t + 0.751•E_t-1 + 0.339•C_t
- 1.067•R_t-9 - 0.649•F_t-3 + 0.048•D₁ + 0.21•D₂ - 0.256•D₃ - 0.55•D₄ (6)

Вычисление этого выражения со значениями для 1998Q2 дает такой результат:

GDP_t = -0.081 + 1.45•(0.8697) + 0.604•(-0.6043) + 0.084•(0.66) + 0.335•(0.67) + 0.751•(0.75) + 0.339•(1.1497)
- 1.067•(1.13) - 0.649•(0.84) + 0.048•(0) + 0.21•(0) - 0.256•(0) - 0.55•(0) = 0.30 (7)

Сеть поэтому прогнозирует реальный рост валового внутреннего продукта на 0.30 процента для 1998Q2, который значительно менее точен, чем прогноз линейной модели. Очевидно, вычисления, требуемые для прогноза, с использованием нейронной сети значительно более сложны, чем в случае линейной модели регрессии. К счастью, эти вычисления могут быть мгновенно реализованы тем же самым программным обеспечением, которое оценивало веса сети.

Уравнение (6) ясно иллюстрирует, как расширенная нейронная сеть охватывает линейную модель регрессии. Если второй и третий сроки правой стороны этого уравнения удалены, уравнение (6) становится простой линейной комбинацией входов. Эти два срока, которые являются нелинейными преобразованиями входов, помогают сети фиксировать нелинейную взаимосвязь среди переменных. Если бы сеть не обнаружила никаких нелинейностей в данных, генерирующих процесс, то предполагаемые веса для H₁ и H₂ были бы равны нулю, и сеть стала бы стандартной линейной регрессионной моделью. В данном примере, ненулевые значения весов для H₁ и H₂ предлагают наличие некоторых нелинейностей.

В начало

Действительно ли все эти трудные вычисления стоят того? Сравнение точности прогноза обоих методов обеспечивает некоторое понимание этого вопроса. Таблица 1 сравнивает прогнозирующее исполнение этой нейронной сети и линейной регрессионной модели для одно-квартальных будущих прогнозов. Было использовано три общих критерия для сравнения двух моделей: средняя абсолютная ошибка, средняя взвешенная ошибка и коэффициент неравенства Тейла. Таблица предполагает, что сеть была более точна, чем линейная регрессионная модель, как во входной, так и в выходной выборках. Сеть сокращала ошибки прогноза между 13 и 25 процентами в течение периода входной выборки и на 20 - 40 процентов для прогнозов выходной выборки.

Таблица 1

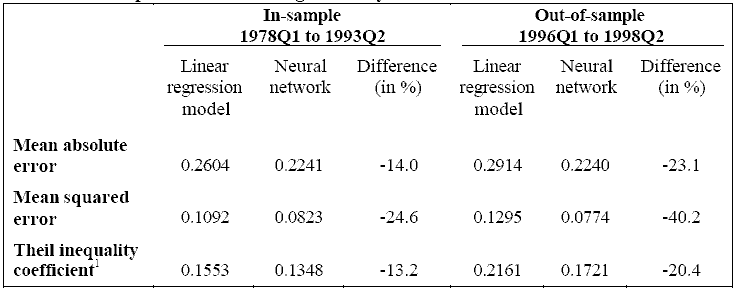
1. Коэффициент неравенства Тейла находится между 0 и 1. Значение коэффициента приближается к нолю с увеличением точности прогноза.

С теоретической точки зрения, этот результат не слишком удивителен. Учитывая, что увеличенная нейронная сеть охватывает линейную модель регрессии, сеть не должна, в теории, прогнозировать хуже, чем линейная модель. Два фактора, однако, могли повлиять на то, что сеть прогнозирует хуже, чем линейная модель. Во-первых, алгоритм оптимизации мог бы остаться захваченным на локальном минимуме, который был далеко от глобального. Чтобы избежать этой проблемы, веса сети были повторно оценены, используя 800 наборов случайных начальных значений. Сеть с наибольшей точностью в наборе проверки правильности была сохранена. Во вторых, сеть могла сверхприспособить данные, несмотря на использование рано останавливающейся процедуры. Когда число наблюдений в наборах обучения и проверки правильности является маленьким, сверхприспособление могло бы все еще происходить, используя рано останавливающуюся процедуру. Это, кажется, не происходит в данном примере, учитывая относительно хорошее прогнозирование сети выходной выборки.

Четыре статистических теста использовались, чтобы оценить, было ли усовершенствование прогнозирующей точности статистически существенно: Вилконсонский тест ранга признака, непараметрический тест признака, тест Дайболда и Мариано (1995) и тест Эшли, Гранжера и Шмаленса(1980). В каждом из этих тестов нулевая гипотеза постулирует то, что точность прогноза обеих моделей одинакова. Все тесты были двусторонними и применялись к средней взвешенной ошибке и средней абсолютной ошибке. Результаты, которые получены в итоге в Таблице 2, предполагают, что есть только ограниченное доказательство того, что усовершенствование прогнозирующей точности было статистически существенно. На 90-процентном уровне достоверности, нулевая гипотеза только могла быть отклонена в четырех или пяти из четырнадцати возможностей, представленных в таблице. Хотя точки оценки в Таблице 1 предполагают, что нейронная сеть превзошла линейную модель, стандартные отклонения тестирующей статистики были слишком большими, чтобы сделать вывод о статистически существенном усовершенствовании.

Таблица 2

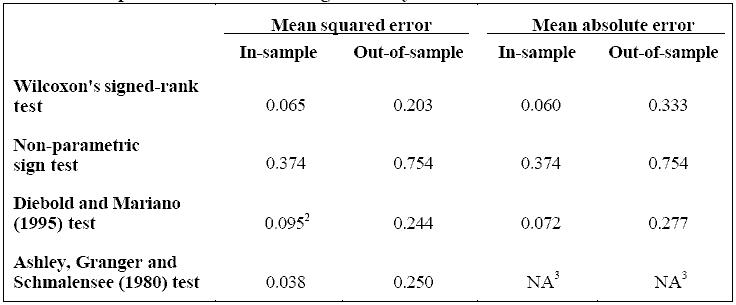
Кроме того, выполняемые прогнозирующие испытания (Чонг и Хендри, 1986), проводились для обоих периодов: входной и выходной выборок. Результаты не позволяли нам отклонить то, что никакая модель не охватывала другую. Следовательно, основываясь на всех наших испытаниях, мы не можем заключить, что усовершенствование точности прогноза статистически существенно.

Нейронная сеть, изложенная в этом разделе, должна рассматриваться как дополнение к линейной модели регрессии, а не как замена, потому что она использовала каузальные величины линейной модели как отправной точки. Хотя это может походить на тривиальный момент, фактически это очень важно. Вычислительное усилие, требуемое для проектирования нейронной сети, делает фактически невозможным строить модель с нуля, без помощи линейной регрессионной модели. Как объяснялось в Разделе 3.2 (рисунок 8), проектирование нейронной сети - длинный процесс метода проб и ошибок. Для данного набора каузальных величин и данной сетевой архитектуры, нейронная сеть должна быть повторно оценена сотни или тысячи раз с другими наборами начальных значений, чтобы избежать локального минимума (В текущем примере, для Пентиума 350 МГц потребовалось приблизительно 25 часов, чтобы повторно оценить сеть с 800 наборами начальных значений). Этот полный процесс переоценки должен быть повторен для каждой другой рассматриваемой сетевой архитектуры прежде, чем делать заключение относительно точности прогноза выходной выборки, связанной с данным набором каузальных величин. Таким образом, каждый раз, когда внесено изменение в наборе каузальных величин, сеть должна быть повторно оценена под несколькими другими архитектурами, требующими нескольких сотен или тысяч начальных значений. Этот процесс был бы слишком длинным, если бы это сопровождало документ.

В начало