Краткосрочное и среднесрочное
прогнозирование динамики ВВП
на основе модели Хикса

1. Экономические аспекты модели Хикса.
2. Краткосрочное прогнозирование.
3. Среднесрочное прогнозирование. Сценарный подход.

Так называемая модель Хикса является простейшей регрессионной моделью, описывающей динамику ВВП. В данной работе представлена попытка построения прогнозов как в краткосрочной, так и долгосрочной перспективе, уровня ВВП России. Имеющийся статистический материал позволяет делать на основе данной модели хорошие краткосрочные (глубиной в год) прогнозы. Также имеется возможность построения среднесрочных прогнозов (до 5 лет) с применением сценарного подхода.

В качестве итогового вывода работы можно утверждать, что 1998 г. явится годом начала реального роста экономики, который продолжится в течение последующих пяти лет, однако уровень ВВП 1994 года не будет достигнут.

B начало

Построение удовлетворительных прогнозов динамики ВВП является сложной и содержательной задачей. Суть проблемы состоит в следующем. Месячные данные объемов ВВП имеют четко выраженную сезонную составляющую, а также определенную цикличность. Наличие годовой сезонности связано с сезонностью в отраслях экономики и выражается в падении уровня ВВП января к прошлому декабря с постепенном ростом в течении полследующего года. Сущность циклической компоненты определяется закономерностями спадов и подъемов экономики.

Если при прогнозировании динамики ВВП годовую сезонность показателей удается хорошо учесть достаточно простыми классическими статистическими методами, то с цикличностью дело обстоит куда более сложнее. Если экономика, находящаяся в состоянии равновесия, начинает под воздействием каких-либо факторов расти, в действие вступает механизм мультипликатора-акселераторора (взаимного “подталкивания” инвестиций и доходов), который, казалось бы, должен обеспечить “вечное” процветание. Но этого не происходит: через определенное время подъем сменяется спадом, притом глубоким и продолжительным, который, однако не длится вечно, а рано или уступает место подъему.

Проблема смены тенденций экономического развития в силу понятных причин являются объектом пристального внимания зарубежных экономистов. Учитывая состояние экономики России на данный момент, в этой работе акцент будет сделан на вопросах приближения и прохождения “нижней” точки спада экономики.

В основе предлагаемого исследования лежат, главным образом, теоретические модели американского экономиста Дж. Хикса. В рамках теории цикла проводится разграничение между автономными и производными инвестициями. Первые – это та часть капиталовложений, которые осуществляются по причинам, независящим от изменения величины национального дохода (изобретения, изменения численности населения и т.п.) Производные капиталовложения, напротив, зависят от изменения национального дохода (не от абсолютных его размеров, а от величин его прироста – положительного или отрицательного). Аналогично и потребление делится на автономное (определяемое сложившимися потребительскими стандартами) и производное.

При этом предполагается, что производные инвестиции и потребление зависит от изменение дохода не в данный период (год), а с учетом таких изменений в предыдущий период, инвестиции – за предыдущие два, так как планы капиталовложений требуют времени для разработки и реализации проектов). Тогда

C_t = α + CY_t-1,
где C_t - потребление, α - автономное потребление, C - предельная склонность к потреблению, Y_t-1 - доход предыдущего периода;

I_t = b + V( Y_t-1 - Y_t-2 ), где I_t - инвестиции, b - автономные капиталовложения, V - акселератор.

Таким образом, уравнение дохода приобретает следующий вид:

Y_t = A + CY_t-1 + V( Y_t-1 - Y_t-2 ), (1) где A = α + b представляет собой автономный совокупный спрос.

Вот те экономические закономерности в динамике ВВП, постулированные Хиксом, которые будут лежать в основе данной работы.

Прежде чем непосредственно перейти к изложению полученных результатов следует рассказать об использованных статистических данных, статистической базе. Основной и единственной информацией, наличие которой предполагает данная работа, это месячные наблюдения ВВП России с января 1994 г. по ноябрь 1997 г. в сопоставимых ценах января 1994 г. Уровень ВВП в январе 1994 году следует принять за 100%, тогда величины ВВП в оставшихся месяцах будут выражены частями от этой величины. Такие данные представлены в таблице 1, причем в этой таблице рядом с данными ВВП в приведенных ценах представлены их номинальные величины.

Динамика ВВП
	ВВП (трлн.руб.)	ВВП (сопост.цены) -базисные
янв.94	28.40	100.00
февр.94	30.30	96.29
мар.94	33.10	97.94
апр.94	39.20	106.90
май.94	43.50	110.97
июн.94	50.50	121.54
июл.94	50.80	116.11
авг.94	52.70	115.15
сен.94	56.10	114.35
окт.94	69.00	122.19
ноя.94	73.00	113.30
дек.94	83.00	110.67
янв.95	76.00	86.02
февр.95	81.00	82.60
мар.95	87.00	81.47
апр.95	100.00	86.30
май.95	118.00	94.38
июн.95	138.00	103.45
июл.95	152.00	108.11
авг.95	165.00	112.19
сен.95	172.00	111.91
окт.95	179.00	111.24
ноя.95	179.00	106.45
дек.95	184.00	106.03
янв.96	157.00	86.91
февр.96	152.00	81.85
мар.96	156.00	81.71
апр.96	163.00	83.54
май.96	171.00	86.26
июн.96	178.00	88.73
июл.96	186.00	92.07
авг.96	198.00	98.21
сен.96	209.00	103.36
окт.96	219.00	107.02
ноя.96	227.00	108.86
дек.96	240.00	113.50
янв.96	157.00	86.91
февр.96	152.00	81.85
мар.96	156.00	81.71
апр.96	163.00	83.54
май.96	171.00	86.26
июн.96	178.00	88.73
июл.96	186.00	92.07
авг.96	198.00	98.21
сен.96	209.00	103.36
окт.96	219.00	107.02
ноя.96	227.00	108.86
дек.96	240.00	113.50
янв.97	202.00	93.38
февр.97	199.00	90.64
мар.97	204.00	91.63
апр.97	205.00	91.17
май.97	207.00	91.24
июн.97	215.00	93.73
июл.97	222.00	95.92
авг.97	234.00	101.21
сен.97	245.00	106.28
окт.97	240.00	103.91
ноя.97	247.00	106.30

Таблица 1

Для лучшего визуального восприятия этих данных и выявления внутренних закономерностей в динамики на графике 1 изображены временные ряды таблицы 1, причем необходимо учесть, что единицами измерения одного ряда являются трлн. руб., а другого - %.

График 1

Как видно из графиков, ряд номинальных величин ВВП неуклонно растет вверх, что очевидно, связано с наличием в статистических данных элемента инфляции. Вместе с тем в номинальном и приведенном рядах четко видно присутствие выше упомянутой годовой сезонной составляющей. С другой стороны проявление цикличности ВВП, характеризующей подъем/спад экономики, на представленных графиках не различимо. Для получения наглядного восприятия данного аспекта рассчитаем среднегодовые величины приведенного ряда ВВП. Так полученные показатели можно найти на графике 2.

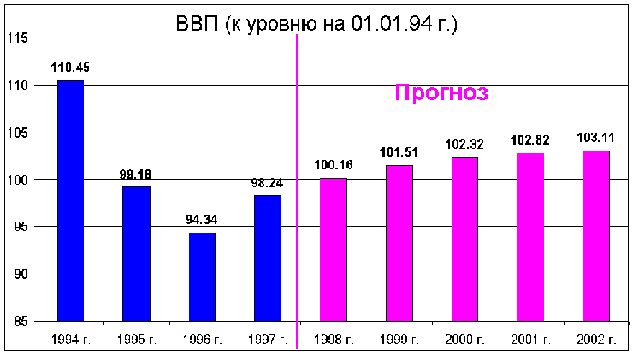
График 2

Анализ графиков позволяет говорить о наличии спада ВВП в 95, 96 гг. по сравнению с 1994 г. и некотором росте в 1997 г. То, является ли данный рост реальным, или он связан только лишь со статистическими погрешностями наблюдений, перешла ли наша экономика нижнюю точку спада, или ей это еще предстоит сделать, и что вообще будет в ближайшие 5 лет, вот те вопросы, некоторые ответы на которые будут даны в предлагаемой работе.

Как видно из таблицы 1, исходный ряд месячных уровней ВВП в сопоставимых ценах содержит всего 47 наблюдений, что, вообще говоря, достаточно мало, чтобы делать надежные статистические выводы. Тем более, мало что можно сказать, изучая годовые объемы величин, такой ряд будет состоять всего из четырех чисел. Учитывая это замечание, предлагается несколько видоизменить уравнение Хикса (1), а именно считать, что Y_t это не годовой уровень ВВП, а месячный, и разность ( Y_t-1 - Y_t-2 ) следует рассматривать не как разность между двумя соседними годами величин ВВП, а как разность между одноименными месяцами соседних лет. Тогда уравнение Хикса запишется в следующем виде:

Y_t = A + CY_t-12 + V( Y_t-1 - Y_t-24 ) + ε_t, (2)
где величины ε_t являются ошибками модели, размер которых говорит об соответствии модели реальным данным. Если величины ε_t не добавить в уравнение (2), то оно, вообще говоря, не имело бы смысла, так как указанное равенство на имеющихся статистических данных просто бы не выполнялось.

В дальнейшем, при исследовании динамики ВВП, будет удобно оперировать уравнением Хикса не в виде (2), а в несколько других эквивалентных формах.

Введем в рассмотрение ряд парных разностей месячных уровней ВВП в базисных ценах, задаваемой формулой
Δ_t = Y_t - Y_t-12 .

Тогда уравнение (2) можно переписать в виде:

Y_t = A + CY_t-12 + VΔY_t-12 + ε_t . (3)

Если в уравнении (2) раскрыть скобки и привести подобные члены, то оно перепишется как:

Y_t = A - U₁Y_t-12 U₂Y_t-24 + ε_t, (4) где U₁ = -(C+V) , U₂ = -V.

С другой стороны, если из уравнения (2) выразить переменную Y_t-12 через оставшиеся, сгруппированные особым образом, то получается еще одно эквивалентное представление соотношения (2):
Y_t-12 = C₀ + α₁Δ_t + α₂Δ_t-12 + δ_t, (5) где C₀ = A/(1-C) , α₁ = -1/(1-C), α₂ = V/(1-C) и δ_t = ε/(1-C) .

Каждое из вновь полученных уравнений (3), (4), (5) эквивалентно уравнению (3), поэтому будем именовать их также уравнениями Хикса, но каждое из них мы будем использовать в различных случаях, в зависимости от того, на какие аспекты уравнения Хикса необходимо обратить внимание.

B начало

Решение задачи краткосрочного прогнозирования динамики ВВП, где под краткосрочностью понимается построение прогноза годовой глубины, на основе уравнения Хикса может заключаться в использовании модели множественной регрессии.

Модель множественной регрессии является хорошо известной моделью статистического анализа, смысл которой заключается в попытке выразить линейным образом одну, так называемую независимую переменную ( Y ), через конечное число других переменных ( X₁ , X₂, ... , X_N ), именуемые зависимыми. При этом необходимо знать нюансы данной терминологии, называя переменные X₁ , X₂, ... , X_N зависимыми, не предполагается наличие зависимости между ними, а лишь только зависимость переменной Y от X₁ , X₂, ... , X_N . Такого рода зависимость выражается формулой Y = α₀ + α₁X₁ + α₂X₂ + ... + α_NX_N + ε , где α_i - некоторые коэффициенты, а ε - ошибка модели.

Коэффициенты α_i , вообще говоря, надо оценивать, то есть на основе имеющихся наблюдений переменных X₁ , X₂, ... , X_N , Y находятся приближенные оценки величин α_i . Классическим и наиболее популярным методом построения таких оценок является метод наименьших квадратов, хотя существует и ряд других интересных методов.

Под построением оценок параметров α_i понимается, как правило, получение не только их точечных значений (конкретных чисел), но и построение, так называемых, доверительных интервалов.

Под доверительными интервалами для параметра α_i , например под 90% доверительным интервалом, понимают такой числовой интервал, о котором можно сказать, что истинное значение параметра α_i в нем лежит с вероятностью 90%. Чем такой интервал шире, тем хуже, чем уже, тем лучше. Ширина доверительного интервала говорит о достаточности (или недостаточности) статистических данных для получения достоверных статистических выводов. В литературе часто приводят такой эмпирический факт, что для получения хоть сколько ни будь содержательных результатов необходимо иметь наблюдаемые выборки минимум объема 4(N+1). В нашем случае, что будет ясно дальше, это условие выполняется.

Как было отмечено выше, уравнение Хикса (3) можно рассматривать как уравнение множественной регрессии, в котором величина Y_t является независимой переменной, а величины Y_t-12 , Δ_t зависимыми. Рассматривая с этой точки зрения уравнения Хикса, можно получить методом наименьших квадратов точечные оценки и доверительные интервалы для параметров A, C, V. Результаты вычислений приведены в таблице 2.

	Коэффициенты	Нижние 95.0%	Верхние 95.0%	Нижние 90.0%	Верхние 90.0%
A	40.39	30.19	50.59	32.16	48.61
C	0.61	0.50	0.72	0.52	0.70
V	0.01	-0.15	0.18	-0.12	0.14

Таблица 2

Не будем пока концентрировать внимание на размерах доверительных интервалов, скажем лишь что оно допустимые, это мы сделаем в следующей главе, а обратим внимание на точечные оценки параметров.

Оценка величины автономного дохода получилась равной 40.39%, это говорит о том, что примерно 40% от уровня ВВП января 1994 г. является величиной, ниже которой ВВП упасть никогда не может.

Оценка величины предельной склонности к потреблению получилась равной 0.61, это говорит о том, что у населения примерно 60% получаемого дохода идет на потребление, а следовательно, возвращается в экономику.

Стоит отметить что оценивание параметров регрессии и построение доверительных интервалов делается в предположении адекватности регрессионной связи наблюдаемым данным. Проверить данную гипотезу можно на основе, так называемого коэффициента детерминации R² (%). О том что точно значит эта величина и как она вычисляется можно найти в статистической литературе. Принято считать, что чем она ближе к 100%, тем более адекватна регрессионная модель. В нашем случае R² =95%, что является довольно значительным показателем для принятия регрессионной модели Хикса.

После того как были получены оценки параметров множественной регрессии (3), можно построить прогноз ВВП годовой глубины. Дело в том, что значения зависимых переменных, стоящих в правой части уравнения (3), известны для t, отвечающих последним 12 месяцам, а они в свою очередь определяют значения Y_t на год вперед.

Более того, данная регрессионная модель позволяет построить не просто точечный прогноз годовой глубины, но и доверительный (75%) интервал для такого прогноза. Интервал, в границах которого наблюденные в будущем данные должны попасть с заданной вероятностью (75%). Ширина доверительного интервала говорит опять же о достаточности (или недостаточности) статистических данных для получения надежных выводов. Результаты реальных расчетов приведены в таблице 3, а на графике 3 дана их визуализация.

	ВВП к 100% на 01.01.94	min (75%)	max (75%)	Прогноз
янв.94	100.00
февр.94	96.29
мар.94	97.94
апр.94	106.90
май.94	110.97
июн.94	121.54
июл.94	116.11
авг.94	115.15
сен.94	114.35
окт.94	122.19
ноя.94	113.30
дек.94	110.67
янв.95	86.02
февр.95	82.60
мар.95	81.47
апр.95	86.30
май.95	94.38
июн.95	103.45
июл.95	108.11
авг.95	112.19
сен.95	111.91
окт.95	111.24
ноя.95	106.45
дек.95	106.03
янв.96	86.91			85.01156
февр.96	81.85			84.00448
мар.96	81.71			82.21163
апр.96	83.54			81.74191
май.96	86.26			86.49027
июн.96	88.73			88.77383
июл.96	92.07			95.4596
авг.96	98.21			99.38997
сен.96	103.36			99.56482
окт.96	107.02			110.1453
ноя.96	108.86			108.5766
дек.96	113.50			109.6491
янв.97	93.38			93.39
февр.97	90.64			90.30
мар.97	91.63			90.22
апр.97	91.17			91.34
май.97	91.24			92.99
июн.97	93.73			94.50
июл.97	95.92			96.54
авг.97	101.21			100.28
сен.97	106.28			103.42
окт.97	103.91			105.65
ноя.97	106.30			106.78
Прогноз
дек.97		107.2017	112.20168	109.7017
янв.98		93.83901	100.99901	97.41901
февр.98		90.9818	100.5518	95.7668
мар.98		93.28972	99.479721	96.38472
апр.98		91.40467	100.75467	96.07967
май.98		91.19483	100.99483	96.09483
июн.98		93.21209	102.02209	97.61709
июл.98		95.10551	102.77551	98.94051
авг.98		98.38655	105.92655	102.1566
сен.98		101.7625	108.7425	105.2525
окт.98		100.384	107.10403	103.744
ноя.98		101.6774	108.73742	105.2074

Таблица 3


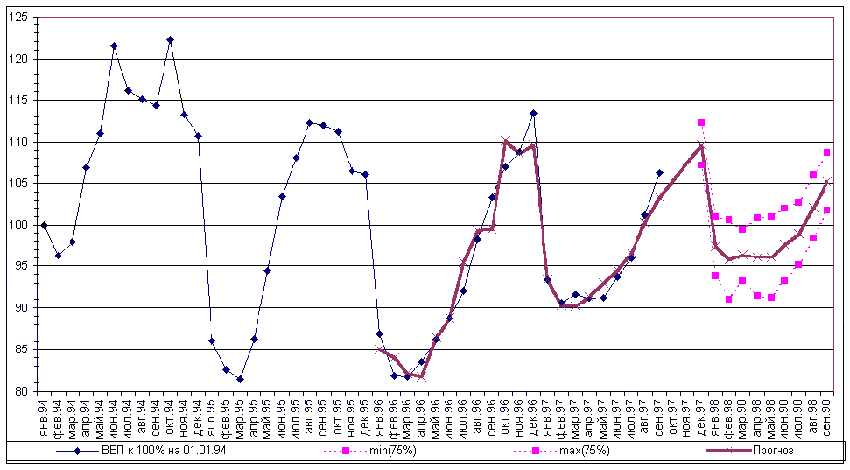
График 3

На графике наиболее жирной линией изображен прогноз ВВП с января 1996 г. по ноябрь 1998 г., где прогноз с января 1996 г. по декабрь 1997 г. рассчитан по “старым” наблюдениям зависимых переменных, а с января 1997 г. но ноябрь 1998 г. по “свежим” наблюдениям. Построенный прогноз по старым данным позволяет еще раз сравнить, то насколько адекватна построенная модель реальности. С другой стороны изображенный на графике доверительный интервал прогноза на будущее достаточно узок, чтобы говорить о достаточности статистических данных для получения определенных выводов. Так, например, из анализа графиков следует реальность экономического роста в 1998 г.

Вот те результаты, которые можно получить, базируясь на модели Хикса в плане краткосрочного прогнозирования динамики ВВП.

B начало

Задача построения среднесрочного прогноза динамики ВВП принципиально отличается от ее краткосрочного прогнозирования. Под среднесрочным понимается прогноз глубиной 5 лет. Дело в том, что если при краткосрочном прогнозировании имеющейся статистической информации достаточно для построения надежного точечного прогноза, то в среднесрочной перспективе ее не хватает. Поэтому приходится ограничиться при прогнозировании, так называемым, сценарным подходом, кокда формулируется набор сценариев развития экономики и оцениваются вероятности их реализаций.

Не вдаваясь в математико-статистические аспекты данной задачи, можно сделать следующий вывод. Если модель Хикса адекватна, то уровень ВВП в среднегодовом выражении будет стремиться к C₀ = A/(1-C) (такую величину резонно назвать предельным доходом). Сформулируем следующие 5 сценариев развития экономики:

1. Будет происходить дальнейший спад ВВП ( C₀ <= 98 ).
2. ВВП стабилизируется на достигнутом уровне ( 98< C₀ <= 102 ).
3. Произойдет дальнейший некоторый небольшой рост ВВП, но уровень ВВП 1994 г. будет все еще недостижим ( 102< C₀ <= 107 ).
4. Уровень ВВП приблизится к показателю 1994 г. ( 107< C₀ <= 110 ).
5. Уровень ВВП превысит показатель 1994 г. ( C ₀ > 110 ).

На графике 4 изображены вероятности реализации этих сценариев. Видно, что наиболее вероятен 3 сценарий. На графике 2 представлен точечный прогноз для наиболее вероятного сценария.

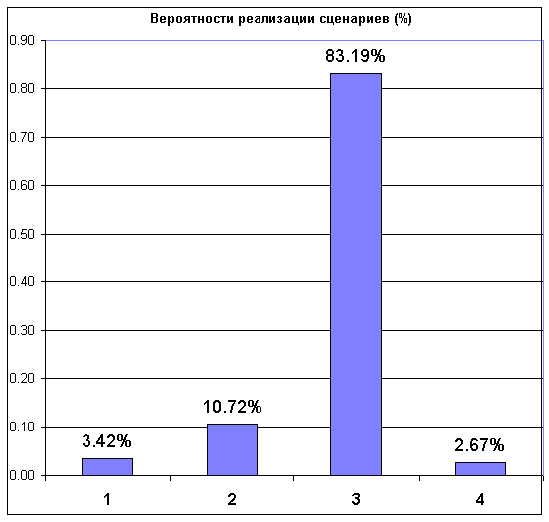
График 4

B начало