Применение искусственных нейронных сетей для решения задач управления
нейросетевых компонентов систем управления",
Диссертация на соискание ученой степени кандидата
технических наук по специальности 05.13.06 —
автоматизированные системы управления и
прогрессивные информационные технологии, —
Харьков, ХГПУ, —1998 г.
В истории развития теории автоматического управления четко
выделяются три этапа. По классификации, приведенной в [1], первым был этап
классической детерминированной теории автоматического регулирования, охвативший
период времени с конца XIX по 40-е годы XX века. В этот период основными
задачами управления были задача устойчивости и задача о качестве переходных
процессов. Второй этап теории управления начался в 40—50-х годах нашего века и
длился примерно до середины 70-х годов. Это — этап классической
стохастической теории автоматического регулирования. Он характеризуется новой
постановкой основной задачи теории управления: учесть случайные возмущения,
действующие на систему, и обеспечить хорошую работу в условиях постоянно
действующих помех.
Около 25-и лет назад в развитии теории автоматического управления начался новый этап, связанный с адаптивной постановкой основной задачи управления. Ее особенность состоит в отсутствии изначальных знаний о математической модели объекта управления, будь то дифференциальные уравнения или плотности вероятностей случайных внешних воздействий. Объект —это черный ящик, подвергающийся неизвестным случайным воздействиям. Нам доступны только его входы и выходы. Цель системы управления (СУ) состоит в том, чтобы уже в процессе функционирования определить закон регулирования, обеспечивающий оптимальное поведение объекта. Для решения этой задачи в дополнение к основному контуру в систему управления вводится контур адаптации (см. рис. 1).
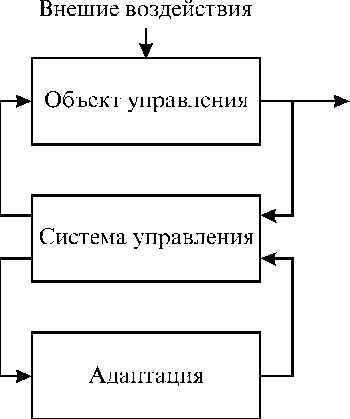
Рис. 1
Общая схема адаптивной системы управления
С самого начала третьего этапа огромное внимание уделялось адаптивному управлению линейными стационарными объектами с неизвестными параметрами (например, широко используемые методики, опирающиеся на построение наблюдателей). В рамках этого подхода в 80-х годах началось использование ИНС для решения задач управления. Полученные результаты показали, что ИНС представляют собой на просто новую методику в теории автоматического управления, а целую парадигму. Для нового направления в теории управления Вербосом было введено отдельное название —нейроуправление (neurocontrol) [2].
О цельности (парадигмоидальности) нейроуправления говорит то, что в нем, благодаря описанным выше свойствам ИНС, общим для различных нелинейных динамических объектов образом решаются задачи идентификации, синтеза систем управления, их анализа и аппаратной реализации. Результаты, полученные с применением ИНС в рамках адаптивной постановки основной задачи теории управления, легко могут использоваться и классическими подходами.
На рис. 2 представлена некоторая динамическая система (объект управления). В адаптивной постановке объект управления описывается своей функциональной моделью:
 , (1)
, (1)
связывающей вектор входных воздействий u(t) с вектором выходных сигналов y(t). Такое описание берет свое начало от идеи “черного ящика” и не является портретом динамического поведения объекта, а отражает только его функциональные связи.
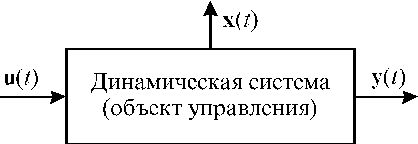
Рис. 2
Динамическая система
Введем векторы u(t)=(u1(t),u2(t),...,up(t))T, x(t)=(x1(t),x2(t),...,xn(t))T и y(t)=(y1(t),y2(t),...,ym(t))T. Здесь ui(t) и yi(t) — вход и выход системы, соответственно, xi(t) — переменная состояния системы, p — размерность входного пространства, m — размерность выходного пространства, а n — порядок системы.
Классически, динамика такой системы описывается системой дифференциальных уравнений:
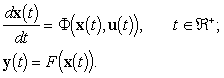 (2)
(2)
Здесь вектора функции F =(f 1, f 2,...,
f n) и F=(f1,f2,...,fm) —
статические нелинейные преобразования. ,
, 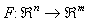 .
Вектор x(t) описывает состояние системы в момент времени t.
Он определяется состоянием системы в начальный момент t0<t
и входом u, определенном на интервале [t0,t).
Выход системы y(t) полностью определяется состоянием системы x
в момент t.
.
Вектор x(t) описывает состояние системы в момент времени t.
Он определяется состоянием системы в начальный момент t0<t
и входом u, определенном на интервале [t0,t).
Выход системы y(t) полностью определяется состоянием системы x
в момент t.
Другим подходом является дискретное описание динамической системы. Введем разбиение по времени t0,t1,t2,...., где ti+1=ti+D t, и обозначим x(tk), y(tk) и u(tk) как x(k), y(k) и u(k), соответственно. Тогда динамику системы можно описать следующими разностными уравнениями:
 (3)
(3)
Здесь F и F аналогичны преобразованиям в (2).
Уравнения (2, 3) представляют динамику системы, как преобразование вход-выход. Для широкого класса задач эти формы представления равнозначны и могут быть сведены друг к другу. Однако, при описании систем управления с нейросетевыми элементами более удобным является дискретное представление объекта управления, поэтому в дальнейшем будем рассматривать динамические, представленные в виде (3). Тем не менее, результаты, полученные для дискретного описания, могут быть распространены и на непрерывный случай.
Идентификация.
Задача идентификации является фундаментальной в теории систем и,
в частности, теории автоматического управления. Целью идентификации является
построение идентификационной модели 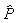 (см.
рис. 3), аппроксимирующей объект P:
(см.
рис. 3), аппроксимирующей объект P:
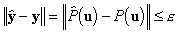 ,
,  ,
(4)
,
(4)
для некоторого заданного e >0 и определенной нормы 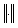 .
Здесь
.
Здесь 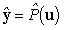 — выход идентификационной модели, U —
допустимое множество управления. Причем, как для статической, так и для
динамической систем оператор P неявно определен парами сигналов
вход-выход
— выход идентификационной модели, U —
допустимое множество управления. Причем, как для статической, так и для
динамической систем оператор P неявно определен парами сигналов
вход-выход 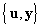 .
.

Рис. 3
Идентификация объекта управления
Выбор класса, к которому принадлежит оператор 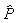 ,
и самого оператора определяется множеством факторов, связанных с требуемой
точностью и аналитической трактуемостью модели. К ним относятся адекватность
представления P с помощью
,
и самого оператора определяется множеством факторов, связанных с требуемой
точностью и аналитической трактуемостью модели. К ним относятся адекватность
представления P с помощью 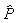 , сложность
идентификации, простота модели, возможность ее расширения и дополнения, а также
возможность использования модели в реальном масштабе времени. Выбор
, сложность
идентификации, простота модели, возможность ее расширения и дополнения, а также
возможность использования модели в реальном масштабе времени. Выбор 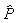 зависит
и от имеющейся априорной информацией о структуре объекта.
зависит
и от имеющейся априорной информацией о структуре объекта.
Благодаря своим универсальным аппроксимирующим свойствам, ИНС представляют собой мощный инструмент для решения задачи идентификации нелинейных статических и динамических объектов управления. Основанные на ИНС дискретные идентификационные модели называются нейроэмуляторами (НЭ) или предикторами. В общем виде они описываются следующим нелинейным уравнением:
 , (5)
, (5)
где NN(Ч ) — преобразование вход-выход, выполняемое ИНС,
l1 — глубина задержки обратной связи по выходу НЭ,
l2 — глубина задержки по входу НЭ.
Различают одношаговые и краткосрочные предикторы (эмуляторы) (см. рис. 4). Одношаговый предиктор осуществляет предсказание выходного вектора объекта по его предыстории на один шаг вперед:
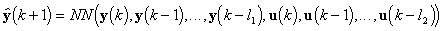 . (6)
. (6)
Такие модели объектов не является полными и используются только для прогнозирования поведения сложных систем.
Краткосрочные предикторы или просто нейроэмуляторы (5) являются полной моделью объекта в том смысле, что они могут использоваться независимо от самого объекта. С их помощью можно строить прогноз на несколько шагов вперед, отталкиваясь от сделанных ранее предсказаний. Тем не менее, само название краткосрочных предикторов подчеркивает, что глубина их предсказания является ограниченной. Нарастание ошибок, вызванных неточностью аппроксимации, со временем приводит к полному расхождению объекта и модели.

а)
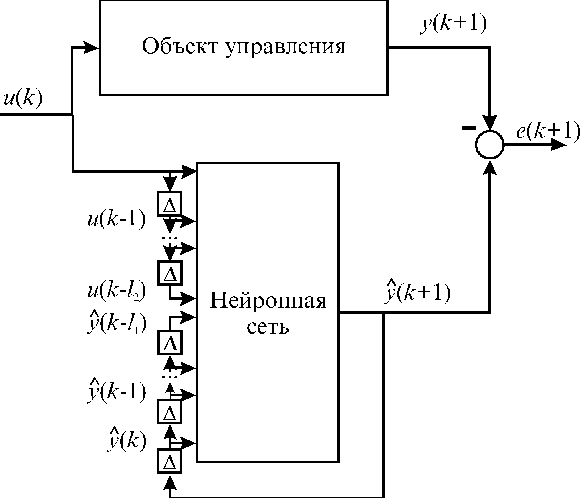
б)
Рис. 4
Типы нейросетевых идентификационных моделей.
а) — одношаговый предиктор; б) — нейроэмулятор
Долгосрочный предиктор представляет собой предельный случай, который может быть получен лишь в том случае, если идентификация объекта проводилась с учетом всех возможных его состояний, и ошибка аппроксимации равна нулю.
Классически идентификация проводится на основании определенных гипотез и теоретических исследований по имеющимся экспериментальным данным. При этом особое внимание уделяется физическому смыслу полученной модели. Конечно, полученная с помощью ИНС идентификационная модель мало пригодна для дальнейшего анализа с целью выяснить суть происходящих внутри объекта процессов. Это связано с распределенностью проводимого ею преобразования вход-выход по всем нейронам сети. Однако отражение физической сути процессов и не является необходимым условием идентификации, так как в адаптивной постанове задача состоит в другом. Цель идентификации — оперативное построении прогноза поведения объекта при определенной стратегии управления.
Управление.
Предмет теории управления составляют анализ и синтез динамических систем, в которых изменение одной или нескольких переменных ограничивается в определенных пределах. Если функции F и F в (3) известны, то задачей управления является синтез контроллера, который формирует желаемый вход u(k), основываясь на информации, доступной в момент времени tk.
В классической теории управления имеется множество хорошо разработанных методов синтеза контроллеров в частотной и временной областях для линейных систем типа:
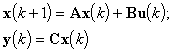 (7)
(7)
с известными матрицами A(n,n), B(n,p), C(m,n). Однако, для случая нелинейных систем, даже если F (Ч) и F(Ч) определены, единых подходов с гарантированным результатом не существует.
Использование ИНС позволяет решать задачу управления нелинейным объектом путем создания адаптивной СУ с обучаемым нейроконтроллером (НК). Здесь под обучением подразумевается процесс выработки в СУ желаемой реакции на внешние сигналы путем многократных воздействий на систему и внешней корректировки. Внешняя корректировка осуществляется “учителем”, которому известна желаемая реакция СУ на определенные воздействия. Таким образом, при обучении “учитель” сообщает системе дополнительную информацию о том, верна или неверна ее реакция (см. рис. 5).
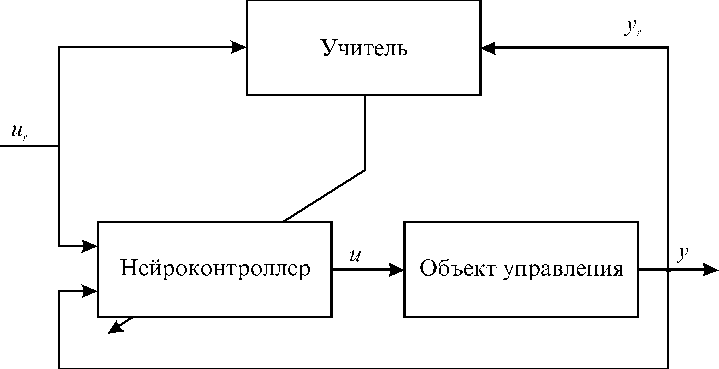
Рис. 5
Общая схема системы управления с обучаемым нейроконтроллером
При адаптации обучение используется для получения информации о состоянии и характеристиках СУ, необходимой для оптимального управления в условиях неопределенности. По существу, адаптацию можно отождествить с оптимизацией в условиях недостаточной априорной информации [3].
Существует множество подходов к применению ИНС в качестве НК. Так в работе [4] предлагается использовать ИНС, как нелинейные усилители при интегральной, дифференциальной и пропорциональной частях ПИД-контроллера (рис. 6).

Рис. 6
Система управления с комбинированным ПИД-нейроконтроллером
В тоже время в [5] (одной из первых статей по нейроуправлению) используется дискретная СУ с НК, получающим на вход сигнал управления системой ur(k) и задержанные несколько раз сигналы с выхода объекта управления. В общем случае НК такого типа может получать и задержанные сигналы со своего выхода (рис. 7). Таким образом, он формирует управляющее воздействие по следующему закону:
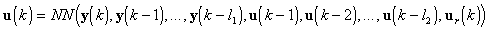 , (8)
, (8)
где l1 и l2 — глубины задержек обратных связей по выходу и входу объекта управления, соответственно.
Если первый тип СУ с ИНС является компромиссным решением в рамках классического подхода, то второй тип построен только на ИНС.
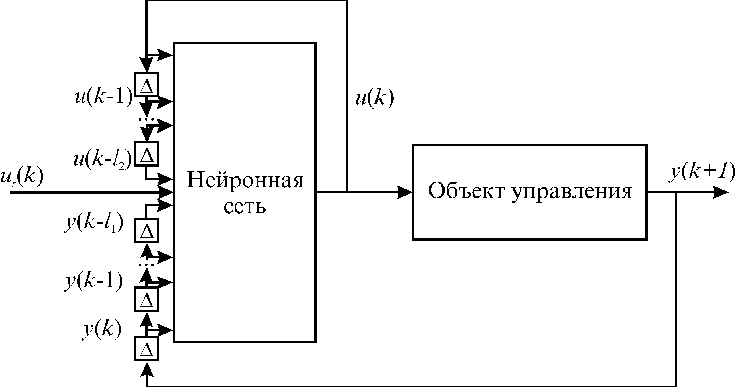
Рис. 7
Система управления с нейроконтроллером
СУ с ИНС можно классифицировать как адаптивные системы [6]. В этом случае выделяются замкнутые и разомкнутые адаптивные СУ. Под замкнутостью СУ понимается прямое использование входных и выходных сигналов объекта для адаптации управления, без промежуточной идентификации объекта. Наиболее часто используются замкнутые нейросетевые системы управления (НСУ) с эталонной моделью (рис. 8) [7].

Рис. 8
Нейросетевая система управления с эталонной моделью
Пусть имеется определенная эталонная модель СУ:
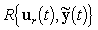 , (9)
, (9)
где ur(t) — вектор входных сигналов системы,
 — ее желаемый выход.
— ее желаемый выход.
Тогда целью обучения НК является получение ограниченного управления u(t) для tі 0 такого, что
 . (10)
. (10)
В этом случае объект будет отслеживать желаемую траекторию, определенную эталонной моделью [8]. В [9] показано, что возможно построение адаптивного НК на базе ИНС с контролируемым обучением, обеспечивающего СУ глобальную асимптотическую устойчивость.
Необходимым условием функционирования СУ с эталонной моделью является правильный выбор тестовых входных воздействий ur, так как от типа тестового сигнала зависит точность настройки основной системы на эталонную модель.
Другим распространенным типом являются замкнутые СУ без эталонной модели (рис. 9).

Рис. 9
Нейросетевая система управления с экстремальным законом управления
Целью обучения НК в них является получение закона управления, обеспечивающего заданное (обычно экстремальное) значение некоторого функционала качества I, определяемого текущим состоянием системы.
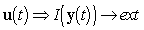 . (11)
. (11)
Существуют также схемы разомкнутых адаптивных НСУ с НЭ объекта управления. В этом случае НЭ может использоваться либо для оценки требуемого сигнала управления при заданном выходном состоянии объекта (если НЭ описывает обратную динамику объекта управления [7]), либо для оценки значений недоступных непосредственному измерению параметров объекта a [10, 11]. Эти данные используются затем для обучения НК (см. рис. 10).
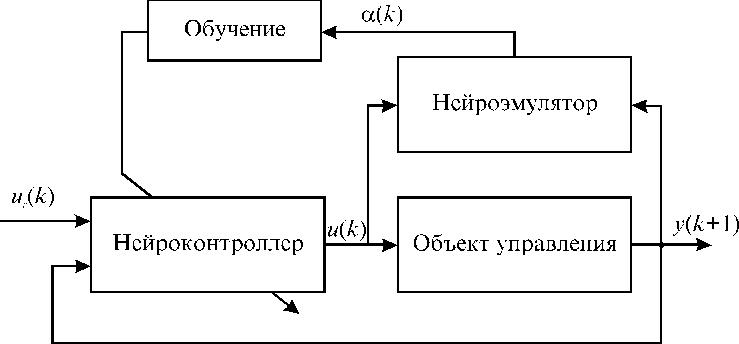
Рис. 10
Нейросетевая система управления с нейроэмулятором
Список использованных источников:
- Неймарк Ю. И., Коган Н. Я., Савельев В. П. Динамические модели теории управления. — М.: Наука, Главная редакция физико-математической литературы, 1985. —400 с.
- Werbos P. J. Backpropagation and neurocontrol: A review and prospectus // Proc. of International Joint Conf. On Neural Networks. — Vol. 1. — Washington, DC. — 1989. — P. 209—216.
- Цыпкин Я. З. Адаптация и обучение в автоматических системах. — М.: Наука, 1968. — 400 с.
- Jones A. H. Genetic Tuning Of Non-Linear PID Controllers // Artificial Neural Nets and Genetic Algorithms. Proceedings of the International Conference in Ales, France, 1995 (D. W. Pearson, N. C. Steele, R. F. Albrecht, eds.). — Wien: Springer Verlag, 1995. — P. 412—415.
- Nguyen D. H., Widrow B. Neural networks for self-learning control systems // IEEE Control Systems Magazine. — 1990. — Vol. 10. — No. 3. — P. 334—341.
- Шульце К.-П., Реберг К.-Ю. Инженерный анализ адаптивных систем: Пер. с нем. — М.: Мир, 1992. — 280 с.
- Kuntanapreeda S., Gundersen R. W., Fullmer R. R. Neural Network Model Reference Control of Nonlinear Systems // Proc. Of Int. Joint Conf. on Neural Networks. — Vol. II. — Baltimore, Maryland. — 1992. — P. 94—99.
- Narendra K. S., Annaswamy A. M. Stable Adaptive Systems. — Englewood Cliffs, NJ: Prentice-Hall, 1989. —236 p.
- Narendra K.S., Parthasarathy K. Identification and Control of Dynamical Systems Using Neural Networks // IEEE Transactions on Neural Networks. — 1990. — Vol. 1. — No. 1. — P. 4—27.
- Palis F., Schmied Th., Skljarenko E. A. Fuzzy and Neurocontrol of Drive Systems with changing Parameters and Load // Труды конференции с международным участием “Проблемы автоматизированного электропривода”. — Харьков: Основа. — 1995, С. 116—119.
- Kuan A., Bavarian B. Compensation of Unmodeled Friction in Manipulators using Neural Networks // Proc. Of Int. Joint Conf. on Neural Network. — Vol. II. — Baltimore, Maryland. — 1992. — P. 817—822.