Перевод с английского языка Филатова А.Ю.
Источник:
S.Gil, J.Deferrari. "Generalized Model of Prediction of Natural Gas Consumption"
C.Джил, Дж.Деферрари
Обобщенная Модель Предсказания Потребления Природного газа
Мы представляем модель, предназначенную для предсказания, главным образом, потребления природного газа населением и коммерческого потребления в городах для краткосрочных и среднесрочных периодов времени. В краткосрочном периоде модель успешно использовалась, чтобы предсказать ежедневное потребление газа крупных городов Аргентины. Она способна предсказать потребление 1-5 дней заранее с 10% ошибкой. В среднесрочном периоде (1-5 лет) модель позволяет нам оценить ежегодное пиковое потребление, факторы загрузки и оптимальную способность транспортировки для данной области интереса. Мы также представляем новую процедуру, чтобы получить распределение суточного потребления от ежемесячного потребления, полученного от ежемесячного составления счетов.
Введение
Предсказание потребления природного газа является критическим для газовых распределительных компании и компаний транспортировки, а также для правительственных организаций, относящихся к отрасли природного газа. В частности краткосрочный прогноз , 1-5 дней, является важным для гарантирования нормального снабжения природным газом данного города или сообщества. Этот тип предсказания особенно важен для таких стран, как Аргентина, где участки производства далеки от главных центров потребления. В случае Аргентины эти расстояния приблизительно 2000км. Это обстоятельство и нехватка больших хранилищ заставляет развивать надежные модели предсказания потребления газа вперед на несколько дней. Существующие исследования занимаются исключительно проблемой жилого, коммерческого потребления природного газа и Natural Gas Vehicle Service Stations (NGV-SS) – станций транспортировки природного газа, у которых есть непрерывные газовые услуги (договор с фирмой). Большинство больших отраслей промышленности и электрических станций в Аргентине имеют прерываемые контракты. Поэтому модели их потребления отличны от непрерывного компонента и не будет обсуждены в этой статье. Мы будем использовать термин непрерывного для указания этого типа компоненты потребления.
Есть также потребность предсказать устойчивый компонент потребления в среднесрочном периоде, в течение 1-4 лет, чтобы приспосабливать и модернизировать инфраструктуру транспортировки и распределения. Этот тип предсказания также полезен для всех отраслей газовой промышленности, которая должна планировать их производство и оптимизировать их ожидаемую закупку.
Самые важные факторы, которые затрагивают газовое потребление населения и коммерческих потребителей - температура, день недели и преобладающий сценарий потребления. Другие факторы, которые могут также влиять на потребление: скорость ветра и его направление, влажность и т.д. Из-за нехватки надежной информация относительно этих параметров, мы не включили их в нашу модель.
Есть несколько подходов предсказать ежедневное потребление природного газа, основанное на различных методах. Традиционно они были основаны на понятии уровень отопления дня, множественной линейной регрессии и эконометрические подходы, позже стали базироваться на Искусственной Нейронной Сети.
здесь
представлены основные особенности простой модели к выполнению краткосрочного
предсказания и его обобщение для среднесрочного периода. В соответствии с
критерием сбережения модель имеет в основном 6 параметров, которые являются
легкими в получении и физической интерпретации. Этот подход позволяет нам
развивать новую формализацию, чтобы получить главные параметры модели из ежемесячного
потребления. Эта особенность модели позволяет нам выводить ежедневное
распределение потребления, основанного на ежемесячном потреблении. Эта
ассоциация важна, не только потому, что ежемесячное потребление - часто
известная информация, доступная от составления актов, но также и потому, что
это позволяет нам лучше определять параметры модели и получить факторы нагрузки
для различных типов или сегментов потребителей. Кроме того, так как информация
от составления счетов часто известна для различных типов потребители, то есть
жилой, коммерческие организации и т.д., возможно получить ежедневное
распределение потребления для каждого типа потребителя. Факторы нагрузки -
важные параметры, чтобы определить стоимость транспортировки природного газа
для различных типов потребителей. Часто стоимость транспортировки вычислена для
данной доли или типa
потребителя ![]() (i–население, коммерческие
организации и т.д.):
(i–население, коммерческие
организации и т.д.):
 (1)
(1)
Здесь, Co и A - две константы, которые являются характерными для системы рассмотрения, и LFi – Фактор Изменения Нагрузки, связанный со специфической долей потребления. Это определено как отношение ежедневного (ежегодного) среднего объема потребления (Q (i)) к максимальному суточному потреблению в течение того года Qmax (i), то есть

Поэтому определение этих факторов является критическим для нескольких секторов газовой промышленности.
Наконец, существующая модель может использоваться как первое приближение предсказания потребления, на которое более сложные подходы могут быть легко применены для улучшения его точности. Таким образом, в этом исследовании мы представляем основные характеристики модели, которую мы развили для случая крупных городов Аргентины. Сначала мы опишем модель для краткосрочного периода, чтобы предсказать устойчивый компонент потребления, и сравним результат модели с наблюдаемыми значениями. Далее представляется расширение модели к среднесрочному периоду. Мы применяем эту модель, чтобы предсказать максимальное ежегодное потребление. Мы также рассматриваем новую процедуру получения ежедневного распределения потребления, используя ежемесячное потребление, полученное от составления актов. Эта процедура, весьма, общая и может использоваться, чтобы получить распределение ежедневного потребления различных типов потребителей. Мы использовали устойчивый компонент потребления как исходный пункт утверждения процедуры. Наконец, в приложении мы представляем математическое обоснование предложенной процедуры.
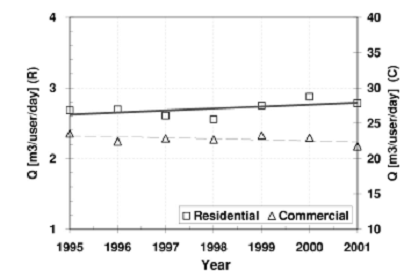
Рисунок 1 - Среднее ежегодное потребление потребителя, для жилого (R) и коммерческих (C) потребителей.
Значения, представленные здесь - средние значения ежедневного потребления в течение каждого года. Мы наблюдаем почти постоянное поведение, с небольшой уменьшающейся тенденцией. Линии соответствуют данные, полученные по выражению 3.
Привычки Потребления
В этой секции представлен результат нашего наблюдения относительно “привычки” газового потребления для Аргентины. Возможно, некоторые из этих характеристик могут быть действительными для других регионов. Однако, необходимо проверить законность этих предшествующих привычек при применении модели к новому региону интереса.
В этой работе мы сконцентрируемся, главным образом, на устойчивой компоненте потребления населения, коммерческих потребителей, маленьких отраслей промышленности и использование NGV. Стоимость природного газа в Аргентине, в период исследования 1994-2001гг., была очень устойчивым, с изменениями в порядке меньше, чем 1 % ежегодно. Среднегодовое потребление потребителей, для различных типов, в течение изученного здесь периода, было почти постоянным с небольшим линейным отклонением. Рисунок 1 иллюстрирует эту ситуацию для населения и коммерческих потребителей. Ситуация для всех регионов проанализирована и другие типы потребителей показывают подобную тенденцию. Это поведение может быть описано следующим линейным выражением:
![]()
![]() -
представляет среднее ежегодное потребление потребителей, соответствуя
составляющим i (Население, Коммерческие потребители и т.д.) во время
t.
-
представляет среднее ежегодное потребление потребителей, соответствуя
составляющим i (Население, Коммерческие потребители и т.д.) во время
t. ![]() является
соответствующим значением в рекомендуемое время время to и fusr(i) является параметром,
который определяет ежегодное изменение Qusr(i).
является
соответствующим значением в рекомендуемое время время to и fusr(i) является параметром,
который определяет ежегодное изменение Qusr(i).
Рисунок 2 показывает ежегодное изменение в числе потребителей для GBA. Здесь снова находится линейное изменение в числе потребителей со временем, то есть:
![]()
где
![]() представляет
число потребителей типа (i) в течение года, обозначенного t,
N0 (i) – число потребителей типа i в течение года t0 взятого
как рекомендуемый,
представляет
число потребителей типа (i) в течение года, обозначенного t,
N0 (i) – число потребителей типа i в течение года t0 взятого
как рекомендуемый, ![]() - число лет
между t и t0. fN (i) - фактор, который описывает
увеличение числа потребителей типа (i) для рассматриваемой области. Параметры
N0 (i) и fN (i), так же как Qusr0 (i) и fusr (i) могут быть получены от наменьшего
квадратичного отклонения данных.
- число лет
между t и t0. fN (i) - фактор, который описывает
увеличение числа потребителей типа (i) для рассматриваемой области. Параметры
N0 (i) и fN (i), так же как Qusr0 (i) и fusr (i) могут быть получены от наменьшего
квадратичного отклонения данных.
Комбинируя выражения (3) и (4), возможно получить полное среднее изменение потребления для каждой области и для различных типов потребителей, то есть:

где ![]() .
.
Мы также определили ![]()
![]() .
Этот параметр характеризует полное изменение в потреблении в данной области и
для специфической доли потребителей, обозначенной i. Поэтому
возможно написать полное среднее значение изменения потребления для каждой
области как:
.
Этот параметр характеризует полное изменение в потреблении в данной области и
для специфической доли потребителей, обозначенной i. Поэтому
возможно написать полное среднее значение изменения потребления для каждой
области как:
![]()
Последнее выражение будет полезно, чтобы сделать проектирования из потребления в среднесрочном периоде. Здесь в проанализированных случаях, временная зависимость потребления и числа потребителей, оказалось, было линейным. Эта специфическая зависимость - не требование для законности модели, однако, эти отношения должны быть известны.
Модель Предсказания – Краткосрочный Период
Предсказание устойчивых компонент (население, коммерческих потребителей и т.д.) потребления природного газа сделано с помощью корреляции, обычно существующей между суточным потреблением и температурой. Традиционно, понятие Ежедневный Уровень Отопления (HDD) использовался, чтобы установить такую связь. Этот параметр определен как сумма различия среднего значений почасовой температуры Ti и температуры, взятой как рекомендация Tref. Это температура изменяется для каждой области, но находится часто в пределах -18°C(65°F). Более точно, HDD определен как:
![]()
где сумма получена в течение всех часов дня, для которых Tref>Ti. Должно быть указано, что вычисление HDD требует знания температур в течение каждого часа дня. Эта информация может быть доступной по опыту, а непросто предсказанной заранее. Используя базу данных температур, соответствующую нескольким годам для нескольких городов Аргентины, было определено, что HDD чрезвычайно коррелирован со среднесуточной температурой, <T>, в течение того же самого дня. <T> определен, как среднее значение между максимумом, Tmax, и минимумом ежедневной температуры, Tmin.
Это наблюдение – очень существенно, потому что это указывает, что мы можем заменить параметр HDD на <T>, который не только менее дорогостоящий при получении и использовании, но также имеет большое преимущество, что это может быть надежно предсказано на несколько дней ранее. Этот факт также оправдывает приближение HDD=Tref-<T>.
Разработанная нами модель основана на выполнении условия, что потребители придерживаются не только текущей температуры, но также и заранее определенного графика. Это утверждение может быть подтверждено наблюдением, согласно которому, потребление газа больше для той же температуры в зимний день, чем для летнего или весеннего дня. Эта инерция – подтверждение того факта, что потребители обычно не включают их отопление, пока температура не остается низкой в течение нескольких дней. Аналогично, потребители не выключают отопление, пока увеличение температуры не удержится в течение нескольких дней. Этот эффект инерции в потреблении может быть взят в рассмотрение при представлении концепции эффективной температуры, Teff, которая определяется как линейная комбинация между значением <T> дня перед анализом и скользящим средним средней температуры (T_n) за n предыдущих дней. Обычно n изменяется в пределах 3-5. Более конкретно:
![]()
где i – представляет другие предыдущие дни: i=0 обозначает сегодня, i=-1 – вчера, i=-2 – позавчера и т.д.
![]()
Здесь w – весовой коэффициент (в пределах от 0 до 1), который найден из наиболее подходящих данных. <T> представляет значение температуры рассматриваемого дня
Значение эффективной температуры
заключается в том, что автоматически объединяются эффекты инерции или
запаздывания, которые являются характеристиками потребления природного газа.
Используя этот параметр, возможно описать отношение потребления ![]() в
сравнении с Teff с помощью функции:
в
сравнении с Teff с помощью функции:
![]()
В этом выражении, все
параметры ![]() и
и ![]() зависят
от конкретного региона объединения и типа потребителей для объединения.
Супериндекс (i) обозначает эти две ситуации.
зависят
от конкретного региона объединения и типа потребителей для объединения.
Супериндекс (i) обозначает эти две ситуации.
Для простоты мы не включаем
супериндекс в параметры ![]() , они выражены не
явно. Как можно увидеть на рисунке 4 и 5, выражение (10) предоставляет
адекватное описание данных. Значения четырех параметров, фигурирующие в
выражении (10) могут быть легко поняты. Точка изгиба на прямой, соответствующая
координатам
, они выражены не
явно. Как можно увидеть на рисунке 4 и 5, выражение (10) предоставляет
адекватное описание данных. Значения четырех параметров, фигурирующие в
выражении (10) могут быть легко поняты. Точка изгиба на прямой, соответствующая
координатам ![]() , представляет
потребление при Teff=To и
связана со средним ежегодным (ежедневным) потреблением, обговоренным выше.
Результат
, представляет
потребление при Teff=To и
связана со средним ежегодным (ежедневным) потреблением, обговоренным выше.
Результат ![]() представляет
асимптотическую разницу в потреблении между наинизшими (самыми жаркими) днями и
наивысшими (самыми холодными днями). Наше исследование показывает, как
ожидается, что параметры
представляет
асимптотическую разницу в потреблении между наинизшими (самыми жаркими) днями и
наивысшими (самыми холодными днями). Наше исследование показывает, как
ожидается, что параметры ![]() не изменяются во
времени, как характеристики жителей региона. С другой стороны, временная
зависимость, показанная выражениями (3) и (6), может быть прямо приложена к
не изменяются во
времени, как характеристики жителей региона. С другой стороны, временная
зависимость, показанная выражениями (3) и (6), может быть прямо приложена к ![]() ,
,
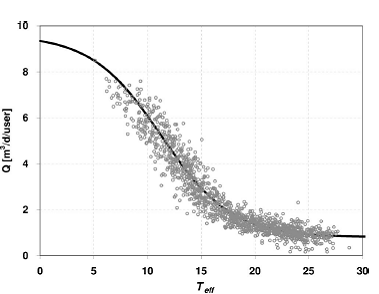
Рисунок 5 – Изменение дневной постоянной компоненты потребления, Qi, как функции эффективной температуры, Teff, для региона GBA для всех рабочих дней 1996-2000. Кружки – значения данных и прямая, полученная по данным, используя выражения (10).
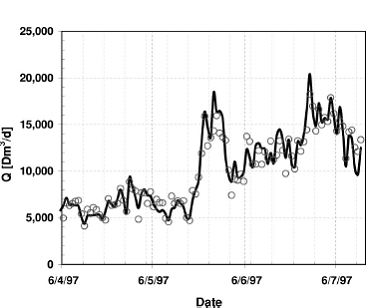
Рисунок 6 – Сравнение наблюдаемой общей постоянной потребления природного газа (незаштрихованные кружки) для региона GBA и предсказание по модели (прямая). Единица измерения вертикальной оси – 1000 м3/день. Вертикальная решетка относится к началу недели (Воскресенье).
Интервал времени, представленный на графике (с апреля по июль 1997) охватывает осень и начало зимы.
![]()
Параметр ![]() представляет
представляет ![]() или
или
![]() , зависящие от того,
как мы учитываем потребление по потребителям, эквивалентно (3) или общее
потребление региона, эквивалент (6). Таким образом, мы видим, что
представляемая модель может соединять среднесрочные изменения потребления со
временем. В действительности, наша модель может воспроизводить потребление
данного региона для периода времени, включающего 4 -7 лет с такими же
параметрами. Завершающий анализ для краткосрочного периода потребления – это
анализ выходных и праздничных дней. Из анализа данных мы можем воспроизводить
данные для большинства регионов Аргентины, используя фактор, который снижает
значение, предсказанное по модели приблизительно на 10% в пятницы и около 15% в
субботы и праздничные дни. Рисунок 6 показывает сравнение между предсказанием
по модели и наблюдаемое потребление для общей постоянной составляющей
потребления природного газа для регионов GBA. Этот тип
соглашения – образец качества подходящего найденного для большинства регионов
исследования. Мы наблюдали, что в 95% дней согласие между моделью и реальными
данными приблизительно 10%. Интересно отметить, что предсказание по этой модели
более трудоемкое, чем предсказание по температуре. Это потому что эффективная
температура зависит только частично от прогнозируемой температуры, включающей
неточности, и частично от температуры предшествующих дней, которые уже были
измерены.
, зависящие от того,
как мы учитываем потребление по потребителям, эквивалентно (3) или общее
потребление региона, эквивалент (6). Таким образом, мы видим, что
представляемая модель может соединять среднесрочные изменения потребления со
временем. В действительности, наша модель может воспроизводить потребление
данного региона для периода времени, включающего 4 -7 лет с такими же
параметрами. Завершающий анализ для краткосрочного периода потребления – это
анализ выходных и праздничных дней. Из анализа данных мы можем воспроизводить
данные для большинства регионов Аргентины, используя фактор, который снижает
значение, предсказанное по модели приблизительно на 10% в пятницы и около 15% в
субботы и праздничные дни. Рисунок 6 показывает сравнение между предсказанием
по модели и наблюдаемое потребление для общей постоянной составляющей
потребления природного газа для регионов GBA. Этот тип
соглашения – образец качества подходящего найденного для большинства регионов
исследования. Мы наблюдали, что в 95% дней согласие между моделью и реальными
данными приблизительно 10%. Интересно отметить, что предсказание по этой модели
более трудоемкое, чем предсказание по температуре. Это потому что эффективная
температура зависит только частично от прогнозируемой температуры, включающей
неточности, и частично от температуры предшествующих дней, которые уже были
измерены.
Модель Предсказания – Среднесрочный Период
В принципе модель, описанная в предыдущем разделе, может быть использована для получения среднесрочных предсказаний потребления. Однако, в соответствии с основной невозможностью получения долгосрочного прогноза температуры, на практике пригодность (применимость) такой модели ограничено от 1 года до 5 лет.
В случае газовой промышленности, чем мы обычно интересуемся – не обязательно предсказание потребления на данный день одного или двух лет, а большей вероятностью данного сценария потребления. Вероятность распределения температур для данного региона может быть получена из базы данных истории температур. В особенности, если мы имеем доступ к базе данных ежедневных максимумов и минимумов температур за 10 и более лет, то возможно получить реальное распределение будущих температур для данного региона.
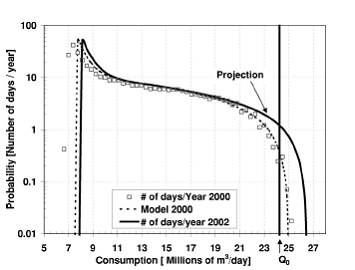
Рисунок 7 – Вероятность нахождения постоянной компоненты потребления для данного года и региона.
Горизонтальная ось представляет общее потребление в тысячах куб.м/день и вертикальная ось – вероятность, выраженная в количестве дней года, с которой данный сценарий потребления может произойти в году. Штриховая кривая – предсказание модели для года, взятого как справочный (2000), квадратные значки – наблюдаемые значения для этого года. Толстая непрерывная кривая - это предсказание по модели на будущий год.
В частности, площадь между толстой кривой и
вертикальной линией с ординатой ![]() представляет
вероятность того, что потребление в этом регионе превысит
представляет
вероятность того, что потребление в этом регионе превысит ![]() для
анализируемого года.
для
анализируемого года.
Основная причина этого утверждения в том, что
температуры, ожидаемые в ближайшем прошлом, могут также ожидаться в будущем с
той же вероятностью. Здесь мы считаем, что возможные глобальные температурные
изменения имеют незначительный эффект в рассматриваемый период времени (1 -10
лет). Этот тип глобальных изменений ожидается на уровне 1![]() в 100
лет [7]. Однако, используя исторические данные, основанные на температуре, мы
можем получить эффективную температуру для всего периода времени. Из
гистограммы частоты появления температуры мы просто можем получить вероятность
появления температуры в будущем. Комбинируя эти вероятности с моделью
предсказания, с параметрами, установленными как обсужденные в предыдущем
разделе, мы можем получить вероятность появления данного режима потребления для
любого года в ближайшем будущем. Развитие потребления со временем уже
содержится в параметре, обозначенном в выражениях (3),(4) и (6). Поэтому, мы
можем предсказать для любого региона и года в среднесрочный период вероятность
распределения потребления. На рисунке 7 мы представляем соответствующее
распределение, учитывая как справочный 2000 год и соответствующий прогноз на
2001 год. На этом рисунке мы представляем вероятность потребления, выраженную
в тысячах кубических метрах в день
в 100
лет [7]. Однако, используя исторические данные, основанные на температуре, мы
можем получить эффективную температуру для всего периода времени. Из
гистограммы частоты появления температуры мы просто можем получить вероятность
появления температуры в будущем. Комбинируя эти вероятности с моделью
предсказания, с параметрами, установленными как обсужденные в предыдущем
разделе, мы можем получить вероятность появления данного режима потребления для
любого года в ближайшем будущем. Развитие потребления со временем уже
содержится в параметре, обозначенном в выражениях (3),(4) и (6). Поэтому, мы
можем предсказать для любого региона и года в среднесрочный период вероятность
распределения потребления. На рисунке 7 мы представляем соответствующее
распределение, учитывая как справочный 2000 год и соответствующий прогноз на
2001 год. На этом рисунке мы представляем вероятность потребления, выраженную
в тысячах кубических метрах в день ![]() в период в
количественном выражении дней года, в которых потребление обозначенное на
вертикальной оси наиболее вероятно произойдет. Этот вид информации позволяет
нам оценить количество дней в данном году в будущем, для которого можно
достигнуть данного значения. Поэтому модель позволяет нам определить
оптимальное значение газа, которое может быть адекватно указанному в контракте
(резервное значение) с производителями и поставщиками. Этот тип распределения
также полезен для оценки Нагрузочного Фактора (LF),
определенного в выражении (2), так как модель позволяет нам получить и среднее
потребление <Q>, и максимальное потребление
в период в
количественном выражении дней года, в которых потребление обозначенное на
вертикальной оси наиболее вероятно произойдет. Этот вид информации позволяет
нам оценить количество дней в данном году в будущем, для которого можно
достигнуть данного значения. Поэтому модель позволяет нам определить
оптимальное значение газа, которое может быть адекватно указанному в контракте
(резервное значение) с производителями и поставщиками. Этот тип распределения
также полезен для оценки Нагрузочного Фактора (LF),
определенного в выражении (2), так как модель позволяет нам получить и среднее
потребление <Q>, и максимальное потребление ![]() для
данного года.
для
данного года.
Зависимость Между Дневным и Месячным Распределением Потребления – Факторы Нагрузки
В этом разделе мы представляем новую процедуру, которая
устанавливает связь между дневным и месячным распределением потребления. Эта
связь позволяет оценить факторы нагрузки с помощью информации, полученной из
ежемесячных актов. Более того, эта процедура позволяет получит факторы нагрузки
для разных типов потребителей в данном регионе. Математическая модель описания
теории, предложенная здесь, основана на предположении, что суточное потребление
природного газа может быть описано моделью, зависящей от температуры, как
описано в выражении (10). Мы также предполагаем, что каждый месяц в году значения
температур имеют вероятностное распределение, которое хорошо аппроксимируется
нормальным распределением, со средним значением, Tmonth,
зависящим от месяца года, и средним отклонением, ![]() , которое также
может зависеть от рассматриваемого месяца. На рисунке 8 представлена
гистограмма средних дневных температур для июля GBA,
использующая данные о наблюдаемых температурах для этого месяца с 1944 по 2000.
на рисунке также обозначено соответствующее нормально распределение. Можно
увидеть, что нормальное распределение близко приближено к реальным данным. Это
соглашение сохраняется для всех месяцев года. На рисунке 10 представлено
распределение среднего значения, Tmonth, как функции месяца для GBA, используя
подобную базу данных как на рисунке 9. Полоса ошибки на графике представляет
значение среднего отклонения,
, которое также
может зависеть от рассматриваемого месяца. На рисунке 8 представлена
гистограмма средних дневных температур для июля GBA,
использующая данные о наблюдаемых температурах для этого месяца с 1944 по 2000.
на рисунке также обозначено соответствующее нормально распределение. Можно
увидеть, что нормальное распределение близко приближено к реальным данным. Это
соглашение сохраняется для всех месяцев года. На рисунке 10 представлено
распределение среднего значения, Tmonth, как функции месяца для GBA, используя
подобную базу данных как на рисунке 9. Полоса ошибки на графике представляет
значение среднего отклонения, ![]() . В этом случае,
. В этом случае, ![]() было
практически постоянным (
было
практически постоянным (![]() ).
).
Если используем эффективную температуру вместо средних температур для описания месячного распределения температуры, получим такой же результат. Таким образом, все результаты, рассмотренные здесь могут быть применены к обоим распределениям: среднесуточному и эффективной температуры.
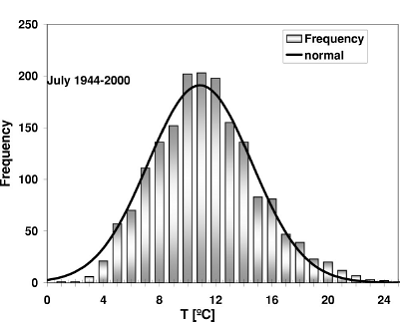
Рисунок 8 – Распределение среднесуточной температуры для июля GBA.
Алгоритм: если ежедневное потребление газа описывается
моделью, представленной в выражении (10) и среднесуточные температуры хорошо
аппроксимируются нормальным распределением со средним значением и средним
отклонением ![]() , тогда возможно
получить месячное потребление, представленное переменной Qmonth.
Эта величина – среднесуточное потребление за рассматриваемый месяц. Очевидно,
значение может быть получено, взяв взвешенное среднее дневного потребления Q(T) с
соответствующим нормальным весом.
, тогда возможно
получить месячное потребление, представленное переменной Qmonth.
Эта величина – среднесуточное потребление за рассматриваемый месяц. Очевидно,
значение может быть получено, взяв взвешенное среднее дневного потребления Q(T) с
соответствующим нормальным весом.

Интеграл в выражении (12) может быть просто найден, используя теорему о свертке преобразования Фурье, подробнее смотри в приложении. Результат имеет вид:
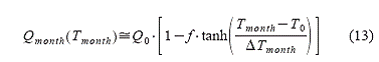
где Tmonth представляет среднюю месячную температуру и параметр ![]() ,
который определяет ширину распределения:
,
который определяет ширину распределения:
![]()
Значение Qmonth – среднее дневное потребление за месяц. Общее потребление для целого месяца будет результатом Qmonth по количеству дней в соответствующем месяце. Выражения (13) и (14) указывает, что есть связь между ежедневным распределением потребления и месячным распределением. Последняя информация может быть получена из ежемесячных актов.
Из графика зависимости Qmonth от Tmonth возможно проверить обоснованность выражения (13) и получить параметры модели (Qo, f,To,dTmonth). Один раз месячное распределение хорошо характеризовалось, используя (14) и зная дневную температуру каждого дня месяца, мы можем использовать выражение (10) для оценки распределения ежедневного потребления.
В частности, ежедневное распределение полезно для оценки максимального ежедневного потребления для данного года, Qmax, которое является важным параметром для определения фактора нагрузки каждого типа потребителей, смотри выражение (2), и оптимизирующим резервные запасы. Процедура для выполнения этой оценки следующая: из данных актов мы можем получить параметры, характеризующие выражение (13). Затем используя (14), можем получить распределение ежедневного потребления. Значение Qmax может быть вычислено из минимума эффективной температуры, Tmin, в период обучения, используя выражение:

Из информации актов за рассматриваемый период времени также возможно получить среднее ежедневное потребление, <Q>. Поэтому, используя (2) фактор нагрузки для каждого типа потребителей может быть вычислен.
В соответствии с проверкой обоснованности настоящей математической модели описания теории мы должны применить модель к случаю устойчивого потребления для региона GBA. Для этого случая общее дневное потребление берется из прямых измерений. Ежемесячное потребление и ежедневная температура также известны. Полезно обратить внимание, что когда мы берем среднюю ежемесячную температуру, результат в основном такой же, как если бы мы использовали среднюю ежедневную температуру или эффективную температуру. На рисунок 10 мы также включили модель предсказания, полученную по выражениям (13) и (14).
Фактор нагрузки, полученный по рис. 5, для
конкретного типа потребителей - ![]() . Такой же фактор
нагрузки, получается их ежемесячного распределения (рис.11) -
. Такой же фактор
нагрузки, получается их ежемесячного распределения (рис.11) - ![]() . Таким
образом, оба результата находятся в соответствии в пределах неопределенности
вычислений.
. Таким
образом, оба результата находятся в соответствии в пределах неопределенности
вычислений.
Мы выполнили второй тест настоящей математической модели описания теории для утверждения связи между ежедневным и ежемесячным распределением потребления, используя метод Монте Карло. Это очень мощная методика моделирования данных с известной вероятностью распределения. Используя наблюдаемое распределение потребления для GBA и наблюдаемое температурное распределение, мы можем производить «искусственное» ежедневное потребление с заданной уровнем дисперсии, 15% в нашем случае. Более того, эта методика позволяет нам исследовать необычные сценарии потребления, для которых мы можем не иметь действительных данных, в исследовании которых мы заинтересованы. Мы можем увидеть, что данные ежемесячного потребления схожи с предсказанием ежемесячного распределения, таким образом, подтверждая обоснованности модели.
Итак, обоснованность модели, устанавливающей связь с ежедневным и ежемесячным распределения потребления, установлена тремя процедурами:
a) математическими преобразованиями аналитического распределения, используя теорему о свертке преобразования Фурье;
b) прямым сравнением действительных данных потребления, используя постоянную потребления для случая GBA;
c) моделирование данных о потреблении по Монте Карло в применении к случаю GBA. Во всех тестах выполняются, мы имеем подтверждение обоснованности предложенной математической модели установления связи между ежедневным и ежемесячным распределениями.
Выводы
В этой работе мы представляем модель, развиваемую для предсказания потребления природного газа в краткосрочный (от 2 до 5 дней) и среднесрочный периоды (от 1 до 5 лет). Модель может быть применена для предсказания потребления различных типов потребления и также полезна для предсказания максимального потребления в среднесрочный период. Эта информация полезна как для приспособления инфраструктуры транспортировки так и для оценки оптимальных резервных запасов. Предсказания модели были успешно применены ко всем главным городам Аргентины. Предсказания краткосрочного периода схожи с исследуемым потреблением в пределах 10% -90% дней. Неопределенности среднесрочного периода предсказания находятся в пределах 12%. Эта модель может быть рассмотрена (расценена) как приближение первого порядка, в котором наиболее сложный анализ может быть сделан для улучшения его точности такой, чтобы минимизировалась корреляция отклонения данных с соблюдением предсказания модели.
Модель, представленная здесь, оказывается полезным объединением между ежедневным и ежемесячным распределением потребления. Эту связь полезна для получения, очень экономично, ежедневного распределения потребления для различных сегментов потребителей в данном регионе. А также позволяет нам оценить высшую точку потребления в среднесрочном периоде и извлечь фактор нагрузки из информации ежемесячного акта. Эта альтернатива очень привлекательна экономически, со времени ее использования не нуждается в дорогостоящих дополнительных измерениях.
Взгляды и мнения авторов, представленных здесь необязательно утверждают или отражают те из их работодателей или ENAR-GAS.
Мы хотели бы привести полезные комментарии и предложения Ing.Л.Померанца, Ing.Л.Дюперрона и доктора М.Счвинта.
Дополнение
В этом дополнении мы представляем математическое обоснование связи между ежедневным и ежемесячным распределением потребления, то есть мы выводим выражения (13) и (14) из (12).
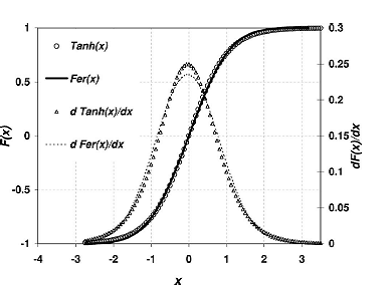
Рисунок 11 – Сравнение распределения (A3)(кружки) и (А4) непрерывная кривая относятся к левой вертикальной оси. На этом рисунке мы также показываем их соответствующие производные, относящиеся к правой вертикальной оси.
Как мы обсуждаем в этой работе, распределение потребления может быть смоделировано, используя гиперболический тангенс (выражение (10)), т.е.
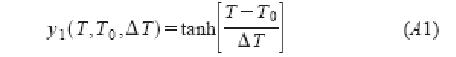
Поведение этой функции подобно функции ошибки Fer(t), определенной как [9,10]:
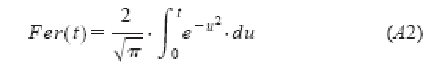
Фактически функция:
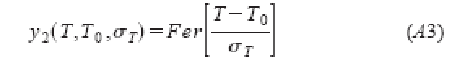
с

и
![]()
имеет очень простые характеристики функции, описанной в выражении (А1), как можно увидеть на рис.11. на этом рисунке, мы построили обе функции, относящиеся к левой оси и их производные, относящиеся к правой оси. Максимальная разница между этими функциями составляет порядка 0,04%. Поэтому функция y2(T) – хорошая аппроксимация y1(T). Действительно, каждая из этих двух функций может быть использована для моделирования распределения потребления природного газа. Наш выбор выражения (А1) был принят основе действий по усмотрению и для вычисления пригодности (удобства). Однако, для некоторых приложений может быть более подходяще использовать выражение (А2) для описания распределения потребления. В действительности, если распределение потребления может быть описано так же выражением (10) или функцией:
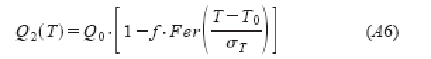
Перемещая это распределение в выражение (12), выполняя следующую замену переменных:

выражение (12) примет вид:
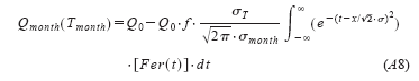
где
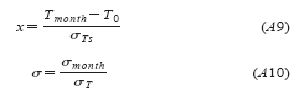
Интеграл во второй части (А8) может быть вычислен, используя метод преобразования Фурье, так как является сверткой (искривлением) Fer(t) функции с нормальным распределением. Если взять преобразование Фурье с двух сторон, используя известные свойства преобразования Фурье, получим:
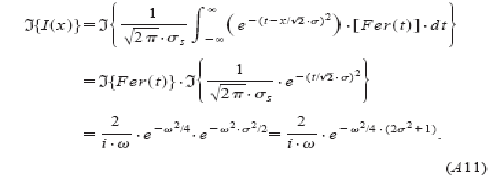

Если определим параметр ![]() как:
как:
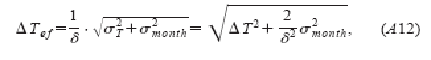
Ежемесячное распределение (12) может быть записано как:
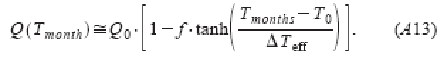
Эти два последних результата являются выражениями, которые мы хотели доказать. К тому же, если мы определим параметр φ как:
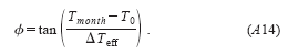
Выражение Qmonth (Tmonth) как функция от φ становится:
![]()
С этой подстановкой просто извлекать параметр из модели Qo и f для любого типа потребителей простым построением графика Qmonth как функции от φmonth. Здесь мы получаем, что другие параметры модели σmonth, ΔT и To для данного региона изучения, могут быть известны из предварительного анализа данных. Кроме того, тоже ожидается для всех типов потребителей в данном регионе.
Перевод с английского языка Филатова А.Ю.
Источник:
S.Gil, J.Deferrari. "Generalized Model of Prediction of Natural Gas Consumption"