Дегтяренко И.В. СОВРЕМЕННЫЕ МЕТОДЫ ВИБРОАКУСТИЧЕСКОЙ ДИАГНОСТИКИ МАШИН ВОЗВРАТНО-ПОСТУПАТЕЛЬНОГО ДЕЙСТВИЯ

СОВРЕМЕННЫЕ МЕТОДЫ ВИБРОАКУСТИЧЕСКОЙ ДИАГНОСТИКИ МАШИН ВОЗВРАТНО-ПОСТУПАТЕЛЬНОГО ДЕЙСТВИЯ

Дегтяренко И.В. (ДонНТУ, г. Донецк, Украина)

Приведено аналіз методів віброакустичної діагностики машин зворотно-поступальної дії, що базуються на комплексному використанні частотних та часових характеристик вібросигналів (метод частотно-часового аналізу, метод вейвлет аналізу). Висунуті пропозиції по їх подальшому розвитку з метою підвищення вірогідності діагностування.

Теория виброакустической диагностики машин возвратнопоступательного действия (МВПД) на сегодняшний день находится в стадии становления и пока не имеет устоявшихся методов диагностики, в отличие от теории виброакустической диагностики ротационных машин. Это прежде всего связано со сложным нестационарным характером процессов происходящих в МВПД, обусловленных наличием множества источников возбуждения колебаний и сложностью конструкции машины [1].

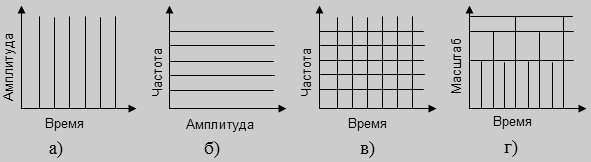
Рисунок 1 - Сравнение методов анализа вибросигналов: а) метод анализа изменения амплитуды (мощности) сигнала во времени; б) метод спектрального анализа; в) метод частотно-временного анализа; г) метод вейвлет анализа

В качестве информационных признаков о техническом состояния МВПД могут быть использованы данные о моменте появления нестационарного выброса вибросигнала, превышающего нормальный уровень, с "привязкой" к фазе рабочего цикла машины, а также данные о спектральном составе этого импульса [1,2]. Эти данные позволяют идентифицировать состояние определенного элемента МВПД. Классические методы анализа сигналов и, в частности, метод анализа изменения амплитуды или мощности вибросигнала во времени (рис. 1а) и метод спектрального анализа (рис. 1б), а так же их разновидности, не приспособлены для анализа нестационарных сигналов. При их использовании теряется информация либо о частотном составе сигнала (метод анализа изменения сигнала во времени), либо о моменте времени (фазе) возникновения того или иного импульса (метод спектрального анализа). Это не дает возможности достаточно точно идентифицировать причины возникновения отдельных компонент вибросигнала, а значит, и проводить достоверную диагностику технического состояния машины. Таким образом, актуальной задачей является обоснованный выбор и целенаправленная доработка методов анали-за нестационарных сигналов для повышения достоверности обнаружения дефектов МВПД.

Совместное извлечение временных и спектральных характеристик возможно в рамках теории частотно-временного анализа (ЧВА) [3] и вейвлет анализа [4], где для анализа нестационарных сигналов строятся функции двух переменных, представляющие сигнал одновременно во временной и частотной областях, для ЧВА (см. рис. 1в), или временной и масштабной областях для вейвлет анализа (см. рис. 1г). В теории ЧВА такие функции называются частотно-временными распределениями (ЧВР), а в теории вейвлет анализа скайлограммами (от англ. scale - масштаб).

В рамках этих теорий можно выделить несколько наиболее разработанных и применяемых на сегодняшний день методов анализа нестационарных сигналов. К ним относятся метод ЧВА с использованием ядра Цзуя-Уильямса [2,3], а также методы вейвлет анализа с использованием материнских вейвлетов Добеши и Морлета [4,5].

ЧВР Цзуя-Уильямса являет наиболее удачным, с точки зрения ми-нимизации интерференционных компонент, которые неизбежно возникают при использовании билинейных распределений [3]. Это обусловило попу-лярность использования данного распределения для решения задач диагностики машинного оборудования [2,5]. Формула для расчета данного распределения имеет вид:

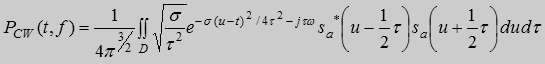где s_a(t) - аналитический сигнал анализируемого действительного сиг-нала ; * - знак комплексного сопряжения; σ - некоторая константа, изменяя значение которой, можно управлять уровнем интерференционных компонент; D - область определения сигнала s(t) .

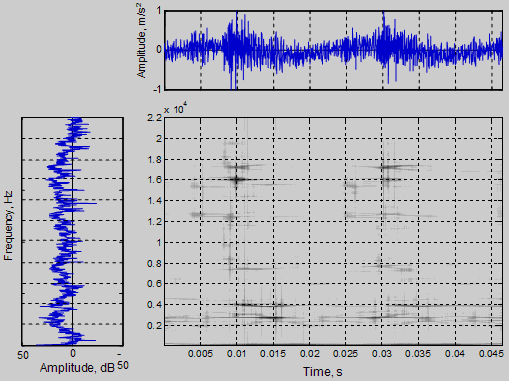
Рисунок 2 - ЧВР Цзуя-Вильямса вибросигнала поршневого компрессора

На рисунке 2 показан график ЧВР Цзуя-Уильямса для виброускоре-ния поршневого компрессора записанного на выходном патрубке (амплитуда ЧВР показана интенсивностью черного цвета). Длина реализации сигнала соответствует двум периодам работы компрессора. Анализ графика показывает, что подавляющее большинство частотно-временных ком-понент находятся в соответствии с временной реализацией и спектром сигнала, которые приведены на этом же рисунке.

Основным недостатком ЧВР Цзуя-Уильямса является его значительная избыточность, которая приводит к необходимости реализации сложных алгоритмов обработки больших объемов данных [5]. Все это определяет необходимость в значительных вычислительных ресурсах и не позволяет использовать данный метод в режиме реального времени. Кроме того, объем вычислений при увеличении количества отсчетов в обрабатываемом сегменте сигнала быстро растет, что затрудняет проведение статистической обработки ЧВР сегментов сигналов дающей возможность анализировать тонкую структуру вибросигналов.

Отчасти, недостатков, указанных для ЧВА, лишены методы вейвлет анализа [4]. В рамках данных методов нестационарный сигнал анализируется путем разложения его по принципиально новому базису представленному в виде совокупности волновых пакетов, которые характеризуется четырьмя основными принципиально важными свойствами: имеют вид коротких локализованных во времени волновых пакетов с нулевым значением интеграла; обладают возможностью сдвига по времени; способны к масштабированию (сжатию, растяжению); имеют локализованный спектр. Прямое вейвлет преобразование сигнала s(t) вычисляется по формуле

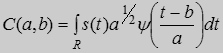где ψ(t) - функция материнского вейвлета; а - параметр, определяющий масштаб материнского вейвлета (отвечает за сжатие/растяжение вейвлета); b - параметр, задающий положение вейвлета на оси времени; R - область определения анализируемого сигнала s(t) .

Рисунок 3 - Связь временного представления вибросигнала поршневого компрессора (а) со скайлограммами на основе материнских вейвлетов Добеши 7 (б) и Морлета (в), справа показаны функции ψ(t)

Вейвлет базис может быть ортогональным, что дает возможность реконструкции сигналов и позволяет реализовать алгоритмы быстрых вейвлет-преобразований (алгоритм Малла) [4]. Примером ортогональных вейв-летов применяемых для решения задач диагностики механического оборудования являются вейвлеты Добеши [4]. Однако, существует ряд вейвлетов не обладающие свойствами ортогональности, которые, тем не менее, могут быть применены для решения задач диагностики МВПД, например вейвлеты Морлета. На рисунке 3 показана связь временной реализации виброускорения поршневого компрессора (рис. 3а) с его разложениями по вейвлетам Добеши 7-го порядка (рис. 3б) и вейвлетам Морлета (рис. 3в). Спра-ва на этом рисунке представлен вид используемых материнских функций.

Недостатками этого метода анализа является то, что необходим тщательный подбор материнского вейвлета, близкого по форме ко всем видам колебаний, возникающих в машине, что достаточно проблематично. Кроме того, при вейвлет анализе используется непривычное и физически не прозрачное разложение сигнала по масштабным коэффициентам вместо частот, что зачастую затрудняет интерпретацию результатов диагностики.

Таким образом, в статье обоснована целесообразность использова-ния методов ЧВА и вейвлет анализа для виброакустической диагностики МВПД. Кроме того показана необходимость в доработке и адаптации этих методов с целью повышения эффективности и достоверности диагностики. Для достижения этой цели необходимо

установление четких взаимосвязей между компонентами частот-но/масштабно-временных распределений и техническим состоянием эле-ментов МВПД;
уменьшение объема данных и упрощение операций обработки при проведении ЧВА вибросигналов МВПД;
корректный подбор материнских вейвлетов для анализа вибросигналов МВПД;
разработка алгоритмов выработки диагнозов о техническом со-стоянии МВПД использующих в качестве входных данных частотно-временные и масштабно-временные разложения вибросигналов.

Список литературы:

1. Воронцов А.Г., Дегтяренко И.В. Матема-тическая модель малого поршневого компрессора// Науковi працi ДонДТУ. Випуск 3. -Донецьк: ДонДТУ. -1999. -С.32-39.
Дегтяренко И.В. Об ис-пользовании ЧВА виброакустических сигналов при построении систем оценки технического состояния машин возвратно-поступательного дейст-вия// Наукові праці ДонДТУ. Випуск 12. -Донецьк: ДонДТУ. -1999. -С.47-53.
3. Коэн Л. Время-частотные распределения: Обзор // ТИИЭР. -1989. -Т. 77.- №10. -С. 72-121.
4. Дьяконов В.П. Вейвлеты. От теории к практи-ке. - М.: СОЛОН-Р, - 2002. - 448 с.
5. Pryor A.H., Mosher M., Lewicki D.G. The Application of Time-Frequency Methods to HUMS. American Helicopter Society's 57th Annual Forum,Washington D.C., May 9-11, 2001.