ОБГРУНТУВАННЯ ЗАСТОСУВАННЯ МЕТОДІВ ВЕЙВЛЕТ АНАЛІЗУ ДЛЯ ВИТЯГУ ДІАГНОСТИЧНОЇ ІНФОРМАЦІЇ З НЕСТАЦІОНАРНОЇ ВІБРАЦІЇ МАШИН ЗВОРОТНО-ПОСТУПАЛЬНОЇ ДІЇ
Дегтяренко І.В.
Донецький національний технічний університет, м. Донецьк кафедра "Автоматика та телекомунікації"
Abstract
Degtyarenko I.V. Implementation basis of wavelet analysis methods for extraction diagnostic information from reciprocating machine nonstationary vibration. The questions of using wavelet analysis methods for the reciprocation machine vibroacoustic diagnostic are discussed. Some suggestions as for development of this methods with the purpose of the diagnostic reliability increase are given.
Машини зворотно-поступальної дії (МЗПД) знайшли широке застосування в таких галузях промисловості як машинобудування, металургія, хімічна промисловість, теплоенергетика. Вони використовуються в якості елементів виконавчих пристроїв систем управління та автоматизації виробничих процесів, приводів транспортних засобів, приводів робочих органів машин та устаткування різного призначення, транспортних засобів для рідин і газів. Зокрема, до класу МЗПД відносяться: двигуни внутрішнього згоряння, побутові й промислові поршневі компресори і насоси, а також інші механічні і електромеханічні пристрої, що мають у своєму складі елементи, що рухаються поступально.
Від надійності роботи МЗПД залежать не тільки продуктивність технологічних процесів та якість цільових продуктів, але й безпека експлуатації устаткування. МЗПД є, як правило, основними споживачами енергії й сировини у виробництві. Тому забезпечення роботи цього класу машин з оптимальними техніко-економічними показниками є дуже актуальним завданням для України у світлі економії енергоносіїв, а також підвищення безпеки і якості виробництва. Рішення цього завдання неможливо без застосування засобів контролю і діагностики технічного стану машин.
Як показано в [1], одним з найбільш ефективних та широко використовуваних методів технічної діагностики механічного устаткування є метод віброакустичної діагностики. Механічні вібрації МЗПД є реакцією на неврівноважені динамічні навантаження, що виникають в результаті динамічної взаємодії між елементами машини. Характер навантажень при цих взаємодіях, а отже і характер збуджуваних ними вібрацій визначається конструкцією машини, режимом її роботи, параметрами робочого тіла, технічним станом елементів тощо. Істотним для діагностування є зміна параметрів динамічних навантажень, а отже й порушуваних ними вібрацій при виникненні й розвитку дефекту певного елементу машини. Параметри коливань, що виникають під дією змінюючихся навантажень залежать насамперед від властивостей елементів конструкції, які їх сприймають і, отже, несуть деяку інформацію про ці елементи. Зазначена обставина є основою посередніх методів оцінювання технічного стана машини за показниками збуджуваних у ній коливань, і сьогодні широко використовується в сучасних системах вібродиагностики і моніторингу [1].
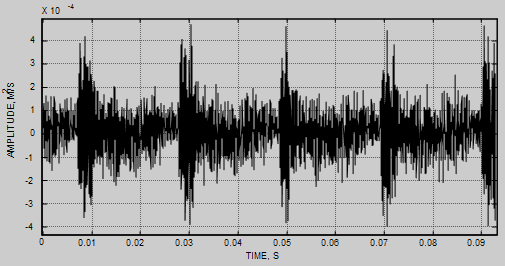
Рисунок 1. - Часова реалізація вибросигналу поршневого компресора за 4 цикли його роботи
Сигнали, що відображають механічні коливання МЗПД мають явно виражений нестаціонарний характер (див. рис. 1). У робочому циклі таких машин часто відбуваються імпульсні процеси (відкриття й закриття клапанів, удари в механічних сполученнях машини та ін.), крім того характер навантажень істотно змінюється в залежності від фази роботи машини (всмоктування, нагнітання) [2].
Переважна більшість існучих систем вібродіагностики використовує оцінки інтегральних показників вібрацій у виділених частотних областях за інтервал часу, що значно перевищує робочий цикл машини, і тому їхні можливості по виявленню дефектів, що зароджуються в окремих сполученнях і вузлах МЗПД, дуже обмежені. Внесок в інтегральні паказникі вібрації МЗПД компонентів, які виникли внаслідок зміни властивостей вузла, що діагностується, може бути занадто малим на фоні результуючої вібрації яка обумовлена коливаннями, що збуджуються, в інших вузлах.
Більш тонкий аналіз вібрацій з урахуванням не тільки розподілу їхньої енергії в частотній області, але і зміни їх у часі, дозволяє встановити більш тісний зв'язок між показниками вібрацій, що оцінюються у такий спосіб, і тими навантаженнями, що їх породжують. Це дозволяє істотно поліпшити можливості диференціальної діагностики машин і підвищити чутливість методу вібродиагностики [3].
Спільний витяг часових і спектральних характеристик сигналів можливе виконувати в рамках теорії частотно-часового аналізу (ЧЧА) [4] і вейвлет аналізу [5]. Для аналізу нестаціонарних сигналів тут використовуються функції двох перемінних, що представляють розподіл енергії сигналу одночасно в часовій і частотній областях, для ЧЧА, або часовій і масштабній областях для вейвлет аналізу. У теорії ЧЧА ці функції звуться частотно-часовими розподілами (ЧЧР), а в теорії вейвлет аналізу скайлограмами (від англ. scale - масштаб). У рамках цих теорій можна виділити декілька найбільш придатних для вирішення задач вібродіагностики методів аналізу нестаціонарних сигналів. До них можна віднести: методи ЧЧА з використанням ядра Цзуя-Уільямса [3, 4], метод вейвлет аналізу з використанням материнських вейвлетів Добеши й Морлета [5].
ЧЧР Цзуя-Уильямса виявляє найбільш вдалим, з точки зору мінімізації інтерференційних компонентів [4]. Цзуй й Уильямс показали, що за допомогою ретельного вибору форми ядра можна мінімізувати інтерференційні компоненти, зберігши при цьому необхідні властивості автономних членів. Це обумовило популярність використання даного розподілу для рішення завдань діагностики машинного встаткування [3]. Основним недоліком ЧЧР Цзуя-Уильямса є його значна надмірність, яка призводить до необхідності реалізації складних алгоритмів обробки великих обсягів даних. Все це визначає необхідність у значних обчислювальних ресурсах і не дозволяє використати даний метод у режимі реального часу. Через те що існує квадратична залежність обсягу ЧЧР від кількості відліків в сегменті сигналу, що обробляється, ускладнюється проведення статистичної обробки ЧЧР (усереднення) сегментів сигналів довжиною більше 2048 відліків, застосування якої могло б значно підвищити вірогідність результатів діагностики. Крім того, неможливо остаточно позбутися інтерференційних компонент, зокрема на краях ЧЧР, внаслідок білінійного характеру перетворення. Деяких недоліків зазначених для ЧЧА позбавлені методи вейвлет аналізу [5].
Метою даної статті є обгрунтування можливості і виробітка рекомендацій щодо використання методів вейвлет аналізу для витягу діагностичної інформації з нестаціонарної вібрації МЗПД.
У рамках даних методів нестаціонарний сигнал аналізується шляхом розкладання його по принципово новому базисі представленому у вигляді сукупності хвильових пакетів, які характеризується чотирма основними принципово важливими властивостями [5]:
- мають вигляд коротких, локалізованих у часі (або в просторі), хвильових пакетів з нульовим значенням інтеграла;
- мають можливість зрушення за часом;
- здатні до масштабування (стиску/розтягання);
- мають обмежений (або локальний) частотний спектр.
Цей базис може бути ортогональним, що помітно полегшує аналіз, дає можливість реконструкції сигналів і дозволяє реалізувати алгоритми швидких вейвлет-перетворень. Однак, є ряд вейвлетів, які властивостями ортогональності не володіють, але які, проте, практично корисні, наприклад, у завданнях аналізу й ідентифікації локальних особливостей віброакустичних сигналів.
Одна з основних ідей вейвлет-перетворення сигналів полягає в розбивці наближення до сигналу на дві складові: грубу (апроксимуючу) і витончену (деталізуючу), з наступним їхнім уточненням ітераційним методом. Кожен крок такого уточнення відповідає певному рівню декомпозиції й реставрації сигналу.
В основі прямого або безперервного вейвлет-перетворення або CWT (Continue Wavelet Transform) лежить використання двох функцій, що є безперервними й інтегруються по всій осі часу [5]:
- вейвлет-функція psi Ψ(t) з нульовим значенням інтеграла (
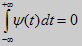 ), яка визначає деталі сигналу й породжує коефіцієнти деталізації;
), яка визначає деталі сигналу й породжує коефіцієнти деталізації; - скейлинг-функція, або функція, яка масштабує phi φ(t) з одиничним значенням інтеграла (
 ). Вона визначає грубе наближення (апроксимацію) сигналу й породжує коефіцієнти апроксимації.
). Вона визначає грубе наближення (апроксимацію) сигналу й породжує коефіцієнти апроксимації.
Phi-функції φ(t) властиві далеко не всім вейвлетам, а тільки тим, які відносяться до ортогональних. Такі вейвлети розглянуті надалі. Psi-функція Ψ(t) створюється на основі тієї або іншої базисної функції Ψ0(t), що, як й Ψ(t), визначає тип вейвлету. Базисна функція повинна задовольняти всім тим вимогам, які були відзначені для psi-функції Ψ(t). Вона повинна забезпечувати виконання двох основних операцій:
- зрушення за часом t- ψ0(t-b) при
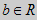 ;
; - масштабування -
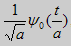 , при a>0 й
, при a>0 й  .
.
Параметр а задає ширину (масштаб) цього вейвлета, a b - його положення. Неважко переконатися в тому, що наступний вираз задає відразу дві ці властивості функції Ψ(t):
(1)
 .
.
Отже, для заданих а і b функція Ψ(t) і є вейвлет. Вейвлеты, позначені як Ψ(t) іноді називають "материнськими вейвлетами", оскільки вони породжують цілий ряд вейвлетів певного роду. Вейвлети є дійснозначними функціями часу. Про вейвлети, які чітко локалізовані у часі говорять, що вони мають компактний носій. Саме такі материнські вейвлети доцільно використовувати для детектування компонент вібросигналів, які породжено ударними навантаженнями (відкриття й закриття клапанів, удари в механічних сполученнях машини та ін.).
Стосовно до сигналів, як функцій часу, параметр 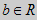 задає положення вейвлету на часовій осі, а параметр а задає його масштабування за часом. Оскільки параметр масштабу а реально може бути тільки позитивним і його не можна брати рівним нулю, то вважається, що а R+-{0}.
задає положення вейвлету на часовій осі, а параметр а задає його масштабування за часом. Оскільки параметр масштабу а реально може бути тільки позитивним і його не можна брати рівним нулю, то вважається, що а R+-{0}.
Пряме безперервне вейвлет-перетворення сигналу s(t) задається по формальній аналогії з перетворенням Фур'є шляхом обчислення вейвлет-коефіцієнтів за формулою [5]:
(2)
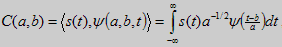 ,
,
де позначення  , означає скалярний добуток відповідних співмножників. З урахуванням обмеженої області визначення сигналів й
, означає скалярний добуток відповідних співмножників. З урахуванням обмеженої області визначення сигналів й 
(3)
 .
.
Отже, вейвлет-коефіцієнти визначаються інтегральним значенням скалярного добутку сигналу на вейвлет-функцію заданого виду. Вираз (3) використовується, як основний для функції прямого безперервного вейвлет-перетворення. Пряме вейвлет-перетворення можна розглядати як розкладання сигналу по всім можливим зрушенням і розтяганням/стискам сигналу s(t). При цьому параметри a й b можуть приймати будь-які значення в межах зазначених вище областей їхнього визначення.
Великі рівні функції C(a,b) характерні тільки для коефіцієнтів тих вейвлетів, які розташовуються поблизу тієї або іншої локальної особливості сигналу, а також у разі якщо характер (форма) цієї локальної особливості сигналу походить на материнський вейвлет. Таким чином, застосування методів вейвлет аналізу для рішення задач віброакустичної діагностики потребує ретельного підбору материнських вейвлетів близьких по формі з відгуками на зміну динамічних навантажень в елементах машини, що діагностуються. Ця задача не є тривіальною і потребує проведення ретельних досліджень динаміки і частотних властивостей кожного типу машин, що діагностуються.
Безперервне пряме вейвлет-перетворення як і ЧЧР має велику надмірність, що веде до невиправдано великих витрат машинного часу на його обчислення. Крім того, скайлограмами залежно від їхньої конкретної реалізації, заданої відповідними програмними засобами, часом можуть давати найрізноманітніше забарвлення тих або інших локальних особливостей сигналу.
В системах вібродіагностики вимоги до швидкості обробки інформації та її об'єму досить часто висуваються на передній план. Наприклад, ці вимоги досить суттєві для портативних систем вібродіагностики. В цьому випадку неможливо використовувати методи аналізу засновані на частотно-часовому аналізу чи безперервному вейвлет перетворенні внаслідок їх складності та надмірності. Для вирішення цієї проблеми доцільно використовувати методи декомпозиції нестаціонарних вібропроцесів засновані на алгоритмі швидкого вейвлет-перетворення (Fast Wavelet Transform). Цей алгоритм також зветься алгоритмом Малла (Mallat algorithm) [5]. Він є ітераційним і реалізує декомпозицію сигналу s(t) засновану на фільтрації, причому кількість ітерацій може бути довільною.
(4)
 .
.
де через а позначені коефіцієнти апроксимації, а через d - деталізуючі коефіцієнти.
Класична схема Малла припускає рекурсивне застосування процедури декомпозиції сигналу в частотній області без явного обчислення a та d. Перший крок алгоритму Малла пояснюється діаграмою вейвлет-декомпозиції сигналу (див. рис. 2).

Рисунок 2. - Діаграма першого кроку алгоритму Малла
Сигнал s(t) подається на фільтри декомпозиції низьких (Lo_D) і високих частот (Hi_D), після чого за допомогою операції децимації ↓2 можна одержати коефіцієнти апроксимації на виході фільтра низьких частот і деталізуючі коефіцієнти на виході фільтра високих частот. Далі цей алгоритм може бути повторено декілька разів (див. рис. 3).
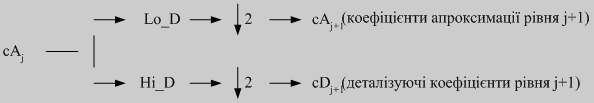
Рисунок 3. - Діаграма вейвлет-розкладу
У результаті декомпозиції формується повний набір апроксимуючих та деталізуючих коефіцієнтів до рівня декомпозиції j+1 (див. рис. 4).
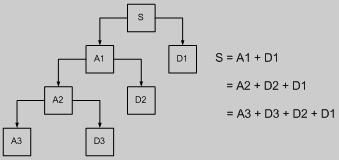
Рисунок 4. - Структура вейвлет-декомпозиції сигналу
По отриманому набору коефіцієнтів будується скайлограма вібропроцесу, що аналізується. Скайлограма має той самий сенс, що і спектрограма, чи частотно-часовий розподіл. Тобто вона представляє розподіл енергії сигналу в області масштаб - час. На рис. 5 наведено приклади скайлограм вібросигналу поршневого компресора отриманих за допомогою материнських вейвлетів Добеши 7 (рис. 5 б) та Морлета (рис. 5 в). Крім того, на рисунку показаний зв'язок скайлограм з часовим представленням вібросигналу. Аналізуючи певні області скайлограми чи окремі деталізуючи або апроксимуючі коефіцієнти можна отримати інформацію про технічний стан машини, що діагностується.
Кількість рівнів декомпозиції і її структура визначається в залежності від частотних характеристик компонент вібросигналу, які містять інформацію про технічний стан певних елементів МЗПД. Припустимо, що для контролю технічного стану різних елементів однієї машини необхідно використовувати різні структури декомпозиції та різні материнськи вейвлети. Тобто для кожного дефекту агрегату можна виділити свої інформативні області "масштаб-час" отримані шляхом розкладання вібросигналу по спеціально підібраному базису.

Рисунок 5. - Зв'язок часового представлення вібросигналу поршневого компресора (а) зі скайлограмами на базі материнських вейвлетів Добеши 7 (б) і Морлета (в), справа наведені відповідні функції ψ(t)
Висновки. Таким чином, у статті викладені основи та обґрунтована доцільність використання методів вейвлет аналізу для віброакустичної діагностики МЗПД. При практичній реалізації цих методів рекомендовано застосовувати алгоритм швидкого вейвлет-перетворення використовуючи материнські вейвлети з компактним носієм.
Показана необхідність у доробці та адаптації запропонованих методів з метою підвищення ефективності й вірогідності діагностики. Для досягнення цієї мети необхідне
- встановлення чітких взаємозв'язків між компонентами скайлограм і технічним станом окремих елементів МЗПД;
- коректний підбір материнських вейвлетів для детектування локальних особливостей віброакустичних сигналів пов'язаних з технічним станом окремих елементів МЗПД;
- розробка алгоритмів прийняття рішень про технічний стан МЗПД, які застосовують у якості вхідних даних масштабно-часові розкладання вібросигналів.
Література
- Явленский К.Н., Явленский А.К. Вибродиагностика и прогнозирование качества механических систем. - Л.: Машиностроение, 1983. - 235 с.
- Воронцов А.Г., Дегтяренко И.В. Математическая модель малого поршневого компрессора// Науковi працi ДонДТУ. Серiя: Обчислювальна технiка та автоматизацiя, випуск 3. - Донецьк: ДонДТУ. -1999. - С. 32-39.
- Дегтяренко И.В. Об использовании частотно-временного анализа виброакустических сигналов при построении систем оценки технического состояния машин возвратно-поступательного действия// Наукові праці ДонДТУ. Серiя: Обчислювальна технiка та автоматизацiя, випуск 12. - Донецьк: ДонДТУ. -1999. - С. 47-53.
- Коэн Л. Время-частотные распределения: Обзор // ТИИЭР. -1989. -Т. 77.- №10. - С. 72-121.
- Дьяконов В.П. Вейвлеты. От теории к практике. - М.: СОЛОН-Р, - 2002. - 448 с.
