СЖАТИЕ ИНФОРМАЦИИ С ПОМОЩЬЮ АЛГОРИТМОВ АДАПТИВНОГО ВЕРОЯТНОСТНОГО КОДИРОВАНИЯ
Лобанов С.В.
Московский государственный авиационный институт (технический университет) 125871. г. Москва, ГСП. Волоколамское шоссе, д. 4, кафедра №402 РСУПИ
Источник http://www.autex.spd.ru/dspa/dspa2002
В настоящее время разработано множество алгоритмов сжатия информации без потерь. Например, только различных модификаций алгоритмов LZ77 и LZ78 насчитывается несколько десятков. Аналогично и для других семейств алгоритмов - хаффмановского и арифметического. Во всех этих семействах алгоритмов, так или иначе, но не всегда в явном виде, используются вероятности появления символов алфавита на текущей позиции последовательности. Следовательно, создание алгоритмов, использующих в явном виде вероятностную структуру информационной последовательности, является важнейшей задачей.
Любой алгоритм сжатия информации можно представить как некоторый преобразователь данных поступающих на его вход. Будем считать, что на входе какого-либо алгоритма сжатия информации имеется последовательность π длиной N символов алфавита X. Примем, что алфавит X состоит из n букв (xi  X, i=1..n). Рассматриваемый алгоритм сжатия информации
преобразовывает эту последовательность символов в некоторую другую, имеющую длину W<N (если рассматривать ее в том же самом алфавите). Последовательность на выходе алгоритма сжатия называется кодом входной последовательности.
X, i=1..n). Рассматриваемый алгоритм сжатия информации
преобразовывает эту последовательность символов в некоторую другую, имеющую длину W<N (если рассматривать ее в том же самом алфавите). Последовательность на выходе алгоритма сжатия называется кодом входной последовательности.
Следует отметить, что не существует алгоритма кодирования информации, который сжимал бы абсолютно любую последовательность данных. Это можно показать простейшими рассуждениями. Допустим, что создан некоторый "суперархиватор", который сжимает любую поданную на его вход последовательность на один символ. Пусть на вход такого "суперархиватора" подаются последовательности длинной N. Очевидно, что всего возможно nN разных входных последовательностей. Так как "суперархиватор" сжимает каждую из входных последовательностей на один символ, т. е. из последовательности длиной N символов создает последовательность длиной N-1 символов, то в этом случае возможно всего nN-1 разных кодовых (выходных) последовательностей. Но тогда очевидно, что некоторые из входных последовательностей, количество которых составляет nN-nN-1, при кодировании неизбежно будут преобразованы в одну и ту же выходную последовательность. Естественно, что при декодировании они правильно восстановлены не будут, т. к. декодер заменит их одной и той же последовательностью. Следовательно, такой "суперархиватор" будет являться алгоритмом сжатия с потерями.
Из рассмотрения работы "суперархиватора" становится ясно, что некоторые из входных последовательностей длины N. общее количество которых составляет nN-nN-1, сжиматься не могут в принципе. Каким бы мощным ни был алгоритм кодирования, длины кодовых последовательностей для этой группы входных последовательностей останется прежней равной N. Можно предположить, что эта группа входных последовательностей относится к так называемым абсолютно случайным последовательностям (АСП). Нетрудно записать формулу для расчета количества абсолютно случайных последовательностей среди всех последовательностей некоторой длины i в алфавите размером N символов:
(1)
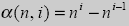
Условимся считать, что α(n,1)=n.
В процессе своей работы идеальный архиватор должен для последовательности длины N, поступившей на его вход, создать АСП, которая будет кодом поступившей последовательности. Для каждой возможной входной последовательности длины N из всей совокупности размером в nN сопоставлена своя собственная кодовая АСП некоторой длины. При этом возможно N различных длин от 1 до N, которые соответствуют N различным коэффициентам сжатия. Очевидно, что тогда общее количество АСП длиной от 1 до N должно быть равно nN, т. е. должно быть справедливо следующее равенство
(2)
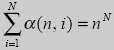
С учетом формулы (1) можно убедиться, что равенство (2) соблюдается.
Таким образом, любую последовательность можно представить в виде двух частей:
- Длины кода для данной входной последовательности;
- Кода последовательности, являющегося АСП определенной длины.
Следовательно, если создать алгоритм определения длины кода любой последовательности и генерации АСП заданной длины, соответствующей заданной последовательности, то получится новый алгоритм сжатия информации оптимальный по своей природе.
Выходную последовательность, т. е. код последовательности, можно рассматривать двояко. Во-первых, его можно рассматривать как некоторое целое число K(π>, удовлетворяющее неравенству
(3)

где M(π) - мощность источника информации, рассчитанная исходя из входной последовательности π. Во-вторых, если разделить все части выражения (3) на величину M(π), то код последовательности можно рассматривать как некоторое действительное число B(π), удовлетворяющее неравенству
(4)

В этом случае код последовательности представляется числом с плавающей точкой меньшим единицы и количество знаков после запятой отождествляет его длину.
По своей сути мощность источника информации, рассчитанная исходя из конкретной входной последовательности, показывает число последовательностей, которые с точки зрения алгоритма сжатия информации идентичны по своей вероятностной структуре данной. Можно показать, что мощность дискретного источника информации необходимо вычислять с помощью следующего выражения
(5)
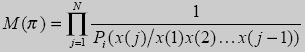
Здесь Pi(x(j)/x(i)x(2)... x(j - 1)) - вероятность появления на j-ой позиции последовательности i-го символа алфавита, оцененная исходя из j-1 предыдущих символов. Очевидно, что чем лучше сжимает алгоритм, тем ближе эти вероятности к единице. Задача алгоритма кодирования заключается в том. чтобы предсказать появление на текущей позиции последовательности определенного символа алфавита и выставить для этого символа максимальное значение вероятности. Для предсказания используются модели источника информации. В настоящее время для этих целей наиболее часто используют методы семейства РРМ[2, 4].
Методы семейства РРМ могут давать нулевую оценку вероятности появления символа алфавита. Как видно из (5) в этом случае невозможно оценить мощность источника информации. Для выхода из этой ситуации можно использовать следующие выражения для оценки вероятности появления символов алфавита на позициях последовательности
(6)

или
(7)

Здесь Pi*(j) - вероятность появления символа алфавита, оцененная в соответствии с каким-либо методом. Заметим, эти выражения удовлетворяют требованию нормировки для суммы вероятностей символов алфавита, т. е.
(8)

В случае, когда выходная последовательность рассматривается как целое число по схеме в соответствии с неравенством (3), то можно получить следующие два способа для расчета кода последовательности:
(9)
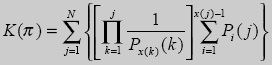
(10)
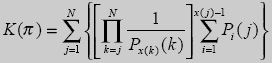
Как было указано выше наряду с (3) к определению кода последовательности возможен и другой принцип. Суть его состоит в том. что код последовательности представляется действительным числом меньшим единицы, как было сделано для неравенства (4). Следовательно, если выражения (9) и (10) разделить на М(π), определяемое выражением (5), то получим следующие соотношения для расчета кода последовательностей, а именно:
(11)
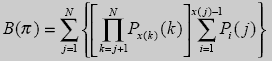
(12)
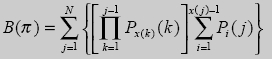
Подставив Pi(j) в формулу (12) из (6) и (7) и проведя дополнительные преобразования. получим
(13)
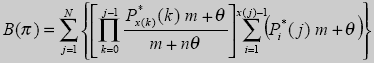
если принять, что Px(0)(0)=(1 - θ)/m , и соответственно
(14)

Bыражения (13) и (14) существенно упрощаются. С помощью такой схемы кодирования и при использовании точной асимптотические свойства алгоритма кодирования. В случае, когда параметр θ = 1 выражения (13) и (14) существенно упрощаются. С помощью такой схемы кодирования и при использовании точной моделирующей схемы, например одного из метода РРМ, можно добиться максимально возможного коэффициента сжатия информации.
Литература
- Амелькин В. А. Методы нумерационного кодирования. - Новосибирск: Наука. 19S6 г. - 15S с.
- Шкарин Д. А. Повышение эффективности алгоритма РРМ. //Проблемы передачи информации. 2001. т. 37. вып. 3, с. 44-54.
- Потапов В. Н. Теория информации. Кодирование дискретных вероятностных источников. Учебное пособие - Новосибирск: Новосиб. гос. унив-тет, 1999 г. - 71 с.
- Bell Т., Witten I. H., Cleary J. G. Modeling for text compression. //ACM Computing Surveys. 19S9, Vol.21. №4, p. 557-591.
