
2.2 Cutting forces
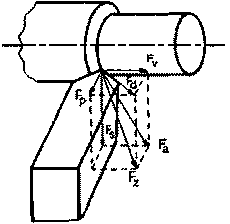
 ) due to Fs force should be ideally zero during cutting.
) due to Fs force should be ideally zero during cutting.
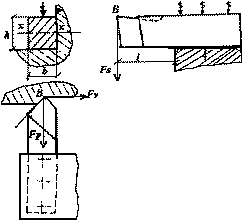
2.3 Castigliano theory
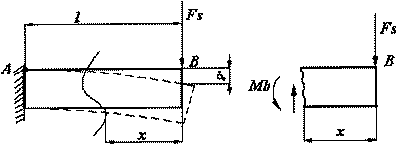
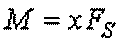

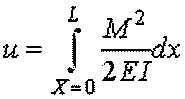
 ) can be found in the following form:
) can be found in the following form:
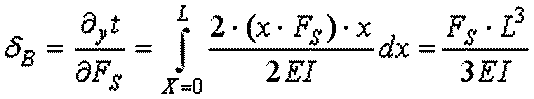
2.4 Finite elements
|
|
| English | Ðóññêèé |


 ) due to Fs force should be ideally zero during cutting.
) due to Fs force should be ideally zero during cutting.


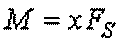

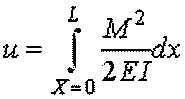
 ) can be found in the following form:
) can be found in the following form:
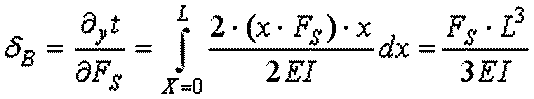
|