К вопросуо силах, действующих на задней поверхности инструмента при резании
А.Б. Кравченко
(http://sstu.edu.ru/research/sstu_works/herald_techsc/10/17.doc)
Вопрос о силах, действующих на задней
поверхности инструмента при резании имеет не только академическое, но и прикладное значение.
Дело в том, что инструменты, как правило, изнашиваются по задним поверхностям, и этот процесс в
основном связан с силовыми взаимодействиями между обрабатываемым изделием и задней поверхностью
инструмента. Определение этих сил сопряжено с известными трудностями.
 Рисунок 1 – Схема сил при свободном резании.
Рисунок 1 – Схема сил при свободном резании.
На рисунке 1 представлена схема сил,
действующих в зоне резания. Силы PN и FN на передней
поверхности и соответственно N и F3 на задней являются следствием
внедрения резца под действием равнодействующей силы R. В силу вневершинного расположения
силы возникает момент M.
На основании рис. 1. можно записать уравнения механики резания:
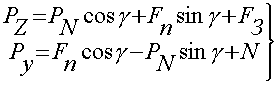 ; (1)
Два уравнения (1) имеют четыре неизвестные
величины. Силы PZ и PY определяются динамометрированием.
Методику определения сил F3 и N предложил проф. А.И. Розенберг [1].
Суть методики заключается в следующем. Производят резание с уменьшающейся толщиной среза
a в условиях постоянной температуры, величина которой поддерживается соответствующим
подбором скорости резания. При этом замеряются силы резания PZ и P
Y . Результаты наносятся в координатной системе PZ(P
Y) – a. В этих условиях зависимости PZ = f(a) и
PY = f(a) имеют вид прямых линий. Отрезки, которые отсекаются на оси
PZ(PY) с учетом масштаба, считаются искомыми силами N
и F3 (рисунок 2). Этот метод в литературе называется «метод экстраполяции на
нулевую толщину среза». В основе описанного метода лежат допущения, что толщина среза не влияет
на силы, возникающие на задней поверхности инструмента, и силы на передней и задней поверхностях
являются отдельными группами и не связаны между собой.
; (1)
Два уравнения (1) имеют четыре неизвестные
величины. Силы PZ и PY определяются динамометрированием.
Методику определения сил F3 и N предложил проф. А.И. Розенберг [1].
Суть методики заключается в следующем. Производят резание с уменьшающейся толщиной среза
a в условиях постоянной температуры, величина которой поддерживается соответствующим
подбором скорости резания. При этом замеряются силы резания PZ и P
Y . Результаты наносятся в координатной системе PZ(P
Y) – a. В этих условиях зависимости PZ = f(a) и
PY = f(a) имеют вид прямых линий. Отрезки, которые отсекаются на оси
PZ(PY) с учетом масштаба, считаются искомыми силами N
и F3 (рисунок 2). Этот метод в литературе называется «метод экстраполяции на
нулевую толщину среза». В основе описанного метода лежат допущения, что толщина среза не влияет
на силы, возникающие на задней поверхности инструмента, и силы на передней и задней поверхностях
являются отдельными группами и не связаны между собой.
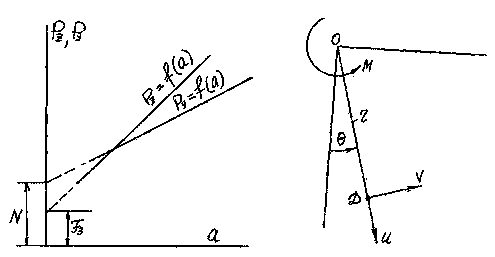 Рисунок 2 – Экстраполяция сил на нулевую толщину среза.
Рисунок 2 – Экстраполяция сил на нулевую толщину среза.
Силы, найденные с использованием указанной
методики отличаются крайне небольшими значениями, на уровне 1,5–3 кг на погонный миллиметр
режущей кромки. Возникает законный вопрос: за счет чего происходит износ инструментов, имеющих
высокую твердость? Более того, известно, что с увеличением толщины среза износ интенсифицируется.
Еще большее недоумение вызывает тезис о независимости сил на передней и задней поверхностях
инструмента. Этот вопрос нами рассматривается ниже.
Пусть в точке O полубесконечной пластины
приложен момент M (рисунок 2).
Положительное направление полярного угла θ принято в направлении против часовой
стрелки. На этом же рисунке показаны положительные направления перемещений U и V.
Напряжения, которые возникают в пластине от действия момента, описываются зависимостями [2], [3]:
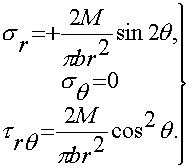 ; (2)
Деформации определим на основании закона Гука:
; (2)
Деформации определим на основании закона Гука:
 ; (3)
где
; (3)
где 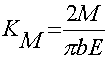 ; b – ширина пластины;
m – коэффициент Пуассона; E – модуль упругости.
; b – ширина пластины;
m – коэффициент Пуассона; E – модуль упругости.
Выражая деформации через перемещения, получим дифференциальные соотношения:
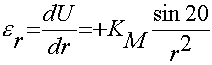 ; (4)
; (4)
 ; (5)
; (5)
 ; (6)
Перемещая и интегрируя выражение (4), найдем:
; (6)
Перемещая и интегрируя выражение (4), найдем:
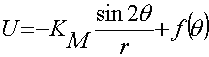 ; (7)
где f = (θ) является функцией одного только θ.
Подставляя (7) в (5) и интегрируя, получим выражение для определения V:
; (7)
где f = (θ) является функцией одного только θ.
Подставляя (7) в (5) и интегрируя, получим выражение для определения V:
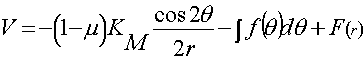 ; (8)
где f = (r) является функцией одного только r.
Далее, если (7) и (8) подставить в зависимость (6), то после преобразований найдем равенство:
; (8)
где f = (r) является функцией одного только r.
Далее, если (7) и (8) подставить в зависимость (6), то после преобразований найдем равенство:
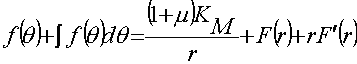 ; (9)
Это равенство должно удовлетворяться при любых значениях r и θ, поэтому каждая
из двух независимых частей этого равенства должна быть равна нулю.
; (9)
Это равенство должно удовлетворяться при любых значениях r и θ, поэтому каждая
из двух независимых частей этого равенства должна быть равна нулю.
Рассмотрим левую часть равенства (9):
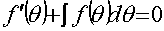 ; (10)
Решение уравнения (10) имеет вид:
; (10)
Решение уравнения (10) имеет вид:
 ; (11)
Аналогично для правой части равенства (9):
; (11)
Аналогично для правой части равенства (9):
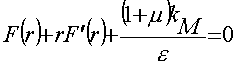 и соответственно:
и соответственно:
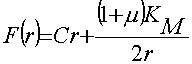 ; (12)
; (12)
Подставляя (11) в (7) и (11), (12) в (8) будем иметь:
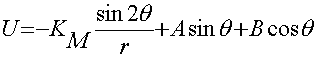 ; (13)
; (13)
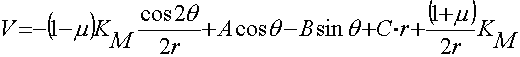 ; (14)
; (14)
Исключая перемещения пластины как твердого тела,следует положить A = B = C = 0.
Таким образом, зависимости для перемещений приводятся к виду:
 ; (15)
; (15)
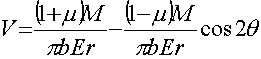 ; (16)
; (16)
В конечном итоге нас интересуют перемещения части
материала в левой и правой частях пластины (y<0 и y>0).
Очевидно, что при:
θ = 0, U =0,
 ; (17)
; (17)
θ = ±p/2, U =0,
 ; (18)
Перемещения, которые вытекают из
зависимостей (17) и (18), графически могут быть интерпретированы как это показано на рисунок 4, а, б.
Если обратиться к рассмотрению рисунок 1 с учетом формул (17), (18) и построения на рисунок 4,б, можно
утверждать, что под задней поверхностью резца за счет сил, действующих на передней поверхности (момент М),
обработанная поверхность детали будет стремиться к «выпучиванию» (см. рис.4,б), т.е. возникает упругое
взаимодействие между этой поверхностью и площадкой износа резца по задней поверхности. С увеличением
параметров процесса резания растет момент резания, что сопровождается повышением напряженного состояния
в районе задней поверхности инструмента. Более того, силы, возникающие в районе площадки износа резца,
могут достичь значительных величин. Последнее подтверждается прямыми исследованиями с помощью метода
разрезного резца [4], а также и подсчетами, приведенными в работе [5]. В работе [5] установлено, что,
например, при резании стали ШХ15 в состоянии поставки резцом Т15К6, g
= 0, a = 10; v = 100 м/мин при толщине среза a =0,25 мм
(резание свободное) и износе резца w = 0,05 мм, сила N достигает значения P = 200 H на погонный
миллиметр режущей кромки, что приводит к возникновению напряжений, равных s
N = 400 МПа. Уместно заметить, что резание с толщиной a = 0,5 мм дает
соответственно P = 300 Н и N = 600 МПа. Такой уровень напряжений достаточен
для интенсификации износа.
; (18)
Перемещения, которые вытекают из
зависимостей (17) и (18), графически могут быть интерпретированы как это показано на рисунок 4, а, б.
Если обратиться к рассмотрению рисунок 1 с учетом формул (17), (18) и построения на рисунок 4,б, можно
утверждать, что под задней поверхностью резца за счет сил, действующих на передней поверхности (момент М),
обработанная поверхность детали будет стремиться к «выпучиванию» (см. рис.4,б), т.е. возникает упругое
взаимодействие между этой поверхностью и площадкой износа резца по задней поверхности. С увеличением
параметров процесса резания растет момент резания, что сопровождается повышением напряженного состояния
в районе задней поверхности инструмента. Более того, силы, возникающие в районе площадки износа резца,
могут достичь значительных величин. Последнее подтверждается прямыми исследованиями с помощью метода
разрезного резца [4], а также и подсчетами, приведенными в работе [5]. В работе [5] установлено, что,
например, при резании стали ШХ15 в состоянии поставки резцом Т15К6, g
= 0, a = 10; v = 100 м/мин при толщине среза a =0,25 мм
(резание свободное) и износе резца w = 0,05 мм, сила N достигает значения P = 200 H на погонный
миллиметр режущей кромки, что приводит к возникновению напряжений, равных s
N = 400 МПа. Уместно заметить, что резание с толщиной a = 0,5 мм дает
соответственно P = 300 Н и N = 600 МПа. Такой уровень напряжений достаточен
для интенсификации износа.
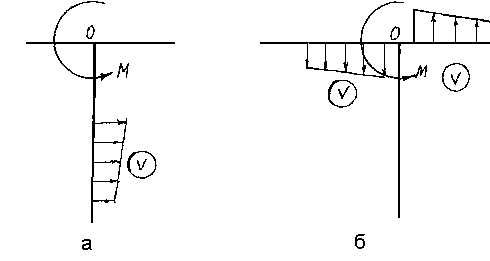 Рисунок 2 – Интерпретированы графически.
Рисунок 2 – Интерпретированы графически.
Таким образом, путем решения упругой задачи
получены зависимости, на базе которых можно сделать заключение, что силы, возникающие на задней
поверхности инструмента при резании, функционально связаны с напряженным состоянием на передней
поверхности и зависят от режимов обработки.
Перечень ссылок
- Розенберг А.М., Еремин А.Н. Элементы теории процессов резания металлов. М.: Машгаз, 1956, 320 с.
- Фрохт М.М. Фотоупругость. Том 2. Из-во Техн.-теорет. лит.. М., 1950. 488 с.
- Тимошенко С.П., Гудьер Дж. Теория упругости. М.: Наука, 1975. 575 с.
- Гордон М.Б.. Трение, смазка и износ инструмента при резании металлов. Чебоксары, 1978. 125 с.
- Кравченко А.Б. Обоснование заданных эксплуатационных характеристик деталей ГТД путем целенаправленного регулирования остаточных напряжений при лезвийной обработке: Дис. канд. техн. наук. Куйбышев, 1990.

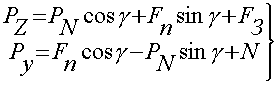 ; (1)
; (1)
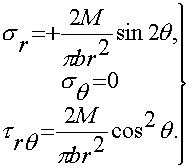 ; (2)
; (2) ; (3)
; (3)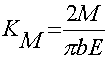 ; b – ширина пластины;
m – коэффициент Пуассона; E – модуль упругости.
; b – ширина пластины;
m – коэффициент Пуассона; E – модуль упругости.
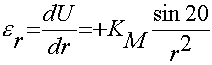 ; (4)
; (4) ; (5)
; (5) ; (6)
; (6)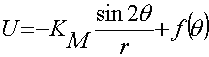 ; (7)
; (7)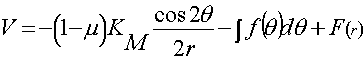 ; (8)
; (8)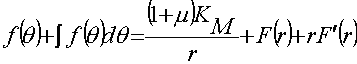 ; (9)
; (9)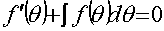 ; (10)
; (10) ; (11)
; (11)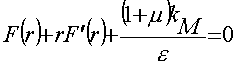
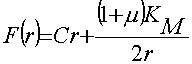 ; (12)
; (12)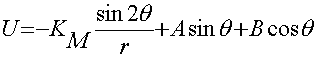 ; (13)
; (13)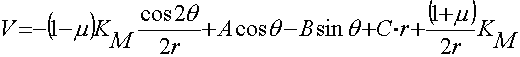 ; (14)
; (14) ; (15)
; (15)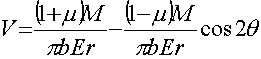 ; (16)
; (16) ; (17)
; (17) ; (18)
; (18)