|Автобиография
|Автореферат работы
|Библиотека
|Ссылки
|Отчет о поиске
|Индивидуальное задание|
|Страница ДонНТУ| Портал магистров|
ОБЕСПЕЧЕНИЕ КАЧЕСТВА ОБРАБОТКИ ШЛИФОВАНИЕМ НА ОСНОВЕ СИНТЕЗА ОПТИМАЛЬНЫХ ДИНАМИЧЕСКИХ СВОЙСТВ СТАНКА
Б. М. Бржозовский, М. Б. Бровкова, И. Н. Янкин
Саратовский государственный технический университет
http://www.vstu.ru/research/pub/izvestiya/2006_2/07.pdf
Получение качественных поверхностей изделий при абразивной обработке связано как правило с обеспечением оптимального сочетания технологических факторов с динамическим состоянием станка. Проявляющаяся зачастую нестабильность резания приводит к ухудшению показателей обработки вследствие возбуждения в зоне резания чрезмерного уровня колебаний.
С целью уменьшения вероятности образования детерминированной вибрации на частотах собственных и вынужденных форм колебаний обычно используют ограничение режимов резания. Отсюда следует простой вывод о возможности повышения качества обработки путем улучшения динамического состояния станка. Однако стремление проектировать наиболее ответственные узлы с улучшенными динамичеcкими характеристиками не всегда приводят к желаемому результату. Это связано со способностью формообразующих подсистем станка образовывать при резании отличные от ожидаемых динамические свойства. В статье рассматривается один из подходов к обеспечению качества обработки внутренним шлифованием на основе синтеза оптимальных динамических свойств формообразующих подсистем с учетом их нелинейного взаимодействия через зону резания.
Известно, что колебательный процесс в классическом понимании является отражением реакции динамической системы на ее возмущение. Важной систематической составляющей колебательных движений, как показали исследования, являются собственные формы колебаний. Параметры собственных форм колебаний определяются упругими, инерционными, диссипативными характеристиками элементов механической системы станка, процесса резания и связей между ними. Промежуточным звеном, позволяющим увязать параметры колебательного процесса и характеристики механической системы, являются динамические свойства станка – склонность к образованию устойчивых движений в виде определенных форм колебаний, нечувствительность к возмущению колебаний в определенном диапазоне частот, наличие резонансных и антирезонансных областей динамического взаимодействия подсистем и другие.
С целью раскрытия механизма взаимодействия формообразующих подсистем обратимся к модели движений инструмента и изделия при шлифовании. Она построена на основе учета особенности процесса шлифования, заключающейся в наличии высокого удельного веса работы трения в общей работе шлифования, и имеет вид:

где i m , эi c , эi p – эквивалентные параметры подсистем инструмента (i=1,2) и изделия (i=3,4); c ,p – коэффициенты, отражающие характеристики контактного взаимодействия абразивного круга с изделием; i µ – коэффициенты нелинейной связи возбуждающих сил с изменением скорости относительного скольжения инструмента с изделием и их сближением.
В обобщенном виде каждая из подсистем инструмента и изделия описывается двумя парами парциальных систем:
нормальной системой абразивного инструмента, имеющей вследствие наличия консольной оправки изгибной характер (координата x1 );
тангенциальной системой абразивного инструмента, имеющей изгибно-крутильный характер (координата x2 );
нормальной изгибной системой изделия (координата x 3 );
тангенциальной изгибно-крутильной системой изделия (координата x 4 ).
Между подсистемами действуют направленные связи, формируемые процессом резания. Они реализуются в виде подъемной силы ![]() , имеющей скоростную связь с относительным движением инструмента и изделия,и тангенциальной силы
, имеющей скоростную связь с относительным движением инструмента и изделия,и тангенциальной силы ![]() , имеющей упругую связь по нормальному сближению поверхностей инструмента и изделия.
, имеющей упругую связь по нормальному сближению поверхностей инструмента и изделия.
Применение известных асимптотических методов [1] к системе (1) позволяет описать механизм формирования движений в подсистемах и оценить их устойчивость. Взаимодействие подсистем инструмента и изделия как классической автоколебательной системы можно представить в виде схемы, изображенной на рис. 1.
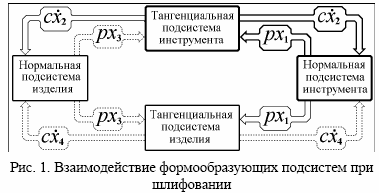
Опираясь на результаты исследований, раскроем подробнее механизм взаимодействия подсистем в условиях их возбуждения процессом резания в русле влияния на динамику и качество обработки.
В обычных условиях формообразующая подсистема инструмента обладает повышенной склонностью к возбуждению колебаний (является доминирующей), что приводит к образованию колебательных движений в виде изгиба оправки с кругом. Указанная форма колебаний является неблагоприятной, поскольку оказывает существенное отрицательное влияние на процесс формирования микрогеометрических параметров обрабатываемой поверхности.
Рассмотрим влияние взаимодействия подсистем на устойчивость движений на частоте изгиба оправки с кругом. В качестве меры возбуждения подсистем используем величину произведения коэффициентов возбуждающих сил ( cp) , которая отражает интенсивность взаимодействия контактирующих поверхностей инструмента и изделия. В зависимости от величины возбуждения динамическая система шлифования может находиться в следующих состояниях.
Случай c =0 , p = 0. Указанное состояние динамической системы соответствует отсутствию контакта инструмента с изделием, например, на этапе подвода инструмента в зону обработки. В этом случае система (1) принимает вид совокупности несвязанных диссипативных осцилляторов, и состояние равновесия динамической системы в начале координат обладает асимптотической устойчивостью в целом.
Случай (cp) > 0соответствует процессу обработки. Здесь можно выделить частный случай, когда работа возбуждающих сил, вносящих энергию в систему, уравновешивается работой диссипативных сил, рассеивающих ее.
Обозначим указанный уровень возбуждения (ср)*. В зависимости от действующего уровня возбуждения по отношению к величине ( cp)* динамическая система может находиться в следующих состояниях.
Область состояний (cp )< (cp )* . Возмущенные малые колебания в системе с течением времени затухают и стремятся к единственному устойчивому состоянию – положению равновесия в начале координат с нулевыми амплитудами. Указанное состояние динамической системы характеризуется доминированием диссипативного фактора над возбуждающим, и произвольные возмущения приводят к затуханию движений. Состояние движений системы может быть описано сходящимися к началу координат фазовыми траекториями. Динамическую систему можно охарактеризовать как асимптотически устойчивую в целом, поскольку фазовые траектории сходятся к устойчивому фокусу с центром в положении покоя системы.
Область состояний (cp ) >( cp)* . При произвольных начальных условиях, отличных от нуля, движения в динамической системе стремятся к нарастанию. Данный случай соответствует доминированию возбуждающего фактора над диссипативным. В условиях, когда приток энергии в систему превышает граничный уровень ( cp)* , в динамической системе происходит развитие колебаний, и она движется к новому балансному состоянию – предельному циклу.
Таким образом, динамическая система шлифования может находиться в двух различных состояниях. Следует отметить, что в обоих состояниях движение связанных подсистем инструмента и изделия подчиняется закону, определяемому действием в области резания направленных связей. Причем, в послеграничной области динамическая система шлифования может быть квалифицирована как детерминированная автоколебательная система. Вместе с тем, если учесть, что возбуждающий фактор при шлифовании, оцениваемый величиной cp , формируется за счет множества случайных контактов – фрагментов ПС круга с обрабатываемым материалом, то динамическую систему в дограничной области можно квалифицировать как стохастическую автоколебательную систему. Движение системы в этом случаеможно рассматривать как непрерывный переходной процесс между состояниями, ограниченными положением покоя системы и предельными автоколебательными циклами.
Граница, разделяющая указанные состояния, может быть описана выражениями вида ![]() , устанавливающими зависимость граничного значения возбуждающего фактора с соотношением параметров формообразующих подсистем на автоколебательных частотах ωj .
, устанавливающими зависимость граничного значения возбуждающего фактора с соотношением параметров формообразующих подсистем на автоколебательных частотах ωj .
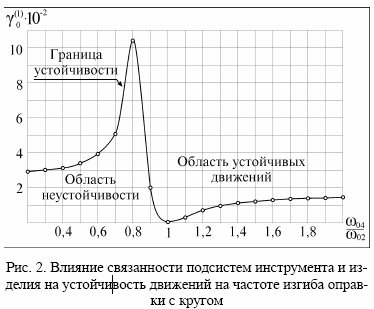
Исследования показали, что по критерию связанности можно выделить две области устойчивости движений на частоте изгиба оправки с кругом (рис. 2). Кривая на рисунке представляет собой геометрическое место точек, соответствующих значениям границы устойчивости движений. Область значений показателя устойчивости ![]() , расположенная выше кривой, соответствует устойчивому автоколебательному режиму. Сочетания параметров динамической
системы, находящихся ниже кривой, отражают неустойчивые стохастические автоколебательные режимы.
, расположенная выше кривой, соответствует устойчивому автоколебательному режиму. Сочетания параметров динамической
системы, находящихся ниже кривой, отражают неустойчивые стохастические автоколебательные режимы.
Раздел двух областей располагается при отношении частот ![]() где ω 04 – парциальная частота тангенциальной подсистемы изделия, а 01 ω – парциальная частота нормальной подсистемы инструмента. Указанное значение отношения частот соответствует максимальной склонности системы к возбуждению детерминированной вибрации на частоте изгиба инструмента. Точка с отношением частот
где ω 04 – парциальная частота тангенциальной подсистемы изделия, а 01 ω – парциальная частота нормальной подсистемы инструмента. Указанное значение отношения частот соответствует максимальной склонности системы к возбуждению детерминированной вибрации на частоте изгиба инструмента. Точка с отношением частот ![]() определяет
наиболее неустойчивое состояние динамической системы с высокой вероятностью возбуждения автоколебаний инструмента на частоте изгиба. Отсюда следует, что с позиций обеспечения качества обработки целесообразно ограничить связанность подсистем областью отношений частот
определяет
наиболее неустойчивое состояние динамической системы с высокой вероятностью возбуждения автоколебаний инструмента на частоте изгиба. Отсюда следует, что с позиций обеспечения качества обработки целесообразно ограничить связанность подсистем областью отношений частот ![]() которая соответствует наибольшему демпфированию колебаний на частоте изгиба оправки с кругом.
которая соответствует наибольшему демпфированию колебаний на частоте изгиба оправки с кругом.
На основе установленного механизма взаимодействия подсистем инструмента и изделия при резании сформирована стратегия коррекции динамических свойств системы шлифования по критерию качества обработки [2]. Изменение параметров формообразующих подсистем в сторону обеспечения оптимальных динамических свойств станка в зоне резания осуществляется в виде динамической настройки. Ее целью является синтез таких динамических свойств станка в зоне резания, которые обеспечивают минимизацию склонности системы к образованию детерминированной вибрации на частотах неблагоприятных форм колебаний.
Изложенные принципы синтеза оптимальных свойств динамической системы шлифования путем исследования взаимосвязи качественных показателей процесса обработки, сопровождающего колебательного процесса и динамических свойств станка с учетом нелинейных связей в зоне резания легли в основу разработки ряда устройств коррекции динамических характеристик станка, показавших хорошие результаты по обеспечению качества обработки.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Моисеев, Н. Н. Асимптотические методы нелинейной механики/ Н. Н. Моисеев. – 2 изд., перераб. – М.: Наука, 1981. – 400 с.
2. Бржозовский, Б. М. Схема создания оптимальной динамической среды в зоне обработки с целью повышения качества шлифованных поверхностей/ Б. М. Бржозовский, И. Н. Янкин// Прогрессивные направления развития технологии машиностроения: межвуз. сб. научн. тр. – Саратов: СГТУ, 2002. – С. 131–135.

