УДК 621.313.33:519.876.5
ВДОСКОНАЛЕННЯ АЛГОРИТМУ ФУНКЦІОНУВАННЯ ЦИФРОВОГО ЗАДАТЧИКА ПОЛОЖЕННЯ ДЛЯ СИСТЕМ ПОЗИЦІЙНОГО ЕЛЕКТРОПРИВОДУ, ОПТИМАЛЬНИХ ЗА ТЕПЛОВИМИ ВТРАТАМИ
Бабенко А.В., студент; Розкаряка П.І, аспирант; Толочко О.І., проф., д.т.н.
(Донецький національний технічний університет, м. Донецьк, Україна)
Одним із засобів зниження непродуктивних втрат електроенергії при керуванні позиційними механізмами є застосування задавальних пристроїв (ЗП), які формують бажані діаграми зміни положення та його похідних під час пересування робочого орга-ну виконавчого механізму.
Якщо бажані діаграми розраховані з умов забезпечення мінімуму теплових втрат, то вони можуть бути успішно реалізовані тільки у цифровій формі.
Зазвичай такі ЗП спочатку формують діаграму завдання на прискорення 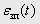 у вигляді кусочно-лінійної апроксимації табличної залежності, вузлові точки якої розраховуються, виходячи з величини бажаного переміщення
у вигляді кусочно-лінійної апроксимації табличної залежності, вузлові точки якої розраховуються, виходячи з величини бажаного переміщення 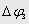 та бажаного часу його відпрацьовування
та бажаного часу його відпрацьовування 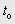 з урахуванням обмежень на швидкість
з урахуванням обмежень на швидкість 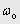 та прискорення
та прискорення 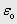 приводу у відповідності з прийнятим критерієм оптимізації. Отриманий у такий спосіб сигнал двічі інтегрується для формування бажаних діаграм зміни швидкості
приводу у відповідності з прийнятим критерієм оптимізації. Отриманий у такий спосіб сигнал двічі інтегрується для формування бажаних діаграм зміни швидкості 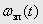 і положення
і положення 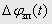 .
.
Координати точок зламу графіка 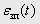 спочатку розраховують у неперервному часі. Потім абсциси вузлових точок коригуються у такий спосіб, щоб вони стали кратними періоду дискретності
спочатку розраховують у неперервному часі. Потім абсциси вузлових точок коригуються у такий спосіб, щоб вони стали кратними періоду дискретності 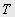 , а ординати цих точок – у такий спосіб, щоб внаслідок коректування абсцис не змінилась величина завданого переміщення та загальний вигляд діаграм. Формули та методика корекції наведені в роботі [1]. Тому далі будемо розглядати діаграми, у яких абсциси всіх характерних точок кривої завдання на прискорення уже кратні періоду переривання.
, а ординати цих точок – у такий спосіб, щоб внаслідок коректування абсцис не змінилась величина завданого переміщення та загальний вигляд діаграм. Формули та методика корекції наведені в роботі [1]. Тому далі будемо розглядати діаграми, у яких абсциси всіх характерних точок кривої завдання на прискорення уже кратні періоду переривання.
В [2, 3] показано, що за умов екстраполяції сигналу завдання на прискорення екстраполятором нульового порядку, вихідний графік треба зсунути на половину періоду переривання вправо. Це дозволяє запобігти накопичення похибки в сигналі завдання на переміщення, але не усуває усталеної похибки в цьому сигналі.
Метою даної роботи є пояснення причин цього явища та визначення величини похибки.
При чисельному інтегруванні (ЧІ) найчастіше застосовують цифрові інтегратори з передаточними функціями (ПФ)
Саме такі методи ЧІ можна встановлювати у блоці Discrete-Time Integrator програми структурного моделювання Simulink пакета MATLAB, який, завдяки наявності в ньому додатку Real Time Workshop, може розглядатися як один із можливих варіантів програмної реалізації цифрових пристроїв систем керування електроприводами постійного струму [4].
Результати моделювання показали, що для забезпечення збіжності дискретної екстрапольованої тахограми 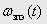 та еталонної аналогової тахограми
та еталонної аналогової тахограми 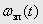 у миті часу, кратні періоду переривання, перший інтегратор повинен мати ПФ (2). У якості другого інтегратора зазвичай пропонують інтегратор з ПФ (3), здійснюючий ЧІ методом трапецій.
у миті часу, кратні періоду переривання, перший інтегратор повинен мати ПФ (2). У якості другого інтегратора зазвичай пропонують інтегратор з ПФ (3), здійснюючий ЧІ методом трапецій.
Знайдемо аналітичний вираз для усталеного сигналу завдання на положення.
Аналоговий сигнал завдання на швидкість змінюється за законом:
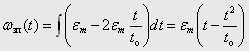 . . |
(4) |
Точне значення переміщення, яке відпрацьовується зі швидкістю, зміна якої задана виразом (5), визначається формулою:
 , , |
(5) |
а приблизне значення, розраховане методом трапецій з кроком 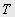 , при парній кількості періодів дискретності на інтервалі
, при парній кількості періодів дискретності на інтервалі 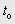 (
( 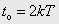 ,
, 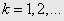 ) – формулою
) – формулою
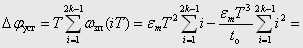
 .
.
Після підстановки 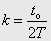 та перетворень маємо
та перетворень маємо
 . . |
(6) |
Усталена похибка сигналу завдання на положення, зумовлена неточністю чисельного інтегрування визначає різністю між значеннями сигналів (5) і (6):
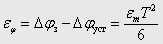 . . |
(7) |
Для усунення усталеної похибки в сигналі завдання на положення слід розглянути можливість використання ЦІ, який здійснює інтегрування методом Сімпсона. На це будуть спрямовані подальші дослідження розглянутої проблеми.
Перелік посилань
- Розкаряка П.И. Коррекция оптимальных по тепловым потерям диаграмм отработки перемещений с учетом эффекта квантования по времени // Наукові праці ДонНТУ. Серія «Електротехніка і енергетика». – Донецьк: ДонНТУ. – 2006. –№112. –С. 71-75.
- Толочко О.И., Коцегуб П.Х., Розкаряка П.И. Особенности цифровой реализации оптимальных алгоритмов управления позиционным электроприводом // Вісник Кременчуцького державного політехнічного університету: Наукові праці КДПУ. – Кременчук: КДПУ. – 2006. – №3 (38). – Ч.1. – С. 8-11.
- Полинский С.В., Розкаряка П. И., Толочко О.И. Повышение точности численного интегрирования при формировании диаграмм перемещения, оптимальных по тепловым потерям. – Вісник кафедри «Електротехніка» за підсумками наукової діяльності студентів. – Донецьк: ДонНТУ. – 2006. – С. 99-100.
- Коцегуб П.Х., Толочко О.И., Федоряк Р.В. Практическая реализация цифровых САУ в среде пакета МАТЛАБ с использованием платформы реального времени «QNX TARGET» // Вісник Національного Технічного Університету «Харківський політехнічний інститут». Збірка наукових праць «Проблеми автоматизованого електропри-воду. Теорія i практика».– Харків: НТУ «ХПI», 2002, №12. – Т.1. – С. 98-101.
Первоисточник: Вісник кафедри «Електротехніка» за підсумками наукової діяльності студентів. – Донецьк, ДонНТУ, 2007 – С. 7-8
Всеукраїнська науково-технічна конференція студентів «Електротехніка, електроніка та мікропроцесорна техніка» 30-31 травня 2007 р. - Донецьк, ДонНТУ
















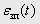 у вигляді кусочно-лінійної апроксимації табличної залежності, вузлові точки якої розраховуються, виходячи з величини бажаного переміщення
у вигляді кусочно-лінійної апроксимації табличної залежності, вузлові точки якої розраховуються, виходячи з величини бажаного переміщення 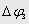 та бажаного часу його відпрацьовування
та бажаного часу його відпрацьовування 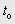 з урахуванням обмежень на швидкість
з урахуванням обмежень на швидкість 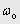 та прискорення
та прискорення 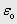 приводу у відповідності з прийнятим критерієм оптимізації. Отриманий у такий спосіб сигнал двічі інтегрується для формування бажаних діаграм зміни швидкості
приводу у відповідності з прийнятим критерієм оптимізації. Отриманий у такий спосіб сигнал двічі інтегрується для формування бажаних діаграм зміни швидкості 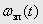 і положення
і положення 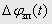 .
. 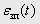 спочатку розраховують у неперервному часі. Потім абсциси вузлових точок коригуються у такий спосіб, щоб вони стали кратними періоду дискретності
спочатку розраховують у неперервному часі. Потім абсциси вузлових точок коригуються у такий спосіб, щоб вони стали кратними періоду дискретності 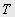 , а ординати цих точок – у такий спосіб, щоб внаслідок коректування абсцис не змінилась величина завданого переміщення та загальний вигляд діаграм. Формули та методика корекції наведені в роботі [1]. Тому далі будемо розглядати діаграми, у яких абсциси всіх характерних точок кривої завдання на прискорення уже кратні періоду переривання.
, а ординати цих точок – у такий спосіб, щоб внаслідок коректування абсцис не змінилась величина завданого переміщення та загальний вигляд діаграм. Формули та методика корекції наведені в роботі [1]. Тому далі будемо розглядати діаграми, у яких абсциси всіх характерних точок кривої завдання на прискорення уже кратні періоду переривання. ,
,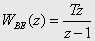 ,
, .
.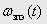 та еталонної аналогової тахограми
та еталонної аналогової тахограми 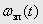 у миті часу, кратні періоду переривання, перший інтегратор повинен мати ПФ (2). У якості другого інтегратора зазвичай пропонують інтегратор з ПФ (3), здійснюючий ЧІ методом трапецій.
у миті часу, кратні періоду переривання, перший інтегратор повинен мати ПФ (2). У якості другого інтегратора зазвичай пропонують інтегратор з ПФ (3), здійснюючий ЧІ методом трапецій.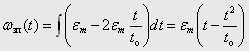 .
. ,
,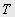 , при парній кількості періодів дискретності на інтервалі
, при парній кількості періодів дискретності на інтервалі 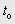 (
( 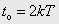 ,
, 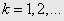 ) – формулою
) – формулою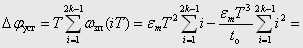
 .
.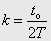 та перетворень маємо
та перетворень маємо .
.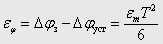 .
.






