УДК 62-83
ПАРАМЕТРИЧЕСКИЙ СИНТЕЗ СИСТЕМЫ ПОДЧИНЕННОГО РЕГУЛИРОВАНИЯ ПОЛОЖЕНИЯ
Бабенко А.В., магистрант; Розкаряка П.И., ассистент; Толочко О.И., проф., д.т.н.
(Донецький національний технічний університет, м. Донецьк, Україна)
При параметрическом синтезе систем подчиненного регулирования обычно используют упрощенные условия модульного оптимума, порождающие метод двойных пропорций, когда постоянная времени интегрирования каждого следующего контура оказывается вдвое больше постоянной времени интегрирования предыдущего контура. Такая настройка обеспечивает небольшое перерегулирование в переходных функциях каждого контура (5-8 %). В частности для системы регулирования положения (СРП) электропривода постоянного тока с подчиненными контурами скорости и тока якоря, передаточная функция замкнутого контура регулирования положения (КРП) при пренебрежении влиянием внутренней обратной связи по ЭДС двигателя имеют вид:
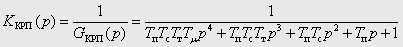 , , |
(1) |
где  – постоянные времени интегрирования разомкнутых контуров положения, скорости и тока соответственно;
– постоянные времени интегрирования разомкнутых контуров положения, скорости и тока соответственно; 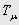 – малая некомпенсируемая постоянная времени привода.
– малая некомпенсируемая постоянная времени привода.
Переходная функция КРП при
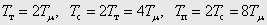 |
(2) |
изображена на рис. 1 (кривая 1).
Особенностью систем регулирования положения, работающих в режиме позиционирования, является то, что для них иногда даже такая малая величина перерегулирования является недопустимой. Уменьшить перерегулирование в переходной функции контура положения без изменения настройки внутренних контуров (скорости и тока) можно увеличением постоянной времени интегрирования внешнего контура, что приводит к снижению его быстродействия. Для демонстрации этого факта на рис. 1 приведена переходная функция КРП при
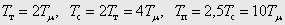 |
(3) |
Целью данной работы является разработка методики синтеза системы регулирования положения, обеспечивающей снижение перерегулирования ее переходной функции без уменьшения быстродействия.
Для достижения этой цели воспользуемся инструментами оптимизации, входяшими в состав пакета MATLAB, в частности функцией
P = lsqnonlin (f, P0)
которая осуществляет поиск вектора параметров 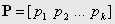 произвольной, в общем случае нелинейной функции
произвольной, в общем случае нелинейной функции 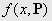 некоторым итерационным методом из условия минимизации функционала
некоторым итерационным методом из условия минимизации функционала  при заданном векторе начальных приближений
при заданном векторе начальных приближений 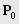 .
.
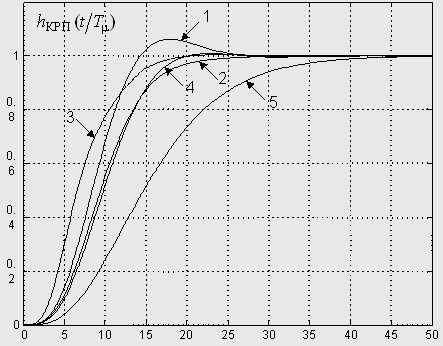
Рисунок 1 – Переходные функции КРП с параметрами (2) – 1, (3) – 2,
(4) – 3, (5) – 4, (6) – 5
Нелинейная функция может быть задана ссылкой на Simulink-модель.
Выполним поиск постоянных времени  по следующей методике:
по следующей методике:
1) разработаем Simulink-модель объекта регулирования (см. рис.2) и сохраним ее в файле srp.m:

Рисунок 2 – Simulink-модель замкнутого контура регулирования положения
2) cоставим MATLAB-функцию для расчета оптимизируемой функции времени посредством моделирования системы рис. 2:
function F = lsqSRP(T)
Tt = T(1); Tc = T(2); Tp = T(3);
opt = simset('solver','ode5','SrcWorkspace','Current', 'MaxStep', 0.05);
[t,x,y] = sim('srp',[0 50],opt); F = abs(1-y(:,1));
3) составим программу оптимизации:
T0=[2 4 8]
opt = optimset('LargeScale','off', 'Display','iter', 'TolX',1e-6, 'TolFun',1e-6);
T=lsqnonlin(@lsqSRP,T0,[],[],opt)
Tt = T(1), Tc = T(2), Tp = T(3)
В результате выполнения последней программы получены следующие параметры рассматриваемой системы:
 |
(4) |
Переходная функция КРП при таких параметрах представлена на рис.1 кривой 3. Для сравнения на рис. 1 представлены еще 2 переходные функции, соответствующие стандартным распределениям полюсов, обеспечивающим пренебрежительно малое перерегулирование (кривая 4 – распределение Бесселя) или полное его отсутствие (кривая 5 – биномиальное распределение) [1]. Переход от коэффициентов соответствующих стандартных нормированных полиномов к постоянным времени интегрирования разомкнутых контуров системы подчиненного регулирования положения осуществлялся по методике, изложенной в [1]. В результате применения этой методики получено: для распределения Бесселя
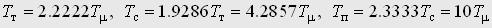 |
(5) |
и для биномиального распределения –
 . . |
(6) |
Сравнение полученных переходных функций наглядно демонстрирует преимущества настройки, полученной при помощи предложенной методики параметрической оптимизации. Кривая 3 имеет не только самое маленькое значение интегрального квадратичного отклонения переходной функции от заданного значения, но еще и самое высокое быстродействие при отсутствии перерегулирования. Следует отметить, что использование параметров (3), (4) и (5) изменяет настройку не только контура положения, но и контуров скорости и тока по сравнению с общепринятыми настройками контуров в составе СПР. При желании изменить настройку внешнего контура без изменения настройки внутренних контуров в рассматриваемой системе следует воспользоваться методикой структурного синтеза, изложенной в [1].
Перечень ссылок
- Толочко О.І. Аналіз та синтез електромеханічних систем зі спостерігачами стану. – Донецьк: Норд-Прес, 2004. – 298 с.
- Толочко О.И., Коцегуб П.Х., Розкаряка П.И. Применение метода стандартных полиномов при синтезе системы подчиненного регулирования положения // Вісник Східноукраїнського національного університету ім. В.Даля. – Луганськ. – 2007. – №11 (117). Ч.1. – С. 188-193.
Первоисточник: Сборник научных статей VIII Международной научно-технической конференции аспирантов и студентов – Донецк, ДонНТУ, 14-16 мая 2008 – С. 5-6
















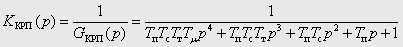 ,
, – постоянные времени интегрирования разомкнутых контуров положения, скорости и тока соответственно;
– постоянные времени интегрирования разомкнутых контуров положения, скорости и тока соответственно; 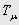 – малая некомпенсируемая постоянная времени привода.
– малая некомпенсируемая постоянная времени привода.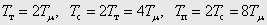
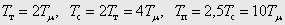
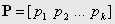 произвольной, в общем случае нелинейной функции
произвольной, в общем случае нелинейной функции 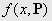 некоторым итерационным методом из условия минимизации функционала
некоторым итерационным методом из условия минимизации функционала  при заданном векторе начальных приближений
при заданном векторе начальных приближений 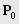 .
.
 по следующей методике:
по следующей методике:

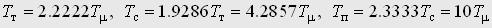
 .
.






