Яблонь В.П., Морозов Д.И., Полилов Е.В.
Украина Алчевск
Донбасский государственный технический университет
ОПТИМИЗАЦИЯ ДИАГРАММЫ ПОЗИЦИОННОГО ЭЛЕКТРОПРИВОДА ПО МИНИМУМУ ПОТЕРЬ ПРИ НЕИЗМЕННЫХ ДИНАМИЧЕСКИХ МОМЕНТАХ
В статье приведены результаты поиска оптимальной с точки зрения потерь в электроприводе диаграммы отработки заданного перемещения при неизменном динамическом моменте. Показано, что минимальные потери будут при отработке перемещения по трапецеидальной тахограмме с одинаковым временем разгона, торможения и установившегося движения.
In paper the results of search optimum from the point of view of losses in the electrical drive of the diagram of improvement of given moving at the constant dynamic moment are reduced. Is shown, that the minimum losses will be at improvement of moving on trapezoidal tachogram with equal time of acceleration, inhibiting action and constant driving.
Введение. На современном этапе развития и совершенствования технологических процессов предъявляются высокие требования не только к качеству переходных процессов, точностным характеристикам, диапазону регулирования скорости электромеханических систем, но и к их энергетическим показателям. Вопрос энергосбережения становится все более актуальным. В современном производстве весьма широко используются позиционные электроприводы, в которых на этапах пуска и торможения осуществляется стабилизация динамического момента (тока), а заданное перемещение отрабатывается по трапецеидальным или треугольным тахограммам. Темпы разгона и торможения при этом, как правило, выбираются, исходя из наиболее полного использования динамических возможностей электрической машины, что позволяет получить малое время отработки заданного перемещения, но это не всегда оправдано с энергетической точки зрения. Зачастую без нарушения технологических требований ко времени отработки заданного перемещения можно выбрать более рациональный с точки зрения энергетики режим работы позиционного механизма.
Анализ предыдущих исследований. В [1] авторами показано, что при отработке заданного перемещения по треугольной тахограмме потери в якорной цепи машины пропорциональны отношению времен отработки в третьей степени (без учета статической нагрузки). При учете последней выяснилось, что зависимость потерь от времени отработки перемещения имеет экстремальный характер. В [2] показано, что потребление реактивной энергии не растет, а снижается, несмотря на то, что при снижении темпов разгона и торможения уменьшается среднее значения косинуса угла управления за цикл. Это объясняется более быстрым темпом снижения потребляемой из сети энергии по сравнению с ростом угла регулирования. В [3] показано, что более выгодной по минимуму потерь в якорной цепи является не треугольная, а трапециидальная тахограмма. Но установившаяся скорость на такой тахограмме должна определяться не максимальной допустимой скоростью машины (традиционный подход), а рассчитываться, исходя из величины отрабатываемого перемещения и допустимого времени его отработки.
Цель работы. Получение расчетных соотношений для определения режимов отработки заданных перемещений при минимуме потерь в якорной цепи позиционных электроприводов, работающих со стабилизацией момента (тока) при пуске и торможении.
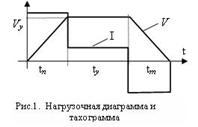
Материал и результаты исследований. При отработке заданного перемещения по трапецеидальной тахограмме (рис.1) потери в якорной цепи могут быть определены следующим выражением:
 , , |
(1) |
где  - кратности динамического
- кратности динамического  и статического
и статического  токов (моментов) машины;
токов (моментов) машины;  - номинальный ток и момент;
- номинальный ток и момент; 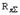 - суммарное сопротивление якорной цепи;
- суммарное сопротивление якорной цепи;  - соответственно время пуска, установившегося движения и торможения.
- соответственно время пуска, установившегося движения и торможения.
Для рассматриваемого случая стабилизации динамического тока (момента) времена пуска и торможения равны, поэтому, введя общее обозначение для времени переходного процесса 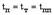 , после несложных преобразований из (1) получим следующее выражение:
, после несложных преобразований из (1) получим следующее выражение:
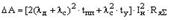 . . |
(2) |
Естественно, что площадь трапеции на рисунке 1 соответствует заданному перемещению  , которое может быть связано с приведенной тахограммой следующим выражением:
, которое может быть связано с приведенной тахограммой следующим выражением:
 , , |
(3) |
где установившееся значение скорости 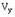 может быть связанно с кратностью динамического тока
может быть связанно с кратностью динамического тока  и временем переходного процесса
и временем переходного процесса  следующим образом:
следующим образом:
 . . |
(4) |
В выражении (4) через 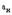 обозначено линейное ускорение, соответствующее номинальному моменту (току) машины. Подставив (4) в (3), получим выражение, определяющее время установившегося движения:
обозначено линейное ускорение, соответствующее номинальному моменту (току) машины. Подставив (4) в (3), получим выражение, определяющее время установившегося движения:
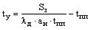 . . |
(5) |
Подставив (5) в (2), получим выражение, определяющее потери в якорной цепи машины  с заданным перемещением
с заданным перемещением  позиционного механизма:
позиционного механизма:
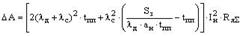 . . |
(6) |
Уравнение (6) определяет потери в якорной цепи машины 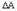 , как функцию двух переменных: кратности динамического тока (момента)
, как функцию двух переменных: кратности динамического тока (момента) 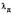 и времени переходного процесса
и времени переходного процесса . Исследуем данную функцию на экстремум:
. Исследуем данную функцию на экстремум:
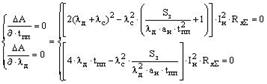 . . |
(7) |
Решение системы уравнений показывает, что функция (6) имеет экстремум в точке с координатами:
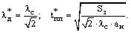 . . |
(8) |
Дальнейшие исследования функции двух переменных (6) показали, что найденный экстремум является минимумом, т.е. при задании динамического тока с кратностью  и длительности пуска и торможения
и длительности пуска и торможения 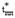 при отработке перемещения
при отработке перемещения  в якорной цепи приводной машины будет теряться минимум энергии. Найдем также значения длительности установившегося движения и величины установившейся скорости, соответствующие данному экстремуму. Подставив (8) в (5) и (4) получим:
в якорной цепи приводной машины будет теряться минимум энергии. Найдем также значения длительности установившегося движения и величины установившейся скорости, соответствующие данному экстремуму. Подставив (8) в (5) и (4) получим:
 , , |
(9) |
 . . |
(10) |
Сравнивая (8) и (9) можно сделать вывод, что при осуществлении движения по найденной оптимизированной по минимуму потерь тахограмме должно соблюдаться условие:
 . . |
(11) |
При этом общее время, затрачиваемое на осуществление перемещения  , составит:
, составит: 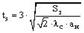 .
.
Выводы. В статье показано, что отработка перемещения позиционным механизмом с минимальными потерями в двигателе происходит при трапецеидальной тахограмме с одинаковыми продолжительностями разгона, установившегося движения и торможения. Данный результат справедлив при неизменности динамических моментов. Получены выражения для определения динамического момента, времени отработки перемещения и уровня установившейся скорости в зависимости от значения требуемого перемещения.
Литература.
- Полилов Е.В., Зеленов А.Б., Яблонь В.П., Морозов Д.И. Энергосбережение и оптимизация потерь в позиционных электроприводах // Електромашинобудування та електрообладнання. Тематичний випуск «Проблеми автоматизованого електропривода. Теорія і практика». – К.: Техніка, 2006. – С.315-319.
- Зеленов А.Б., Полилов Е.В., Яблонь В.П., Морозов Д.И. Потребление реактивной энергии позиционными электроприводами постоянного тока // Вестник Кременчугского государственного политехнического ун-та им. М. Остроградского. – Кременчуг: КГПУ. – Вып. 3/2007 (44), Ч1. – С. 76-78.
- Зеленов А.Б., Полилов Е.В., Яблонь В.П., Морозов Д.И. Энергосбережение и оптимизация потерь в позиционных электроприводах (часть 2) // Вестник Кременчугского государственного политехнического ун-та им. М. Остроградского. – Кременчуг: КГПУ. – Вып. 3/2007 (44), Ч2. – С. 82-87.
Первоисточник: http://paep2007.abacus.ua/default.aspx?id=paep_show_doc&doc=11399
















 ,
,
 - кратности динамического
- кратности динамического  и статического
и статического  токов (моментов) машины;
токов (моментов) машины;  - номинальный ток и момент;
- номинальный ток и момент; 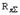 - суммарное сопротивление якорной цепи;
- суммарное сопротивление якорной цепи;  - соответственно время пуска, установившегося движения и торможения.
- соответственно время пуска, установившегося движения и торможения.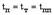 , после несложных преобразований из (1) получим следующее выражение:
, после несложных преобразований из (1) получим следующее выражение: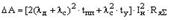 .
. , которое может быть связано с приведенной тахограммой следующим выражением:
, которое может быть связано с приведенной тахограммой следующим выражением:
 ,
,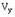 может быть связанно с кратностью динамического тока
может быть связанно с кратностью динамического тока  и временем переходного процесса
и временем переходного процесса  следующим образом:
следующим образом:
 .
.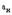 обозначено линейное ускорение, соответствующее номинальному моменту (току) машины. Подставив (4) в (3), получим выражение, определяющее время установившегося движения:
обозначено линейное ускорение, соответствующее номинальному моменту (току) машины. Подставив (4) в (3), получим выражение, определяющее время установившегося движения:
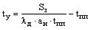 .
. с заданным перемещением
с заданным перемещением  позиционного механизма:
позиционного механизма:
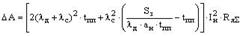 .
.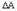 , как функцию двух переменных: кратности динамического тока (момента)
, как функцию двух переменных: кратности динамического тока (момента) 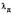 и времени переходного процесса
и времени переходного процесса . Исследуем данную функцию на экстремум:
. Исследуем данную функцию на экстремум:
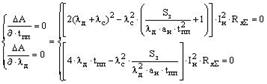 .
.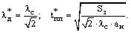 .
. и длительности пуска и торможения
и длительности пуска и торможения 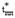 при отработке перемещения
при отработке перемещения  в якорной цепи приводной машины будет теряться минимум энергии. Найдем также значения длительности установившегося движения и величины установившейся скорости, соответствующие данному экстремуму. Подставив (8) в (5) и (4) получим:
в якорной цепи приводной машины будет теряться минимум энергии. Найдем также значения длительности установившегося движения и величины установившейся скорости, соответствующие данному экстремуму. Подставив (8) в (5) и (4) получим:
 ,
, .
. .
. , составит:
, составит: 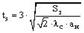 .
.






