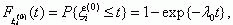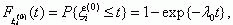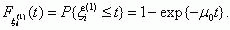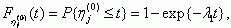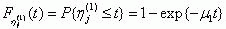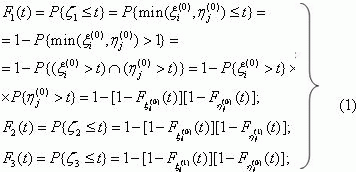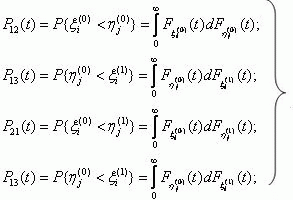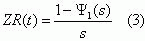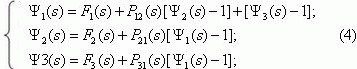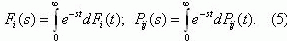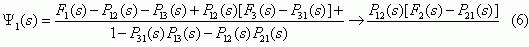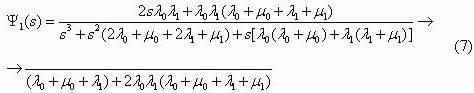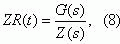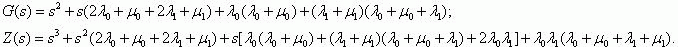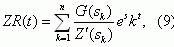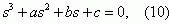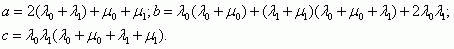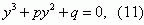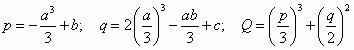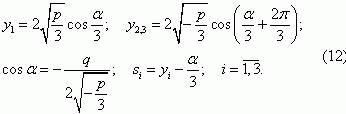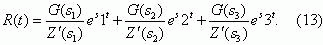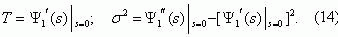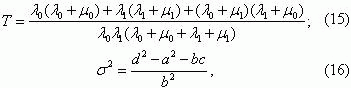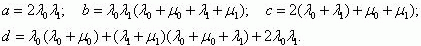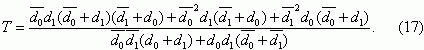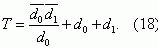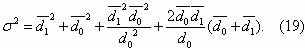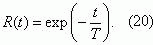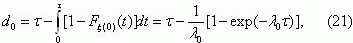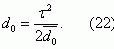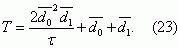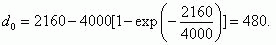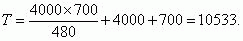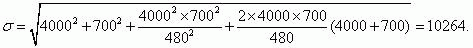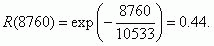КОВАЛЕВ А.П., БЕЛОУСЕНКО И.В., МУХА В.П., ШЕВЧЕНКО А.В._О надежности максимальных токовых защит, применяемых в сетях угольных шахт

О НАДЕЖНОСТИ МАКСИМАЛЬНЫХ ТОКОВЫХ ЗАЩИТ, ПРИМЕНЯЕМЫХ В СЕТЯХ УГОЛЬНЫХ ШАХТ

КОВАЛЕВ А.П., БЕЛОУСЕНКО И.В., МУХА В.П., ШЕВЧЕНКО А.В.

Предложена математическая модель надежности максимальной токовой защиты, которая учитывает частоту отказов в схеме защиты, сроки профилактики и частоту появления коротких замыканий на защищаемом объекте в зоне ее действия. Даны примеры расчета.

Ключевые слова: шахтовые сети, максимальная токовая защита, надежность, математическая модель

При оценке надежности релейной защиты следует различать два вида отказов – несрабатывание при наличии на входе соответствующего воздействия (отказ срабатывания) и срабатывание при его отсутствии – ложные, излишние срабатывания [1, 2].

Последствия нарушения надежности по селективности и безотказности для шахтных максимальных токовых защит различны. Ложные и излишние срабатывания приводят, как правило, к отключению потребителей участка и в большинстве случаев к незначительному материальному ущербу. Отказ срабатывания защиты приводит к выгораемым коротким замыканиям (КЗ), за время существования которых в подземных кабельных сетях угольных шахт окружающие кабель горючие предметы (угольная пыль, деревянная и т.д.) обычно загораются [3].
Отказ максимальной токовой защиты можно представить как результат совмещения во времени двух случайных событий: повреждение защищаемого объекта (КЗ в кабельной сети или защищаемом электроборудовании, при котором действие защиты обязательно) и отказ в схеме защиты [4].
Случайный интервал времени между последовательными повреждениями схемы максимальной токовой защиты обозначим через ξ_i⁽⁰) .Случайное время нахождения схемы защиты в необнаруженном отказавшем состоянии обозначим ξ_i⁽¹⁾, i=1,2,…,n. Это время, в основном, зависит от периодичности проверок и квалификации обслуживающего персонала.
Случайный интервал времени между последовательными КЗ в зоне действия защиты обозначим через η_j⁽⁰⁾, а время существования КЗ (время срабатывания защиты) будем рассматривать как случайную величину η_j⁽¹⁾ j=1,2,…,m.
При случайном совпадении независимых интервалов времени ξ_i⁽¹⁾ и η_j⁽¹⁾ происходит отказ защиты или выгораемое КЗ, или иначе: выгораемое КЗ в сети наступает всякий раз, когда случайным образом схема защиты наступает всякий раз, когда случайным образом схема защиты наступает всякий раз, когда случайным образом схема защиты находится в отказавшем состоянии (повреждена, установка защиты затрублена, защита отключена) и в это время в зоне действия рассматриваемой защиты происходит КЗ.
Задача состоит в определении среднего времени Т до первого отказа защиты, что то же до первого выгораемого КЗ, дисперсии этого времени σ² и вероятности безотказного функционирования R (t).
Для решения поставленной задачи примем ряд допущений и положений. Устройства защиты могут выходить из строя только тогда, когда они находятся в режиме ожидания. Цели к моменту возникновения КЗ в сети защита находилась в исправном состоянии, то маловероятно, чтобы она вышла из строя, находясь в режиме тревоги [4 – 6].После каждого отказа устройство защиты полностью восстанавливается (в шахтном электрооборудовании блоки защит в большинстве своем съемные), отказы в схемах защиты выявляются и устраняются только в результате профилактических проверок.
Изменение состояний схемы защиты во времени представим в виде случайной функции ξ(t), которая имеет два значения: «0» и «1». Состояние «0» означает, что в схеме защиты повреждений нет и «1» – в схеме защиты имеются повреждения. Последовательно чередующиеся случайные интервалы времени ξ₀⁽⁰⁾, ξ₁⁽⁰⁾,…, ξ_i⁽⁰) ,…, ξ_n⁽⁰) отражают работоспособное состояние схемы, ξ ₀⁽¹⁾, ξ₁⁽¹⁾,…, ξ_i⁽¹),…, ξ_n⁽¹⁾ – неработоспособное.
Пусть все ξ_i⁽⁰) имеют одно и то же распределение

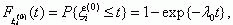
а все ξ_i⁽¹⁾– распределение

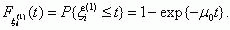
Величина λ₀ есть интенсивность отказов в схемах защиты, а μ₀ – интенсивность восстановления схем защиты. Величины ξ_i⁽⁰) и η_i⁽¹) взаимнонезависимы.
Состояние объекта защиты описывается аналогичной случайной функцией η(t), которая имеет также два состояния: «0» – в защищаемом объекте нет повреждений, приводящих к КЗ, «1» – произошло КЗ. Последовательно чередующиеся случайные интервалы времени между короткими замыканиями обозначим через η₀⁽⁰⁾, η₁⁽⁰⁾,…, η_j⁽⁰⁾,…, η_n ⁽⁰⁾, а длительность существования КЗ (длительность срабатывания защиты) – через η₀ ⁽¹⁾, η₁⁽¹⁾,…, η_j⁽¹⁾,…, η_n⁽¹⁾ имеют распределение

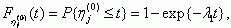
а вce η_j⁽¹⁾ – распределение

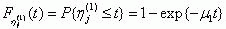
Величина λ₁ есть интенсивность появления КЗ в защищаемом элементе, а μ₁– интенсивность отключения поврежденного элемента схемой защиты. Величины η_j⁽⁰⁾ и η_j⁽¹⁾ также взаимнонеиависимы.
Опасность возникновения отказов защиты наступает в момент встречи процессов ξ(t) и η(t) в состояниях «1», т. е. когда защита из-за отказов в схеме не может отключить поврежденный элемент сети (см. рисунок).

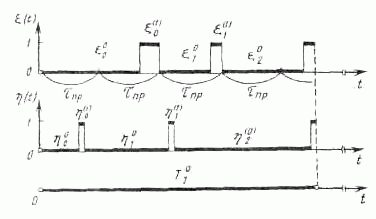
Будем считать, что в начальный момент ξ(0)=η(0) = 0, т.е. в схеме защиты повреждений нет и на защищаемом объекте отсутствуют КЗ. После того как отказ защиты произошел, ситуация возобновляется и промежуток времени между первым и вторым отказом защиты T₂⁽⁰⁾ является случайной величиной, не зависящей от T₁⁽⁰⁾, но имеющей то же статистическое распределение, и. в частности, то же среднее значение Т и т.д.
Пару процессов [ξ(t), η(t)] рассмотрим как полумарковский процесс (ПМП) [7] с четырьмя состояниями: e₁ (0,0) – в схеме защиты повреждений нет на защищаемом объекте не наблюдается КЗ; е₂ (0,1) – в схеме защиты повреждений нет; на защищаемом объекте произошло КЗ; е₃ (1,0) – повреждение в схеме защиты; на защищаемом объекте нет КЗ; е₄(1,1) – повреждение в схеме защиты, на защищаемом объекте возникло КЗ.
Множество состояний защиты Е разобьем на два подмножества, таким образом, что E₊∪E_- , Е₊∩Е_-=Ø, где E₊{e₁, e₂ , e₃} – множество безопасных состояний защиты, E_- {е₄} – отказовое состояние защиты.
Время пребывания защиты в состоянии е₁ (0,0) определяется наименьшим из времен ξ_i⁽⁰⁾,η_j⁽⁰⁾ т.е. ζ₁=min{ξ_i⁽⁰⁾,η_j⁽⁰⁾ } время пребывания защиты в состоянии е₂ (0,1) определяется наименьшим из времен ξ_i⁽⁰⁾ и η_j⁽¹⁾, т.е. ζ₂=min{ξ_i⁽⁰⁾,η_j⁽¹⁾}, а время нахождения в состоянии е₃ (1,0) определяется как ζ₃ =min{ξ_i⁽¹⁾,η_j⁽⁰⁾}.
Функция распределения времени нахождения защиты в каждом из e_i=1,2,3 состояний определяется следующим образом:

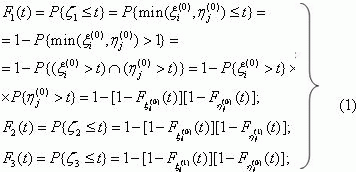
Вероятность переходов системы из состояния е₁ в состояние е_j за время не более t определим следующим образом [8]:

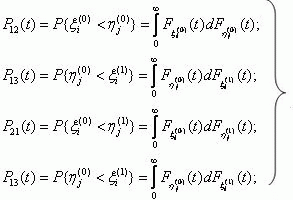
Вероятность безопасного функционирования защиты R(t) в интервале времени [0, t] определится как вероятность пребывания ПМП в подмножестве Е₊ в течение времени t при условии, что в момент t = 0 процесс находится в состоянии e₁.
Для определении вероятности R(t) вначале находится преобразование Лапласа-Стильтьеса Ψ(s), а затем - преобразование Лапласа искомой вероятности безотказного функционирования [9]

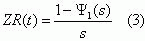
Для нахождения Ψ (s) используем общую систему уравнений, впервые полученную в [10]. В нашем случае система уравнений примет вид

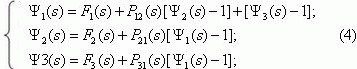
где F_i(s) и P_ij(s) – преобразование Лапласа-Стильтьеса функции распределения F_i(t) времени пребывания ПМП в состоянии е, и переходных вероятностей P_ij(t) соответственно:

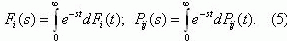
Решая систему уравнений (4) относительно Ψ(s), получим

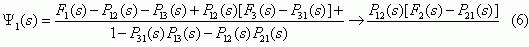
Подставляя функции распределения случайных величин ξ_i⁽⁰⁾,ξ_j⁽⁰⁾ η_i⁽¹⁾,η_j⁽¹⁾ в формулу (1) и (2) и используя формулу (5), получим выражение

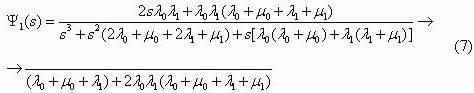
Подставив Ψ (s) из выражения (7) в (3) получим

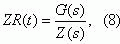
где

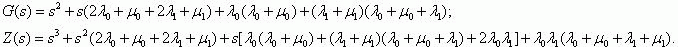
Для получения обратного преобразования Лапласа используем формулу из [11]:

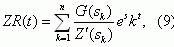
где s_k – корни уравнения Z'(s) = 0.
Для нашего случая Z' (s) примет вид

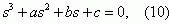
где

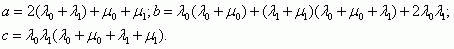
Подстановкой s=y-a/3 приводим кубическое уравнение неполному виду [12]:

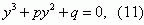
где

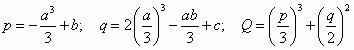
Для описанной задачи Q<0 и р<0, тогда корни кубического уравнения (10) определятся следующим образом:

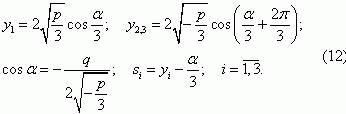
Подставляя значение корней s₁, s₂, s₃ в формулу (9), получим

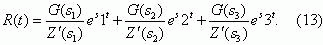
Среднее время до первого отказа защиты Т и дисперсию σ² этого времени найдем, используя известные соотношения [9]

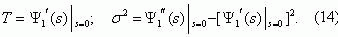
Используя формулу (7), находим, что

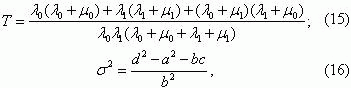
где

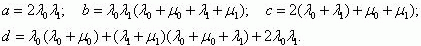
Если обозначить через d₀=1/λ₀ – среднее время нахождения схемы защиты в исправном состоянии, d₀=1/μ₀ – среднее время нахождения схемы защиты в отказавшем состоянии, d₁=1/λ₁, – средний интервал времени между появлениями КЗ в защищаемой сети, d₁ =1/μ₀– среднее время существования КЗ в зоне действия рассматриваемой максимальной токовой защиты, то формулу (15) можно представить виде

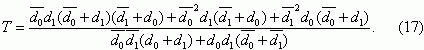
Учитывая, что для максимальных токовых защит выполняются следующие соотношения d₁<< d₁, d₁<< d₀, d₀<< d₁, то формулу (17) можно упростить:

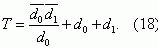
При этих же условиях формула (16) примет вид

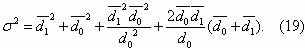
Вероятность безоткатной работы защиты R(t), полученную с помощью формул (8)–(13), с достаточной для практических расчетов точностью можно заменить экспоненциальной функцией при соблюдении условия T/σ≈1

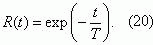
Среднее время нахождения схемы защиты необнаруженном отказавшем состоянии определить следующим образом [13]:

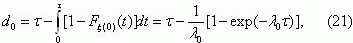
где τ_пр – заданный действующими нормативными документами интервал времени между проверками средств защиты.
Для случая когда τ_пр/d₀<0,1, формула [21] примет вид

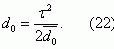
Подставив формулу (22) в формулу (18), получим

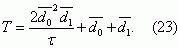
Пример 1.
Определить вероятность безотказной работы в течение t = 8760 ч максимальной токовой защиты к пускателе ПВИР-63, питающем удаленный маломощный двигатель лебедки. Чувствительность максимальной токовой защиты, находящейся и групповом автоматическом выключателе АВ-320, недостаточна, чтобы обеспечить продольное резервирование максимальной токовой защиты указанного пускателя при случайно происшедших КЗ на отходящей от пускателя кабельной линии. Реле утечки в трансформаторной подстанции TСШВП 400/6-0.69 находится в отказавшем состоянии. Исходные данные: средний интервал времени между отказами схемы максимальной токовой защиты (отказы в схеме выключателя в результате профилактических проверок) d₀ = 4000 ч: интервал времени между проверками схемы максимальной токовой защиты &tau_пр= 2160 ч; средний интервал времени между появлениями КЗ на рассматриваемой кабельной линии d₁ = 700ч.
Пользуясь формулой (21), определим среднее время нахождения схемы защиты в необнаруженном отказавшем состоянии:

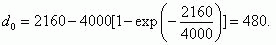
Используя формулу (18), находим среднее время безотказной работы максимальной токовой защиты:

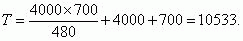
Определим σ пользуясь формулой (19);

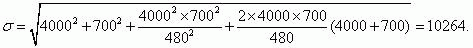
Функция вероятности безотказной работы R (t) будет определяться с помощью формулы (20), поскольку выполняется условие T/σ≈1

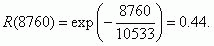
Пример 2.
Пользуясь исходными данными примера 1, определить, во сколько раз увеличится надежность максимальной токовой защиты, если схему защиты проверять через τ =720 ч.
Пользуясь формулой (21), находим, что d₀ = 80 ч. С помощью формулы (18) находим T₁ = 39700 ч. Используя формулу (20), получим R₁ (8760)=0,8
Следовательно при уменьшении сроков профилактики (для нашего примера) схемы защиты в 3 раза среднее время безотказной работы защиты увеличится в 3,77 раза, а вероятность отказа защиты за время t = 8760 ч увеличится в 2.8 раза.

Вывод.
Предложенная математическая модель надежности максимальной токовой защиты, применяемой в подземных сетях угольных шахт, отличается от известных: она учитывает среднее значение времени нахождения схемы защиты в необнаруженном отказавшем состоянии и частоту ее профилактических работ.

СПИСОК ЛИТЕРАТУРЫ

1. РИПС Я.А. Расчет эксплуатационной надежности релейной защиты. – Электричество, 1968, № 4.
2.Надежность систем энергетики. Терминология. – Сб.рекомендуемых терминов – М.: Наука, 1980.
3. КОВАЛЕНКО.М.И., ЗРЕЛЫЙ.В.Т. , ХОРОЛЬСКИЙ Н.Ф. и дрПрофилактика пожаров и взрывов в угольных шахтах . – М.; Недра, 1983.
4.ФАБРИКАНТ В.П. О применении теории надежности к оценке устройств релейной зашиты. – Электричестно. 1965, № 9.
5.СМИРНОВ Э. П. Влияние профилактического контроля на результирующую надежность релейной защиты. – Электричество, 1965. № 4.
6. ПАРЗАМ А.Б. Отклик на статью Э.П. Смирнова. Электричество, 1967. №8.
7. КОРОЛЮК B.C., ТУРБИН А.Ф. Полумарковские процессы и их приложения. – Киев.: Наукова думка, 1976.
8. БОРОДИН С.М., ВАСИЛЕНКО О.И., МАРЧЕНКО Б.Г. Расчет и планирование испытаний систем на надежность. – Киев.: Наукова думка, 1970.
9. КРЕДЕННЕР Б.П. Прогнозирование надежности систем с временной избыточностью. – Киев: Наукова думка. 1978.
10. КОРОЛЮК B.C. Время пребывания полумарковского процесса в фиксированном множестве состояний, – УМЖ, 1965, № 3.
11. МАРТЫНЕНКО B.C. Операционное исчисление. – Киев.: Высшая школа. 1973.
12. БРОНШТЕЙН И.П., СЕМЕНДЯЕВ К.Л. Справочник но математике для инженеров и учащихся вузов, – М.: Наука. 1986.
13. КОВАЛЕВ А.П. О проблемах оценки безопасности электротехнических объектов. – Электричество, 1991, № 8.

Авторы:
КОВАЛЕВ АЛЕКСАНДР ПЕТРОВИЧ окончил электротехнический факультет Донецкого политехнического института (ДПИ) в 1972 г. и математический факультет Донецкого госуниверситета (ДГУ) в 1977 г. В 1992 г. защитил докторскую диссертацию по специальности «Техника безопасности и противопожарная техника» в ДПИ. Доцент ДПИ.
МУХА ВАЛЕНТИН ПАВЛОВИЧ окончил электротехнический факультет ДПИ в 1966 г. В 1975 г. защитил кандидатскую диссертацию по специальности «Энергетические системы и управление ими» в Ереванском политехническом институте. Доцент ДПИ.
ШЕВЧЕНКО АНДРЕЙ ВАДИМОВИЧ окончил математический факультет ДГУ в 1975 г. Ассистент ДПИ.
БЕЛОУСЕНКО ИГОРЬ ВЛАДИМИРОВИЧ окончил энергетический факультет ДИН в 1981 г. В 1991 г. защитил кандидатскую диссертацию по специальности: Энергетические системы и управление ими в ДПИ. Главный технолог РАО «Газпром».

Вернуться в библиотеку