МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ УСТАНОВИВШИХСЯ РЕЖИМОВ РАБОТЫ АСИНХРОННЫХ ЭЛЕКТРОДВИГАТЕЛЕЙ ПРИ НАЛИЧИИ В НИХ ДЕФЕКТОВ
Полковниченко Д.В., к.т.н., асс.
Донецкий национальный технический университет
Существующие методы диагностики технического состояния электродвигателей оказываются малоэффективными для применения на работающей машине и не могут предупреждать о возникновении дефектов на ранней стадии их возникновения.
Главная трудность в решении данной задачи заключается в том, что пока недостаточно исследованы от-дельные неисправности электрических машин на предмет получения диагностической информации и не определены специальные информативные параметры или признаки (диагностические параметры), характеризующие изменение величин и характеристик электромагнитного, вибрационного и акустического процессов их функ-ционирования при возникновении соответствующих неисправностей [1].
На основании анализа повреждений электродвигателей, а также по результатам экспериментальных исследований [2], был сделан вывод об универсальности использования в качестве диагностического параметра тока обратной последовательности (ОП). Его универсальность заключается в том, что возникновение практически любого дефекта приводит к изменению тока ОП.
Для проверки сделанных заключений и получения зависимостей тока ОП от степени развития дефектов были проведены исследования установившихся режимов работы асинхронных электродвигателей (АД) с корот-козамкнутым ротором (КЗР) на математической модели. Одной из задач исследований был выбор математических моделей АД для определения пороговых значений диагностических параметров при возникновении различных видов дефектов и проверка степени их адекватности, т.к. от этого в большой степени зависит достоверность оценки технического состояния электродвигателя.
Для исследования установившихся режимов работы АД при наличии поврежденных стержней КЗР была использована математическая модель [3] для расчета мгновенных значений токов и напряжений, составленная на основе полных дифференциальных уравнений в фазных координатах статора (a, b, c) и в фазных координа-тах ротора (1, 2, ..., n) с учетом того, что глубокопазный ротор представлен в виде эквивалентного двухклеточного. При этом количество фаз в обмотке ротора равняется числу короткозамкнутых стержней ротора. Отличи-тельной особенностью данной модели является то, что она может быть применена для глубокопазных АД с учетом явления вытеснения тока в роторе.
Исходными данными для математического моделирования являются параметры двухконтурной схемы замещения АД, расчет которых производится по каталожным данным АД в соответствии с методикой, приведенной в работе [4].
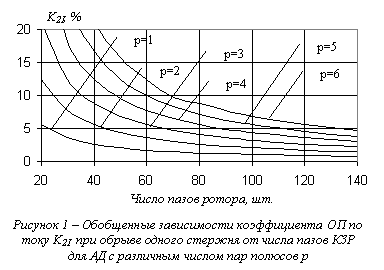
На основании исследований, проведенных для АД различных типов и с различными конструктивными особенностями, были получены обобщенные зависимости коэффициента ОП по току (относительное содержание тока ОП в токе статора) при обрыве одного стержня от количества пазов КЗР для АД различного конструктивного исполнения в номинальном режиме работы (рис.1). Расчеты для различных коэффициентов загрузки АД (0,5-1,0) показали, что величина коэффициента ОП по току K2I примерно прямо пропорциональна коэффициенту загрузки АД Кзагр
Известно, что при обрыве стержня КЗР происходит снижение потребляемой активной мощности АД и одновременно уменьшается частота вращения ротора, т.е. увеличивается скольжение АД. Таким образом, целесообразным является использование в качестве диагностического параметра отношения активной мощности на валу АД к скольжению P/S.
Анализ полученных зависимостей отношения P/S от количества оборванных стержней КЗР при различ-ных коэффициентах загрузки АД показал, что величина отношения P/S при обрыве одного стержня с достаточ-ной степенью точности может рассчитываться по выражению
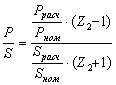
где Р, Рном - соответственно расчетная и номинальная мощности АД;
S, Sрасч - соответственно расчетное и номинальное скольжение АД;
Z2 - число пазов КЗР.
Таким образом, проведенные исследования показали, что коэффициент ОП по току и отношение P/S обладают хорошей информативностью при диагностировании технического состояния КЗР. Диагноз "обрыв стержня КЗР" ставится в случае превышения диагностическими параметрами своих пороговых значений. При этом частота тока ОП является функцией скольжения S и определяется по выражению [5]
f2=f1(1-2S),
где f1 - частота питающего напряжения.
Для исследования зависимости диагностических параметров в рабочем режиме АД при наличии витко-вых замыканий в обмотке статора использовалась модель, описание которой приведено в работе [6]. Модель основана на определении собственных и взаимных индуктивностей контуров обмотки статора. Это связано с тем, что при замыкании небольшого числа витков обе части обмотки статора расположены в одних и тех же пазах, поэтому их взаимоиндукция велика. Индуктивность замкнутых витков мала, и при относительно небольшом токе в остальной части обмотки ток в поврежденных витках может достичь больших значений.
Исследования, проведенные на математической модели для АД различной мощности серий и типов ДАЗО2 16-го и 18-го габаритов, ДАЗО4, АТД2, АТД4, А и АЗ 12-го и 13-го габаритов, АВ и АВК, показали, что на начальной стадии развития виткового замыкания (т.е. в области действия системы диагностики) зависимость коэффициента ОП по току K2I от количества замкнувшихся витков с достаточной степенью точности может быть представлена кривой, приведенной на рис.2.

Заключение о возникновении виткового замыкания в обмотке статора делается в случае увеличения тока ОП и одновременного увеличения фазных токов АД. При этом ток в поврежденной фазе увеличивается значительно больше, чем в "здоровых" фазах, а частота тока ОП равна частоте питающего напряжения.
Обрыв параллельных ветвей обмотки статора также приводит к появлению тока ОП. При расчете обры-вов параллельных ветвей обмотки статора приняты следующие допущения:
- сопротивления всех параллельных ветвей всех фаз приняты равными;
- взаимоиндуктивности между параллельными ветвями одной фазы равны;
- взаимоиндуктивности между ветвями различных фаз равны.
В результате проведенных расчетов была получена система из трех уравнений, где неизвестными являются токи в параллельных ветвях фаз ![]() ,
,![]() ,
,![]() :
:
w - угловая частота сети;
М1 - взаимоиндуктивность между ветвями одной фазы;
М2 - взаимоиндуктивность между ветвями разных фаз;
m - число параллельных ветвей обмотки статора;
na, nb, nc - число оборванных ветвей по фазам статора.
По найденным из (1) токам в параллельных ветвях обмотки статора определяется величина тока ОП.
На рис.3 приведены обобщенные зависимости коэффициента ОП по току K2I от количества оборванных параллельных ветвей обмотки статора для АД с различным числом таких ветвей (2, 3, 4).
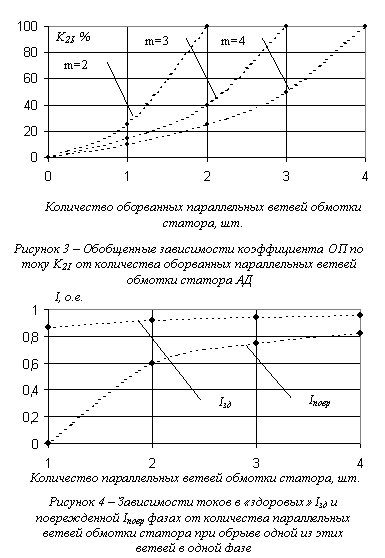
Приведенные результаты показывают, что ток ОП позволяет с большой точностью выявлять обрыв параллельных ветвей статорных обмоток электродвигателей. Частота тока ОП при этом равна частоте питающего напряжения. Поврежденная фаза находится по величине тока в этой фазе. Величина тока в поврежденной фазе меньше, чем в "здоровых" фазах. Зависимости токов в "здоровых" Iзд и поврежденной Iповр фазах от количества параллельных ветвей обмотки статора при обрыве одной из этих ветвей в одной фазе приведены на рис.4 и также могут использоваться при постановке диагноза о техническом состояния АД.
Сравнение результатов экспериментальных исследований [2] и математического моделирования установившихся режимов работы опытного АД при наличии в нем дефектов показало, что при обрыве стержней КЗР отклонение величины коэффициента ОП по току K2I не превышает 10,4 %, а отклонение отношения P/S - 6,8 %. Отклонение величины коэффициента ОП по току K2I при витковых замыканиях в обмотке статора не превышает 10 %. Полученные результаты подтверждают адекватность использованных математических моделей, а также возможность построения принципов диагностики с их использованием.
Литература
- Гашимов М.А. Логические методы диагностики технического состояния электрических машин // Электричество. - 1999. - № 7. - С.20-26.
- Гребченко Н.В., Полковниченко Д.В. Экспериментальные исследования установившихся режимов работы асинхронных электродвигателей при наличии в них дефектов // Сборник научных трудов ДонГТУ. Серия: электротехника и энергетика, выпуск 17. - Донецк: ДонГТУ. - 2000. -С. 110-114.
- Нури Абделбассет. Диагностика короткозамкнутых роторов асинхронных электроприводов электро-технических комплексов: Дис... канд. техн. наук: 05.09.03. - Донецк, 1997. - 135 с.
- Сивокобыленко В.Ф., Костенко В.И. Математическое моделирование электродвигателей собственных нужд электрических станций. Учебное пособие. - Донецк.: ДПИ, 1979. - 110 с.
- Гашимов М.А., Аскеров Н.А. Выявление неисправности стержней ротора асинхронных электродвигателей // Электрические станции. - 1984. - № 8. - С. 60-66.
- Ипатов П.М., Домбровский В.В., Цирлин Ю.Л. Витковые замыкания в петлевых обмотках асинхронных машин // Вестник электропромышленности. - 1962. - № 7. - С. 36-43