To get back in a library
Translation of the article
Kinetics of H2S and CO2 in Aqueous Solutions of MEA, DEA, and MDEA
To determine the rate of absorption of CO2 and H2S in an aqueous amine solution,
the rates of reaction of these gases in the solution must be estimated. This article presents an extensive literature survey on the
kinetics of the reactions of CO2 and H2S in aqueous solutions of pure MEA, DEA, and MDEA and blends
of MEA/MDEA and DEA/MDEA is presented. The important reactions and the mechanism by which these reactions occur in the
liquid film are clarified.
The concentrations of the hydronium, hydroxide, sulfide, and carbonate ions that are generated from these reactions
are relatively small. It is therefore, safe to assume that the concentrations of these ions in the liquid film are equal
to their respective bulk concentrations. The concentration of water in the liquid film can also be considered unaffected
by the kinetics of the reactions in the liquid film. The liquid film concentrations of the remaining species must be
considered to accurately calculate the rate of absorption of CO2 and H2S.
1. Mechanism of the H2S Reaction in Aqueous Solutions of Alkanolamine
H2S reacts with MEA, DEA, or MDEA to form hydrogen sulfide and protonated
amine according to the following
reactions:
MEA:
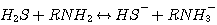
(3.1)
DEA:
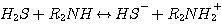
(3.2)
MDEA:
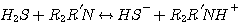
(3.3)
The mechanism of each of these reactions involves a proton transfer. Therefore, all these
reactions are considered
instantaneous with infinite reaction rate. The liquid film concentrations of the reactants and products of these
reactions are at local equilibrium:
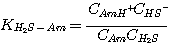
(3.4)
where the subscript Am refers to MEA, DEA, or MDEA. The equilibrium constants, KH2S-Am, are
related to the equilibrium constants defined in Chapter 2 by:
MEA:
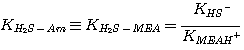
(3.5)
DEA:
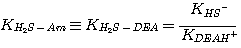
(3.6)
MDEA:
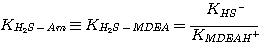
(3.7)
The rate of absorption of H2S in an aqueous solution containing a single amine
can be determined analytically.
This was done by Onda et al. 1970. They used the two-film theory to derive a general analytical expression of the
enhancement factor for systems comprising a single instantaneous chemical reaction. For systems containing blends of
amines, the amines compete to absorb H2S. The governing differential equations for these systems are too
complicated to be solved analytically. The equilibrium constant of the sulfide formation reaction (equation 2.5)
is too small to affect the concentration of the bisulfide in the liquid film. Therefore, ignoring this reaction in the
liquid film hardly affects the calculation of the H2S absorption rate.
2. Mechanism of the CO2 Reaction in Aqueous Solutions of Alkanolamine
In any aqueous solution, CO2 reacts with water and hydroxide according
to the following reactions:
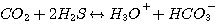
(3.8)
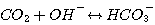
(3.9)
The CO2 consumption by reaction 3.8 is first order with respect
to CO2. The forward rate constant of
this reaction was correlated as a function of temperature by Pinsent and coworkers (Pinsent et al., 1956):
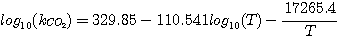
(3.10)
The rate of disappearance of CO2 by reaction 3.9 follows elementary
kinetics and can be expressed by:
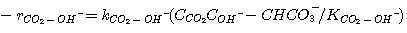
(3.11)
Astarita et al. (1983) studied the effect of ionic strength on the rate constant,
kCO2-OH-. They extended the expression originally presented by Sherwood et al.
(1975) to include the ionic strength:
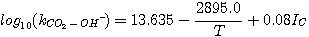
(3.12)
where IC is the concentration-based ionic strength given by:
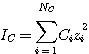
(3.13)
Reactions (3.8) and (3.9) are very slow compared to the CO2
reactions with MEA or DEA especially for
CO2 loadings less than 0.5. Ignoring these reactions does not affect the calculation of the rate of
absorption of CO2. Hence, the liquid film concentration of the bicarbonate ion is constant in systems
containing only MEA or DEA. On the other hand, MDEA is believed to catalyze these reactions. As a result, ignoring the
change of the liquid film concentration of the bicarbonate in systems containing MDEA might lead to an error in the
calculation of the CO2 absorption rate.
2.1 CO2 Reaction with MEA and DEA
The absorption of CO2 in aqueous solutions of
MEA and DEA has been extensively studied in the literature.
Several techniques have been used to collect the kinetics data. These include laminar jet falling film, rapid mixing,
falling film, diffusion across a porous media, and stirred reactor. Descriptions of the methodology and experimental set
up are given by Van Krevelen and Hoftijzer (1948), Nunge and Gill (1963), Coldrey and Harris (1976), Alvarez et al.
(1980), Glasscock (1990), Hogendoorn et al. (1993), and Ko and Li (2000).
The MEA reaction with CO2 has been studied
by several researchers including Astarita 1961, Leder 1971,
Sada et al. 1976, Hikita et al. 1977, Laddha and Danckwerts, 1981 and Blauwhoff et al. 1984. There is a general agreement
among the researchers that the reaction of CO2 with MEA follows a second order kinetics. The second order rate
constant of this reaction was correlated as a function of temperature by Hikita et al. 1977. The revision of the data made
by Blauwhoff et al. 1984 and Barth et al. 1986 supported the results of Hikita et al. 1977.
Blanc and Demarais (1984) revised the data and the
proposed mechanisms for the rate of reaction of CO2
with DEA. They realized that the researchers results vary significantly. The dependence of the reaction rate on the
concentration of DEA was reported as first or second order. The reported rate constants were also not comparable.
Blauwhoff et al. (1984) revised the reported kinetics data for this system. They concluded that the reaction rate of
CO2 with DEA is too complicated to be interpreted by a simple kinetic model. They further showed that the
zwitterion mechanism reconciles most of the CO2-DEA published kinetics data. The zwitterion mechanism was
adopted by Glasscock (1990) to represent the kinetics data of CO2 in primary and secondary alkanolamines.
This mechanism was originally proposed by Caplow in 1968 and introduced to the chemical engineering literature by
Danckwerts in 1979. According to this mechanism, CO2 reacts with MEA or DEA to form an unstable zwitterion, Z.
The zwitterion is instantaneously neutralized by any base, Bi, present in the solution to form the amine
carbamate and a protonated base, BiH+:
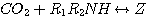
(3.14)

(3.15)
where Z ≡ R1R2NH+, R1 ≡ CH3CH2OH,
and R2 ≡ H and R1 for MEA and DEA, respectively. Reaction 3.14 is the rate controlling step;
hence the rate of disappearance of CO2 is given by:
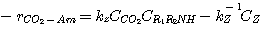
(3.16)
Since, the zwitterion is unstable, its rate of
formation is zero:

(3.17)
Solving for the concentration of the zwitterion
gives:
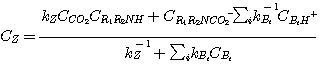
(3.18)
Substituting equation 3.18 into equation 3.16 and rearranging gives:

(3.19)
Equation 3.19 can be simplified by relating the groups of rate constants to their corresponding equilibrium
constants as follows. Consider the water reaction with a base:
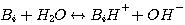
(3.20)
This reaction involves a proton transfer, therefore, the reactants and products of this reaction are always at local
equilibrium:
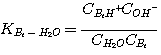
(3.21)
or:
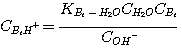
(3.22)
The amine can act as a base and reacts with water according to:

(3.23)
where:

(3.24)
Combining reactions 3.20 and 3.23 gives:
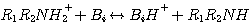
(3.25)
where:
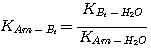
(3.26)
The reaction of amine with the zwitterion is given by:

(3.27)
Combining reactions 3.25 and 3.27 gives:
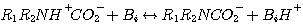
(3.28)
Comparing reactions 3.15 and 3.28 gives:
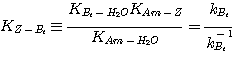
(3.29)
or:
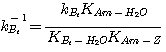
(3.30)
Adding reactions 3.14 and 3.15 and replacing with amine gives:

(3.31)
where:

(3.32)
or:

(3.33)
Substituting equations 3.24 and 3.33 into equation 3.30 gives:

(3.34)
Substituting equations 3.34 and 3.22 into equation 3.19 and rearranging gives:

(3.35)
The second term in the numerator of equation (3.35) represents the concentration of CO2 that is in is in
equilibrium with the amine, amine carbamate and protonated amine based on reaction 3.31. Hence, this equation can be
rewritten as:

(3.36)
As mentioned, the kinetics data for the CO2-MEA system follows a second order kinetics. Equation 3.35 is
reduced to
the second order form if the second term in the denominator is ignored in comparison to the first term, leading to:

(3.37)
The second order rate constant given by Hikita et al. 1977 will be used in this study to compute the CO2
absorption rate for systems containing MEA. This rate constant is expressed as a function of temperature by:
MEA:

(3.38)
In contrast, the first term in the denominator of equation (3.35) is negligible compared to the second term for the
CO2-DEA system:
DEA:

(3.39)
Equation 3.39 was used by Laddha and Danckwerts 1981, Blauwhoff et al. (1984), Versteeg and Van Swaaij (1988),
Critchfield (1988), and Glasscock (1990) to describe the kinetics data for the CO2-DEA system.
Glasscock (1990) assumed that the amine and the water are the only bases that contribute to the neutralization of the
zwitterion. The CO2-DEA rate expression reported by Glasscock 1990 will be utilized in this study.
This expression is given by
DEA:

(3.40)
The rate constants reported by Glasscock (1990) were extracted from the fit of the kinetics data and expressed as
functions of temperature according to

(3.41)

(3.42)
2.2 CO2 Reaction with MDEA
CO2 reacts indirectly with MDEA in the presence of water to form bicarbonate and protonated MDEA.
Three different mechanisms have been proposed for this reaction (Barth et al. 1981). The first mechanism suggests that
MDEA neutralizes the species formed by the CO2-water reactions (reactions 3.8 and 3.9). The second mechanism
assumes that MDEA associates with water before reacting with CO2:

(3.43)
The third mechanism follows the zwitterion mechanism described earlier for MEA and DEA:

(3.44)
The zwitterion formed immediately reacts with water and hydroxide to produce respectively bicarbonate and protonated
MDEA and bicarbonate and MDEA according to:
The third mechanism follows the zwitterion mechanism described earlier for MEA and DEA:

(3.45)

(3.46)
Adopting the third mechanism and following the procedure developed earlier for MEA and DEA, the following expression is
obtained for the rate of reaction of CO2 with MDEA:

(3.47)
Combining reactions 3.44 with 3.45 and 3.44 with 3.46 gives:

(3.48)

(3.49)
Reaction 3.48 can also be obtained from combinations of the following reactions:

(3.50)

(3.51)
Hence

(3.52)
Since reaction 3.50 is instantaneous, its products and reactants are at local equilibrium:

(3.53)
Therefore:

(3.54)
Reaction 3.49 can be obtained by combining the instantaneous water dissociation reaction (equation 2.1) with reaction
3.51 to obtain:

(3.55)
or:

(3.56)
Substituting equations 3.54 and 3.56 into equation 3.47 and rearranging gives:

(3.57)
or:

(3.58)
Similar to the derivation of MEA and DEA, the second term in the numerator of equation 3.58 represents the
concentration of CO2 which is in equilibrium with the bicarbonate and the hydroxide ions:

(3.59)
Equation 3.58 is a general rate expression for the reaction of CO2 with MDEA or any tertiary amine.
Depending on the magnitude of the second term of the denominator of this equation, one can obtain two limiting forms:

The rate expression in this case reduces to:

(3.60)
This form is essentially the expression, which would have been obtained if the second mechanism were used.
Many investigators including Haimor et al. (1987), Critchfield (1988), Tomcej et al. (1989), Little et al. (1990),
Rangwala et al. (1992), and Ko and Li (2000) adopted this form to fit the rate data of the CO2-MDEA system.
The rate constant of the reaction is given as a function of temperature by:

(3.61)
Comparison among the published values of the rate constant at 298.15 K shows a variation between 2.5 and 8.8
lit/mol/sec.

In this case the rate expression is given by:

(3.62)
Glasscock (1990) showed that this form reconciled the published rate data better.
He used activities instead of concentrations to obtain the rate constants. In the current study, the rate expression
represented by the first form (equation 3.60) with the rate constant reported by Critchfield (1988) will be used to model
the kinetics of the CO2 reaction with MDEA. The rate constant reported by Critchfield (1988) is given by:

(3.63)
2.3 CO2 Reaction with Blends of MEA-MDEA and DEA-MDEA
The absorption of CO2 in aqueous solution of blends of MEA-MDEA and DEA-MDEA was studied by Glasscock et
al. (1990), Versteeg et al. (1990), Rangwala et al. (1992), and Hagewiesche et al. (1995). Critchfield showed that the
interaction between MDEA and MEA is insignificant. Therefore the rate expressions (equation 3.37) for MEA and
(equation 3.60) for MDEA are still applicable for the mixture MEA-MDEA. However, for systems containing DEA and MDEA,
the latter acts as another base that neutralizes the zwitterion formed from the reaction of CO2 with DEA.
Hence, The CO2-DEA rate expression for systems containing DEA and MDEA should be corrected by adding the
contribution of MDEA to the neutralization of the zwitterion:
DEA/MDEA:

(3.64)

A value of 468 m6/kmol2/sec was reported in the thesis of Glasscock (1990) for the rate
constant k'R1R2R3N. In this work, this value will be used for
any temperature to compute the absorption rate of CO2in systems containing blends of DEA and MDEA.
Following the suggestion of Glasscock (1990), the effect of MDEA on the rate of reaction of CO2with MEA
will be ignored.
1. Mechanism of the H2S Reaction in Aqueous Solutions of Alkanolamine
H2S reacts with MEA, DEA, or MDEA to form hydrogen sulfide and protonated
amine according to the following
reactions:
MEA:
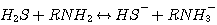
(3.1)
DEA:
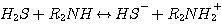
(3.2)
MDEA:
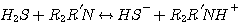
(3.3)
The mechanism of each of these reactions involves a proton transfer. Therefore, all these
reactions are considered
instantaneous with infinite reaction rate. The liquid film concentrations of the reactants and products of these
reactions are at local equilibrium:
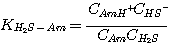
(3.4)
where the subscript Am refers to MEA, DEA, or MDEA. The equilibrium constants, KH2S-Am, are
related to the equilibrium constants defined in Chapter 2 by:
MEA:
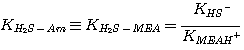
(3.5)
DEA:
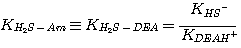
(3.6)
MDEA:
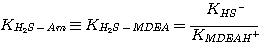
(3.7)
The rate of absorption of H2S in an aqueous solution containing a single amine
can be determined analytically.
This was done by Onda et al. 1970. They used the two-film theory to derive a general analytical expression of the
enhancement factor for systems comprising a single instantaneous chemical reaction. For systems containing blends of
amines, the amines compete to absorb H2S. The governing differential equations for these systems are too
complicated to be solved analytically. The equilibrium constant of the sulfide formation reaction (equation 2.5)
is too small to affect the concentration of the bisulfide in the liquid film. Therefore, ignoring this reaction in the
liquid film hardly affects the calculation of the H2S absorption rate.
2. Mechanism of the CO2 Reaction in Aqueous Solutions of Alkanolamine
In any aqueous solution, CO2 reacts with water and hydroxide according
to the following reactions:
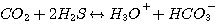
(3.8)
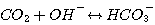
(3.9)
The CO2 consumption by reaction 3.8 is first order with respect
to CO2. The forward rate constant of
this reaction was correlated as a function of temperature by Pinsent and coworkers (Pinsent et al., 1956):
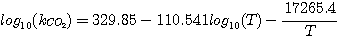
(3.10)
The rate of disappearance of CO2 by reaction 3.9 follows elementary
kinetics and can be expressed by:
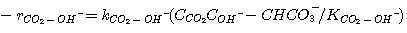
(3.11)
Astarita et al. (1983) studied the effect of ionic strength on the rate constant,
kCO2-OH-. They extended the expression originally presented by Sherwood et al.
(1975) to include the ionic strength:
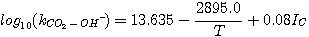
(3.12)
where IC is the concentration-based ionic strength given by:
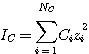
(3.13)
Reactions (3.8) and (3.9) are very slow compared to the CO2
reactions with MEA or DEA especially for
CO2 loadings less than 0.5. Ignoring these reactions does not affect the calculation of the rate of
absorption of CO2. Hence, the liquid film concentration of the bicarbonate ion is constant in systems
containing only MEA or DEA. On the other hand, MDEA is believed to catalyze these reactions. As a result, ignoring the
change of the liquid film concentration of the bicarbonate in systems containing MDEA might lead to an error in the
calculation of the CO2 absorption rate.
2.1 CO2 Reaction with MEA and DEA
The absorption of CO2 in aqueous solutions of
MEA and DEA has been extensively studied in the literature.
Several techniques have been used to collect the kinetics data. These include laminar jet falling film, rapid mixing,
falling film, diffusion across a porous media, and stirred reactor. Descriptions of the methodology and experimental set
up are given by Van Krevelen and Hoftijzer (1948), Nunge and Gill (1963), Coldrey and Harris (1976), Alvarez et al.
(1980), Glasscock (1990), Hogendoorn et al. (1993), and Ko and Li (2000).
The MEA reaction with CO2 has been studied
by several researchers including Astarita 1961, Leder 1971,
Sada et al. 1976, Hikita et al. 1977, Laddha and Danckwerts, 1981 and Blauwhoff et al. 1984. There is a general agreement
among the researchers that the reaction of CO2 with MEA follows a second order kinetics. The second order rate
constant of this reaction was correlated as a function of temperature by Hikita et al. 1977. The revision of the data made
by Blauwhoff et al. 1984 and Barth et al. 1986 supported the results of Hikita et al. 1977.
Blanc and Demarais (1984) revised the data and the
proposed mechanisms for the rate of reaction of CO2
with DEA. They realized that the researchers results vary significantly. The dependence of the reaction rate on the
concentration of DEA was reported as first or second order. The reported rate constants were also not comparable.
Blauwhoff et al. (1984) revised the reported kinetics data for this system. They concluded that the reaction rate of
CO2 with DEA is too complicated to be interpreted by a simple kinetic model. They further showed that the
zwitterion mechanism reconciles most of the CO2-DEA published kinetics data. The zwitterion mechanism was
adopted by Glasscock (1990) to represent the kinetics data of CO2 in primary and secondary alkanolamines.
This mechanism was originally proposed by Caplow in 1968 and introduced to the chemical engineering literature by
Danckwerts in 1979. According to this mechanism, CO2 reacts with MEA or DEA to form an unstable zwitterion, Z.
The zwitterion is instantaneously neutralized by any base, Bi, present in the solution to form the amine
carbamate and a protonated base, BiH+:
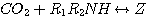
(3.14)

(3.15)
where Z ≡ R1R2NH+, R1 ≡ CH3CH2OH,
and R2 ≡ H and R1 for MEA and DEA, respectively. Reaction 3.14 is the rate controlling step;
hence the rate of disappearance of CO2 is given by:
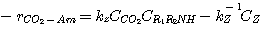
(3.16)
Since, the zwitterion is unstable, its rate of
formation is zero:

(3.17)
Solving for the concentration of the zwitterion
gives:
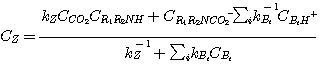
(3.18)
Substituting equation 3.18 into equation 3.16 and rearranging gives:

(3.19)
Equation 3.19 can be simplified by relating the groups of rate constants to their corresponding equilibrium
constants as follows. Consider the water reaction with a base:
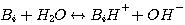
(3.20)
This reaction involves a proton transfer, therefore, the reactants and products of this reaction are always at local
equilibrium:
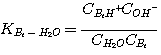
(3.21)
or:
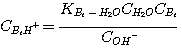
(3.22)
The amine can act as a base and reacts with water according to:

(3.23)
where:

(3.24)
Combining reactions 3.20 and 3.23 gives:
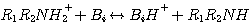
(3.25)
where:
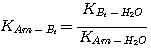
(3.26)
The reaction of amine with the zwitterion is given by:

(3.27)
Combining reactions 3.25 and 3.27 gives:
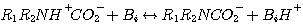
(3.28)
Comparing reactions 3.15 and 3.28 gives:
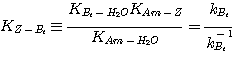
(3.29)
or:
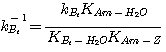
(3.30)
Adding reactions 3.14 and 3.15 and replacing with amine gives:

(3.31)
where:

(3.32)
or:

(3.33)
Substituting equations 3.24 and 3.33 into equation 3.30 gives:

(3.34)
Substituting equations 3.34 and 3.22 into equation 3.19 and rearranging gives:

(3.35)
The second term in the numerator of equation (3.35) represents the concentration of CO2 that is in is in
equilibrium with the amine, amine carbamate and protonated amine based on reaction 3.31. Hence, this equation can be
rewritten as:

(3.36)
As mentioned, the kinetics data for the CO2-MEA system follows a second order kinetics. Equation 3.35 is
reduced to
the second order form if the second term in the denominator is ignored in comparison to the first term, leading to:

(3.37)
The second order rate constant given by Hikita et al. 1977 will be used in this study to compute the CO2
absorption rate for systems containing MEA. This rate constant is expressed as a function of temperature by:
MEA:

(3.38)
In contrast, the first term in the denominator of equation (3.35) is negligible compared to the second term for the
CO2-DEA system:
DEA:

(3.39)
Equation 3.39 was used by Laddha and Danckwerts 1981, Blauwhoff et al. (1984), Versteeg and Van Swaaij (1988),
Critchfield (1988), and Glasscock (1990) to describe the kinetics data for the CO2-DEA system.
Glasscock (1990) assumed that the amine and the water are the only bases that contribute to the neutralization of the
zwitterion. The CO2-DEA rate expression reported by Glasscock 1990 will be utilized in this study.
This expression is given by
DEA:

(3.40)
The rate constants reported by Glasscock (1990) were extracted from the fit of the kinetics data and expressed as
functions of temperature according to

(3.41)

(3.42)
2.2 CO2 Reaction with MDEA
CO2 reacts indirectly with MDEA in the presence of water to form bicarbonate and protonated MDEA.
Three different mechanisms have been proposed for this reaction (Barth et al. 1981). The first mechanism suggests that
MDEA neutralizes the species formed by the CO2-water reactions (reactions 3.8 and 3.9). The second mechanism
assumes that MDEA associates with water before reacting with CO2:

(3.43)
The third mechanism follows the zwitterion mechanism described earlier for MEA and DEA:

(3.44)
The zwitterion formed immediately reacts with water and hydroxide to produce respectively bicarbonate and protonated
MDEA and bicarbonate and MDEA according to:
The third mechanism follows the zwitterion mechanism described earlier for MEA and DEA:

(3.45)

(3.46)
Adopting the third mechanism and following the procedure developed earlier for MEA and DEA, the following expression is
obtained for the rate of reaction of CO2 with MDEA:

(3.47)
Combining reactions 3.44 with 3.45 and 3.44 with 3.46 gives:

(3.48)

(3.49)
Reaction 3.48 can also be obtained from combinations of the following reactions:

(3.50)

(3.51)
Hence

(3.52)
Since reaction 3.50 is instantaneous, its products and reactants are at local equilibrium:

(3.53)
Therefore:

(3.54)
Reaction 3.49 can be obtained by combining the instantaneous water dissociation reaction (equation 2.1) with reaction
3.51 to obtain:

(3.55)
or:

(3.56)
Substituting equations 3.54 and 3.56 into equation 3.47 and rearranging gives:

(3.57)
or:

(3.58)
Similar to the derivation of MEA and DEA, the second term in the numerator of equation 3.58 represents the
concentration of CO2 which is in equilibrium with the bicarbonate and the hydroxide ions:

(3.59)
Equation 3.58 is a general rate expression for the reaction of CO2 with MDEA or any tertiary amine.
Depending on the magnitude of the second term of the denominator of this equation, one can obtain two limiting forms:

The rate expression in this case reduces to:

(3.60)
This form is essentially the expression, which would have been obtained if the second mechanism were used.
Many investigators including Haimor et al. (1987), Critchfield (1988), Tomcej et al. (1989), Little et al. (1990),
Rangwala et al. (1992), and Ko and Li (2000) adopted this form to fit the rate data of the CO2-MDEA system.
The rate constant of the reaction is given as a function of temperature by:

(3.61)
Comparison among the published values of the rate constant at 298.15 K shows a variation between 2.5 and 8.8
lit/mol/sec.

In this case the rate expression is given by:

(3.62)
Glasscock (1990) showed that this form reconciled the published rate data better.
He used activities instead of concentrations to obtain the rate constants. In the current study, the rate expression
represented by the first form (equation 3.60) with the rate constant reported by Critchfield (1988) will be used to model
the kinetics of the CO2 reaction with MDEA. The rate constant reported by Critchfield (1988) is given by:

(3.63)
2.3 CO2 Reaction with Blends of MEA-MDEA and DEA-MDEA
The absorption of CO2 in aqueous solution of blends of MEA-MDEA and DEA-MDEA was studied by Glasscock et
al. (1990), Versteeg et al. (1990), Rangwala et al. (1992), and Hagewiesche et al. (1995). Critchfield showed that the
interaction between MDEA and MEA is insignificant. Therefore the rate expressions (equation 3.37) for MEA and
(equation 3.60) for MDEA are still applicable for the mixture MEA-MDEA. However, for systems containing DEA and MDEA,
the latter acts as another base that neutralizes the zwitterion formed from the reaction of CO2 with DEA.
Hence, The CO2-DEA rate expression for systems containing DEA and MDEA should be corrected by adding the
contribution of MDEA to the neutralization of the zwitterion:
DEA/MDEA:

(3.64)

A value of 468 m6/kmol2/sec was reported in the thesis of Glasscock (1990) for the rate
constant k'R1R2R3N. In this work, this value will be used for
any temperature to compute the absorption rate of CO2in systems containing blends of DEA and MDEA.
Following the suggestion of Glasscock (1990), the effect of MDEA on the rate of reaction of CO2with MEA
will be ignored.
| MEA: |
|
(3.1) |
| DEA: |
|
(3.2) |
| MDEA: |
|
(3.3) |
The mechanism of each of these reactions involves a proton transfer. Therefore, all these
reactions are considered
instantaneous with infinite reaction rate. The liquid film concentrations of the reactants and products of these
reactions are at local equilibrium:
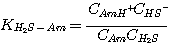
(3.4)
where the subscript Am refers to MEA, DEA, or MDEA. The equilibrium constants, KH2S-Am, are
related to the equilibrium constants defined in Chapter 2 by:
MEA:
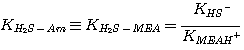
(3.5)
DEA:
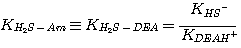
(3.6)
MDEA:
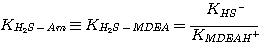
(3.7)
The rate of absorption of H2S in an aqueous solution containing a single amine
can be determined analytically.
This was done by Onda et al. 1970. They used the two-film theory to derive a general analytical expression of the
enhancement factor for systems comprising a single instantaneous chemical reaction. For systems containing blends of
amines, the amines compete to absorb H2S. The governing differential equations for these systems are too
complicated to be solved analytically. The equilibrium constant of the sulfide formation reaction (equation 2.5)
is too small to affect the concentration of the bisulfide in the liquid film. Therefore, ignoring this reaction in the
liquid film hardly affects the calculation of the H2S absorption rate.
2. Mechanism of the CO2 Reaction in Aqueous Solutions of Alkanolamine
In any aqueous solution, CO2 reacts with water and hydroxide according
to the following reactions:
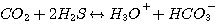
(3.8)
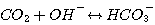
(3.9)
The CO2 consumption by reaction 3.8 is first order with respect
to CO2. The forward rate constant of
this reaction was correlated as a function of temperature by Pinsent and coworkers (Pinsent et al., 1956):
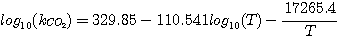
(3.10)
The rate of disappearance of CO2 by reaction 3.9 follows elementary
kinetics and can be expressed by:
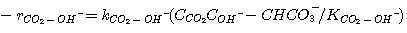
(3.11)
Astarita et al. (1983) studied the effect of ionic strength on the rate constant,
kCO2-OH-. They extended the expression originally presented by Sherwood et al.
(1975) to include the ionic strength:
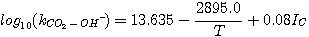
(3.12)
where IC is the concentration-based ionic strength given by:
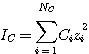
(3.13)
Reactions (3.8) and (3.9) are very slow compared to the CO2
reactions with MEA or DEA especially for
CO2 loadings less than 0.5. Ignoring these reactions does not affect the calculation of the rate of
absorption of CO2. Hence, the liquid film concentration of the bicarbonate ion is constant in systems
containing only MEA or DEA. On the other hand, MDEA is believed to catalyze these reactions. As a result, ignoring the
change of the liquid film concentration of the bicarbonate in systems containing MDEA might lead to an error in the
calculation of the CO2 absorption rate.
2.1 CO2 Reaction with MEA and DEA
The absorption of CO2 in aqueous solutions of
MEA and DEA has been extensively studied in the literature.
Several techniques have been used to collect the kinetics data. These include laminar jet falling film, rapid mixing,
falling film, diffusion across a porous media, and stirred reactor. Descriptions of the methodology and experimental set
up are given by Van Krevelen and Hoftijzer (1948), Nunge and Gill (1963), Coldrey and Harris (1976), Alvarez et al.
(1980), Glasscock (1990), Hogendoorn et al. (1993), and Ko and Li (2000).
The MEA reaction with CO2 has been studied
by several researchers including Astarita 1961, Leder 1971,
Sada et al. 1976, Hikita et al. 1977, Laddha and Danckwerts, 1981 and Blauwhoff et al. 1984. There is a general agreement
among the researchers that the reaction of CO2 with MEA follows a second order kinetics. The second order rate
constant of this reaction was correlated as a function of temperature by Hikita et al. 1977. The revision of the data made
by Blauwhoff et al. 1984 and Barth et al. 1986 supported the results of Hikita et al. 1977.
Blanc and Demarais (1984) revised the data and the
proposed mechanisms for the rate of reaction of CO2
with DEA. They realized that the researchers results vary significantly. The dependence of the reaction rate on the
concentration of DEA was reported as first or second order. The reported rate constants were also not comparable.
Blauwhoff et al. (1984) revised the reported kinetics data for this system. They concluded that the reaction rate of
CO2 with DEA is too complicated to be interpreted by a simple kinetic model. They further showed that the
zwitterion mechanism reconciles most of the CO2-DEA published kinetics data. The zwitterion mechanism was
adopted by Glasscock (1990) to represent the kinetics data of CO2 in primary and secondary alkanolamines.
This mechanism was originally proposed by Caplow in 1968 and introduced to the chemical engineering literature by
Danckwerts in 1979. According to this mechanism, CO2 reacts with MEA or DEA to form an unstable zwitterion, Z.
The zwitterion is instantaneously neutralized by any base, Bi, present in the solution to form the amine
carbamate and a protonated base, BiH+:
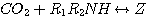
(3.14)

(3.15)
where Z ≡ R1R2NH+, R1 ≡ CH3CH2OH,
and R2 ≡ H and R1 for MEA and DEA, respectively. Reaction 3.14 is the rate controlling step;
hence the rate of disappearance of CO2 is given by:
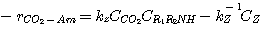
(3.16)
Since, the zwitterion is unstable, its rate of
formation is zero:

(3.17)
Solving for the concentration of the zwitterion
gives:
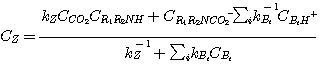
(3.18)
Substituting equation 3.18 into equation 3.16 and rearranging gives:

(3.19)
Equation 3.19 can be simplified by relating the groups of rate constants to their corresponding equilibrium
constants as follows. Consider the water reaction with a base:
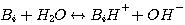
(3.20)
This reaction involves a proton transfer, therefore, the reactants and products of this reaction are always at local
equilibrium:
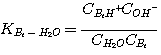
(3.21)
or:
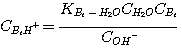
(3.22)
The amine can act as a base and reacts with water according to:

(3.23)
where:

(3.24)
Combining reactions 3.20 and 3.23 gives:
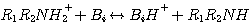
(3.25)
where:
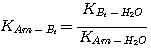
(3.26)
The reaction of amine with the zwitterion is given by:

(3.27)
Combining reactions 3.25 and 3.27 gives:
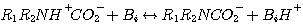
(3.28)
Comparing reactions 3.15 and 3.28 gives:
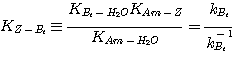
(3.29)
or:
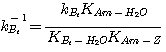
(3.30)
Adding reactions 3.14 and 3.15 and replacing with amine gives:

(3.31)
where:

(3.32)
or:

(3.33)
Substituting equations 3.24 and 3.33 into equation 3.30 gives:

(3.34)
Substituting equations 3.34 and 3.22 into equation 3.19 and rearranging gives:

(3.35)
The second term in the numerator of equation (3.35) represents the concentration of CO2 that is in is in
equilibrium with the amine, amine carbamate and protonated amine based on reaction 3.31. Hence, this equation can be
rewritten as:

(3.36)
As mentioned, the kinetics data for the CO2-MEA system follows a second order kinetics. Equation 3.35 is
reduced to
the second order form if the second term in the denominator is ignored in comparison to the first term, leading to:

(3.37)
The second order rate constant given by Hikita et al. 1977 will be used in this study to compute the CO2
absorption rate for systems containing MEA. This rate constant is expressed as a function of temperature by:
MEA:

(3.38)
In contrast, the first term in the denominator of equation (3.35) is negligible compared to the second term for the
CO2-DEA system:
DEA:

(3.39)
Equation 3.39 was used by Laddha and Danckwerts 1981, Blauwhoff et al. (1984), Versteeg and Van Swaaij (1988),
Critchfield (1988), and Glasscock (1990) to describe the kinetics data for the CO2-DEA system.
Glasscock (1990) assumed that the amine and the water are the only bases that contribute to the neutralization of the
zwitterion. The CO2-DEA rate expression reported by Glasscock 1990 will be utilized in this study.
This expression is given by
DEA:

(3.40)
The rate constants reported by Glasscock (1990) were extracted from the fit of the kinetics data and expressed as
functions of temperature according to

(3.41)

(3.42)
2.2 CO2 Reaction with MDEA
CO2 reacts indirectly with MDEA in the presence of water to form bicarbonate and protonated MDEA.
Three different mechanisms have been proposed for this reaction (Barth et al. 1981). The first mechanism suggests that
MDEA neutralizes the species formed by the CO2-water reactions (reactions 3.8 and 3.9). The second mechanism
assumes that MDEA associates with water before reacting with CO2:

(3.43)
The third mechanism follows the zwitterion mechanism described earlier for MEA and DEA:

(3.44)
The zwitterion formed immediately reacts with water and hydroxide to produce respectively bicarbonate and protonated
MDEA and bicarbonate and MDEA according to:
The third mechanism follows the zwitterion mechanism described earlier for MEA and DEA:

(3.45)

(3.46)
Adopting the third mechanism and following the procedure developed earlier for MEA and DEA, the following expression is
obtained for the rate of reaction of CO2 with MDEA:

(3.47)
Combining reactions 3.44 with 3.45 and 3.44 with 3.46 gives:

(3.48)

(3.49)
Reaction 3.48 can also be obtained from combinations of the following reactions:

(3.50)

(3.51)
Hence

(3.52)
Since reaction 3.50 is instantaneous, its products and reactants are at local equilibrium:

(3.53)
Therefore:

(3.54)
Reaction 3.49 can be obtained by combining the instantaneous water dissociation reaction (equation 2.1) with reaction
3.51 to obtain:

(3.55)
or:

(3.56)
Substituting equations 3.54 and 3.56 into equation 3.47 and rearranging gives:

(3.57)
or:

(3.58)
Similar to the derivation of MEA and DEA, the second term in the numerator of equation 3.58 represents the
concentration of CO2 which is in equilibrium with the bicarbonate and the hydroxide ions:

(3.59)
Equation 3.58 is a general rate expression for the reaction of CO2 with MDEA or any tertiary amine.
Depending on the magnitude of the second term of the denominator of this equation, one can obtain two limiting forms:

The rate expression in this case reduces to:

(3.60)
This form is essentially the expression, which would have been obtained if the second mechanism were used.
Many investigators including Haimor et al. (1987), Critchfield (1988), Tomcej et al. (1989), Little et al. (1990),
Rangwala et al. (1992), and Ko and Li (2000) adopted this form to fit the rate data of the CO2-MDEA system.
The rate constant of the reaction is given as a function of temperature by:

(3.61)
Comparison among the published values of the rate constant at 298.15 K shows a variation between 2.5 and 8.8
lit/mol/sec.

In this case the rate expression is given by:

(3.62)
Glasscock (1990) showed that this form reconciled the published rate data better.
He used activities instead of concentrations to obtain the rate constants. In the current study, the rate expression
represented by the first form (equation 3.60) with the rate constant reported by Critchfield (1988) will be used to model
the kinetics of the CO2 reaction with MDEA. The rate constant reported by Critchfield (1988) is given by:

(3.63)
2.3 CO2 Reaction with Blends of MEA-MDEA and DEA-MDEA
The absorption of CO2 in aqueous solution of blends of MEA-MDEA and DEA-MDEA was studied by Glasscock et
al. (1990), Versteeg et al. (1990), Rangwala et al. (1992), and Hagewiesche et al. (1995). Critchfield showed that the
interaction between MDEA and MEA is insignificant. Therefore the rate expressions (equation 3.37) for MEA and
(equation 3.60) for MDEA are still applicable for the mixture MEA-MDEA. However, for systems containing DEA and MDEA,
the latter acts as another base that neutralizes the zwitterion formed from the reaction of CO2 with DEA.
Hence, The CO2-DEA rate expression for systems containing DEA and MDEA should be corrected by adding the
contribution of MDEA to the neutralization of the zwitterion:
DEA/MDEA:

(3.64)

A value of 468 m6/kmol2/sec was reported in the thesis of Glasscock (1990) for the rate
constant k'R1R2R3N. In this work, this value will be used for
any temperature to compute the absorption rate of CO2in systems containing blends of DEA and MDEA.
Following the suggestion of Glasscock (1990), the effect of MDEA on the rate of reaction of CO2with MEA
will be ignored.
|
|
(3.4) |
where the subscript Am refers to MEA, DEA, or MDEA. The equilibrium constants, KH2S-Am, are related to the equilibrium constants defined in Chapter 2 by:
| MEA: |
|
(3.5) |
| DEA: |
|
(3.6) |
| MDEA: |
|
(3.7) |
The rate of absorption of H2S in an aqueous solution containing a single amine
can be determined analytically.
This was done by Onda et al. 1970. They used the two-film theory to derive a general analytical expression of the
enhancement factor for systems comprising a single instantaneous chemical reaction. For systems containing blends of
amines, the amines compete to absorb H2S. The governing differential equations for these systems are too
complicated to be solved analytically. The equilibrium constant of the sulfide formation reaction (equation 2.5)
is too small to affect the concentration of the bisulfide in the liquid film. Therefore, ignoring this reaction in the
liquid film hardly affects the calculation of the H2S absorption rate.
2. Mechanism of the CO2 Reaction in Aqueous Solutions of Alkanolamine
In any aqueous solution, CO2 reacts with water and hydroxide according
to the following reactions:
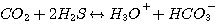
(3.8)
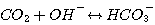
(3.9)
The CO2 consumption by reaction 3.8 is first order with respect
to CO2. The forward rate constant of
this reaction was correlated as a function of temperature by Pinsent and coworkers (Pinsent et al., 1956):
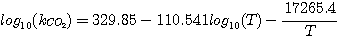
(3.10)
The rate of disappearance of CO2 by reaction 3.9 follows elementary
kinetics and can be expressed by:
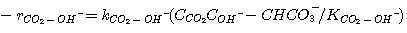
(3.11)
Astarita et al. (1983) studied the effect of ionic strength on the rate constant,
kCO2-OH-. They extended the expression originally presented by Sherwood et al.
(1975) to include the ionic strength:
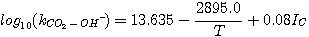
(3.12)
where IC is the concentration-based ionic strength given by:
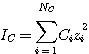
(3.13)
Reactions (3.8) and (3.9) are very slow compared to the CO2
reactions with MEA or DEA especially for
CO2 loadings less than 0.5. Ignoring these reactions does not affect the calculation of the rate of
absorption of CO2. Hence, the liquid film concentration of the bicarbonate ion is constant in systems
containing only MEA or DEA. On the other hand, MDEA is believed to catalyze these reactions. As a result, ignoring the
change of the liquid film concentration of the bicarbonate in systems containing MDEA might lead to an error in the
calculation of the CO2 absorption rate.
2.1 CO2 Reaction with MEA and DEA
The absorption of CO2 in aqueous solutions of
MEA and DEA has been extensively studied in the literature.
Several techniques have been used to collect the kinetics data. These include laminar jet falling film, rapid mixing,
falling film, diffusion across a porous media, and stirred reactor. Descriptions of the methodology and experimental set
up are given by Van Krevelen and Hoftijzer (1948), Nunge and Gill (1963), Coldrey and Harris (1976), Alvarez et al.
(1980), Glasscock (1990), Hogendoorn et al. (1993), and Ko and Li (2000).
The MEA reaction with CO2 has been studied
by several researchers including Astarita 1961, Leder 1971,
Sada et al. 1976, Hikita et al. 1977, Laddha and Danckwerts, 1981 and Blauwhoff et al. 1984. There is a general agreement
among the researchers that the reaction of CO2 with MEA follows a second order kinetics. The second order rate
constant of this reaction was correlated as a function of temperature by Hikita et al. 1977. The revision of the data made
by Blauwhoff et al. 1984 and Barth et al. 1986 supported the results of Hikita et al. 1977.
Blanc and Demarais (1984) revised the data and the
proposed mechanisms for the rate of reaction of CO2
with DEA. They realized that the researchers results vary significantly. The dependence of the reaction rate on the
concentration of DEA was reported as first or second order. The reported rate constants were also not comparable.
Blauwhoff et al. (1984) revised the reported kinetics data for this system. They concluded that the reaction rate of
CO2 with DEA is too complicated to be interpreted by a simple kinetic model. They further showed that the
zwitterion mechanism reconciles most of the CO2-DEA published kinetics data. The zwitterion mechanism was
adopted by Glasscock (1990) to represent the kinetics data of CO2 in primary and secondary alkanolamines.
This mechanism was originally proposed by Caplow in 1968 and introduced to the chemical engineering literature by
Danckwerts in 1979. According to this mechanism, CO2 reacts with MEA or DEA to form an unstable zwitterion, Z.
The zwitterion is instantaneously neutralized by any base, Bi, present in the solution to form the amine
carbamate and a protonated base, BiH+:
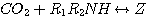
(3.14)

(3.15)
where Z ≡ R1R2NH+, R1 ≡ CH3CH2OH,
and R2 ≡ H and R1 for MEA and DEA, respectively. Reaction 3.14 is the rate controlling step;
hence the rate of disappearance of CO2 is given by:
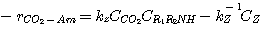
(3.16)
Since, the zwitterion is unstable, its rate of
formation is zero:

(3.17)
Solving for the concentration of the zwitterion
gives:
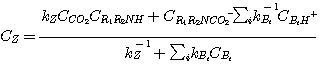
(3.18)
Substituting equation 3.18 into equation 3.16 and rearranging gives:

(3.19)
Equation 3.19 can be simplified by relating the groups of rate constants to their corresponding equilibrium
constants as follows. Consider the water reaction with a base:
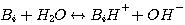
(3.20)
This reaction involves a proton transfer, therefore, the reactants and products of this reaction are always at local
equilibrium:
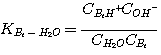
(3.21)
or:
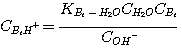
(3.22)
The amine can act as a base and reacts with water according to:

(3.23)
where:

(3.24)
Combining reactions 3.20 and 3.23 gives:
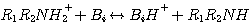
(3.25)
where:
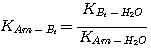
(3.26)
The reaction of amine with the zwitterion is given by:

(3.27)
Combining reactions 3.25 and 3.27 gives:
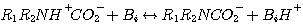
(3.28)
Comparing reactions 3.15 and 3.28 gives:
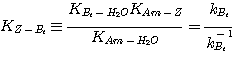
(3.29)
or:
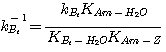
(3.30)
Adding reactions 3.14 and 3.15 and replacing with amine gives:

(3.31)
where:

(3.32)
or:

(3.33)
Substituting equations 3.24 and 3.33 into equation 3.30 gives:

(3.34)
Substituting equations 3.34 and 3.22 into equation 3.19 and rearranging gives:

(3.35)
The second term in the numerator of equation (3.35) represents the concentration of CO2 that is in is in
equilibrium with the amine, amine carbamate and protonated amine based on reaction 3.31. Hence, this equation can be
rewritten as:

(3.36)
As mentioned, the kinetics data for the CO2-MEA system follows a second order kinetics. Equation 3.35 is
reduced to
the second order form if the second term in the denominator is ignored in comparison to the first term, leading to:

(3.37)
The second order rate constant given by Hikita et al. 1977 will be used in this study to compute the CO2
absorption rate for systems containing MEA. This rate constant is expressed as a function of temperature by:
MEA:

(3.38)
In contrast, the first term in the denominator of equation (3.35) is negligible compared to the second term for the
CO2-DEA system:
DEA:

(3.39)
Equation 3.39 was used by Laddha and Danckwerts 1981, Blauwhoff et al. (1984), Versteeg and Van Swaaij (1988),
Critchfield (1988), and Glasscock (1990) to describe the kinetics data for the CO2-DEA system.
Glasscock (1990) assumed that the amine and the water are the only bases that contribute to the neutralization of the
zwitterion. The CO2-DEA rate expression reported by Glasscock 1990 will be utilized in this study.
This expression is given by
DEA:

(3.40)
The rate constants reported by Glasscock (1990) were extracted from the fit of the kinetics data and expressed as
functions of temperature according to

(3.41)

(3.42)
2.2 CO2 Reaction with MDEA
CO2 reacts indirectly with MDEA in the presence of water to form bicarbonate and protonated MDEA.
Three different mechanisms have been proposed for this reaction (Barth et al. 1981). The first mechanism suggests that
MDEA neutralizes the species formed by the CO2-water reactions (reactions 3.8 and 3.9). The second mechanism
assumes that MDEA associates with water before reacting with CO2:

(3.43)
The third mechanism follows the zwitterion mechanism described earlier for MEA and DEA:

(3.44)
The zwitterion formed immediately reacts with water and hydroxide to produce respectively bicarbonate and protonated
MDEA and bicarbonate and MDEA according to:
The third mechanism follows the zwitterion mechanism described earlier for MEA and DEA:

(3.45)

(3.46)
Adopting the third mechanism and following the procedure developed earlier for MEA and DEA, the following expression is
obtained for the rate of reaction of CO2 with MDEA:

(3.47)
Combining reactions 3.44 with 3.45 and 3.44 with 3.46 gives:

(3.48)

(3.49)
Reaction 3.48 can also be obtained from combinations of the following reactions:

(3.50)

(3.51)
Hence

(3.52)
Since reaction 3.50 is instantaneous, its products and reactants are at local equilibrium:

(3.53)
Therefore:

(3.54)
Reaction 3.49 can be obtained by combining the instantaneous water dissociation reaction (equation 2.1) with reaction
3.51 to obtain:

(3.55)
or:

(3.56)
Substituting equations 3.54 and 3.56 into equation 3.47 and rearranging gives:

(3.57)
or:

(3.58)
Similar to the derivation of MEA and DEA, the second term in the numerator of equation 3.58 represents the
concentration of CO2 which is in equilibrium with the bicarbonate and the hydroxide ions:

(3.59)
Equation 3.58 is a general rate expression for the reaction of CO2 with MDEA or any tertiary amine.
Depending on the magnitude of the second term of the denominator of this equation, one can obtain two limiting forms:

The rate expression in this case reduces to:

(3.60)
This form is essentially the expression, which would have been obtained if the second mechanism were used.
Many investigators including Haimor et al. (1987), Critchfield (1988), Tomcej et al. (1989), Little et al. (1990),
Rangwala et al. (1992), and Ko and Li (2000) adopted this form to fit the rate data of the CO2-MDEA system.
The rate constant of the reaction is given as a function of temperature by:

(3.61)
Comparison among the published values of the rate constant at 298.15 K shows a variation between 2.5 and 8.8
lit/mol/sec.

In this case the rate expression is given by:

(3.62)
Glasscock (1990) showed that this form reconciled the published rate data better.
He used activities instead of concentrations to obtain the rate constants. In the current study, the rate expression
represented by the first form (equation 3.60) with the rate constant reported by Critchfield (1988) will be used to model
the kinetics of the CO2 reaction with MDEA. The rate constant reported by Critchfield (1988) is given by:

(3.63)
2.3 CO2 Reaction with Blends of MEA-MDEA and DEA-MDEA
The absorption of CO2 in aqueous solution of blends of MEA-MDEA and DEA-MDEA was studied by Glasscock et
al. (1990), Versteeg et al. (1990), Rangwala et al. (1992), and Hagewiesche et al. (1995). Critchfield showed that the
interaction between MDEA and MEA is insignificant. Therefore the rate expressions (equation 3.37) for MEA and
(equation 3.60) for MDEA are still applicable for the mixture MEA-MDEA. However, for systems containing DEA and MDEA,
the latter acts as another base that neutralizes the zwitterion formed from the reaction of CO2 with DEA.
Hence, The CO2-DEA rate expression for systems containing DEA and MDEA should be corrected by adding the
contribution of MDEA to the neutralization of the zwitterion:
DEA/MDEA:

(3.64)

A value of 468 m6/kmol2/sec was reported in the thesis of Glasscock (1990) for the rate
constant k'R1R2R3N. In this work, this value will be used for
any temperature to compute the absorption rate of CO2in systems containing blends of DEA and MDEA.
Following the suggestion of Glasscock (1990), the effect of MDEA on the rate of reaction of CO2with MEA
will be ignored.
2. Mechanism of the CO2 Reaction in Aqueous Solutions of Alkanolamine
In any aqueous solution, CO2 reacts with water and hydroxide according
to the following reactions:
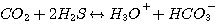
(3.8)
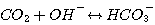
(3.9)
The CO2 consumption by reaction 3.8 is first order with respect
to CO2. The forward rate constant of
this reaction was correlated as a function of temperature by Pinsent and coworkers (Pinsent et al., 1956):
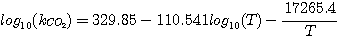
(3.10)
The rate of disappearance of CO2 by reaction 3.9 follows elementary
kinetics and can be expressed by:
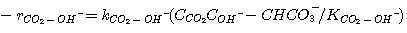
(3.11)
Astarita et al. (1983) studied the effect of ionic strength on the rate constant,
kCO2-OH-. They extended the expression originally presented by Sherwood et al.
(1975) to include the ionic strength:
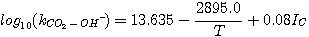
(3.12)
where IC is the concentration-based ionic strength given by:
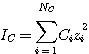
(3.13)
Reactions (3.8) and (3.9) are very slow compared to the CO2
reactions with MEA or DEA especially for
CO2 loadings less than 0.5. Ignoring these reactions does not affect the calculation of the rate of
absorption of CO2. Hence, the liquid film concentration of the bicarbonate ion is constant in systems
containing only MEA or DEA. On the other hand, MDEA is believed to catalyze these reactions. As a result, ignoring the
change of the liquid film concentration of the bicarbonate in systems containing MDEA might lead to an error in the
calculation of the CO2 absorption rate.
2.1 CO2 Reaction with MEA and DEA
The absorption of CO2 in aqueous solutions of
MEA and DEA has been extensively studied in the literature.
Several techniques have been used to collect the kinetics data. These include laminar jet falling film, rapid mixing,
falling film, diffusion across a porous media, and stirred reactor. Descriptions of the methodology and experimental set
up are given by Van Krevelen and Hoftijzer (1948), Nunge and Gill (1963), Coldrey and Harris (1976), Alvarez et al.
(1980), Glasscock (1990), Hogendoorn et al. (1993), and Ko and Li (2000).
The MEA reaction with CO2 has been studied
by several researchers including Astarita 1961, Leder 1971,
Sada et al. 1976, Hikita et al. 1977, Laddha and Danckwerts, 1981 and Blauwhoff et al. 1984. There is a general agreement
among the researchers that the reaction of CO2 with MEA follows a second order kinetics. The second order rate
constant of this reaction was correlated as a function of temperature by Hikita et al. 1977. The revision of the data made
by Blauwhoff et al. 1984 and Barth et al. 1986 supported the results of Hikita et al. 1977.
Blanc and Demarais (1984) revised the data and the
proposed mechanisms for the rate of reaction of CO2
with DEA. They realized that the researchers results vary significantly. The dependence of the reaction rate on the
concentration of DEA was reported as first or second order. The reported rate constants were also not comparable.
Blauwhoff et al. (1984) revised the reported kinetics data for this system. They concluded that the reaction rate of
CO2 with DEA is too complicated to be interpreted by a simple kinetic model. They further showed that the
zwitterion mechanism reconciles most of the CO2-DEA published kinetics data. The zwitterion mechanism was
adopted by Glasscock (1990) to represent the kinetics data of CO2 in primary and secondary alkanolamines.
This mechanism was originally proposed by Caplow in 1968 and introduced to the chemical engineering literature by
Danckwerts in 1979. According to this mechanism, CO2 reacts with MEA or DEA to form an unstable zwitterion, Z.
The zwitterion is instantaneously neutralized by any base, Bi, present in the solution to form the amine
carbamate and a protonated base, BiH+:
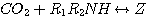
(3.14)

(3.15)
where Z ≡ R1R2NH+, R1 ≡ CH3CH2OH,
and R2 ≡ H and R1 for MEA and DEA, respectively. Reaction 3.14 is the rate controlling step;
hence the rate of disappearance of CO2 is given by:
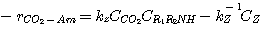
(3.16)
Since, the zwitterion is unstable, its rate of
formation is zero:

(3.17)
Solving for the concentration of the zwitterion
gives:
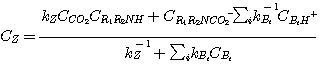
(3.18)
Substituting equation 3.18 into equation 3.16 and rearranging gives:

(3.19)
Equation 3.19 can be simplified by relating the groups of rate constants to their corresponding equilibrium
constants as follows. Consider the water reaction with a base:
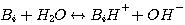
(3.20)
This reaction involves a proton transfer, therefore, the reactants and products of this reaction are always at local
equilibrium:
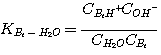
(3.21)
or:
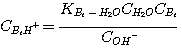
(3.22)
The amine can act as a base and reacts with water according to:

(3.23)
where:

(3.24)
Combining reactions 3.20 and 3.23 gives:
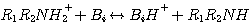
(3.25)
where:
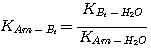
(3.26)
The reaction of amine with the zwitterion is given by:

(3.27)
Combining reactions 3.25 and 3.27 gives:
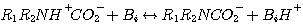
(3.28)
Comparing reactions 3.15 and 3.28 gives:
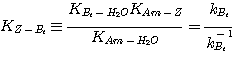
(3.29)
or:
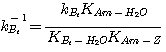
(3.30)
Adding reactions 3.14 and 3.15 and replacing with amine gives:

(3.31)
where:

(3.32)
or:

(3.33)
Substituting equations 3.24 and 3.33 into equation 3.30 gives:

(3.34)
Substituting equations 3.34 and 3.22 into equation 3.19 and rearranging gives:

(3.35)
The second term in the numerator of equation (3.35) represents the concentration of CO2 that is in is in
equilibrium with the amine, amine carbamate and protonated amine based on reaction 3.31. Hence, this equation can be
rewritten as:

(3.36)
As mentioned, the kinetics data for the CO2-MEA system follows a second order kinetics. Equation 3.35 is
reduced to
the second order form if the second term in the denominator is ignored in comparison to the first term, leading to:

(3.37)
The second order rate constant given by Hikita et al. 1977 will be used in this study to compute the CO2
absorption rate for systems containing MEA. This rate constant is expressed as a function of temperature by:
MEA:

(3.38)
In contrast, the first term in the denominator of equation (3.35) is negligible compared to the second term for the
CO2-DEA system:
DEA:

(3.39)
Equation 3.39 was used by Laddha and Danckwerts 1981, Blauwhoff et al. (1984), Versteeg and Van Swaaij (1988),
Critchfield (1988), and Glasscock (1990) to describe the kinetics data for the CO2-DEA system.
Glasscock (1990) assumed that the amine and the water are the only bases that contribute to the neutralization of the
zwitterion. The CO2-DEA rate expression reported by Glasscock 1990 will be utilized in this study.
This expression is given by
DEA:

(3.40)
The rate constants reported by Glasscock (1990) were extracted from the fit of the kinetics data and expressed as
functions of temperature according to

(3.41)

(3.42)
2.2 CO2 Reaction with MDEA
CO2 reacts indirectly with MDEA in the presence of water to form bicarbonate and protonated MDEA.
Three different mechanisms have been proposed for this reaction (Barth et al. 1981). The first mechanism suggests that
MDEA neutralizes the species formed by the CO2-water reactions (reactions 3.8 and 3.9). The second mechanism
assumes that MDEA associates with water before reacting with CO2:

(3.43)
The third mechanism follows the zwitterion mechanism described earlier for MEA and DEA:

(3.44)
The zwitterion formed immediately reacts with water and hydroxide to produce respectively bicarbonate and protonated
MDEA and bicarbonate and MDEA according to:
The third mechanism follows the zwitterion mechanism described earlier for MEA and DEA:

(3.45)

(3.46)
Adopting the third mechanism and following the procedure developed earlier for MEA and DEA, the following expression is
obtained for the rate of reaction of CO2 with MDEA:

(3.47)
Combining reactions 3.44 with 3.45 and 3.44 with 3.46 gives:

(3.48)

(3.49)
Reaction 3.48 can also be obtained from combinations of the following reactions:

(3.50)

(3.51)
Hence

(3.52)
Since reaction 3.50 is instantaneous, its products and reactants are at local equilibrium:

(3.53)
Therefore:

(3.54)
Reaction 3.49 can be obtained by combining the instantaneous water dissociation reaction (equation 2.1) with reaction
3.51 to obtain:

(3.55)
or:

(3.56)
Substituting equations 3.54 and 3.56 into equation 3.47 and rearranging gives:

(3.57)
or:

(3.58)
Similar to the derivation of MEA and DEA, the second term in the numerator of equation 3.58 represents the
concentration of CO2 which is in equilibrium with the bicarbonate and the hydroxide ions:

(3.59)
Equation 3.58 is a general rate expression for the reaction of CO2 with MDEA or any tertiary amine.
Depending on the magnitude of the second term of the denominator of this equation, one can obtain two limiting forms:

The rate expression in this case reduces to:

(3.60)
This form is essentially the expression, which would have been obtained if the second mechanism were used.
Many investigators including Haimor et al. (1987), Critchfield (1988), Tomcej et al. (1989), Little et al. (1990),
Rangwala et al. (1992), and Ko and Li (2000) adopted this form to fit the rate data of the CO2-MDEA system.
The rate constant of the reaction is given as a function of temperature by:

(3.61)
Comparison among the published values of the rate constant at 298.15 K shows a variation between 2.5 and 8.8
lit/mol/sec.

In this case the rate expression is given by:

(3.62)
Glasscock (1990) showed that this form reconciled the published rate data better.
He used activities instead of concentrations to obtain the rate constants. In the current study, the rate expression
represented by the first form (equation 3.60) with the rate constant reported by Critchfield (1988) will be used to model
the kinetics of the CO2 reaction with MDEA. The rate constant reported by Critchfield (1988) is given by:

(3.63)
2.3 CO2 Reaction with Blends of MEA-MDEA and DEA-MDEA
The absorption of CO2 in aqueous solution of blends of MEA-MDEA and DEA-MDEA was studied by Glasscock et
al. (1990), Versteeg et al. (1990), Rangwala et al. (1992), and Hagewiesche et al. (1995). Critchfield showed that the
interaction between MDEA and MEA is insignificant. Therefore the rate expressions (equation 3.37) for MEA and
(equation 3.60) for MDEA are still applicable for the mixture MEA-MDEA. However, for systems containing DEA and MDEA,
the latter acts as another base that neutralizes the zwitterion formed from the reaction of CO2 with DEA.
Hence, The CO2-DEA rate expression for systems containing DEA and MDEA should be corrected by adding the
contribution of MDEA to the neutralization of the zwitterion:
DEA/MDEA:

(3.64)

A value of 468 m6/kmol2/sec was reported in the thesis of Glasscock (1990) for the rate
constant k'R1R2R3N. In this work, this value will be used for
any temperature to compute the absorption rate of CO2in systems containing blends of DEA and MDEA.
Following the suggestion of Glasscock (1990), the effect of MDEA on the rate of reaction of CO2with MEA
will be ignored.
|
|
(3.8) |
|
|
(3.9) |
The CO2 consumption by reaction 3.8 is first order with respect
to CO2. The forward rate constant of
this reaction was correlated as a function of temperature by Pinsent and coworkers (Pinsent et al., 1956):
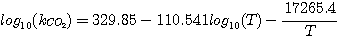
(3.10)
The rate of disappearance of CO2 by reaction 3.9 follows elementary
kinetics and can be expressed by:
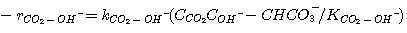
(3.11)
Astarita et al. (1983) studied the effect of ionic strength on the rate constant,
kCO2-OH-. They extended the expression originally presented by Sherwood et al.
(1975) to include the ionic strength:
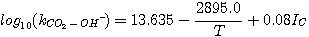
(3.12)
where IC is the concentration-based ionic strength given by:
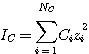
(3.13)
Reactions (3.8) and (3.9) are very slow compared to the CO2
reactions with MEA or DEA especially for
CO2 loadings less than 0.5. Ignoring these reactions does not affect the calculation of the rate of
absorption of CO2. Hence, the liquid film concentration of the bicarbonate ion is constant in systems
containing only MEA or DEA. On the other hand, MDEA is believed to catalyze these reactions. As a result, ignoring the
change of the liquid film concentration of the bicarbonate in systems containing MDEA might lead to an error in the
calculation of the CO2 absorption rate.
2.1 CO2 Reaction with MEA and DEA
The absorption of CO2 in aqueous solutions of
MEA and DEA has been extensively studied in the literature.
Several techniques have been used to collect the kinetics data. These include laminar jet falling film, rapid mixing,
falling film, diffusion across a porous media, and stirred reactor. Descriptions of the methodology and experimental set
up are given by Van Krevelen and Hoftijzer (1948), Nunge and Gill (1963), Coldrey and Harris (1976), Alvarez et al.
(1980), Glasscock (1990), Hogendoorn et al. (1993), and Ko and Li (2000).
The MEA reaction with CO2 has been studied
by several researchers including Astarita 1961, Leder 1971,
Sada et al. 1976, Hikita et al. 1977, Laddha and Danckwerts, 1981 and Blauwhoff et al. 1984. There is a general agreement
among the researchers that the reaction of CO2 with MEA follows a second order kinetics. The second order rate
constant of this reaction was correlated as a function of temperature by Hikita et al. 1977. The revision of the data made
by Blauwhoff et al. 1984 and Barth et al. 1986 supported the results of Hikita et al. 1977.
Blanc and Demarais (1984) revised the data and the
proposed mechanisms for the rate of reaction of CO2
with DEA. They realized that the researchers results vary significantly. The dependence of the reaction rate on the
concentration of DEA was reported as first or second order. The reported rate constants were also not comparable.
Blauwhoff et al. (1984) revised the reported kinetics data for this system. They concluded that the reaction rate of
CO2 with DEA is too complicated to be interpreted by a simple kinetic model. They further showed that the
zwitterion mechanism reconciles most of the CO2-DEA published kinetics data. The zwitterion mechanism was
adopted by Glasscock (1990) to represent the kinetics data of CO2 in primary and secondary alkanolamines.
This mechanism was originally proposed by Caplow in 1968 and introduced to the chemical engineering literature by
Danckwerts in 1979. According to this mechanism, CO2 reacts with MEA or DEA to form an unstable zwitterion, Z.
The zwitterion is instantaneously neutralized by any base, Bi, present in the solution to form the amine
carbamate and a protonated base, BiH+:
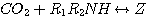
(3.14)

(3.15)
where Z ≡ R1R2NH+, R1 ≡ CH3CH2OH,
and R2 ≡ H and R1 for MEA and DEA, respectively. Reaction 3.14 is the rate controlling step;
hence the rate of disappearance of CO2 is given by:
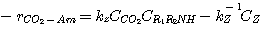
(3.16)
Since, the zwitterion is unstable, its rate of
formation is zero:

(3.17)
Solving for the concentration of the zwitterion
gives:
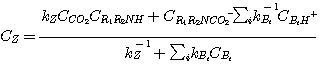
(3.18)
Substituting equation 3.18 into equation 3.16 and rearranging gives:

(3.19)
Equation 3.19 can be simplified by relating the groups of rate constants to their corresponding equilibrium
constants as follows. Consider the water reaction with a base:
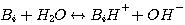
(3.20)
This reaction involves a proton transfer, therefore, the reactants and products of this reaction are always at local
equilibrium:
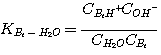
(3.21)
or:
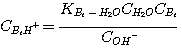
(3.22)
The amine can act as a base and reacts with water according to:

(3.23)
where:

(3.24)
Combining reactions 3.20 and 3.23 gives:
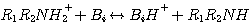
(3.25)
where:
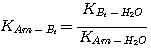
(3.26)
The reaction of amine with the zwitterion is given by:

(3.27)
Combining reactions 3.25 and 3.27 gives:
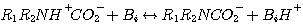
(3.28)
Comparing reactions 3.15 and 3.28 gives:
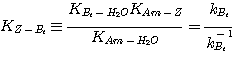
(3.29)
or:
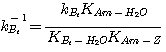
(3.30)
Adding reactions 3.14 and 3.15 and replacing with amine gives:

(3.31)
where:

(3.32)
or:

(3.33)
Substituting equations 3.24 and 3.33 into equation 3.30 gives:

(3.34)
Substituting equations 3.34 and 3.22 into equation 3.19 and rearranging gives:

(3.35)
The second term in the numerator of equation (3.35) represents the concentration of CO2 that is in is in
equilibrium with the amine, amine carbamate and protonated amine based on reaction 3.31. Hence, this equation can be
rewritten as:

(3.36)
As mentioned, the kinetics data for the CO2-MEA system follows a second order kinetics. Equation 3.35 is
reduced to
the second order form if the second term in the denominator is ignored in comparison to the first term, leading to:

(3.37)
The second order rate constant given by Hikita et al. 1977 will be used in this study to compute the CO2
absorption rate for systems containing MEA. This rate constant is expressed as a function of temperature by:
MEA:

(3.38)
In contrast, the first term in the denominator of equation (3.35) is negligible compared to the second term for the
CO2-DEA system:
DEA:

(3.39)
Equation 3.39 was used by Laddha and Danckwerts 1981, Blauwhoff et al. (1984), Versteeg and Van Swaaij (1988),
Critchfield (1988), and Glasscock (1990) to describe the kinetics data for the CO2-DEA system.
Glasscock (1990) assumed that the amine and the water are the only bases that contribute to the neutralization of the
zwitterion. The CO2-DEA rate expression reported by Glasscock 1990 will be utilized in this study.
This expression is given by
DEA:

(3.40)
The rate constants reported by Glasscock (1990) were extracted from the fit of the kinetics data and expressed as
functions of temperature according to

(3.41)

(3.42)
2.2 CO2 Reaction with MDEA
CO2 reacts indirectly with MDEA in the presence of water to form bicarbonate and protonated MDEA.
Three different mechanisms have been proposed for this reaction (Barth et al. 1981). The first mechanism suggests that
MDEA neutralizes the species formed by the CO2-water reactions (reactions 3.8 and 3.9). The second mechanism
assumes that MDEA associates with water before reacting with CO2:

(3.43)
The third mechanism follows the zwitterion mechanism described earlier for MEA and DEA:

(3.44)
The zwitterion formed immediately reacts with water and hydroxide to produce respectively bicarbonate and protonated
MDEA and bicarbonate and MDEA according to:
The third mechanism follows the zwitterion mechanism described earlier for MEA and DEA:

(3.45)

(3.46)
Adopting the third mechanism and following the procedure developed earlier for MEA and DEA, the following expression is
obtained for the rate of reaction of CO2 with MDEA:

(3.47)
Combining reactions 3.44 with 3.45 and 3.44 with 3.46 gives:

(3.48)

(3.49)
Reaction 3.48 can also be obtained from combinations of the following reactions:

(3.50)

(3.51)
Hence

(3.52)
Since reaction 3.50 is instantaneous, its products and reactants are at local equilibrium:

(3.53)
Therefore:

(3.54)
Reaction 3.49 can be obtained by combining the instantaneous water dissociation reaction (equation 2.1) with reaction
3.51 to obtain:

(3.55)
or:

(3.56)
Substituting equations 3.54 and 3.56 into equation 3.47 and rearranging gives:

(3.57)
or:

(3.58)
Similar to the derivation of MEA and DEA, the second term in the numerator of equation 3.58 represents the
concentration of CO2 which is in equilibrium with the bicarbonate and the hydroxide ions:

(3.59)
Equation 3.58 is a general rate expression for the reaction of CO2 with MDEA or any tertiary amine.
Depending on the magnitude of the second term of the denominator of this equation, one can obtain two limiting forms:

The rate expression in this case reduces to:

(3.60)
This form is essentially the expression, which would have been obtained if the second mechanism were used.
Many investigators including Haimor et al. (1987), Critchfield (1988), Tomcej et al. (1989), Little et al. (1990),
Rangwala et al. (1992), and Ko and Li (2000) adopted this form to fit the rate data of the CO2-MDEA system.
The rate constant of the reaction is given as a function of temperature by:

(3.61)
Comparison among the published values of the rate constant at 298.15 K shows a variation between 2.5 and 8.8
lit/mol/sec.

In this case the rate expression is given by:

(3.62)
Glasscock (1990) showed that this form reconciled the published rate data better.
He used activities instead of concentrations to obtain the rate constants. In the current study, the rate expression
represented by the first form (equation 3.60) with the rate constant reported by Critchfield (1988) will be used to model
the kinetics of the CO2 reaction with MDEA. The rate constant reported by Critchfield (1988) is given by:

(3.63)
2.3 CO2 Reaction with Blends of MEA-MDEA and DEA-MDEA
The absorption of CO2 in aqueous solution of blends of MEA-MDEA and DEA-MDEA was studied by Glasscock et
al. (1990), Versteeg et al. (1990), Rangwala et al. (1992), and Hagewiesche et al. (1995). Critchfield showed that the
interaction between MDEA and MEA is insignificant. Therefore the rate expressions (equation 3.37) for MEA and
(equation 3.60) for MDEA are still applicable for the mixture MEA-MDEA. However, for systems containing DEA and MDEA,
the latter acts as another base that neutralizes the zwitterion formed from the reaction of CO2 with DEA.
Hence, The CO2-DEA rate expression for systems containing DEA and MDEA should be corrected by adding the
contribution of MDEA to the neutralization of the zwitterion:
DEA/MDEA:

(3.64)

A value of 468 m6/kmol2/sec was reported in the thesis of Glasscock (1990) for the rate
constant k'R1R2R3N. In this work, this value will be used for
any temperature to compute the absorption rate of CO2in systems containing blends of DEA and MDEA.
Following the suggestion of Glasscock (1990), the effect of MDEA on the rate of reaction of CO2with MEA
will be ignored.
|
|
(3.10) |
The rate of disappearance of CO2 by reaction 3.9 follows elementary
kinetics and can be expressed by:
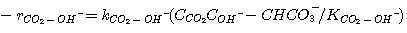
(3.11)
Astarita et al. (1983) studied the effect of ionic strength on the rate constant,
kCO2-OH-. They extended the expression originally presented by Sherwood et al.
(1975) to include the ionic strength:
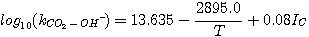
(3.12)
where IC is the concentration-based ionic strength given by:
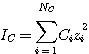
(3.13)
Reactions (3.8) and (3.9) are very slow compared to the CO2
reactions with MEA or DEA especially for
CO2 loadings less than 0.5. Ignoring these reactions does not affect the calculation of the rate of
absorption of CO2. Hence, the liquid film concentration of the bicarbonate ion is constant in systems
containing only MEA or DEA. On the other hand, MDEA is believed to catalyze these reactions. As a result, ignoring the
change of the liquid film concentration of the bicarbonate in systems containing MDEA might lead to an error in the
calculation of the CO2 absorption rate.
2.1 CO2 Reaction with MEA and DEA
The absorption of CO2 in aqueous solutions of
MEA and DEA has been extensively studied in the literature.
Several techniques have been used to collect the kinetics data. These include laminar jet falling film, rapid mixing,
falling film, diffusion across a porous media, and stirred reactor. Descriptions of the methodology and experimental set
up are given by Van Krevelen and Hoftijzer (1948), Nunge and Gill (1963), Coldrey and Harris (1976), Alvarez et al.
(1980), Glasscock (1990), Hogendoorn et al. (1993), and Ko and Li (2000).
The MEA reaction with CO2 has been studied
by several researchers including Astarita 1961, Leder 1971,
Sada et al. 1976, Hikita et al. 1977, Laddha and Danckwerts, 1981 and Blauwhoff et al. 1984. There is a general agreement
among the researchers that the reaction of CO2 with MEA follows a second order kinetics. The second order rate
constant of this reaction was correlated as a function of temperature by Hikita et al. 1977. The revision of the data made
by Blauwhoff et al. 1984 and Barth et al. 1986 supported the results of Hikita et al. 1977.
Blanc and Demarais (1984) revised the data and the
proposed mechanisms for the rate of reaction of CO2
with DEA. They realized that the researchers results vary significantly. The dependence of the reaction rate on the
concentration of DEA was reported as first or second order. The reported rate constants were also not comparable.
Blauwhoff et al. (1984) revised the reported kinetics data for this system. They concluded that the reaction rate of
CO2 with DEA is too complicated to be interpreted by a simple kinetic model. They further showed that the
zwitterion mechanism reconciles most of the CO2-DEA published kinetics data. The zwitterion mechanism was
adopted by Glasscock (1990) to represent the kinetics data of CO2 in primary and secondary alkanolamines.
This mechanism was originally proposed by Caplow in 1968 and introduced to the chemical engineering literature by
Danckwerts in 1979. According to this mechanism, CO2 reacts with MEA or DEA to form an unstable zwitterion, Z.
The zwitterion is instantaneously neutralized by any base, Bi, present in the solution to form the amine
carbamate and a protonated base, BiH+:
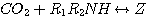
(3.14)

(3.15)
where Z ≡ R1R2NH+, R1 ≡ CH3CH2OH,
and R2 ≡ H and R1 for MEA and DEA, respectively. Reaction 3.14 is the rate controlling step;
hence the rate of disappearance of CO2 is given by:
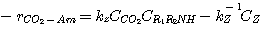
(3.16)
Since, the zwitterion is unstable, its rate of
formation is zero:

(3.17)
Solving for the concentration of the zwitterion
gives:
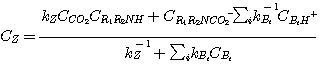
(3.18)
Substituting equation 3.18 into equation 3.16 and rearranging gives:

(3.19)
Equation 3.19 can be simplified by relating the groups of rate constants to their corresponding equilibrium
constants as follows. Consider the water reaction with a base:
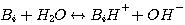
(3.20)
This reaction involves a proton transfer, therefore, the reactants and products of this reaction are always at local
equilibrium:
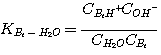
(3.21)
or:
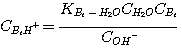
(3.22)
The amine can act as a base and reacts with water according to:

(3.23)
where:

(3.24)
Combining reactions 3.20 and 3.23 gives:
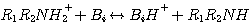
(3.25)
where:
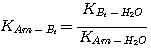
(3.26)
The reaction of amine with the zwitterion is given by:

(3.27)
Combining reactions 3.25 and 3.27 gives:
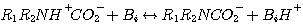
(3.28)
Comparing reactions 3.15 and 3.28 gives:
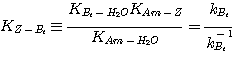
(3.29)
or:
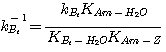
(3.30)
Adding reactions 3.14 and 3.15 and replacing with amine gives:

(3.31)
where:

(3.32)
or:

(3.33)
Substituting equations 3.24 and 3.33 into equation 3.30 gives:

(3.34)
Substituting equations 3.34 and 3.22 into equation 3.19 and rearranging gives:

(3.35)
The second term in the numerator of equation (3.35) represents the concentration of CO2 that is in is in
equilibrium with the amine, amine carbamate and protonated amine based on reaction 3.31. Hence, this equation can be
rewritten as:

(3.36)
As mentioned, the kinetics data for the CO2-MEA system follows a second order kinetics. Equation 3.35 is
reduced to
the second order form if the second term in the denominator is ignored in comparison to the first term, leading to:

(3.37)
The second order rate constant given by Hikita et al. 1977 will be used in this study to compute the CO2
absorption rate for systems containing MEA. This rate constant is expressed as a function of temperature by:
MEA:

(3.38)
In contrast, the first term in the denominator of equation (3.35) is negligible compared to the second term for the
CO2-DEA system:
DEA:

(3.39)
Equation 3.39 was used by Laddha and Danckwerts 1981, Blauwhoff et al. (1984), Versteeg and Van Swaaij (1988),
Critchfield (1988), and Glasscock (1990) to describe the kinetics data for the CO2-DEA system.
Glasscock (1990) assumed that the amine and the water are the only bases that contribute to the neutralization of the
zwitterion. The CO2-DEA rate expression reported by Glasscock 1990 will be utilized in this study.
This expression is given by
DEA:

(3.40)
The rate constants reported by Glasscock (1990) were extracted from the fit of the kinetics data and expressed as
functions of temperature according to

(3.41)

(3.42)
2.2 CO2 Reaction with MDEA
CO2 reacts indirectly with MDEA in the presence of water to form bicarbonate and protonated MDEA.
Three different mechanisms have been proposed for this reaction (Barth et al. 1981). The first mechanism suggests that
MDEA neutralizes the species formed by the CO2-water reactions (reactions 3.8 and 3.9). The second mechanism
assumes that MDEA associates with water before reacting with CO2:

(3.43)
The third mechanism follows the zwitterion mechanism described earlier for MEA and DEA:

(3.44)
The zwitterion formed immediately reacts with water and hydroxide to produce respectively bicarbonate and protonated
MDEA and bicarbonate and MDEA according to:
The third mechanism follows the zwitterion mechanism described earlier for MEA and DEA:

(3.45)

(3.46)
Adopting the third mechanism and following the procedure developed earlier for MEA and DEA, the following expression is
obtained for the rate of reaction of CO2 with MDEA:

(3.47)
Combining reactions 3.44 with 3.45 and 3.44 with 3.46 gives:

(3.48)

(3.49)
Reaction 3.48 can also be obtained from combinations of the following reactions:

(3.50)

(3.51)
Hence

(3.52)
Since reaction 3.50 is instantaneous, its products and reactants are at local equilibrium:

(3.53)
Therefore:

(3.54)
Reaction 3.49 can be obtained by combining the instantaneous water dissociation reaction (equation 2.1) with reaction
3.51 to obtain:

(3.55)
or:

(3.56)
Substituting equations 3.54 and 3.56 into equation 3.47 and rearranging gives:

(3.57)
or:

(3.58)
Similar to the derivation of MEA and DEA, the second term in the numerator of equation 3.58 represents the
concentration of CO2 which is in equilibrium with the bicarbonate and the hydroxide ions:

(3.59)
Equation 3.58 is a general rate expression for the reaction of CO2 with MDEA or any tertiary amine.
Depending on the magnitude of the second term of the denominator of this equation, one can obtain two limiting forms:

The rate expression in this case reduces to:

(3.60)
This form is essentially the expression, which would have been obtained if the second mechanism were used.
Many investigators including Haimor et al. (1987), Critchfield (1988), Tomcej et al. (1989), Little et al. (1990),
Rangwala et al. (1992), and Ko and Li (2000) adopted this form to fit the rate data of the CO2-MDEA system.
The rate constant of the reaction is given as a function of temperature by:

(3.61)
Comparison among the published values of the rate constant at 298.15 K shows a variation between 2.5 and 8.8
lit/mol/sec.

In this case the rate expression is given by:

(3.62)
Glasscock (1990) showed that this form reconciled the published rate data better.
He used activities instead of concentrations to obtain the rate constants. In the current study, the rate expression
represented by the first form (equation 3.60) with the rate constant reported by Critchfield (1988) will be used to model
the kinetics of the CO2 reaction with MDEA. The rate constant reported by Critchfield (1988) is given by:

(3.63)
2.3 CO2 Reaction with Blends of MEA-MDEA and DEA-MDEA
The absorption of CO2 in aqueous solution of blends of MEA-MDEA and DEA-MDEA was studied by Glasscock et
al. (1990), Versteeg et al. (1990), Rangwala et al. (1992), and Hagewiesche et al. (1995). Critchfield showed that the
interaction between MDEA and MEA is insignificant. Therefore the rate expressions (equation 3.37) for MEA and
(equation 3.60) for MDEA are still applicable for the mixture MEA-MDEA. However, for systems containing DEA and MDEA,
the latter acts as another base that neutralizes the zwitterion formed from the reaction of CO2 with DEA.
Hence, The CO2-DEA rate expression for systems containing DEA and MDEA should be corrected by adding the
contribution of MDEA to the neutralization of the zwitterion:
DEA/MDEA:

(3.64)

A value of 468 m6/kmol2/sec was reported in the thesis of Glasscock (1990) for the rate
constant k'R1R2R3N. In this work, this value will be used for
any temperature to compute the absorption rate of CO2in systems containing blends of DEA and MDEA.
Following the suggestion of Glasscock (1990), the effect of MDEA on the rate of reaction of CO2with MEA
will be ignored.
|
|
(3.11) |
Astarita et al. (1983) studied the effect of ionic strength on the rate constant,
kCO2-OH-. They extended the expression originally presented by Sherwood et al.
(1975) to include the ionic strength:
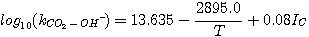
(3.12)
where IC is the concentration-based ionic strength given by:
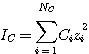
(3.13)
Reactions (3.8) and (3.9) are very slow compared to the CO2
reactions with MEA or DEA especially for
CO2 loadings less than 0.5. Ignoring these reactions does not affect the calculation of the rate of
absorption of CO2. Hence, the liquid film concentration of the bicarbonate ion is constant in systems
containing only MEA or DEA. On the other hand, MDEA is believed to catalyze these reactions. As a result, ignoring the
change of the liquid film concentration of the bicarbonate in systems containing MDEA might lead to an error in the
calculation of the CO2 absorption rate.
2.1 CO2 Reaction with MEA and DEA
The absorption of CO2 in aqueous solutions of
MEA and DEA has been extensively studied in the literature.
Several techniques have been used to collect the kinetics data. These include laminar jet falling film, rapid mixing,
falling film, diffusion across a porous media, and stirred reactor. Descriptions of the methodology and experimental set
up are given by Van Krevelen and Hoftijzer (1948), Nunge and Gill (1963), Coldrey and Harris (1976), Alvarez et al.
(1980), Glasscock (1990), Hogendoorn et al. (1993), and Ko and Li (2000).
The MEA reaction with CO2 has been studied
by several researchers including Astarita 1961, Leder 1971,
Sada et al. 1976, Hikita et al. 1977, Laddha and Danckwerts, 1981 and Blauwhoff et al. 1984. There is a general agreement
among the researchers that the reaction of CO2 with MEA follows a second order kinetics. The second order rate
constant of this reaction was correlated as a function of temperature by Hikita et al. 1977. The revision of the data made
by Blauwhoff et al. 1984 and Barth et al. 1986 supported the results of Hikita et al. 1977.
Blanc and Demarais (1984) revised the data and the
proposed mechanisms for the rate of reaction of CO2
with DEA. They realized that the researchers results vary significantly. The dependence of the reaction rate on the
concentration of DEA was reported as first or second order. The reported rate constants were also not comparable.
Blauwhoff et al. (1984) revised the reported kinetics data for this system. They concluded that the reaction rate of
CO2 with DEA is too complicated to be interpreted by a simple kinetic model. They further showed that the
zwitterion mechanism reconciles most of the CO2-DEA published kinetics data. The zwitterion mechanism was
adopted by Glasscock (1990) to represent the kinetics data of CO2 in primary and secondary alkanolamines.
This mechanism was originally proposed by Caplow in 1968 and introduced to the chemical engineering literature by
Danckwerts in 1979. According to this mechanism, CO2 reacts with MEA or DEA to form an unstable zwitterion, Z.
The zwitterion is instantaneously neutralized by any base, Bi, present in the solution to form the amine
carbamate and a protonated base, BiH+:
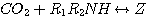
(3.14)

(3.15)
where Z ≡ R1R2NH+, R1 ≡ CH3CH2OH,
and R2 ≡ H and R1 for MEA and DEA, respectively. Reaction 3.14 is the rate controlling step;
hence the rate of disappearance of CO2 is given by:
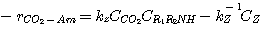
(3.16)
Since, the zwitterion is unstable, its rate of
formation is zero:

(3.17)
Solving for the concentration of the zwitterion
gives:
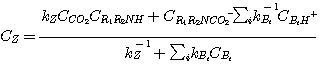
(3.18)
Substituting equation 3.18 into equation 3.16 and rearranging gives:

(3.19)
Equation 3.19 can be simplified by relating the groups of rate constants to their corresponding equilibrium
constants as follows. Consider the water reaction with a base:
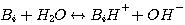
(3.20)
This reaction involves a proton transfer, therefore, the reactants and products of this reaction are always at local
equilibrium:
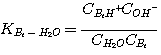
(3.21)
or:
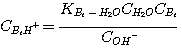
(3.22)
The amine can act as a base and reacts with water according to:

(3.23)
where:

(3.24)
Combining reactions 3.20 and 3.23 gives:
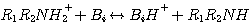
(3.25)
where:
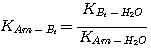
(3.26)
The reaction of amine with the zwitterion is given by:

(3.27)
Combining reactions 3.25 and 3.27 gives:
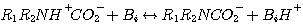
(3.28)
Comparing reactions 3.15 and 3.28 gives:
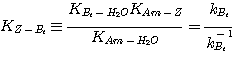
(3.29)
or:
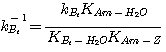
(3.30)
Adding reactions 3.14 and 3.15 and replacing with amine gives:

(3.31)
where:

(3.32)
or:

(3.33)
Substituting equations 3.24 and 3.33 into equation 3.30 gives:

(3.34)
Substituting equations 3.34 and 3.22 into equation 3.19 and rearranging gives:

(3.35)
The second term in the numerator of equation (3.35) represents the concentration of CO2 that is in is in
equilibrium with the amine, amine carbamate and protonated amine based on reaction 3.31. Hence, this equation can be
rewritten as:

(3.36)
As mentioned, the kinetics data for the CO2-MEA system follows a second order kinetics. Equation 3.35 is
reduced to
the second order form if the second term in the denominator is ignored in comparison to the first term, leading to:

(3.37)
The second order rate constant given by Hikita et al. 1977 will be used in this study to compute the CO2
absorption rate for systems containing MEA. This rate constant is expressed as a function of temperature by:
MEA:

(3.38)
In contrast, the first term in the denominator of equation (3.35) is negligible compared to the second term for the
CO2-DEA system:
DEA:

(3.39)
Equation 3.39 was used by Laddha and Danckwerts 1981, Blauwhoff et al. (1984), Versteeg and Van Swaaij (1988),
Critchfield (1988), and Glasscock (1990) to describe the kinetics data for the CO2-DEA system.
Glasscock (1990) assumed that the amine and the water are the only bases that contribute to the neutralization of the
zwitterion. The CO2-DEA rate expression reported by Glasscock 1990 will be utilized in this study.
This expression is given by
DEA:

(3.40)
The rate constants reported by Glasscock (1990) were extracted from the fit of the kinetics data and expressed as
functions of temperature according to

(3.41)

(3.42)
2.2 CO2 Reaction with MDEA
CO2 reacts indirectly with MDEA in the presence of water to form bicarbonate and protonated MDEA.
Three different mechanisms have been proposed for this reaction (Barth et al. 1981). The first mechanism suggests that
MDEA neutralizes the species formed by the CO2-water reactions (reactions 3.8 and 3.9). The second mechanism
assumes that MDEA associates with water before reacting with CO2:

(3.43)
The third mechanism follows the zwitterion mechanism described earlier for MEA and DEA:

(3.44)
The zwitterion formed immediately reacts with water and hydroxide to produce respectively bicarbonate and protonated
MDEA and bicarbonate and MDEA according to:
The third mechanism follows the zwitterion mechanism described earlier for MEA and DEA:

(3.45)

(3.46)
Adopting the third mechanism and following the procedure developed earlier for MEA and DEA, the following expression is
obtained for the rate of reaction of CO2 with MDEA:

(3.47)
Combining reactions 3.44 with 3.45 and 3.44 with 3.46 gives:

(3.48)

(3.49)
Reaction 3.48 can also be obtained from combinations of the following reactions:

(3.50)

(3.51)
Hence

(3.52)
Since reaction 3.50 is instantaneous, its products and reactants are at local equilibrium:

(3.53)
Therefore:

(3.54)
Reaction 3.49 can be obtained by combining the instantaneous water dissociation reaction (equation 2.1) with reaction
3.51 to obtain:

(3.55)
or:

(3.56)
Substituting equations 3.54 and 3.56 into equation 3.47 and rearranging gives:

(3.57)
or:

(3.58)
Similar to the derivation of MEA and DEA, the second term in the numerator of equation 3.58 represents the
concentration of CO2 which is in equilibrium with the bicarbonate and the hydroxide ions:

(3.59)
Equation 3.58 is a general rate expression for the reaction of CO2 with MDEA or any tertiary amine.
Depending on the magnitude of the second term of the denominator of this equation, one can obtain two limiting forms:

The rate expression in this case reduces to:

(3.60)
This form is essentially the expression, which would have been obtained if the second mechanism were used.
Many investigators including Haimor et al. (1987), Critchfield (1988), Tomcej et al. (1989), Little et al. (1990),
Rangwala et al. (1992), and Ko and Li (2000) adopted this form to fit the rate data of the CO2-MDEA system.
The rate constant of the reaction is given as a function of temperature by:

(3.61)
Comparison among the published values of the rate constant at 298.15 K shows a variation between 2.5 and 8.8
lit/mol/sec.

In this case the rate expression is given by:

(3.62)
Glasscock (1990) showed that this form reconciled the published rate data better.
He used activities instead of concentrations to obtain the rate constants. In the current study, the rate expression
represented by the first form (equation 3.60) with the rate constant reported by Critchfield (1988) will be used to model
the kinetics of the CO2 reaction with MDEA. The rate constant reported by Critchfield (1988) is given by:

(3.63)
2.3 CO2 Reaction with Blends of MEA-MDEA and DEA-MDEA
The absorption of CO2 in aqueous solution of blends of MEA-MDEA and DEA-MDEA was studied by Glasscock et
al. (1990), Versteeg et al. (1990), Rangwala et al. (1992), and Hagewiesche et al. (1995). Critchfield showed that the
interaction between MDEA and MEA is insignificant. Therefore the rate expressions (equation 3.37) for MEA and
(equation 3.60) for MDEA are still applicable for the mixture MEA-MDEA. However, for systems containing DEA and MDEA,
the latter acts as another base that neutralizes the zwitterion formed from the reaction of CO2 with DEA.
Hence, The CO2-DEA rate expression for systems containing DEA and MDEA should be corrected by adding the
contribution of MDEA to the neutralization of the zwitterion:
DEA/MDEA:

(3.64)

A value of 468 m6/kmol2/sec was reported in the thesis of Glasscock (1990) for the rate
constant k'R1R2R3N. In this work, this value will be used for
any temperature to compute the absorption rate of CO2in systems containing blends of DEA and MDEA.
Following the suggestion of Glasscock (1990), the effect of MDEA on the rate of reaction of CO2with MEA
will be ignored.
|
|
(3.12) |
where IC is the concentration-based ionic strength given by:
|
|
(3.13) |
Reactions (3.8) and (3.9) are very slow compared to the CO2
reactions with MEA or DEA especially for
CO2 loadings less than 0.5. Ignoring these reactions does not affect the calculation of the rate of
absorption of CO2. Hence, the liquid film concentration of the bicarbonate ion is constant in systems
containing only MEA or DEA. On the other hand, MDEA is believed to catalyze these reactions. As a result, ignoring the
change of the liquid film concentration of the bicarbonate in systems containing MDEA might lead to an error in the
calculation of the CO2 absorption rate.
2.1 CO2 Reaction with MEA and DEA
The absorption of CO2 in aqueous solutions of
MEA and DEA has been extensively studied in the literature.
Several techniques have been used to collect the kinetics data. These include laminar jet falling film, rapid mixing,
falling film, diffusion across a porous media, and stirred reactor. Descriptions of the methodology and experimental set
up are given by Van Krevelen and Hoftijzer (1948), Nunge and Gill (1963), Coldrey and Harris (1976), Alvarez et al.
(1980), Glasscock (1990), Hogendoorn et al. (1993), and Ko and Li (2000).
The MEA reaction with CO2 has been studied
by several researchers including Astarita 1961, Leder 1971,
Sada et al. 1976, Hikita et al. 1977, Laddha and Danckwerts, 1981 and Blauwhoff et al. 1984. There is a general agreement
among the researchers that the reaction of CO2 with MEA follows a second order kinetics. The second order rate
constant of this reaction was correlated as a function of temperature by Hikita et al. 1977. The revision of the data made
by Blauwhoff et al. 1984 and Barth et al. 1986 supported the results of Hikita et al. 1977.
Blanc and Demarais (1984) revised the data and the
proposed mechanisms for the rate of reaction of CO2
with DEA. They realized that the researchers results vary significantly. The dependence of the reaction rate on the
concentration of DEA was reported as first or second order. The reported rate constants were also not comparable.
Blauwhoff et al. (1984) revised the reported kinetics data for this system. They concluded that the reaction rate of
CO2 with DEA is too complicated to be interpreted by a simple kinetic model. They further showed that the
zwitterion mechanism reconciles most of the CO2-DEA published kinetics data. The zwitterion mechanism was
adopted by Glasscock (1990) to represent the kinetics data of CO2 in primary and secondary alkanolamines.
This mechanism was originally proposed by Caplow in 1968 and introduced to the chemical engineering literature by
Danckwerts in 1979. According to this mechanism, CO2 reacts with MEA or DEA to form an unstable zwitterion, Z.
The zwitterion is instantaneously neutralized by any base, Bi, present in the solution to form the amine
carbamate and a protonated base, BiH+:
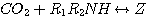
(3.14)

(3.15)
where Z ≡ R1R2NH+, R1 ≡ CH3CH2OH,
and R2 ≡ H and R1 for MEA and DEA, respectively. Reaction 3.14 is the rate controlling step;
hence the rate of disappearance of CO2 is given by:
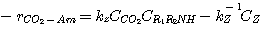
(3.16)
Since, the zwitterion is unstable, its rate of
formation is zero:

(3.17)
Solving for the concentration of the zwitterion
gives:
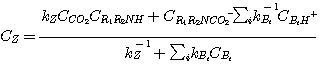
(3.18)
Substituting equation 3.18 into equation 3.16 and rearranging gives:

(3.19)
Equation 3.19 can be simplified by relating the groups of rate constants to their corresponding equilibrium
constants as follows. Consider the water reaction with a base:
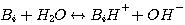
(3.20)
This reaction involves a proton transfer, therefore, the reactants and products of this reaction are always at local
equilibrium:
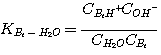
(3.21)
or:
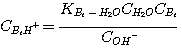
(3.22)
The amine can act as a base and reacts with water according to:

(3.23)
where:

(3.24)
Combining reactions 3.20 and 3.23 gives:
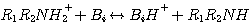
(3.25)
where:
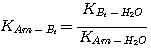
(3.26)
The reaction of amine with the zwitterion is given by:

(3.27)
Combining reactions 3.25 and 3.27 gives:
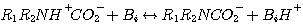
(3.28)
Comparing reactions 3.15 and 3.28 gives:
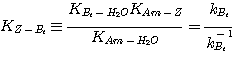
(3.29)
or:
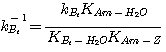
(3.30)
Adding reactions 3.14 and 3.15 and replacing with amine gives:

(3.31)
where:

(3.32)
or:

(3.33)
Substituting equations 3.24 and 3.33 into equation 3.30 gives:

(3.34)
Substituting equations 3.34 and 3.22 into equation 3.19 and rearranging gives:

(3.35)
The second term in the numerator of equation (3.35) represents the concentration of CO2 that is in is in
equilibrium with the amine, amine carbamate and protonated amine based on reaction 3.31. Hence, this equation can be
rewritten as:

(3.36)
As mentioned, the kinetics data for the CO2-MEA system follows a second order kinetics. Equation 3.35 is
reduced to
the second order form if the second term in the denominator is ignored in comparison to the first term, leading to:

(3.37)
The second order rate constant given by Hikita et al. 1977 will be used in this study to compute the CO2
absorption rate for systems containing MEA. This rate constant is expressed as a function of temperature by:
MEA:

(3.38)
In contrast, the first term in the denominator of equation (3.35) is negligible compared to the second term for the
CO2-DEA system:
DEA:

(3.39)
Equation 3.39 was used by Laddha and Danckwerts 1981, Blauwhoff et al. (1984), Versteeg and Van Swaaij (1988),
Critchfield (1988), and Glasscock (1990) to describe the kinetics data for the CO2-DEA system.
Glasscock (1990) assumed that the amine and the water are the only bases that contribute to the neutralization of the
zwitterion. The CO2-DEA rate expression reported by Glasscock 1990 will be utilized in this study.
This expression is given by
DEA:

(3.40)
The rate constants reported by Glasscock (1990) were extracted from the fit of the kinetics data and expressed as
functions of temperature according to

(3.41)

(3.42)
2.2 CO2 Reaction with MDEA
CO2 reacts indirectly with MDEA in the presence of water to form bicarbonate and protonated MDEA.
Three different mechanisms have been proposed for this reaction (Barth et al. 1981). The first mechanism suggests that
MDEA neutralizes the species formed by the CO2-water reactions (reactions 3.8 and 3.9). The second mechanism
assumes that MDEA associates with water before reacting with CO2:

(3.43)
The third mechanism follows the zwitterion mechanism described earlier for MEA and DEA:

(3.44)
The zwitterion formed immediately reacts with water and hydroxide to produce respectively bicarbonate and protonated
MDEA and bicarbonate and MDEA according to:
The third mechanism follows the zwitterion mechanism described earlier for MEA and DEA:

(3.45)

(3.46)
Adopting the third mechanism and following the procedure developed earlier for MEA and DEA, the following expression is
obtained for the rate of reaction of CO2 with MDEA:

(3.47)
Combining reactions 3.44 with 3.45 and 3.44 with 3.46 gives:

(3.48)

(3.49)
Reaction 3.48 can also be obtained from combinations of the following reactions:

(3.50)

(3.51)
Hence

(3.52)
Since reaction 3.50 is instantaneous, its products and reactants are at local equilibrium:

(3.53)
Therefore:

(3.54)
Reaction 3.49 can be obtained by combining the instantaneous water dissociation reaction (equation 2.1) with reaction
3.51 to obtain:

(3.55)
or:

(3.56)
Substituting equations 3.54 and 3.56 into equation 3.47 and rearranging gives:

(3.57)
or:

(3.58)
Similar to the derivation of MEA and DEA, the second term in the numerator of equation 3.58 represents the
concentration of CO2 which is in equilibrium with the bicarbonate and the hydroxide ions:

(3.59)
Equation 3.58 is a general rate expression for the reaction of CO2 with MDEA or any tertiary amine.
Depending on the magnitude of the second term of the denominator of this equation, one can obtain two limiting forms:

The rate expression in this case reduces to:

(3.60)
This form is essentially the expression, which would have been obtained if the second mechanism were used.
Many investigators including Haimor et al. (1987), Critchfield (1988), Tomcej et al. (1989), Little et al. (1990),
Rangwala et al. (1992), and Ko and Li (2000) adopted this form to fit the rate data of the CO2-MDEA system.
The rate constant of the reaction is given as a function of temperature by:

(3.61)
Comparison among the published values of the rate constant at 298.15 K shows a variation between 2.5 and 8.8
lit/mol/sec.

In this case the rate expression is given by:

(3.62)
Glasscock (1990) showed that this form reconciled the published rate data better.
He used activities instead of concentrations to obtain the rate constants. In the current study, the rate expression
represented by the first form (equation 3.60) with the rate constant reported by Critchfield (1988) will be used to model
the kinetics of the CO2 reaction with MDEA. The rate constant reported by Critchfield (1988) is given by:

(3.63)
2.3 CO2 Reaction with Blends of MEA-MDEA and DEA-MDEA
The absorption of CO2 in aqueous solution of blends of MEA-MDEA and DEA-MDEA was studied by Glasscock et
al. (1990), Versteeg et al. (1990), Rangwala et al. (1992), and Hagewiesche et al. (1995). Critchfield showed that the
interaction between MDEA and MEA is insignificant. Therefore the rate expressions (equation 3.37) for MEA and
(equation 3.60) for MDEA are still applicable for the mixture MEA-MDEA. However, for systems containing DEA and MDEA,
the latter acts as another base that neutralizes the zwitterion formed from the reaction of CO2 with DEA.
Hence, The CO2-DEA rate expression for systems containing DEA and MDEA should be corrected by adding the
contribution of MDEA to the neutralization of the zwitterion:
DEA/MDEA:

(3.64)

A value of 468 m6/kmol2/sec was reported in the thesis of Glasscock (1990) for the rate
constant k'R1R2R3N. In this work, this value will be used for
any temperature to compute the absorption rate of CO2in systems containing blends of DEA and MDEA.
Following the suggestion of Glasscock (1990), the effect of MDEA on the rate of reaction of CO2with MEA
will be ignored.
2.1 CO2 Reaction with MEA and DEA
The absorption of CO2 in aqueous solutions of
MEA and DEA has been extensively studied in the literature.
Several techniques have been used to collect the kinetics data. These include laminar jet falling film, rapid mixing,
falling film, diffusion across a porous media, and stirred reactor. Descriptions of the methodology and experimental set
up are given by Van Krevelen and Hoftijzer (1948), Nunge and Gill (1963), Coldrey and Harris (1976), Alvarez et al.
(1980), Glasscock (1990), Hogendoorn et al. (1993), and Ko and Li (2000).
The MEA reaction with CO2 has been studied
by several researchers including Astarita 1961, Leder 1971,
Sada et al. 1976, Hikita et al. 1977, Laddha and Danckwerts, 1981 and Blauwhoff et al. 1984. There is a general agreement
among the researchers that the reaction of CO2 with MEA follows a second order kinetics. The second order rate
constant of this reaction was correlated as a function of temperature by Hikita et al. 1977. The revision of the data made
by Blauwhoff et al. 1984 and Barth et al. 1986 supported the results of Hikita et al. 1977.
Blanc and Demarais (1984) revised the data and the
proposed mechanisms for the rate of reaction of CO2
with DEA. They realized that the researchers results vary significantly. The dependence of the reaction rate on the
concentration of DEA was reported as first or second order. The reported rate constants were also not comparable.
Blauwhoff et al. (1984) revised the reported kinetics data for this system. They concluded that the reaction rate of
CO2 with DEA is too complicated to be interpreted by a simple kinetic model. They further showed that the
zwitterion mechanism reconciles most of the CO2-DEA published kinetics data. The zwitterion mechanism was
adopted by Glasscock (1990) to represent the kinetics data of CO2 in primary and secondary alkanolamines.
This mechanism was originally proposed by Caplow in 1968 and introduced to the chemical engineering literature by
Danckwerts in 1979. According to this mechanism, CO2 reacts with MEA or DEA to form an unstable zwitterion, Z.
The zwitterion is instantaneously neutralized by any base, Bi, present in the solution to form the amine
carbamate and a protonated base, BiH+:
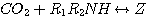
(3.14)

(3.15)
where Z ≡ R1R2NH+, R1 ≡ CH3CH2OH,
and R2 ≡ H and R1 for MEA and DEA, respectively. Reaction 3.14 is the rate controlling step;
hence the rate of disappearance of CO2 is given by:
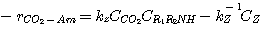
(3.16)
Since, the zwitterion is unstable, its rate of
formation is zero:

(3.17)
Solving for the concentration of the zwitterion
gives:
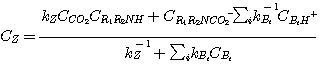
(3.18)
Substituting equation 3.18 into equation 3.16 and rearranging gives:

(3.19)
Equation 3.19 can be simplified by relating the groups of rate constants to their corresponding equilibrium
constants as follows. Consider the water reaction with a base:
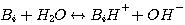
(3.20)
This reaction involves a proton transfer, therefore, the reactants and products of this reaction are always at local
equilibrium:
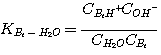
(3.21)
or:
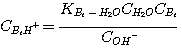
(3.22)
The amine can act as a base and reacts with water according to:

(3.23)
where:

(3.24)
Combining reactions 3.20 and 3.23 gives:
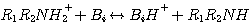
(3.25)
where:
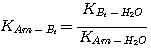
(3.26)
The reaction of amine with the zwitterion is given by:

(3.27)
Combining reactions 3.25 and 3.27 gives:
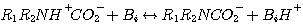
(3.28)
Comparing reactions 3.15 and 3.28 gives:
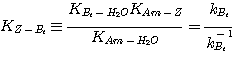
(3.29)
or:
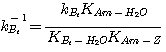
(3.30)
Adding reactions 3.14 and 3.15 and replacing with amine gives:

(3.31)
where:

(3.32)
or:

(3.33)
Substituting equations 3.24 and 3.33 into equation 3.30 gives:

(3.34)
Substituting equations 3.34 and 3.22 into equation 3.19 and rearranging gives:

(3.35)
The second term in the numerator of equation (3.35) represents the concentration of CO2 that is in is in
equilibrium with the amine, amine carbamate and protonated amine based on reaction 3.31. Hence, this equation can be
rewritten as:

(3.36)
As mentioned, the kinetics data for the CO2-MEA system follows a second order kinetics. Equation 3.35 is
reduced to
the second order form if the second term in the denominator is ignored in comparison to the first term, leading to:

(3.37)
The second order rate constant given by Hikita et al. 1977 will be used in this study to compute the CO2
absorption rate for systems containing MEA. This rate constant is expressed as a function of temperature by:
MEA:

(3.38)
In contrast, the first term in the denominator of equation (3.35) is negligible compared to the second term for the
CO2-DEA system:
DEA:

(3.39)
Equation 3.39 was used by Laddha and Danckwerts 1981, Blauwhoff et al. (1984), Versteeg and Van Swaaij (1988),
Critchfield (1988), and Glasscock (1990) to describe the kinetics data for the CO2-DEA system.
Glasscock (1990) assumed that the amine and the water are the only bases that contribute to the neutralization of the
zwitterion. The CO2-DEA rate expression reported by Glasscock 1990 will be utilized in this study.
This expression is given by
DEA:

(3.40)
The rate constants reported by Glasscock (1990) were extracted from the fit of the kinetics data and expressed as
functions of temperature according to

(3.41)

(3.42)
2.2 CO2 Reaction with MDEA
CO2 reacts indirectly with MDEA in the presence of water to form bicarbonate and protonated MDEA.
Three different mechanisms have been proposed for this reaction (Barth et al. 1981). The first mechanism suggests that
MDEA neutralizes the species formed by the CO2-water reactions (reactions 3.8 and 3.9). The second mechanism
assumes that MDEA associates with water before reacting with CO2:

(3.43)
The third mechanism follows the zwitterion mechanism described earlier for MEA and DEA:

(3.44)
The zwitterion formed immediately reacts with water and hydroxide to produce respectively bicarbonate and protonated
MDEA and bicarbonate and MDEA according to:
The third mechanism follows the zwitterion mechanism described earlier for MEA and DEA:

(3.45)

(3.46)
Adopting the third mechanism and following the procedure developed earlier for MEA and DEA, the following expression is
obtained for the rate of reaction of CO2 with MDEA:

(3.47)
Combining reactions 3.44 with 3.45 and 3.44 with 3.46 gives:

(3.48)

(3.49)
Reaction 3.48 can also be obtained from combinations of the following reactions:

(3.50)

(3.51)
Hence

(3.52)
Since reaction 3.50 is instantaneous, its products and reactants are at local equilibrium:

(3.53)
Therefore:

(3.54)
Reaction 3.49 can be obtained by combining the instantaneous water dissociation reaction (equation 2.1) with reaction
3.51 to obtain:

(3.55)
or:

(3.56)
Substituting equations 3.54 and 3.56 into equation 3.47 and rearranging gives:

(3.57)
or:

(3.58)
Similar to the derivation of MEA and DEA, the second term in the numerator of equation 3.58 represents the
concentration of CO2 which is in equilibrium with the bicarbonate and the hydroxide ions:

(3.59)
Equation 3.58 is a general rate expression for the reaction of CO2 with MDEA or any tertiary amine.
Depending on the magnitude of the second term of the denominator of this equation, one can obtain two limiting forms:

The rate expression in this case reduces to:

(3.60)
This form is essentially the expression, which would have been obtained if the second mechanism were used.
Many investigators including Haimor et al. (1987), Critchfield (1988), Tomcej et al. (1989), Little et al. (1990),
Rangwala et al. (1992), and Ko and Li (2000) adopted this form to fit the rate data of the CO2-MDEA system.
The rate constant of the reaction is given as a function of temperature by:

(3.61)
Comparison among the published values of the rate constant at 298.15 K shows a variation between 2.5 and 8.8
lit/mol/sec.

In this case the rate expression is given by:

(3.62)
Glasscock (1990) showed that this form reconciled the published rate data better.
He used activities instead of concentrations to obtain the rate constants. In the current study, the rate expression
represented by the first form (equation 3.60) with the rate constant reported by Critchfield (1988) will be used to model
the kinetics of the CO2 reaction with MDEA. The rate constant reported by Critchfield (1988) is given by:

(3.63)
2.3 CO2 Reaction with Blends of MEA-MDEA and DEA-MDEA
The absorption of CO2 in aqueous solution of blends of MEA-MDEA and DEA-MDEA was studied by Glasscock et
al. (1990), Versteeg et al. (1990), Rangwala et al. (1992), and Hagewiesche et al. (1995). Critchfield showed that the
interaction between MDEA and MEA is insignificant. Therefore the rate expressions (equation 3.37) for MEA and
(equation 3.60) for MDEA are still applicable for the mixture MEA-MDEA. However, for systems containing DEA and MDEA,
the latter acts as another base that neutralizes the zwitterion formed from the reaction of CO2 with DEA.
Hence, The CO2-DEA rate expression for systems containing DEA and MDEA should be corrected by adding the
contribution of MDEA to the neutralization of the zwitterion:
DEA/MDEA:

(3.64)

A value of 468 m6/kmol2/sec was reported in the thesis of Glasscock (1990) for the rate
constant k'R1R2R3N. In this work, this value will be used for
any temperature to compute the absorption rate of CO2in systems containing blends of DEA and MDEA.
Following the suggestion of Glasscock (1990), the effect of MDEA on the rate of reaction of CO2with MEA
will be ignored.
|
|
(3.14) |
|
|
(3.15) |
where Z ≡ R1R2NH+, R1 ≡ CH3CH2OH, and R2 ≡ H and R1 for MEA and DEA, respectively. Reaction 3.14 is the rate controlling step; hence the rate of disappearance of CO2 is given by:
|
|
(3.16) |
Since, the zwitterion is unstable, its rate of
formation is zero:

(3.17)
Solving for the concentration of the zwitterion
gives:
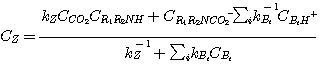
(3.18)
Substituting equation 3.18 into equation 3.16 and rearranging gives:

(3.19)
Equation 3.19 can be simplified by relating the groups of rate constants to their corresponding equilibrium
constants as follows. Consider the water reaction with a base:
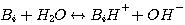
(3.20)
This reaction involves a proton transfer, therefore, the reactants and products of this reaction are always at local
equilibrium:
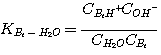
(3.21)
or:
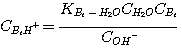
(3.22)
The amine can act as a base and reacts with water according to:

(3.23)
where:

(3.24)
Combining reactions 3.20 and 3.23 gives:
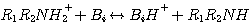
(3.25)
where:
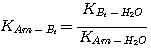
(3.26)
The reaction of amine with the zwitterion is given by:

(3.27)
Combining reactions 3.25 and 3.27 gives:
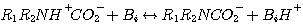
(3.28)
Comparing reactions 3.15 and 3.28 gives:
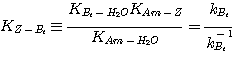
(3.29)
or:
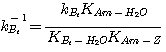
(3.30)
Adding reactions 3.14 and 3.15 and replacing with amine gives:

(3.31)
where:

(3.32)
or:

(3.33)
Substituting equations 3.24 and 3.33 into equation 3.30 gives:

(3.34)
Substituting equations 3.34 and 3.22 into equation 3.19 and rearranging gives:

(3.35)
The second term in the numerator of equation (3.35) represents the concentration of CO2 that is in is in
equilibrium with the amine, amine carbamate and protonated amine based on reaction 3.31. Hence, this equation can be
rewritten as:

(3.36)
As mentioned, the kinetics data for the CO2-MEA system follows a second order kinetics. Equation 3.35 is
reduced to
the second order form if the second term in the denominator is ignored in comparison to the first term, leading to:

(3.37)
The second order rate constant given by Hikita et al. 1977 will be used in this study to compute the CO2
absorption rate for systems containing MEA. This rate constant is expressed as a function of temperature by:
MEA:

(3.38)
In contrast, the first term in the denominator of equation (3.35) is negligible compared to the second term for the
CO2-DEA system:
DEA:

(3.39)
Equation 3.39 was used by Laddha and Danckwerts 1981, Blauwhoff et al. (1984), Versteeg and Van Swaaij (1988),
Critchfield (1988), and Glasscock (1990) to describe the kinetics data for the CO2-DEA system.
Glasscock (1990) assumed that the amine and the water are the only bases that contribute to the neutralization of the
zwitterion. The CO2-DEA rate expression reported by Glasscock 1990 will be utilized in this study.
This expression is given by
DEA:

(3.40)
The rate constants reported by Glasscock (1990) were extracted from the fit of the kinetics data and expressed as
functions of temperature according to

(3.41)

(3.42)
2.2 CO2 Reaction with MDEA
CO2 reacts indirectly with MDEA in the presence of water to form bicarbonate and protonated MDEA.
Three different mechanisms have been proposed for this reaction (Barth et al. 1981). The first mechanism suggests that
MDEA neutralizes the species formed by the CO2-water reactions (reactions 3.8 and 3.9). The second mechanism
assumes that MDEA associates with water before reacting with CO2:

(3.43)
The third mechanism follows the zwitterion mechanism described earlier for MEA and DEA:

(3.44)
The zwitterion formed immediately reacts with water and hydroxide to produce respectively bicarbonate and protonated
MDEA and bicarbonate and MDEA according to:
The third mechanism follows the zwitterion mechanism described earlier for MEA and DEA:

(3.45)

(3.46)
Adopting the third mechanism and following the procedure developed earlier for MEA and DEA, the following expression is
obtained for the rate of reaction of CO2 with MDEA:

(3.47)
Combining reactions 3.44 with 3.45 and 3.44 with 3.46 gives:

(3.48)

(3.49)
Reaction 3.48 can also be obtained from combinations of the following reactions:

(3.50)

(3.51)
Hence

(3.52)
Since reaction 3.50 is instantaneous, its products and reactants are at local equilibrium:

(3.53)
Therefore:

(3.54)
Reaction 3.49 can be obtained by combining the instantaneous water dissociation reaction (equation 2.1) with reaction
3.51 to obtain:

(3.55)
or:

(3.56)
Substituting equations 3.54 and 3.56 into equation 3.47 and rearranging gives:

(3.57)
or:

(3.58)
Similar to the derivation of MEA and DEA, the second term in the numerator of equation 3.58 represents the
concentration of CO2 which is in equilibrium with the bicarbonate and the hydroxide ions:

(3.59)
Equation 3.58 is a general rate expression for the reaction of CO2 with MDEA or any tertiary amine.
Depending on the magnitude of the second term of the denominator of this equation, one can obtain two limiting forms:

The rate expression in this case reduces to:

(3.60)
This form is essentially the expression, which would have been obtained if the second mechanism were used.
Many investigators including Haimor et al. (1987), Critchfield (1988), Tomcej et al. (1989), Little et al. (1990),
Rangwala et al. (1992), and Ko and Li (2000) adopted this form to fit the rate data of the CO2-MDEA system.
The rate constant of the reaction is given as a function of temperature by:

(3.61)
Comparison among the published values of the rate constant at 298.15 K shows a variation between 2.5 and 8.8
lit/mol/sec.

In this case the rate expression is given by:

(3.62)
Glasscock (1990) showed that this form reconciled the published rate data better.
He used activities instead of concentrations to obtain the rate constants. In the current study, the rate expression
represented by the first form (equation 3.60) with the rate constant reported by Critchfield (1988) will be used to model
the kinetics of the CO2 reaction with MDEA. The rate constant reported by Critchfield (1988) is given by:

(3.63)
2.3 CO2 Reaction with Blends of MEA-MDEA and DEA-MDEA
The absorption of CO2 in aqueous solution of blends of MEA-MDEA and DEA-MDEA was studied by Glasscock et
al. (1990), Versteeg et al. (1990), Rangwala et al. (1992), and Hagewiesche et al. (1995). Critchfield showed that the
interaction between MDEA and MEA is insignificant. Therefore the rate expressions (equation 3.37) for MEA and
(equation 3.60) for MDEA are still applicable for the mixture MEA-MDEA. However, for systems containing DEA and MDEA,
the latter acts as another base that neutralizes the zwitterion formed from the reaction of CO2 with DEA.
Hence, The CO2-DEA rate expression for systems containing DEA and MDEA should be corrected by adding the
contribution of MDEA to the neutralization of the zwitterion:
DEA/MDEA:

(3.64)

A value of 468 m6/kmol2/sec was reported in the thesis of Glasscock (1990) for the rate
constant k'R1R2R3N. In this work, this value will be used for
any temperature to compute the absorption rate of CO2in systems containing blends of DEA and MDEA.
Following the suggestion of Glasscock (1990), the effect of MDEA on the rate of reaction of CO2with MEA
will be ignored.
|
|
(3.17) |
Solving for the concentration of the zwitterion
gives:
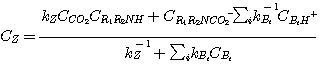
(3.18)
Substituting equation 3.18 into equation 3.16 and rearranging gives:

(3.19)
Equation 3.19 can be simplified by relating the groups of rate constants to their corresponding equilibrium
constants as follows. Consider the water reaction with a base:
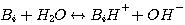
(3.20)
This reaction involves a proton transfer, therefore, the reactants and products of this reaction are always at local
equilibrium:
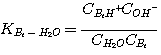
(3.21)
or:
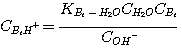
(3.22)
The amine can act as a base and reacts with water according to:

(3.23)
where:

(3.24)
Combining reactions 3.20 and 3.23 gives:
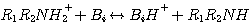
(3.25)
where:
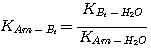
(3.26)
The reaction of amine with the zwitterion is given by:

(3.27)
Combining reactions 3.25 and 3.27 gives:
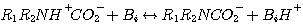
(3.28)
Comparing reactions 3.15 and 3.28 gives:
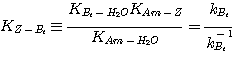
(3.29)
or:
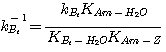
(3.30)
Adding reactions 3.14 and 3.15 and replacing with amine gives:

(3.31)
where:

(3.32)
or:

(3.33)
Substituting equations 3.24 and 3.33 into equation 3.30 gives:

(3.34)
Substituting equations 3.34 and 3.22 into equation 3.19 and rearranging gives:

(3.35)
The second term in the numerator of equation (3.35) represents the concentration of CO2 that is in is in
equilibrium with the amine, amine carbamate and protonated amine based on reaction 3.31. Hence, this equation can be
rewritten as:

(3.36)
As mentioned, the kinetics data for the CO2-MEA system follows a second order kinetics. Equation 3.35 is
reduced to
the second order form if the second term in the denominator is ignored in comparison to the first term, leading to:

(3.37)
The second order rate constant given by Hikita et al. 1977 will be used in this study to compute the CO2
absorption rate for systems containing MEA. This rate constant is expressed as a function of temperature by:
MEA:

(3.38)
In contrast, the first term in the denominator of equation (3.35) is negligible compared to the second term for the
CO2-DEA system:
DEA:

(3.39)
Equation 3.39 was used by Laddha and Danckwerts 1981, Blauwhoff et al. (1984), Versteeg and Van Swaaij (1988),
Critchfield (1988), and Glasscock (1990) to describe the kinetics data for the CO2-DEA system.
Glasscock (1990) assumed that the amine and the water are the only bases that contribute to the neutralization of the
zwitterion. The CO2-DEA rate expression reported by Glasscock 1990 will be utilized in this study.
This expression is given by
DEA:

(3.40)
The rate constants reported by Glasscock (1990) were extracted from the fit of the kinetics data and expressed as
functions of temperature according to

(3.41)

(3.42)
2.2 CO2 Reaction with MDEA
CO2 reacts indirectly with MDEA in the presence of water to form bicarbonate and protonated MDEA.
Three different mechanisms have been proposed for this reaction (Barth et al. 1981). The first mechanism suggests that
MDEA neutralizes the species formed by the CO2-water reactions (reactions 3.8 and 3.9). The second mechanism
assumes that MDEA associates with water before reacting with CO2:

(3.43)
The third mechanism follows the zwitterion mechanism described earlier for MEA and DEA:

(3.44)
The zwitterion formed immediately reacts with water and hydroxide to produce respectively bicarbonate and protonated
MDEA and bicarbonate and MDEA according to:
The third mechanism follows the zwitterion mechanism described earlier for MEA and DEA:

(3.45)

(3.46)
Adopting the third mechanism and following the procedure developed earlier for MEA and DEA, the following expression is
obtained for the rate of reaction of CO2 with MDEA:

(3.47)
Combining reactions 3.44 with 3.45 and 3.44 with 3.46 gives:

(3.48)

(3.49)
Reaction 3.48 can also be obtained from combinations of the following reactions:

(3.50)

(3.51)
Hence

(3.52)
Since reaction 3.50 is instantaneous, its products and reactants are at local equilibrium:

(3.53)
Therefore:

(3.54)
Reaction 3.49 can be obtained by combining the instantaneous water dissociation reaction (equation 2.1) with reaction
3.51 to obtain:

(3.55)
or:

(3.56)
Substituting equations 3.54 and 3.56 into equation 3.47 and rearranging gives:

(3.57)
or:

(3.58)
Similar to the derivation of MEA and DEA, the second term in the numerator of equation 3.58 represents the
concentration of CO2 which is in equilibrium with the bicarbonate and the hydroxide ions:

(3.59)
Equation 3.58 is a general rate expression for the reaction of CO2 with MDEA or any tertiary amine.
Depending on the magnitude of the second term of the denominator of this equation, one can obtain two limiting forms:

The rate expression in this case reduces to:

(3.60)
This form is essentially the expression, which would have been obtained if the second mechanism were used.
Many investigators including Haimor et al. (1987), Critchfield (1988), Tomcej et al. (1989), Little et al. (1990),
Rangwala et al. (1992), and Ko and Li (2000) adopted this form to fit the rate data of the CO2-MDEA system.
The rate constant of the reaction is given as a function of temperature by:

(3.61)
Comparison among the published values of the rate constant at 298.15 K shows a variation between 2.5 and 8.8
lit/mol/sec.

In this case the rate expression is given by:

(3.62)
Glasscock (1990) showed that this form reconciled the published rate data better.
He used activities instead of concentrations to obtain the rate constants. In the current study, the rate expression
represented by the first form (equation 3.60) with the rate constant reported by Critchfield (1988) will be used to model
the kinetics of the CO2 reaction with MDEA. The rate constant reported by Critchfield (1988) is given by:

(3.63)
2.3 CO2 Reaction with Blends of MEA-MDEA and DEA-MDEA
The absorption of CO2 in aqueous solution of blends of MEA-MDEA and DEA-MDEA was studied by Glasscock et
al. (1990), Versteeg et al. (1990), Rangwala et al. (1992), and Hagewiesche et al. (1995). Critchfield showed that the
interaction between MDEA and MEA is insignificant. Therefore the rate expressions (equation 3.37) for MEA and
(equation 3.60) for MDEA are still applicable for the mixture MEA-MDEA. However, for systems containing DEA and MDEA,
the latter acts as another base that neutralizes the zwitterion formed from the reaction of CO2 with DEA.
Hence, The CO2-DEA rate expression for systems containing DEA and MDEA should be corrected by adding the
contribution of MDEA to the neutralization of the zwitterion:
DEA/MDEA:

(3.64)

A value of 468 m6/kmol2/sec was reported in the thesis of Glasscock (1990) for the rate
constant k'R1R2R3N. In this work, this value will be used for
any temperature to compute the absorption rate of CO2in systems containing blends of DEA and MDEA.
Following the suggestion of Glasscock (1990), the effect of MDEA on the rate of reaction of CO2with MEA
will be ignored.
|
|
(3.18) |
Substituting equation 3.18 into equation 3.16 and rearranging gives:

(3.19)
Equation 3.19 can be simplified by relating the groups of rate constants to their corresponding equilibrium
constants as follows. Consider the water reaction with a base:
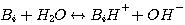
(3.20)
This reaction involves a proton transfer, therefore, the reactants and products of this reaction are always at local
equilibrium:
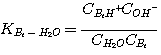
(3.21)
or:
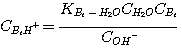
(3.22)
The amine can act as a base and reacts with water according to:

(3.23)
where:

(3.24)
Combining reactions 3.20 and 3.23 gives:
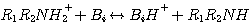
(3.25)
where:
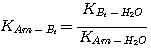
(3.26)
The reaction of amine with the zwitterion is given by:

(3.27)
Combining reactions 3.25 and 3.27 gives:
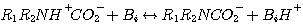
(3.28)
Comparing reactions 3.15 and 3.28 gives:
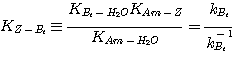
(3.29)
or:
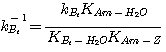
(3.30)
Adding reactions 3.14 and 3.15 and replacing with amine gives:

(3.31)
where:

(3.32)
or:

(3.33)
Substituting equations 3.24 and 3.33 into equation 3.30 gives:

(3.34)
Substituting equations 3.34 and 3.22 into equation 3.19 and rearranging gives:

(3.35)
The second term in the numerator of equation (3.35) represents the concentration of CO2 that is in is in
equilibrium with the amine, amine carbamate and protonated amine based on reaction 3.31. Hence, this equation can be
rewritten as:

(3.36)
As mentioned, the kinetics data for the CO2-MEA system follows a second order kinetics. Equation 3.35 is
reduced to
the second order form if the second term in the denominator is ignored in comparison to the first term, leading to:

(3.37)
The second order rate constant given by Hikita et al. 1977 will be used in this study to compute the CO2
absorption rate for systems containing MEA. This rate constant is expressed as a function of temperature by:
MEA:

(3.38)
In contrast, the first term in the denominator of equation (3.35) is negligible compared to the second term for the
CO2-DEA system:
DEA:

(3.39)
Equation 3.39 was used by Laddha and Danckwerts 1981, Blauwhoff et al. (1984), Versteeg and Van Swaaij (1988),
Critchfield (1988), and Glasscock (1990) to describe the kinetics data for the CO2-DEA system.
Glasscock (1990) assumed that the amine and the water are the only bases that contribute to the neutralization of the
zwitterion. The CO2-DEA rate expression reported by Glasscock 1990 will be utilized in this study.
This expression is given by
DEA:

(3.40)
The rate constants reported by Glasscock (1990) were extracted from the fit of the kinetics data and expressed as
functions of temperature according to

(3.41)

(3.42)
2.2 CO2 Reaction with MDEA
CO2 reacts indirectly with MDEA in the presence of water to form bicarbonate and protonated MDEA.
Three different mechanisms have been proposed for this reaction (Barth et al. 1981). The first mechanism suggests that
MDEA neutralizes the species formed by the CO2-water reactions (reactions 3.8 and 3.9). The second mechanism
assumes that MDEA associates with water before reacting with CO2:

(3.43)
The third mechanism follows the zwitterion mechanism described earlier for MEA and DEA:

(3.44)
The zwitterion formed immediately reacts with water and hydroxide to produce respectively bicarbonate and protonated
MDEA and bicarbonate and MDEA according to:
The third mechanism follows the zwitterion mechanism described earlier for MEA and DEA:

(3.45)

(3.46)
Adopting the third mechanism and following the procedure developed earlier for MEA and DEA, the following expression is
obtained for the rate of reaction of CO2 with MDEA:

(3.47)
Combining reactions 3.44 with 3.45 and 3.44 with 3.46 gives:

(3.48)

(3.49)
Reaction 3.48 can also be obtained from combinations of the following reactions:

(3.50)

(3.51)
Hence

(3.52)
Since reaction 3.50 is instantaneous, its products and reactants are at local equilibrium:

(3.53)
Therefore:

(3.54)
Reaction 3.49 can be obtained by combining the instantaneous water dissociation reaction (equation 2.1) with reaction
3.51 to obtain:

(3.55)
or:

(3.56)
Substituting equations 3.54 and 3.56 into equation 3.47 and rearranging gives:

(3.57)
or:

(3.58)
Similar to the derivation of MEA and DEA, the second term in the numerator of equation 3.58 represents the
concentration of CO2 which is in equilibrium with the bicarbonate and the hydroxide ions:

(3.59)
Equation 3.58 is a general rate expression for the reaction of CO2 with MDEA or any tertiary amine.
Depending on the magnitude of the second term of the denominator of this equation, one can obtain two limiting forms:

The rate expression in this case reduces to:

(3.60)
This form is essentially the expression, which would have been obtained if the second mechanism were used.
Many investigators including Haimor et al. (1987), Critchfield (1988), Tomcej et al. (1989), Little et al. (1990),
Rangwala et al. (1992), and Ko and Li (2000) adopted this form to fit the rate data of the CO2-MDEA system.
The rate constant of the reaction is given as a function of temperature by:

(3.61)
Comparison among the published values of the rate constant at 298.15 K shows a variation between 2.5 and 8.8
lit/mol/sec.

In this case the rate expression is given by:

(3.62)
Glasscock (1990) showed that this form reconciled the published rate data better.
He used activities instead of concentrations to obtain the rate constants. In the current study, the rate expression
represented by the first form (equation 3.60) with the rate constant reported by Critchfield (1988) will be used to model
the kinetics of the CO2 reaction with MDEA. The rate constant reported by Critchfield (1988) is given by:

(3.63)
2.3 CO2 Reaction with Blends of MEA-MDEA and DEA-MDEA
The absorption of CO2 in aqueous solution of blends of MEA-MDEA and DEA-MDEA was studied by Glasscock et
al. (1990), Versteeg et al. (1990), Rangwala et al. (1992), and Hagewiesche et al. (1995). Critchfield showed that the
interaction between MDEA and MEA is insignificant. Therefore the rate expressions (equation 3.37) for MEA and
(equation 3.60) for MDEA are still applicable for the mixture MEA-MDEA. However, for systems containing DEA and MDEA,
the latter acts as another base that neutralizes the zwitterion formed from the reaction of CO2 with DEA.
Hence, The CO2-DEA rate expression for systems containing DEA and MDEA should be corrected by adding the
contribution of MDEA to the neutralization of the zwitterion:
DEA/MDEA:

(3.64)

A value of 468 m6/kmol2/sec was reported in the thesis of Glasscock (1990) for the rate
constant k'R1R2R3N. In this work, this value will be used for
any temperature to compute the absorption rate of CO2in systems containing blends of DEA and MDEA.
Following the suggestion of Glasscock (1990), the effect of MDEA on the rate of reaction of CO2with MEA
will be ignored.
|
|
(3.19) |
Equation 3.19 can be simplified by relating the groups of rate constants to their corresponding equilibrium
constants as follows. Consider the water reaction with a base:
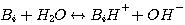
(3.20)
This reaction involves a proton transfer, therefore, the reactants and products of this reaction are always at local
equilibrium:
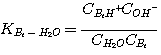
(3.21)
or:
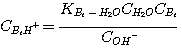
(3.22)
The amine can act as a base and reacts with water according to:

(3.23)
where:

(3.24)
Combining reactions 3.20 and 3.23 gives:
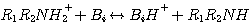
(3.25)
where:
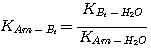
(3.26)
The reaction of amine with the zwitterion is given by:

(3.27)
Combining reactions 3.25 and 3.27 gives:
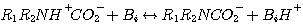
(3.28)
Comparing reactions 3.15 and 3.28 gives:
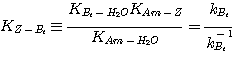
(3.29)
or:
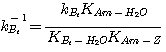
(3.30)
Adding reactions 3.14 and 3.15 and replacing with amine gives:

(3.31)
where:

(3.32)
or:

(3.33)
Substituting equations 3.24 and 3.33 into equation 3.30 gives:

(3.34)
Substituting equations 3.34 and 3.22 into equation 3.19 and rearranging gives:

(3.35)
The second term in the numerator of equation (3.35) represents the concentration of CO2 that is in is in
equilibrium with the amine, amine carbamate and protonated amine based on reaction 3.31. Hence, this equation can be
rewritten as:

(3.36)
As mentioned, the kinetics data for the CO2-MEA system follows a second order kinetics. Equation 3.35 is
reduced to
the second order form if the second term in the denominator is ignored in comparison to the first term, leading to:

(3.37)
The second order rate constant given by Hikita et al. 1977 will be used in this study to compute the CO2
absorption rate for systems containing MEA. This rate constant is expressed as a function of temperature by:
MEA:

(3.38)
In contrast, the first term in the denominator of equation (3.35) is negligible compared to the second term for the
CO2-DEA system:
DEA:

(3.39)
Equation 3.39 was used by Laddha and Danckwerts 1981, Blauwhoff et al. (1984), Versteeg and Van Swaaij (1988),
Critchfield (1988), and Glasscock (1990) to describe the kinetics data for the CO2-DEA system.
Glasscock (1990) assumed that the amine and the water are the only bases that contribute to the neutralization of the
zwitterion. The CO2-DEA rate expression reported by Glasscock 1990 will be utilized in this study.
This expression is given by
DEA:

(3.40)
The rate constants reported by Glasscock (1990) were extracted from the fit of the kinetics data and expressed as
functions of temperature according to

(3.41)

(3.42)
2.2 CO2 Reaction with MDEA
CO2 reacts indirectly with MDEA in the presence of water to form bicarbonate and protonated MDEA.
Three different mechanisms have been proposed for this reaction (Barth et al. 1981). The first mechanism suggests that
MDEA neutralizes the species formed by the CO2-water reactions (reactions 3.8 and 3.9). The second mechanism
assumes that MDEA associates with water before reacting with CO2:

(3.43)
The third mechanism follows the zwitterion mechanism described earlier for MEA and DEA:

(3.44)
The zwitterion formed immediately reacts with water and hydroxide to produce respectively bicarbonate and protonated
MDEA and bicarbonate and MDEA according to:
The third mechanism follows the zwitterion mechanism described earlier for MEA and DEA:

(3.45)

(3.46)
Adopting the third mechanism and following the procedure developed earlier for MEA and DEA, the following expression is
obtained for the rate of reaction of CO2 with MDEA:

(3.47)
Combining reactions 3.44 with 3.45 and 3.44 with 3.46 gives:

(3.48)

(3.49)
Reaction 3.48 can also be obtained from combinations of the following reactions:

(3.50)

(3.51)
Hence

(3.52)
Since reaction 3.50 is instantaneous, its products and reactants are at local equilibrium:

(3.53)
Therefore:

(3.54)
Reaction 3.49 can be obtained by combining the instantaneous water dissociation reaction (equation 2.1) with reaction
3.51 to obtain:

(3.55)
or:

(3.56)
Substituting equations 3.54 and 3.56 into equation 3.47 and rearranging gives:

(3.57)
or:

(3.58)
Similar to the derivation of MEA and DEA, the second term in the numerator of equation 3.58 represents the
concentration of CO2 which is in equilibrium with the bicarbonate and the hydroxide ions:

(3.59)
Equation 3.58 is a general rate expression for the reaction of CO2 with MDEA or any tertiary amine.
Depending on the magnitude of the second term of the denominator of this equation, one can obtain two limiting forms:

The rate expression in this case reduces to:

(3.60)
This form is essentially the expression, which would have been obtained if the second mechanism were used.
Many investigators including Haimor et al. (1987), Critchfield (1988), Tomcej et al. (1989), Little et al. (1990),
Rangwala et al. (1992), and Ko and Li (2000) adopted this form to fit the rate data of the CO2-MDEA system.
The rate constant of the reaction is given as a function of temperature by:

(3.61)
Comparison among the published values of the rate constant at 298.15 K shows a variation between 2.5 and 8.8
lit/mol/sec.

In this case the rate expression is given by:

(3.62)
Glasscock (1990) showed that this form reconciled the published rate data better.
He used activities instead of concentrations to obtain the rate constants. In the current study, the rate expression
represented by the first form (equation 3.60) with the rate constant reported by Critchfield (1988) will be used to model
the kinetics of the CO2 reaction with MDEA. The rate constant reported by Critchfield (1988) is given by:

(3.63)
2.3 CO2 Reaction with Blends of MEA-MDEA and DEA-MDEA
The absorption of CO2 in aqueous solution of blends of MEA-MDEA and DEA-MDEA was studied by Glasscock et
al. (1990), Versteeg et al. (1990), Rangwala et al. (1992), and Hagewiesche et al. (1995). Critchfield showed that the
interaction between MDEA and MEA is insignificant. Therefore the rate expressions (equation 3.37) for MEA and
(equation 3.60) for MDEA are still applicable for the mixture MEA-MDEA. However, for systems containing DEA and MDEA,
the latter acts as another base that neutralizes the zwitterion formed from the reaction of CO2 with DEA.
Hence, The CO2-DEA rate expression for systems containing DEA and MDEA should be corrected by adding the
contribution of MDEA to the neutralization of the zwitterion:
DEA/MDEA:

(3.64)

A value of 468 m6/kmol2/sec was reported in the thesis of Glasscock (1990) for the rate
constant k'R1R2R3N. In this work, this value will be used for
any temperature to compute the absorption rate of CO2in systems containing blends of DEA and MDEA.
Following the suggestion of Glasscock (1990), the effect of MDEA on the rate of reaction of CO2with MEA
will be ignored.
|
|
(3.20) |
This reaction involves a proton transfer, therefore, the reactants and products of this reaction are always at local
equilibrium:
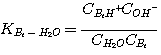
(3.21)
or:
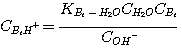
(3.22)
The amine can act as a base and reacts with water according to:

(3.23)
where:

(3.24)
Combining reactions 3.20 and 3.23 gives:
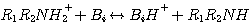
(3.25)
where:
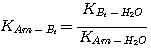
(3.26)
The reaction of amine with the zwitterion is given by:

(3.27)
Combining reactions 3.25 and 3.27 gives:
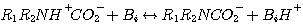
(3.28)
Comparing reactions 3.15 and 3.28 gives:
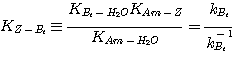
(3.29)
or:
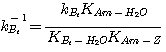
(3.30)
Adding reactions 3.14 and 3.15 and replacing with amine gives:

(3.31)
where:

(3.32)
or:

(3.33)
Substituting equations 3.24 and 3.33 into equation 3.30 gives:

(3.34)
Substituting equations 3.34 and 3.22 into equation 3.19 and rearranging gives:

(3.35)
The second term in the numerator of equation (3.35) represents the concentration of CO2 that is in is in
equilibrium with the amine, amine carbamate and protonated amine based on reaction 3.31. Hence, this equation can be
rewritten as:

(3.36)
As mentioned, the kinetics data for the CO2-MEA system follows a second order kinetics. Equation 3.35 is
reduced to
the second order form if the second term in the denominator is ignored in comparison to the first term, leading to:

(3.37)
The second order rate constant given by Hikita et al. 1977 will be used in this study to compute the CO2
absorption rate for systems containing MEA. This rate constant is expressed as a function of temperature by:
MEA:

(3.38)
In contrast, the first term in the denominator of equation (3.35) is negligible compared to the second term for the
CO2-DEA system:
DEA:

(3.39)
Equation 3.39 was used by Laddha and Danckwerts 1981, Blauwhoff et al. (1984), Versteeg and Van Swaaij (1988),
Critchfield (1988), and Glasscock (1990) to describe the kinetics data for the CO2-DEA system.
Glasscock (1990) assumed that the amine and the water are the only bases that contribute to the neutralization of the
zwitterion. The CO2-DEA rate expression reported by Glasscock 1990 will be utilized in this study.
This expression is given by
DEA:

(3.40)
The rate constants reported by Glasscock (1990) were extracted from the fit of the kinetics data and expressed as
functions of temperature according to

(3.41)

(3.42)
2.2 CO2 Reaction with MDEA
CO2 reacts indirectly with MDEA in the presence of water to form bicarbonate and protonated MDEA.
Three different mechanisms have been proposed for this reaction (Barth et al. 1981). The first mechanism suggests that
MDEA neutralizes the species formed by the CO2-water reactions (reactions 3.8 and 3.9). The second mechanism
assumes that MDEA associates with water before reacting with CO2:

(3.43)
The third mechanism follows the zwitterion mechanism described earlier for MEA and DEA:

(3.44)
The zwitterion formed immediately reacts with water and hydroxide to produce respectively bicarbonate and protonated
MDEA and bicarbonate and MDEA according to:
The third mechanism follows the zwitterion mechanism described earlier for MEA and DEA:

(3.45)

(3.46)
Adopting the third mechanism and following the procedure developed earlier for MEA and DEA, the following expression is
obtained for the rate of reaction of CO2 with MDEA:

(3.47)
Combining reactions 3.44 with 3.45 and 3.44 with 3.46 gives:

(3.48)

(3.49)
Reaction 3.48 can also be obtained from combinations of the following reactions:

(3.50)

(3.51)
Hence

(3.52)
Since reaction 3.50 is instantaneous, its products and reactants are at local equilibrium:

(3.53)
Therefore:

(3.54)
Reaction 3.49 can be obtained by combining the instantaneous water dissociation reaction (equation 2.1) with reaction
3.51 to obtain:

(3.55)
or:

(3.56)
Substituting equations 3.54 and 3.56 into equation 3.47 and rearranging gives:

(3.57)
or:

(3.58)
Similar to the derivation of MEA and DEA, the second term in the numerator of equation 3.58 represents the
concentration of CO2 which is in equilibrium with the bicarbonate and the hydroxide ions:

(3.59)
Equation 3.58 is a general rate expression for the reaction of CO2 with MDEA or any tertiary amine.
Depending on the magnitude of the second term of the denominator of this equation, one can obtain two limiting forms:

The rate expression in this case reduces to:

(3.60)
This form is essentially the expression, which would have been obtained if the second mechanism were used.
Many investigators including Haimor et al. (1987), Critchfield (1988), Tomcej et al. (1989), Little et al. (1990),
Rangwala et al. (1992), and Ko and Li (2000) adopted this form to fit the rate data of the CO2-MDEA system.
The rate constant of the reaction is given as a function of temperature by:

(3.61)
Comparison among the published values of the rate constant at 298.15 K shows a variation between 2.5 and 8.8
lit/mol/sec.

In this case the rate expression is given by:

(3.62)
Glasscock (1990) showed that this form reconciled the published rate data better.
He used activities instead of concentrations to obtain the rate constants. In the current study, the rate expression
represented by the first form (equation 3.60) with the rate constant reported by Critchfield (1988) will be used to model
the kinetics of the CO2 reaction with MDEA. The rate constant reported by Critchfield (1988) is given by:

(3.63)
2.3 CO2 Reaction with Blends of MEA-MDEA and DEA-MDEA
The absorption of CO2 in aqueous solution of blends of MEA-MDEA and DEA-MDEA was studied by Glasscock et
al. (1990), Versteeg et al. (1990), Rangwala et al. (1992), and Hagewiesche et al. (1995). Critchfield showed that the
interaction between MDEA and MEA is insignificant. Therefore the rate expressions (equation 3.37) for MEA and
(equation 3.60) for MDEA are still applicable for the mixture MEA-MDEA. However, for systems containing DEA and MDEA,
the latter acts as another base that neutralizes the zwitterion formed from the reaction of CO2 with DEA.
Hence, The CO2-DEA rate expression for systems containing DEA and MDEA should be corrected by adding the
contribution of MDEA to the neutralization of the zwitterion:
DEA/MDEA:

(3.64)

A value of 468 m6/kmol2/sec was reported in the thesis of Glasscock (1990) for the rate
constant k'R1R2R3N. In this work, this value will be used for
any temperature to compute the absorption rate of CO2in systems containing blends of DEA and MDEA.
Following the suggestion of Glasscock (1990), the effect of MDEA on the rate of reaction of CO2with MEA
will be ignored.
|
|
(3.21) |
or:
|
|
(3.22) |
The amine can act as a base and reacts with water according to:

(3.23)
where:

(3.24)
Combining reactions 3.20 and 3.23 gives:
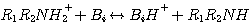
(3.25)
where:
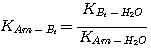
(3.26)
The reaction of amine with the zwitterion is given by:

(3.27)
Combining reactions 3.25 and 3.27 gives:
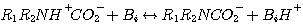
(3.28)
Comparing reactions 3.15 and 3.28 gives:
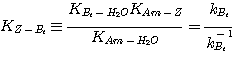
(3.29)
or:
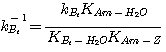
(3.30)
Adding reactions 3.14 and 3.15 and replacing with amine gives:

(3.31)
where:

(3.32)
or:

(3.33)
Substituting equations 3.24 and 3.33 into equation 3.30 gives:

(3.34)
Substituting equations 3.34 and 3.22 into equation 3.19 and rearranging gives:

(3.35)
The second term in the numerator of equation (3.35) represents the concentration of CO2 that is in is in
equilibrium with the amine, amine carbamate and protonated amine based on reaction 3.31. Hence, this equation can be
rewritten as:

(3.36)
As mentioned, the kinetics data for the CO2-MEA system follows a second order kinetics. Equation 3.35 is
reduced to
the second order form if the second term in the denominator is ignored in comparison to the first term, leading to:

(3.37)
The second order rate constant given by Hikita et al. 1977 will be used in this study to compute the CO2
absorption rate for systems containing MEA. This rate constant is expressed as a function of temperature by:
MEA:

(3.38)
In contrast, the first term in the denominator of equation (3.35) is negligible compared to the second term for the
CO2-DEA system:
DEA:

(3.39)
Equation 3.39 was used by Laddha and Danckwerts 1981, Blauwhoff et al. (1984), Versteeg and Van Swaaij (1988),
Critchfield (1988), and Glasscock (1990) to describe the kinetics data for the CO2-DEA system.
Glasscock (1990) assumed that the amine and the water are the only bases that contribute to the neutralization of the
zwitterion. The CO2-DEA rate expression reported by Glasscock 1990 will be utilized in this study.
This expression is given by
DEA:

(3.40)
The rate constants reported by Glasscock (1990) were extracted from the fit of the kinetics data and expressed as
functions of temperature according to

(3.41)

(3.42)
2.2 CO2 Reaction with MDEA
CO2 reacts indirectly with MDEA in the presence of water to form bicarbonate and protonated MDEA.
Three different mechanisms have been proposed for this reaction (Barth et al. 1981). The first mechanism suggests that
MDEA neutralizes the species formed by the CO2-water reactions (reactions 3.8 and 3.9). The second mechanism
assumes that MDEA associates with water before reacting with CO2:

(3.43)
The third mechanism follows the zwitterion mechanism described earlier for MEA and DEA:

(3.44)
The zwitterion formed immediately reacts with water and hydroxide to produce respectively bicarbonate and protonated
MDEA and bicarbonate and MDEA according to:
The third mechanism follows the zwitterion mechanism described earlier for MEA and DEA:

(3.45)

(3.46)
Adopting the third mechanism and following the procedure developed earlier for MEA and DEA, the following expression is
obtained for the rate of reaction of CO2 with MDEA:

(3.47)
Combining reactions 3.44 with 3.45 and 3.44 with 3.46 gives:

(3.48)

(3.49)
Reaction 3.48 can also be obtained from combinations of the following reactions:

(3.50)

(3.51)
Hence

(3.52)
Since reaction 3.50 is instantaneous, its products and reactants are at local equilibrium:

(3.53)
Therefore:

(3.54)
Reaction 3.49 can be obtained by combining the instantaneous water dissociation reaction (equation 2.1) with reaction
3.51 to obtain:

(3.55)
or:

(3.56)
Substituting equations 3.54 and 3.56 into equation 3.47 and rearranging gives:

(3.57)
or:

(3.58)
Similar to the derivation of MEA and DEA, the second term in the numerator of equation 3.58 represents the
concentration of CO2 which is in equilibrium with the bicarbonate and the hydroxide ions:

(3.59)
Equation 3.58 is a general rate expression for the reaction of CO2 with MDEA or any tertiary amine.
Depending on the magnitude of the second term of the denominator of this equation, one can obtain two limiting forms:

The rate expression in this case reduces to:

(3.60)
This form is essentially the expression, which would have been obtained if the second mechanism were used.
Many investigators including Haimor et al. (1987), Critchfield (1988), Tomcej et al. (1989), Little et al. (1990),
Rangwala et al. (1992), and Ko and Li (2000) adopted this form to fit the rate data of the CO2-MDEA system.
The rate constant of the reaction is given as a function of temperature by:

(3.61)
Comparison among the published values of the rate constant at 298.15 K shows a variation between 2.5 and 8.8
lit/mol/sec.

In this case the rate expression is given by:

(3.62)
Glasscock (1990) showed that this form reconciled the published rate data better.
He used activities instead of concentrations to obtain the rate constants. In the current study, the rate expression
represented by the first form (equation 3.60) with the rate constant reported by Critchfield (1988) will be used to model
the kinetics of the CO2 reaction with MDEA. The rate constant reported by Critchfield (1988) is given by:

(3.63)
2.3 CO2 Reaction with Blends of MEA-MDEA and DEA-MDEA
The absorption of CO2 in aqueous solution of blends of MEA-MDEA and DEA-MDEA was studied by Glasscock et
al. (1990), Versteeg et al. (1990), Rangwala et al. (1992), and Hagewiesche et al. (1995). Critchfield showed that the
interaction between MDEA and MEA is insignificant. Therefore the rate expressions (equation 3.37) for MEA and
(equation 3.60) for MDEA are still applicable for the mixture MEA-MDEA. However, for systems containing DEA and MDEA,
the latter acts as another base that neutralizes the zwitterion formed from the reaction of CO2 with DEA.
Hence, The CO2-DEA rate expression for systems containing DEA and MDEA should be corrected by adding the
contribution of MDEA to the neutralization of the zwitterion:
DEA/MDEA:

(3.64)

A value of 468 m6/kmol2/sec was reported in the thesis of Glasscock (1990) for the rate
constant k'R1R2R3N. In this work, this value will be used for
any temperature to compute the absorption rate of CO2in systems containing blends of DEA and MDEA.
Following the suggestion of Glasscock (1990), the effect of MDEA on the rate of reaction of CO2with MEA
will be ignored.
|
|
(3.23) |
where:
|
|
(3.24) |
Combining reactions 3.20 and 3.23 gives:
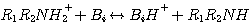
(3.25)
where:
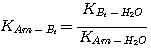
(3.26)
The reaction of amine with the zwitterion is given by:

(3.27)
Combining reactions 3.25 and 3.27 gives:
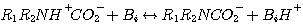
(3.28)
Comparing reactions 3.15 and 3.28 gives:
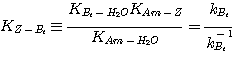
(3.29)
or:
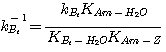
(3.30)
Adding reactions 3.14 and 3.15 and replacing with amine gives:

(3.31)
where:

(3.32)
or:

(3.33)
Substituting equations 3.24 and 3.33 into equation 3.30 gives:

(3.34)
Substituting equations 3.34 and 3.22 into equation 3.19 and rearranging gives:

(3.35)
The second term in the numerator of equation (3.35) represents the concentration of CO2 that is in is in
equilibrium with the amine, amine carbamate and protonated amine based on reaction 3.31. Hence, this equation can be
rewritten as:

(3.36)
As mentioned, the kinetics data for the CO2-MEA system follows a second order kinetics. Equation 3.35 is
reduced to
the second order form if the second term in the denominator is ignored in comparison to the first term, leading to:

(3.37)
The second order rate constant given by Hikita et al. 1977 will be used in this study to compute the CO2
absorption rate for systems containing MEA. This rate constant is expressed as a function of temperature by:
MEA:

(3.38)
In contrast, the first term in the denominator of equation (3.35) is negligible compared to the second term for the
CO2-DEA system:
DEA:

(3.39)
Equation 3.39 was used by Laddha and Danckwerts 1981, Blauwhoff et al. (1984), Versteeg and Van Swaaij (1988),
Critchfield (1988), and Glasscock (1990) to describe the kinetics data for the CO2-DEA system.
Glasscock (1990) assumed that the amine and the water are the only bases that contribute to the neutralization of the
zwitterion. The CO2-DEA rate expression reported by Glasscock 1990 will be utilized in this study.
This expression is given by
DEA:

(3.40)
The rate constants reported by Glasscock (1990) were extracted from the fit of the kinetics data and expressed as
functions of temperature according to

(3.41)

(3.42)
2.2 CO2 Reaction with MDEA
CO2 reacts indirectly with MDEA in the presence of water to form bicarbonate and protonated MDEA.
Three different mechanisms have been proposed for this reaction (Barth et al. 1981). The first mechanism suggests that
MDEA neutralizes the species formed by the CO2-water reactions (reactions 3.8 and 3.9). The second mechanism
assumes that MDEA associates with water before reacting with CO2:

(3.43)
The third mechanism follows the zwitterion mechanism described earlier for MEA and DEA:

(3.44)
The zwitterion formed immediately reacts with water and hydroxide to produce respectively bicarbonate and protonated
MDEA and bicarbonate and MDEA according to:
The third mechanism follows the zwitterion mechanism described earlier for MEA and DEA:

(3.45)

(3.46)
Adopting the third mechanism and following the procedure developed earlier for MEA and DEA, the following expression is
obtained for the rate of reaction of CO2 with MDEA:

(3.47)
Combining reactions 3.44 with 3.45 and 3.44 with 3.46 gives:

(3.48)

(3.49)
Reaction 3.48 can also be obtained from combinations of the following reactions:

(3.50)

(3.51)
Hence

(3.52)
Since reaction 3.50 is instantaneous, its products and reactants are at local equilibrium:

(3.53)
Therefore:

(3.54)
Reaction 3.49 can be obtained by combining the instantaneous water dissociation reaction (equation 2.1) with reaction
3.51 to obtain:

(3.55)
or:

(3.56)
Substituting equations 3.54 and 3.56 into equation 3.47 and rearranging gives:

(3.57)
or:

(3.58)
Similar to the derivation of MEA and DEA, the second term in the numerator of equation 3.58 represents the
concentration of CO2 which is in equilibrium with the bicarbonate and the hydroxide ions:

(3.59)
Equation 3.58 is a general rate expression for the reaction of CO2 with MDEA or any tertiary amine.
Depending on the magnitude of the second term of the denominator of this equation, one can obtain two limiting forms:

The rate expression in this case reduces to:

(3.60)
This form is essentially the expression, which would have been obtained if the second mechanism were used.
Many investigators including Haimor et al. (1987), Critchfield (1988), Tomcej et al. (1989), Little et al. (1990),
Rangwala et al. (1992), and Ko and Li (2000) adopted this form to fit the rate data of the CO2-MDEA system.
The rate constant of the reaction is given as a function of temperature by:

(3.61)
Comparison among the published values of the rate constant at 298.15 K shows a variation between 2.5 and 8.8
lit/mol/sec.

In this case the rate expression is given by:

(3.62)
Glasscock (1990) showed that this form reconciled the published rate data better.
He used activities instead of concentrations to obtain the rate constants. In the current study, the rate expression
represented by the first form (equation 3.60) with the rate constant reported by Critchfield (1988) will be used to model
the kinetics of the CO2 reaction with MDEA. The rate constant reported by Critchfield (1988) is given by:

(3.63)
2.3 CO2 Reaction with Blends of MEA-MDEA and DEA-MDEA
The absorption of CO2 in aqueous solution of blends of MEA-MDEA and DEA-MDEA was studied by Glasscock et
al. (1990), Versteeg et al. (1990), Rangwala et al. (1992), and Hagewiesche et al. (1995). Critchfield showed that the
interaction between MDEA and MEA is insignificant. Therefore the rate expressions (equation 3.37) for MEA and
(equation 3.60) for MDEA are still applicable for the mixture MEA-MDEA. However, for systems containing DEA and MDEA,
the latter acts as another base that neutralizes the zwitterion formed from the reaction of CO2 with DEA.
Hence, The CO2-DEA rate expression for systems containing DEA and MDEA should be corrected by adding the
contribution of MDEA to the neutralization of the zwitterion:
DEA/MDEA:

(3.64)

A value of 468 m6/kmol2/sec was reported in the thesis of Glasscock (1990) for the rate
constant k'R1R2R3N. In this work, this value will be used for
any temperature to compute the absorption rate of CO2in systems containing blends of DEA and MDEA.
Following the suggestion of Glasscock (1990), the effect of MDEA on the rate of reaction of CO2with MEA
will be ignored.
|
|
(3.25) |
where:
|
|
(3.26) |
The reaction of amine with the zwitterion is given by:

(3.27)
Combining reactions 3.25 and 3.27 gives:
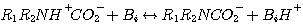
(3.28)
Comparing reactions 3.15 and 3.28 gives:
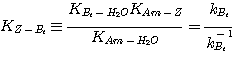
(3.29)
or:
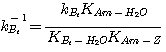
(3.30)
Adding reactions 3.14 and 3.15 and replacing with amine gives:

(3.31)
where:

(3.32)
or:

(3.33)
Substituting equations 3.24 and 3.33 into equation 3.30 gives:

(3.34)
Substituting equations 3.34 and 3.22 into equation 3.19 and rearranging gives:

(3.35)
The second term in the numerator of equation (3.35) represents the concentration of CO2 that is in is in
equilibrium with the amine, amine carbamate and protonated amine based on reaction 3.31. Hence, this equation can be
rewritten as:

(3.36)
As mentioned, the kinetics data for the CO2-MEA system follows a second order kinetics. Equation 3.35 is
reduced to
the second order form if the second term in the denominator is ignored in comparison to the first term, leading to:

(3.37)
The second order rate constant given by Hikita et al. 1977 will be used in this study to compute the CO2
absorption rate for systems containing MEA. This rate constant is expressed as a function of temperature by:
MEA:

(3.38)
In contrast, the first term in the denominator of equation (3.35) is negligible compared to the second term for the
CO2-DEA system:
DEA:

(3.39)
Equation 3.39 was used by Laddha and Danckwerts 1981, Blauwhoff et al. (1984), Versteeg and Van Swaaij (1988),
Critchfield (1988), and Glasscock (1990) to describe the kinetics data for the CO2-DEA system.
Glasscock (1990) assumed that the amine and the water are the only bases that contribute to the neutralization of the
zwitterion. The CO2-DEA rate expression reported by Glasscock 1990 will be utilized in this study.
This expression is given by
DEA:

(3.40)
The rate constants reported by Glasscock (1990) were extracted from the fit of the kinetics data and expressed as
functions of temperature according to

(3.41)

(3.42)
2.2 CO2 Reaction with MDEA
CO2 reacts indirectly with MDEA in the presence of water to form bicarbonate and protonated MDEA.
Three different mechanisms have been proposed for this reaction (Barth et al. 1981). The first mechanism suggests that
MDEA neutralizes the species formed by the CO2-water reactions (reactions 3.8 and 3.9). The second mechanism
assumes that MDEA associates with water before reacting with CO2:

(3.43)
The third mechanism follows the zwitterion mechanism described earlier for MEA and DEA:

(3.44)
The zwitterion formed immediately reacts with water and hydroxide to produce respectively bicarbonate and protonated
MDEA and bicarbonate and MDEA according to:
The third mechanism follows the zwitterion mechanism described earlier for MEA and DEA:

(3.45)

(3.46)
Adopting the third mechanism and following the procedure developed earlier for MEA and DEA, the following expression is
obtained for the rate of reaction of CO2 with MDEA:

(3.47)
Combining reactions 3.44 with 3.45 and 3.44 with 3.46 gives:

(3.48)

(3.49)
Reaction 3.48 can also be obtained from combinations of the following reactions:

(3.50)

(3.51)
Hence

(3.52)
Since reaction 3.50 is instantaneous, its products and reactants are at local equilibrium:

(3.53)
Therefore:

(3.54)
Reaction 3.49 can be obtained by combining the instantaneous water dissociation reaction (equation 2.1) with reaction
3.51 to obtain:

(3.55)
or:

(3.56)
Substituting equations 3.54 and 3.56 into equation 3.47 and rearranging gives:

(3.57)
or:

(3.58)
Similar to the derivation of MEA and DEA, the second term in the numerator of equation 3.58 represents the
concentration of CO2 which is in equilibrium with the bicarbonate and the hydroxide ions:

(3.59)
Equation 3.58 is a general rate expression for the reaction of CO2 with MDEA or any tertiary amine.
Depending on the magnitude of the second term of the denominator of this equation, one can obtain two limiting forms:

The rate expression in this case reduces to:

(3.60)
This form is essentially the expression, which would have been obtained if the second mechanism were used.
Many investigators including Haimor et al. (1987), Critchfield (1988), Tomcej et al. (1989), Little et al. (1990),
Rangwala et al. (1992), and Ko and Li (2000) adopted this form to fit the rate data of the CO2-MDEA system.
The rate constant of the reaction is given as a function of temperature by:

(3.61)
Comparison among the published values of the rate constant at 298.15 K shows a variation between 2.5 and 8.8
lit/mol/sec.

In this case the rate expression is given by:

(3.62)
Glasscock (1990) showed that this form reconciled the published rate data better.
He used activities instead of concentrations to obtain the rate constants. In the current study, the rate expression
represented by the first form (equation 3.60) with the rate constant reported by Critchfield (1988) will be used to model
the kinetics of the CO2 reaction with MDEA. The rate constant reported by Critchfield (1988) is given by:

(3.63)
2.3 CO2 Reaction with Blends of MEA-MDEA and DEA-MDEA
The absorption of CO2 in aqueous solution of blends of MEA-MDEA and DEA-MDEA was studied by Glasscock et
al. (1990), Versteeg et al. (1990), Rangwala et al. (1992), and Hagewiesche et al. (1995). Critchfield showed that the
interaction between MDEA and MEA is insignificant. Therefore the rate expressions (equation 3.37) for MEA and
(equation 3.60) for MDEA are still applicable for the mixture MEA-MDEA. However, for systems containing DEA and MDEA,
the latter acts as another base that neutralizes the zwitterion formed from the reaction of CO2 with DEA.
Hence, The CO2-DEA rate expression for systems containing DEA and MDEA should be corrected by adding the
contribution of MDEA to the neutralization of the zwitterion:
DEA/MDEA:

(3.64)

A value of 468 m6/kmol2/sec was reported in the thesis of Glasscock (1990) for the rate
constant k'R1R2R3N. In this work, this value will be used for
any temperature to compute the absorption rate of CO2in systems containing blends of DEA and MDEA.
Following the suggestion of Glasscock (1990), the effect of MDEA on the rate of reaction of CO2with MEA
will be ignored.
|
|
(3.27) |
Combining reactions 3.25 and 3.27 gives:
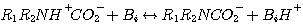
(3.28)
Comparing reactions 3.15 and 3.28 gives:
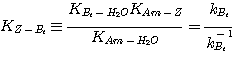
(3.29)
or:
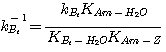
(3.30)
Adding reactions 3.14 and 3.15 and replacing with amine gives:

(3.31)
where:

(3.32)
or:

(3.33)
Substituting equations 3.24 and 3.33 into equation 3.30 gives:

(3.34)
Substituting equations 3.34 and 3.22 into equation 3.19 and rearranging gives:

(3.35)
The second term in the numerator of equation (3.35) represents the concentration of CO2 that is in is in
equilibrium with the amine, amine carbamate and protonated amine based on reaction 3.31. Hence, this equation can be
rewritten as:

(3.36)
As mentioned, the kinetics data for the CO2-MEA system follows a second order kinetics. Equation 3.35 is
reduced to
the second order form if the second term in the denominator is ignored in comparison to the first term, leading to:

(3.37)
The second order rate constant given by Hikita et al. 1977 will be used in this study to compute the CO2
absorption rate for systems containing MEA. This rate constant is expressed as a function of temperature by:
MEA:

(3.38)
In contrast, the first term in the denominator of equation (3.35) is negligible compared to the second term for the
CO2-DEA system:
DEA:

(3.39)
Equation 3.39 was used by Laddha and Danckwerts 1981, Blauwhoff et al. (1984), Versteeg and Van Swaaij (1988),
Critchfield (1988), and Glasscock (1990) to describe the kinetics data for the CO2-DEA system.
Glasscock (1990) assumed that the amine and the water are the only bases that contribute to the neutralization of the
zwitterion. The CO2-DEA rate expression reported by Glasscock 1990 will be utilized in this study.
This expression is given by
DEA:

(3.40)
The rate constants reported by Glasscock (1990) were extracted from the fit of the kinetics data and expressed as
functions of temperature according to

(3.41)

(3.42)
2.2 CO2 Reaction with MDEA
CO2 reacts indirectly with MDEA in the presence of water to form bicarbonate and protonated MDEA.
Three different mechanisms have been proposed for this reaction (Barth et al. 1981). The first mechanism suggests that
MDEA neutralizes the species formed by the CO2-water reactions (reactions 3.8 and 3.9). The second mechanism
assumes that MDEA associates with water before reacting with CO2:

(3.43)
The third mechanism follows the zwitterion mechanism described earlier for MEA and DEA:

(3.44)
The zwitterion formed immediately reacts with water and hydroxide to produce respectively bicarbonate and protonated
MDEA and bicarbonate and MDEA according to:
The third mechanism follows the zwitterion mechanism described earlier for MEA and DEA:

(3.45)

(3.46)
Adopting the third mechanism and following the procedure developed earlier for MEA and DEA, the following expression is
obtained for the rate of reaction of CO2 with MDEA:

(3.47)
Combining reactions 3.44 with 3.45 and 3.44 with 3.46 gives:

(3.48)

(3.49)
Reaction 3.48 can also be obtained from combinations of the following reactions:

(3.50)

(3.51)
Hence

(3.52)
Since reaction 3.50 is instantaneous, its products and reactants are at local equilibrium:

(3.53)
Therefore:

(3.54)
Reaction 3.49 can be obtained by combining the instantaneous water dissociation reaction (equation 2.1) with reaction
3.51 to obtain:

(3.55)
or:

(3.56)
Substituting equations 3.54 and 3.56 into equation 3.47 and rearranging gives:

(3.57)
or:

(3.58)
Similar to the derivation of MEA and DEA, the second term in the numerator of equation 3.58 represents the
concentration of CO2 which is in equilibrium with the bicarbonate and the hydroxide ions:

(3.59)
Equation 3.58 is a general rate expression for the reaction of CO2 with MDEA or any tertiary amine.
Depending on the magnitude of the second term of the denominator of this equation, one can obtain two limiting forms:

The rate expression in this case reduces to:

(3.60)
This form is essentially the expression, which would have been obtained if the second mechanism were used.
Many investigators including Haimor et al. (1987), Critchfield (1988), Tomcej et al. (1989), Little et al. (1990),
Rangwala et al. (1992), and Ko and Li (2000) adopted this form to fit the rate data of the CO2-MDEA system.
The rate constant of the reaction is given as a function of temperature by:

(3.61)
Comparison among the published values of the rate constant at 298.15 K shows a variation between 2.5 and 8.8
lit/mol/sec.

In this case the rate expression is given by:

(3.62)
Glasscock (1990) showed that this form reconciled the published rate data better.
He used activities instead of concentrations to obtain the rate constants. In the current study, the rate expression
represented by the first form (equation 3.60) with the rate constant reported by Critchfield (1988) will be used to model
the kinetics of the CO2 reaction with MDEA. The rate constant reported by Critchfield (1988) is given by:

(3.63)
2.3 CO2 Reaction with Blends of MEA-MDEA and DEA-MDEA
The absorption of CO2 in aqueous solution of blends of MEA-MDEA and DEA-MDEA was studied by Glasscock et
al. (1990), Versteeg et al. (1990), Rangwala et al. (1992), and Hagewiesche et al. (1995). Critchfield showed that the
interaction between MDEA and MEA is insignificant. Therefore the rate expressions (equation 3.37) for MEA and
(equation 3.60) for MDEA are still applicable for the mixture MEA-MDEA. However, for systems containing DEA and MDEA,
the latter acts as another base that neutralizes the zwitterion formed from the reaction of CO2 with DEA.
Hence, The CO2-DEA rate expression for systems containing DEA and MDEA should be corrected by adding the
contribution of MDEA to the neutralization of the zwitterion:
DEA/MDEA:

(3.64)

A value of 468 m6/kmol2/sec was reported in the thesis of Glasscock (1990) for the rate
constant k'R1R2R3N. In this work, this value will be used for
any temperature to compute the absorption rate of CO2in systems containing blends of DEA and MDEA.
Following the suggestion of Glasscock (1990), the effect of MDEA on the rate of reaction of CO2with MEA
will be ignored.
|
|
(3.28) |
Comparing reactions 3.15 and 3.28 gives:
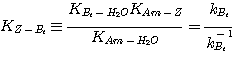
(3.29)
or:
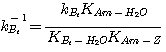
(3.30)
Adding reactions 3.14 and 3.15 and replacing with amine gives:

(3.31)
where:

(3.32)
or:

(3.33)
Substituting equations 3.24 and 3.33 into equation 3.30 gives:

(3.34)
Substituting equations 3.34 and 3.22 into equation 3.19 and rearranging gives:

(3.35)
The second term in the numerator of equation (3.35) represents the concentration of CO2 that is in is in
equilibrium with the amine, amine carbamate and protonated amine based on reaction 3.31. Hence, this equation can be
rewritten as:

(3.36)
As mentioned, the kinetics data for the CO2-MEA system follows a second order kinetics. Equation 3.35 is
reduced to
the second order form if the second term in the denominator is ignored in comparison to the first term, leading to:

(3.37)
The second order rate constant given by Hikita et al. 1977 will be used in this study to compute the CO2
absorption rate for systems containing MEA. This rate constant is expressed as a function of temperature by:
MEA:

(3.38)
In contrast, the first term in the denominator of equation (3.35) is negligible compared to the second term for the
CO2-DEA system:
DEA:

(3.39)
Equation 3.39 was used by Laddha and Danckwerts 1981, Blauwhoff et al. (1984), Versteeg and Van Swaaij (1988),
Critchfield (1988), and Glasscock (1990) to describe the kinetics data for the CO2-DEA system.
Glasscock (1990) assumed that the amine and the water are the only bases that contribute to the neutralization of the
zwitterion. The CO2-DEA rate expression reported by Glasscock 1990 will be utilized in this study.
This expression is given by
DEA:

(3.40)
The rate constants reported by Glasscock (1990) were extracted from the fit of the kinetics data and expressed as
functions of temperature according to

(3.41)

(3.42)
2.2 CO2 Reaction with MDEA
CO2 reacts indirectly with MDEA in the presence of water to form bicarbonate and protonated MDEA.
Three different mechanisms have been proposed for this reaction (Barth et al. 1981). The first mechanism suggests that
MDEA neutralizes the species formed by the CO2-water reactions (reactions 3.8 and 3.9). The second mechanism
assumes that MDEA associates with water before reacting with CO2:

(3.43)
The third mechanism follows the zwitterion mechanism described earlier for MEA and DEA:

(3.44)
The zwitterion formed immediately reacts with water and hydroxide to produce respectively bicarbonate and protonated
MDEA and bicarbonate and MDEA according to:
The third mechanism follows the zwitterion mechanism described earlier for MEA and DEA:

(3.45)

(3.46)
Adopting the third mechanism and following the procedure developed earlier for MEA and DEA, the following expression is
obtained for the rate of reaction of CO2 with MDEA:

(3.47)
Combining reactions 3.44 with 3.45 and 3.44 with 3.46 gives:

(3.48)

(3.49)
Reaction 3.48 can also be obtained from combinations of the following reactions:

(3.50)

(3.51)
Hence

(3.52)
Since reaction 3.50 is instantaneous, its products and reactants are at local equilibrium:

(3.53)
Therefore:

(3.54)
Reaction 3.49 can be obtained by combining the instantaneous water dissociation reaction (equation 2.1) with reaction
3.51 to obtain:

(3.55)
or:

(3.56)
Substituting equations 3.54 and 3.56 into equation 3.47 and rearranging gives:

(3.57)
or:

(3.58)
Similar to the derivation of MEA and DEA, the second term in the numerator of equation 3.58 represents the
concentration of CO2 which is in equilibrium with the bicarbonate and the hydroxide ions:

(3.59)
Equation 3.58 is a general rate expression for the reaction of CO2 with MDEA or any tertiary amine.
Depending on the magnitude of the second term of the denominator of this equation, one can obtain two limiting forms:

The rate expression in this case reduces to:

(3.60)
This form is essentially the expression, which would have been obtained if the second mechanism were used.
Many investigators including Haimor et al. (1987), Critchfield (1988), Tomcej et al. (1989), Little et al. (1990),
Rangwala et al. (1992), and Ko and Li (2000) adopted this form to fit the rate data of the CO2-MDEA system.
The rate constant of the reaction is given as a function of temperature by:

(3.61)
Comparison among the published values of the rate constant at 298.15 K shows a variation between 2.5 and 8.8
lit/mol/sec.

In this case the rate expression is given by:

(3.62)
Glasscock (1990) showed that this form reconciled the published rate data better.
He used activities instead of concentrations to obtain the rate constants. In the current study, the rate expression
represented by the first form (equation 3.60) with the rate constant reported by Critchfield (1988) will be used to model
the kinetics of the CO2 reaction with MDEA. The rate constant reported by Critchfield (1988) is given by:

(3.63)
2.3 CO2 Reaction with Blends of MEA-MDEA and DEA-MDEA
The absorption of CO2 in aqueous solution of blends of MEA-MDEA and DEA-MDEA was studied by Glasscock et
al. (1990), Versteeg et al. (1990), Rangwala et al. (1992), and Hagewiesche et al. (1995). Critchfield showed that the
interaction between MDEA and MEA is insignificant. Therefore the rate expressions (equation 3.37) for MEA and
(equation 3.60) for MDEA are still applicable for the mixture MEA-MDEA. However, for systems containing DEA and MDEA,
the latter acts as another base that neutralizes the zwitterion formed from the reaction of CO2 with DEA.
Hence, The CO2-DEA rate expression for systems containing DEA and MDEA should be corrected by adding the
contribution of MDEA to the neutralization of the zwitterion:
DEA/MDEA:

(3.64)

A value of 468 m6/kmol2/sec was reported in the thesis of Glasscock (1990) for the rate
constant k'R1R2R3N. In this work, this value will be used for
any temperature to compute the absorption rate of CO2in systems containing blends of DEA and MDEA.
Following the suggestion of Glasscock (1990), the effect of MDEA on the rate of reaction of CO2with MEA
will be ignored.
|
|
(3.29) |
or:
|
|
(3.30) |
Adding reactions 3.14 and 3.15 and replacing with amine gives:

(3.31)
where:

(3.32)
or:

(3.33)
Substituting equations 3.24 and 3.33 into equation 3.30 gives:

(3.34)
Substituting equations 3.34 and 3.22 into equation 3.19 and rearranging gives:

(3.35)
The second term in the numerator of equation (3.35) represents the concentration of CO2 that is in is in
equilibrium with the amine, amine carbamate and protonated amine based on reaction 3.31. Hence, this equation can be
rewritten as:

(3.36)
As mentioned, the kinetics data for the CO2-MEA system follows a second order kinetics. Equation 3.35 is
reduced to
the second order form if the second term in the denominator is ignored in comparison to the first term, leading to:

(3.37)
The second order rate constant given by Hikita et al. 1977 will be used in this study to compute the CO2
absorption rate for systems containing MEA. This rate constant is expressed as a function of temperature by:
MEA:

(3.38)
In contrast, the first term in the denominator of equation (3.35) is negligible compared to the second term for the
CO2-DEA system:
DEA:

(3.39)
Equation 3.39 was used by Laddha and Danckwerts 1981, Blauwhoff et al. (1984), Versteeg and Van Swaaij (1988),
Critchfield (1988), and Glasscock (1990) to describe the kinetics data for the CO2-DEA system.
Glasscock (1990) assumed that the amine and the water are the only bases that contribute to the neutralization of the
zwitterion. The CO2-DEA rate expression reported by Glasscock 1990 will be utilized in this study.
This expression is given by
DEA:

(3.40)
The rate constants reported by Glasscock (1990) were extracted from the fit of the kinetics data and expressed as
functions of temperature according to

(3.41)

(3.42)
2.2 CO2 Reaction with MDEA
CO2 reacts indirectly with MDEA in the presence of water to form bicarbonate and protonated MDEA.
Three different mechanisms have been proposed for this reaction (Barth et al. 1981). The first mechanism suggests that
MDEA neutralizes the species formed by the CO2-water reactions (reactions 3.8 and 3.9). The second mechanism
assumes that MDEA associates with water before reacting with CO2:

(3.43)
The third mechanism follows the zwitterion mechanism described earlier for MEA and DEA:

(3.44)
The zwitterion formed immediately reacts with water and hydroxide to produce respectively bicarbonate and protonated
MDEA and bicarbonate and MDEA according to:
The third mechanism follows the zwitterion mechanism described earlier for MEA and DEA:

(3.45)

(3.46)
Adopting the third mechanism and following the procedure developed earlier for MEA and DEA, the following expression is
obtained for the rate of reaction of CO2 with MDEA:

(3.47)
Combining reactions 3.44 with 3.45 and 3.44 with 3.46 gives:

(3.48)

(3.49)
Reaction 3.48 can also be obtained from combinations of the following reactions:

(3.50)

(3.51)
Hence

(3.52)
Since reaction 3.50 is instantaneous, its products and reactants are at local equilibrium:

(3.53)
Therefore:

(3.54)
Reaction 3.49 can be obtained by combining the instantaneous water dissociation reaction (equation 2.1) with reaction
3.51 to obtain:

(3.55)
or:

(3.56)
Substituting equations 3.54 and 3.56 into equation 3.47 and rearranging gives:

(3.57)
or:

(3.58)
Similar to the derivation of MEA and DEA, the second term in the numerator of equation 3.58 represents the
concentration of CO2 which is in equilibrium with the bicarbonate and the hydroxide ions:

(3.59)
Equation 3.58 is a general rate expression for the reaction of CO2 with MDEA or any tertiary amine.
Depending on the magnitude of the second term of the denominator of this equation, one can obtain two limiting forms:

The rate expression in this case reduces to:

(3.60)
This form is essentially the expression, which would have been obtained if the second mechanism were used.
Many investigators including Haimor et al. (1987), Critchfield (1988), Tomcej et al. (1989), Little et al. (1990),
Rangwala et al. (1992), and Ko and Li (2000) adopted this form to fit the rate data of the CO2-MDEA system.
The rate constant of the reaction is given as a function of temperature by:

(3.61)
Comparison among the published values of the rate constant at 298.15 K shows a variation between 2.5 and 8.8
lit/mol/sec.

In this case the rate expression is given by:

(3.62)
Glasscock (1990) showed that this form reconciled the published rate data better.
He used activities instead of concentrations to obtain the rate constants. In the current study, the rate expression
represented by the first form (equation 3.60) with the rate constant reported by Critchfield (1988) will be used to model
the kinetics of the CO2 reaction with MDEA. The rate constant reported by Critchfield (1988) is given by:

(3.63)
2.3 CO2 Reaction with Blends of MEA-MDEA and DEA-MDEA
The absorption of CO2 in aqueous solution of blends of MEA-MDEA and DEA-MDEA was studied by Glasscock et
al. (1990), Versteeg et al. (1990), Rangwala et al. (1992), and Hagewiesche et al. (1995). Critchfield showed that the
interaction between MDEA and MEA is insignificant. Therefore the rate expressions (equation 3.37) for MEA and
(equation 3.60) for MDEA are still applicable for the mixture MEA-MDEA. However, for systems containing DEA and MDEA,
the latter acts as another base that neutralizes the zwitterion formed from the reaction of CO2 with DEA.
Hence, The CO2-DEA rate expression for systems containing DEA and MDEA should be corrected by adding the
contribution of MDEA to the neutralization of the zwitterion:
DEA/MDEA:

(3.64)

A value of 468 m6/kmol2/sec was reported in the thesis of Glasscock (1990) for the rate
constant k'R1R2R3N. In this work, this value will be used for
any temperature to compute the absorption rate of CO2in systems containing blends of DEA and MDEA.
Following the suggestion of Glasscock (1990), the effect of MDEA on the rate of reaction of CO2with MEA
will be ignored.
|
|
(3.31) |
where:
|
|
(3.32) |
or:
|
|
(3.33) |
Substituting equations 3.24 and 3.33 into equation 3.30 gives:

(3.34)
Substituting equations 3.34 and 3.22 into equation 3.19 and rearranging gives:

(3.35)
The second term in the numerator of equation (3.35) represents the concentration of CO2 that is in is in
equilibrium with the amine, amine carbamate and protonated amine based on reaction 3.31. Hence, this equation can be
rewritten as:

(3.36)
As mentioned, the kinetics data for the CO2-MEA system follows a second order kinetics. Equation 3.35 is
reduced to
the second order form if the second term in the denominator is ignored in comparison to the first term, leading to:

(3.37)
The second order rate constant given by Hikita et al. 1977 will be used in this study to compute the CO2
absorption rate for systems containing MEA. This rate constant is expressed as a function of temperature by:
MEA:

(3.38)
In contrast, the first term in the denominator of equation (3.35) is negligible compared to the second term for the
CO2-DEA system:
DEA:

(3.39)
Equation 3.39 was used by Laddha and Danckwerts 1981, Blauwhoff et al. (1984), Versteeg and Van Swaaij (1988),
Critchfield (1988), and Glasscock (1990) to describe the kinetics data for the CO2-DEA system.
Glasscock (1990) assumed that the amine and the water are the only bases that contribute to the neutralization of the
zwitterion. The CO2-DEA rate expression reported by Glasscock 1990 will be utilized in this study.
This expression is given by
DEA:

(3.40)
The rate constants reported by Glasscock (1990) were extracted from the fit of the kinetics data and expressed as
functions of temperature according to

(3.41)

(3.42)
2.2 CO2 Reaction with MDEA
CO2 reacts indirectly with MDEA in the presence of water to form bicarbonate and protonated MDEA.
Three different mechanisms have been proposed for this reaction (Barth et al. 1981). The first mechanism suggests that
MDEA neutralizes the species formed by the CO2-water reactions (reactions 3.8 and 3.9). The second mechanism
assumes that MDEA associates with water before reacting with CO2:

(3.43)
The third mechanism follows the zwitterion mechanism described earlier for MEA and DEA:

(3.44)
The zwitterion formed immediately reacts with water and hydroxide to produce respectively bicarbonate and protonated
MDEA and bicarbonate and MDEA according to:
The third mechanism follows the zwitterion mechanism described earlier for MEA and DEA:

(3.45)

(3.46)
Adopting the third mechanism and following the procedure developed earlier for MEA and DEA, the following expression is
obtained for the rate of reaction of CO2 with MDEA:

(3.47)
Combining reactions 3.44 with 3.45 and 3.44 with 3.46 gives:

(3.48)

(3.49)
Reaction 3.48 can also be obtained from combinations of the following reactions:

(3.50)

(3.51)
Hence

(3.52)
Since reaction 3.50 is instantaneous, its products and reactants are at local equilibrium:

(3.53)
Therefore:

(3.54)
Reaction 3.49 can be obtained by combining the instantaneous water dissociation reaction (equation 2.1) with reaction
3.51 to obtain:

(3.55)
or:

(3.56)
Substituting equations 3.54 and 3.56 into equation 3.47 and rearranging gives:

(3.57)
or:

(3.58)
Similar to the derivation of MEA and DEA, the second term in the numerator of equation 3.58 represents the
concentration of CO2 which is in equilibrium with the bicarbonate and the hydroxide ions:

(3.59)
Equation 3.58 is a general rate expression for the reaction of CO2 with MDEA or any tertiary amine.
Depending on the magnitude of the second term of the denominator of this equation, one can obtain two limiting forms:

The rate expression in this case reduces to:

(3.60)
This form is essentially the expression, which would have been obtained if the second mechanism were used.
Many investigators including Haimor et al. (1987), Critchfield (1988), Tomcej et al. (1989), Little et al. (1990),
Rangwala et al. (1992), and Ko and Li (2000) adopted this form to fit the rate data of the CO2-MDEA system.
The rate constant of the reaction is given as a function of temperature by:

(3.61)
Comparison among the published values of the rate constant at 298.15 K shows a variation between 2.5 and 8.8
lit/mol/sec.

In this case the rate expression is given by:

(3.62)
Glasscock (1990) showed that this form reconciled the published rate data better.
He used activities instead of concentrations to obtain the rate constants. In the current study, the rate expression
represented by the first form (equation 3.60) with the rate constant reported by Critchfield (1988) will be used to model
the kinetics of the CO2 reaction with MDEA. The rate constant reported by Critchfield (1988) is given by:

(3.63)
2.3 CO2 Reaction with Blends of MEA-MDEA and DEA-MDEA
The absorption of CO2 in aqueous solution of blends of MEA-MDEA and DEA-MDEA was studied by Glasscock et
al. (1990), Versteeg et al. (1990), Rangwala et al. (1992), and Hagewiesche et al. (1995). Critchfield showed that the
interaction between MDEA and MEA is insignificant. Therefore the rate expressions (equation 3.37) for MEA and
(equation 3.60) for MDEA are still applicable for the mixture MEA-MDEA. However, for systems containing DEA and MDEA,
the latter acts as another base that neutralizes the zwitterion formed from the reaction of CO2 with DEA.
Hence, The CO2-DEA rate expression for systems containing DEA and MDEA should be corrected by adding the
contribution of MDEA to the neutralization of the zwitterion:
DEA/MDEA:

(3.64)

A value of 468 m6/kmol2/sec was reported in the thesis of Glasscock (1990) for the rate
constant k'R1R2R3N. In this work, this value will be used for
any temperature to compute the absorption rate of CO2in systems containing blends of DEA and MDEA.
Following the suggestion of Glasscock (1990), the effect of MDEA on the rate of reaction of CO2with MEA
will be ignored.
|
|
(3.34) |
Substituting equations 3.34 and 3.22 into equation 3.19 and rearranging gives:

(3.35)
The second term in the numerator of equation (3.35) represents the concentration of CO2 that is in is in
equilibrium with the amine, amine carbamate and protonated amine based on reaction 3.31. Hence, this equation can be
rewritten as:

(3.36)
As mentioned, the kinetics data for the CO2-MEA system follows a second order kinetics. Equation 3.35 is
reduced to
the second order form if the second term in the denominator is ignored in comparison to the first term, leading to:

(3.37)
The second order rate constant given by Hikita et al. 1977 will be used in this study to compute the CO2
absorption rate for systems containing MEA. This rate constant is expressed as a function of temperature by:
MEA:

(3.38)
In contrast, the first term in the denominator of equation (3.35) is negligible compared to the second term for the
CO2-DEA system:
DEA:

(3.39)
Equation 3.39 was used by Laddha and Danckwerts 1981, Blauwhoff et al. (1984), Versteeg and Van Swaaij (1988),
Critchfield (1988), and Glasscock (1990) to describe the kinetics data for the CO2-DEA system.
Glasscock (1990) assumed that the amine and the water are the only bases that contribute to the neutralization of the
zwitterion. The CO2-DEA rate expression reported by Glasscock 1990 will be utilized in this study.
This expression is given by
DEA:

(3.40)
The rate constants reported by Glasscock (1990) were extracted from the fit of the kinetics data and expressed as
functions of temperature according to

(3.41)

(3.42)
2.2 CO2 Reaction with MDEA
CO2 reacts indirectly with MDEA in the presence of water to form bicarbonate and protonated MDEA.
Three different mechanisms have been proposed for this reaction (Barth et al. 1981). The first mechanism suggests that
MDEA neutralizes the species formed by the CO2-water reactions (reactions 3.8 and 3.9). The second mechanism
assumes that MDEA associates with water before reacting with CO2:

(3.43)
The third mechanism follows the zwitterion mechanism described earlier for MEA and DEA:

(3.44)
The zwitterion formed immediately reacts with water and hydroxide to produce respectively bicarbonate and protonated
MDEA and bicarbonate and MDEA according to:
The third mechanism follows the zwitterion mechanism described earlier for MEA and DEA:

(3.45)

(3.46)
Adopting the third mechanism and following the procedure developed earlier for MEA and DEA, the following expression is
obtained for the rate of reaction of CO2 with MDEA:

(3.47)
Combining reactions 3.44 with 3.45 and 3.44 with 3.46 gives:

(3.48)

(3.49)
Reaction 3.48 can also be obtained from combinations of the following reactions:

(3.50)

(3.51)
Hence

(3.52)
Since reaction 3.50 is instantaneous, its products and reactants are at local equilibrium:

(3.53)
Therefore:

(3.54)
Reaction 3.49 can be obtained by combining the instantaneous water dissociation reaction (equation 2.1) with reaction
3.51 to obtain:

(3.55)
or:

(3.56)
Substituting equations 3.54 and 3.56 into equation 3.47 and rearranging gives:

(3.57)
or:

(3.58)
Similar to the derivation of MEA and DEA, the second term in the numerator of equation 3.58 represents the
concentration of CO2 which is in equilibrium with the bicarbonate and the hydroxide ions:

(3.59)
Equation 3.58 is a general rate expression for the reaction of CO2 with MDEA or any tertiary amine.
Depending on the magnitude of the second term of the denominator of this equation, one can obtain two limiting forms:

The rate expression in this case reduces to:

(3.60)
This form is essentially the expression, which would have been obtained if the second mechanism were used.
Many investigators including Haimor et al. (1987), Critchfield (1988), Tomcej et al. (1989), Little et al. (1990),
Rangwala et al. (1992), and Ko and Li (2000) adopted this form to fit the rate data of the CO2-MDEA system.
The rate constant of the reaction is given as a function of temperature by:

(3.61)
Comparison among the published values of the rate constant at 298.15 K shows a variation between 2.5 and 8.8
lit/mol/sec.

In this case the rate expression is given by:

(3.62)
Glasscock (1990) showed that this form reconciled the published rate data better.
He used activities instead of concentrations to obtain the rate constants. In the current study, the rate expression
represented by the first form (equation 3.60) with the rate constant reported by Critchfield (1988) will be used to model
the kinetics of the CO2 reaction with MDEA. The rate constant reported by Critchfield (1988) is given by:

(3.63)
2.3 CO2 Reaction with Blends of MEA-MDEA and DEA-MDEA
The absorption of CO2 in aqueous solution of blends of MEA-MDEA and DEA-MDEA was studied by Glasscock et
al. (1990), Versteeg et al. (1990), Rangwala et al. (1992), and Hagewiesche et al. (1995). Critchfield showed that the
interaction between MDEA and MEA is insignificant. Therefore the rate expressions (equation 3.37) for MEA and
(equation 3.60) for MDEA are still applicable for the mixture MEA-MDEA. However, for systems containing DEA and MDEA,
the latter acts as another base that neutralizes the zwitterion formed from the reaction of CO2 with DEA.
Hence, The CO2-DEA rate expression for systems containing DEA and MDEA should be corrected by adding the
contribution of MDEA to the neutralization of the zwitterion:
DEA/MDEA:

(3.64)

A value of 468 m6/kmol2/sec was reported in the thesis of Glasscock (1990) for the rate
constant k'R1R2R3N. In this work, this value will be used for
any temperature to compute the absorption rate of CO2in systems containing blends of DEA and MDEA.
Following the suggestion of Glasscock (1990), the effect of MDEA on the rate of reaction of CO2with MEA
will be ignored.
|
|
(3.35) |
The second term in the numerator of equation (3.35) represents the concentration of CO2 that is in is in
equilibrium with the amine, amine carbamate and protonated amine based on reaction 3.31. Hence, this equation can be
rewritten as:

(3.36)
As mentioned, the kinetics data for the CO2-MEA system follows a second order kinetics. Equation 3.35 is
reduced to
the second order form if the second term in the denominator is ignored in comparison to the first term, leading to:

(3.37)
The second order rate constant given by Hikita et al. 1977 will be used in this study to compute the CO2
absorption rate for systems containing MEA. This rate constant is expressed as a function of temperature by:
MEA:

(3.38)
In contrast, the first term in the denominator of equation (3.35) is negligible compared to the second term for the
CO2-DEA system:
DEA:

(3.39)
Equation 3.39 was used by Laddha and Danckwerts 1981, Blauwhoff et al. (1984), Versteeg and Van Swaaij (1988),
Critchfield (1988), and Glasscock (1990) to describe the kinetics data for the CO2-DEA system.
Glasscock (1990) assumed that the amine and the water are the only bases that contribute to the neutralization of the
zwitterion. The CO2-DEA rate expression reported by Glasscock 1990 will be utilized in this study.
This expression is given by
DEA:

(3.40)
The rate constants reported by Glasscock (1990) were extracted from the fit of the kinetics data and expressed as
functions of temperature according to

(3.41)

(3.42)
2.2 CO2 Reaction with MDEA
CO2 reacts indirectly with MDEA in the presence of water to form bicarbonate and protonated MDEA.
Three different mechanisms have been proposed for this reaction (Barth et al. 1981). The first mechanism suggests that
MDEA neutralizes the species formed by the CO2-water reactions (reactions 3.8 and 3.9). The second mechanism
assumes that MDEA associates with water before reacting with CO2:

(3.43)
The third mechanism follows the zwitterion mechanism described earlier for MEA and DEA:

(3.44)
The zwitterion formed immediately reacts with water and hydroxide to produce respectively bicarbonate and protonated
MDEA and bicarbonate and MDEA according to:
The third mechanism follows the zwitterion mechanism described earlier for MEA and DEA:

(3.45)

(3.46)
Adopting the third mechanism and following the procedure developed earlier for MEA and DEA, the following expression is
obtained for the rate of reaction of CO2 with MDEA:

(3.47)
Combining reactions 3.44 with 3.45 and 3.44 with 3.46 gives:

(3.48)

(3.49)
Reaction 3.48 can also be obtained from combinations of the following reactions:

(3.50)

(3.51)
Hence

(3.52)
Since reaction 3.50 is instantaneous, its products and reactants are at local equilibrium:

(3.53)
Therefore:

(3.54)
Reaction 3.49 can be obtained by combining the instantaneous water dissociation reaction (equation 2.1) with reaction
3.51 to obtain:

(3.55)
or:

(3.56)
Substituting equations 3.54 and 3.56 into equation 3.47 and rearranging gives:

(3.57)
or:

(3.58)
Similar to the derivation of MEA and DEA, the second term in the numerator of equation 3.58 represents the
concentration of CO2 which is in equilibrium with the bicarbonate and the hydroxide ions:

(3.59)
Equation 3.58 is a general rate expression for the reaction of CO2 with MDEA or any tertiary amine.
Depending on the magnitude of the second term of the denominator of this equation, one can obtain two limiting forms:

The rate expression in this case reduces to:

(3.60)
This form is essentially the expression, which would have been obtained if the second mechanism were used.
Many investigators including Haimor et al. (1987), Critchfield (1988), Tomcej et al. (1989), Little et al. (1990),
Rangwala et al. (1992), and Ko and Li (2000) adopted this form to fit the rate data of the CO2-MDEA system.
The rate constant of the reaction is given as a function of temperature by:

(3.61)
Comparison among the published values of the rate constant at 298.15 K shows a variation between 2.5 and 8.8
lit/mol/sec.

In this case the rate expression is given by:

(3.62)
Glasscock (1990) showed that this form reconciled the published rate data better.
He used activities instead of concentrations to obtain the rate constants. In the current study, the rate expression
represented by the first form (equation 3.60) with the rate constant reported by Critchfield (1988) will be used to model
the kinetics of the CO2 reaction with MDEA. The rate constant reported by Critchfield (1988) is given by:

(3.63)
2.3 CO2 Reaction with Blends of MEA-MDEA and DEA-MDEA
The absorption of CO2 in aqueous solution of blends of MEA-MDEA and DEA-MDEA was studied by Glasscock et
al. (1990), Versteeg et al. (1990), Rangwala et al. (1992), and Hagewiesche et al. (1995). Critchfield showed that the
interaction between MDEA and MEA is insignificant. Therefore the rate expressions (equation 3.37) for MEA and
(equation 3.60) for MDEA are still applicable for the mixture MEA-MDEA. However, for systems containing DEA and MDEA,
the latter acts as another base that neutralizes the zwitterion formed from the reaction of CO2 with DEA.
Hence, The CO2-DEA rate expression for systems containing DEA and MDEA should be corrected by adding the
contribution of MDEA to the neutralization of the zwitterion:
DEA/MDEA:

(3.64)

A value of 468 m6/kmol2/sec was reported in the thesis of Glasscock (1990) for the rate
constant k'R1R2R3N. In this work, this value will be used for
any temperature to compute the absorption rate of CO2in systems containing blends of DEA and MDEA.
Following the suggestion of Glasscock (1990), the effect of MDEA on the rate of reaction of CO2with MEA
will be ignored.
|
|
(3.36) |
As mentioned, the kinetics data for the CO2-MEA system follows a second order kinetics. Equation 3.35 is
reduced to
the second order form if the second term in the denominator is ignored in comparison to the first term, leading to:

(3.37)
The second order rate constant given by Hikita et al. 1977 will be used in this study to compute the CO2
absorption rate for systems containing MEA. This rate constant is expressed as a function of temperature by:
MEA:

(3.38)
In contrast, the first term in the denominator of equation (3.35) is negligible compared to the second term for the
CO2-DEA system:
DEA:

(3.39)
Equation 3.39 was used by Laddha and Danckwerts 1981, Blauwhoff et al. (1984), Versteeg and Van Swaaij (1988),
Critchfield (1988), and Glasscock (1990) to describe the kinetics data for the CO2-DEA system.
Glasscock (1990) assumed that the amine and the water are the only bases that contribute to the neutralization of the
zwitterion. The CO2-DEA rate expression reported by Glasscock 1990 will be utilized in this study.
This expression is given by
DEA:

(3.40)
The rate constants reported by Glasscock (1990) were extracted from the fit of the kinetics data and expressed as
functions of temperature according to

(3.41)

(3.42)
2.2 CO2 Reaction with MDEA
CO2 reacts indirectly with MDEA in the presence of water to form bicarbonate and protonated MDEA.
Three different mechanisms have been proposed for this reaction (Barth et al. 1981). The first mechanism suggests that
MDEA neutralizes the species formed by the CO2-water reactions (reactions 3.8 and 3.9). The second mechanism
assumes that MDEA associates with water before reacting with CO2:

(3.43)
The third mechanism follows the zwitterion mechanism described earlier for MEA and DEA:

(3.44)
The zwitterion formed immediately reacts with water and hydroxide to produce respectively bicarbonate and protonated
MDEA and bicarbonate and MDEA according to:
The third mechanism follows the zwitterion mechanism described earlier for MEA and DEA:

(3.45)

(3.46)
Adopting the third mechanism and following the procedure developed earlier for MEA and DEA, the following expression is
obtained for the rate of reaction of CO2 with MDEA:

(3.47)
Combining reactions 3.44 with 3.45 and 3.44 with 3.46 gives:

(3.48)

(3.49)
Reaction 3.48 can also be obtained from combinations of the following reactions:

(3.50)

(3.51)
Hence

(3.52)
Since reaction 3.50 is instantaneous, its products and reactants are at local equilibrium:

(3.53)
Therefore:

(3.54)
Reaction 3.49 can be obtained by combining the instantaneous water dissociation reaction (equation 2.1) with reaction
3.51 to obtain:

(3.55)
or:

(3.56)
Substituting equations 3.54 and 3.56 into equation 3.47 and rearranging gives:

(3.57)
or:

(3.58)
Similar to the derivation of MEA and DEA, the second term in the numerator of equation 3.58 represents the
concentration of CO2 which is in equilibrium with the bicarbonate and the hydroxide ions:

(3.59)
Equation 3.58 is a general rate expression for the reaction of CO2 with MDEA or any tertiary amine.
Depending on the magnitude of the second term of the denominator of this equation, one can obtain two limiting forms:

The rate expression in this case reduces to:

(3.60)
This form is essentially the expression, which would have been obtained if the second mechanism were used.
Many investigators including Haimor et al. (1987), Critchfield (1988), Tomcej et al. (1989), Little et al. (1990),
Rangwala et al. (1992), and Ko and Li (2000) adopted this form to fit the rate data of the CO2-MDEA system.
The rate constant of the reaction is given as a function of temperature by:

(3.61)
Comparison among the published values of the rate constant at 298.15 K shows a variation between 2.5 and 8.8
lit/mol/sec.

In this case the rate expression is given by:

(3.62)
Glasscock (1990) showed that this form reconciled the published rate data better.
He used activities instead of concentrations to obtain the rate constants. In the current study, the rate expression
represented by the first form (equation 3.60) with the rate constant reported by Critchfield (1988) will be used to model
the kinetics of the CO2 reaction with MDEA. The rate constant reported by Critchfield (1988) is given by:

(3.63)
2.3 CO2 Reaction with Blends of MEA-MDEA and DEA-MDEA
The absorption of CO2 in aqueous solution of blends of MEA-MDEA and DEA-MDEA was studied by Glasscock et
al. (1990), Versteeg et al. (1990), Rangwala et al. (1992), and Hagewiesche et al. (1995). Critchfield showed that the
interaction between MDEA and MEA is insignificant. Therefore the rate expressions (equation 3.37) for MEA and
(equation 3.60) for MDEA are still applicable for the mixture MEA-MDEA. However, for systems containing DEA and MDEA,
the latter acts as another base that neutralizes the zwitterion formed from the reaction of CO2 with DEA.
Hence, The CO2-DEA rate expression for systems containing DEA and MDEA should be corrected by adding the
contribution of MDEA to the neutralization of the zwitterion:
DEA/MDEA:

(3.64)

A value of 468 m6/kmol2/sec was reported in the thesis of Glasscock (1990) for the rate
constant k'R1R2R3N. In this work, this value will be used for
any temperature to compute the absorption rate of CO2in systems containing blends of DEA and MDEA.
Following the suggestion of Glasscock (1990), the effect of MDEA on the rate of reaction of CO2with MEA
will be ignored.
|
|
(3.37) |
The second order rate constant given by Hikita et al. 1977 will be used in this study to compute the CO2
absorption rate for systems containing MEA. This rate constant is expressed as a function of temperature by:
MEA:

(3.38)
In contrast, the first term in the denominator of equation (3.35) is negligible compared to the second term for the
CO2-DEA system:
DEA:

(3.39)
Equation 3.39 was used by Laddha and Danckwerts 1981, Blauwhoff et al. (1984), Versteeg and Van Swaaij (1988),
Critchfield (1988), and Glasscock (1990) to describe the kinetics data for the CO2-DEA system.
Glasscock (1990) assumed that the amine and the water are the only bases that contribute to the neutralization of the
zwitterion. The CO2-DEA rate expression reported by Glasscock 1990 will be utilized in this study.
This expression is given by
DEA:

(3.40)
The rate constants reported by Glasscock (1990) were extracted from the fit of the kinetics data and expressed as
functions of temperature according to

(3.41)

(3.42)
2.2 CO2 Reaction with MDEA
CO2 reacts indirectly with MDEA in the presence of water to form bicarbonate and protonated MDEA.
Three different mechanisms have been proposed for this reaction (Barth et al. 1981). The first mechanism suggests that
MDEA neutralizes the species formed by the CO2-water reactions (reactions 3.8 and 3.9). The second mechanism
assumes that MDEA associates with water before reacting with CO2:

(3.43)
The third mechanism follows the zwitterion mechanism described earlier for MEA and DEA:

(3.44)
The zwitterion formed immediately reacts with water and hydroxide to produce respectively bicarbonate and protonated
MDEA and bicarbonate and MDEA according to:
The third mechanism follows the zwitterion mechanism described earlier for MEA and DEA:

(3.45)

(3.46)
Adopting the third mechanism and following the procedure developed earlier for MEA and DEA, the following expression is
obtained for the rate of reaction of CO2 with MDEA:

(3.47)
Combining reactions 3.44 with 3.45 and 3.44 with 3.46 gives:

(3.48)

(3.49)
Reaction 3.48 can also be obtained from combinations of the following reactions:

(3.50)

(3.51)
Hence

(3.52)
Since reaction 3.50 is instantaneous, its products and reactants are at local equilibrium:

(3.53)
Therefore:

(3.54)
Reaction 3.49 can be obtained by combining the instantaneous water dissociation reaction (equation 2.1) with reaction
3.51 to obtain:

(3.55)
or:

(3.56)
Substituting equations 3.54 and 3.56 into equation 3.47 and rearranging gives:

(3.57)
or:

(3.58)
Similar to the derivation of MEA and DEA, the second term in the numerator of equation 3.58 represents the
concentration of CO2 which is in equilibrium with the bicarbonate and the hydroxide ions:

(3.59)
Equation 3.58 is a general rate expression for the reaction of CO2 with MDEA or any tertiary amine.
Depending on the magnitude of the second term of the denominator of this equation, one can obtain two limiting forms:

The rate expression in this case reduces to:

(3.60)
This form is essentially the expression, which would have been obtained if the second mechanism were used.
Many investigators including Haimor et al. (1987), Critchfield (1988), Tomcej et al. (1989), Little et al. (1990),
Rangwala et al. (1992), and Ko and Li (2000) adopted this form to fit the rate data of the CO2-MDEA system.
The rate constant of the reaction is given as a function of temperature by:

(3.61)
Comparison among the published values of the rate constant at 298.15 K shows a variation between 2.5 and 8.8
lit/mol/sec.

In this case the rate expression is given by:

(3.62)
Glasscock (1990) showed that this form reconciled the published rate data better.
He used activities instead of concentrations to obtain the rate constants. In the current study, the rate expression
represented by the first form (equation 3.60) with the rate constant reported by Critchfield (1988) will be used to model
the kinetics of the CO2 reaction with MDEA. The rate constant reported by Critchfield (1988) is given by:

(3.63)
2.3 CO2 Reaction with Blends of MEA-MDEA and DEA-MDEA
The absorption of CO2 in aqueous solution of blends of MEA-MDEA and DEA-MDEA was studied by Glasscock et
al. (1990), Versteeg et al. (1990), Rangwala et al. (1992), and Hagewiesche et al. (1995). Critchfield showed that the
interaction between MDEA and MEA is insignificant. Therefore the rate expressions (equation 3.37) for MEA and
(equation 3.60) for MDEA are still applicable for the mixture MEA-MDEA. However, for systems containing DEA and MDEA,
the latter acts as another base that neutralizes the zwitterion formed from the reaction of CO2 with DEA.
Hence, The CO2-DEA rate expression for systems containing DEA and MDEA should be corrected by adding the
contribution of MDEA to the neutralization of the zwitterion:
DEA/MDEA:

(3.64)

A value of 468 m6/kmol2/sec was reported in the thesis of Glasscock (1990) for the rate
constant k'R1R2R3N. In this work, this value will be used for
any temperature to compute the absorption rate of CO2in systems containing blends of DEA and MDEA.
Following the suggestion of Glasscock (1990), the effect of MDEA on the rate of reaction of CO2with MEA
will be ignored.
| MEA: |
|
(3.38) |
In contrast, the first term in the denominator of equation (3.35) is negligible compared to the second term for the
CO2-DEA system:
DEA:

(3.39)
Equation 3.39 was used by Laddha and Danckwerts 1981, Blauwhoff et al. (1984), Versteeg and Van Swaaij (1988),
Critchfield (1988), and Glasscock (1990) to describe the kinetics data for the CO2-DEA system.
Glasscock (1990) assumed that the amine and the water are the only bases that contribute to the neutralization of the
zwitterion. The CO2-DEA rate expression reported by Glasscock 1990 will be utilized in this study.
This expression is given by
DEA:

(3.40)
The rate constants reported by Glasscock (1990) were extracted from the fit of the kinetics data and expressed as
functions of temperature according to

(3.41)

(3.42)
2.2 CO2 Reaction with MDEA
CO2 reacts indirectly with MDEA in the presence of water to form bicarbonate and protonated MDEA.
Three different mechanisms have been proposed for this reaction (Barth et al. 1981). The first mechanism suggests that
MDEA neutralizes the species formed by the CO2-water reactions (reactions 3.8 and 3.9). The second mechanism
assumes that MDEA associates with water before reacting with CO2:

(3.43)
The third mechanism follows the zwitterion mechanism described earlier for MEA and DEA:

(3.44)
The zwitterion formed immediately reacts with water and hydroxide to produce respectively bicarbonate and protonated
MDEA and bicarbonate and MDEA according to:
The third mechanism follows the zwitterion mechanism described earlier for MEA and DEA:

(3.45)

(3.46)
Adopting the third mechanism and following the procedure developed earlier for MEA and DEA, the following expression is
obtained for the rate of reaction of CO2 with MDEA:

(3.47)
Combining reactions 3.44 with 3.45 and 3.44 with 3.46 gives:

(3.48)

(3.49)
Reaction 3.48 can also be obtained from combinations of the following reactions:

(3.50)

(3.51)
Hence

(3.52)
Since reaction 3.50 is instantaneous, its products and reactants are at local equilibrium:

(3.53)
Therefore:

(3.54)
Reaction 3.49 can be obtained by combining the instantaneous water dissociation reaction (equation 2.1) with reaction
3.51 to obtain:

(3.55)
or:

(3.56)
Substituting equations 3.54 and 3.56 into equation 3.47 and rearranging gives:

(3.57)
or:

(3.58)
Similar to the derivation of MEA and DEA, the second term in the numerator of equation 3.58 represents the
concentration of CO2 which is in equilibrium with the bicarbonate and the hydroxide ions:

(3.59)
Equation 3.58 is a general rate expression for the reaction of CO2 with MDEA or any tertiary amine.
Depending on the magnitude of the second term of the denominator of this equation, one can obtain two limiting forms:

The rate expression in this case reduces to:

(3.60)
This form is essentially the expression, which would have been obtained if the second mechanism were used.
Many investigators including Haimor et al. (1987), Critchfield (1988), Tomcej et al. (1989), Little et al. (1990),
Rangwala et al. (1992), and Ko and Li (2000) adopted this form to fit the rate data of the CO2-MDEA system.
The rate constant of the reaction is given as a function of temperature by:

(3.61)
Comparison among the published values of the rate constant at 298.15 K shows a variation between 2.5 and 8.8
lit/mol/sec.

In this case the rate expression is given by:

(3.62)
Glasscock (1990) showed that this form reconciled the published rate data better.
He used activities instead of concentrations to obtain the rate constants. In the current study, the rate expression
represented by the first form (equation 3.60) with the rate constant reported by Critchfield (1988) will be used to model
the kinetics of the CO2 reaction with MDEA. The rate constant reported by Critchfield (1988) is given by:

(3.63)
2.3 CO2 Reaction with Blends of MEA-MDEA and DEA-MDEA
The absorption of CO2 in aqueous solution of blends of MEA-MDEA and DEA-MDEA was studied by Glasscock et
al. (1990), Versteeg et al. (1990), Rangwala et al. (1992), and Hagewiesche et al. (1995). Critchfield showed that the
interaction between MDEA and MEA is insignificant. Therefore the rate expressions (equation 3.37) for MEA and
(equation 3.60) for MDEA are still applicable for the mixture MEA-MDEA. However, for systems containing DEA and MDEA,
the latter acts as another base that neutralizes the zwitterion formed from the reaction of CO2 with DEA.
Hence, The CO2-DEA rate expression for systems containing DEA and MDEA should be corrected by adding the
contribution of MDEA to the neutralization of the zwitterion:
DEA/MDEA:

(3.64)

A value of 468 m6/kmol2/sec was reported in the thesis of Glasscock (1990) for the rate
constant k'R1R2R3N. In this work, this value will be used for
any temperature to compute the absorption rate of CO2in systems containing blends of DEA and MDEA.
Following the suggestion of Glasscock (1990), the effect of MDEA on the rate of reaction of CO2with MEA
will be ignored.
| DEA: |
|
(3.39) |
Equation 3.39 was used by Laddha and Danckwerts 1981, Blauwhoff et al. (1984), Versteeg and Van Swaaij (1988),
Critchfield (1988), and Glasscock (1990) to describe the kinetics data for the CO2-DEA system.
Glasscock (1990) assumed that the amine and the water are the only bases that contribute to the neutralization of the
zwitterion. The CO2-DEA rate expression reported by Glasscock 1990 will be utilized in this study.
This expression is given by
DEA:

(3.40)
The rate constants reported by Glasscock (1990) were extracted from the fit of the kinetics data and expressed as
functions of temperature according to

(3.41)

(3.42)
2.2 CO2 Reaction with MDEA
CO2 reacts indirectly with MDEA in the presence of water to form bicarbonate and protonated MDEA.
Three different mechanisms have been proposed for this reaction (Barth et al. 1981). The first mechanism suggests that
MDEA neutralizes the species formed by the CO2-water reactions (reactions 3.8 and 3.9). The second mechanism
assumes that MDEA associates with water before reacting with CO2:

(3.43)
The third mechanism follows the zwitterion mechanism described earlier for MEA and DEA:

(3.44)
The zwitterion formed immediately reacts with water and hydroxide to produce respectively bicarbonate and protonated
MDEA and bicarbonate and MDEA according to:
The third mechanism follows the zwitterion mechanism described earlier for MEA and DEA:

(3.45)

(3.46)
Adopting the third mechanism and following the procedure developed earlier for MEA and DEA, the following expression is
obtained for the rate of reaction of CO2 with MDEA:

(3.47)
Combining reactions 3.44 with 3.45 and 3.44 with 3.46 gives:

(3.48)

(3.49)
Reaction 3.48 can also be obtained from combinations of the following reactions:

(3.50)

(3.51)
Hence

(3.52)
Since reaction 3.50 is instantaneous, its products and reactants are at local equilibrium:

(3.53)
Therefore:

(3.54)
Reaction 3.49 can be obtained by combining the instantaneous water dissociation reaction (equation 2.1) with reaction
3.51 to obtain:

(3.55)
or:

(3.56)
Substituting equations 3.54 and 3.56 into equation 3.47 and rearranging gives:

(3.57)
or:

(3.58)
Similar to the derivation of MEA and DEA, the second term in the numerator of equation 3.58 represents the
concentration of CO2 which is in equilibrium with the bicarbonate and the hydroxide ions:

(3.59)
Equation 3.58 is a general rate expression for the reaction of CO2 with MDEA or any tertiary amine.
Depending on the magnitude of the second term of the denominator of this equation, one can obtain two limiting forms:

The rate expression in this case reduces to:

(3.60)
This form is essentially the expression, which would have been obtained if the second mechanism were used.
Many investigators including Haimor et al. (1987), Critchfield (1988), Tomcej et al. (1989), Little et al. (1990),
Rangwala et al. (1992), and Ko and Li (2000) adopted this form to fit the rate data of the CO2-MDEA system.
The rate constant of the reaction is given as a function of temperature by:

(3.61)
Comparison among the published values of the rate constant at 298.15 K shows a variation between 2.5 and 8.8
lit/mol/sec.

In this case the rate expression is given by:

(3.62)
Glasscock (1990) showed that this form reconciled the published rate data better.
He used activities instead of concentrations to obtain the rate constants. In the current study, the rate expression
represented by the first form (equation 3.60) with the rate constant reported by Critchfield (1988) will be used to model
the kinetics of the CO2 reaction with MDEA. The rate constant reported by Critchfield (1988) is given by:

(3.63)
2.3 CO2 Reaction with Blends of MEA-MDEA and DEA-MDEA
The absorption of CO2 in aqueous solution of blends of MEA-MDEA and DEA-MDEA was studied by Glasscock et
al. (1990), Versteeg et al. (1990), Rangwala et al. (1992), and Hagewiesche et al. (1995). Critchfield showed that the
interaction between MDEA and MEA is insignificant. Therefore the rate expressions (equation 3.37) for MEA and
(equation 3.60) for MDEA are still applicable for the mixture MEA-MDEA. However, for systems containing DEA and MDEA,
the latter acts as another base that neutralizes the zwitterion formed from the reaction of CO2 with DEA.
Hence, The CO2-DEA rate expression for systems containing DEA and MDEA should be corrected by adding the
contribution of MDEA to the neutralization of the zwitterion:
DEA/MDEA:

(3.64)

A value of 468 m6/kmol2/sec was reported in the thesis of Glasscock (1990) for the rate
constant k'R1R2R3N. In this work, this value will be used for
any temperature to compute the absorption rate of CO2in systems containing blends of DEA and MDEA.
Following the suggestion of Glasscock (1990), the effect of MDEA on the rate of reaction of CO2with MEA
will be ignored.
| DEA: |
|
(3.40) |
The rate constants reported by Glasscock (1990) were extracted from the fit of the kinetics data and expressed as
functions of temperature according to

(3.41)

(3.42)
2.2 CO2 Reaction with MDEA
CO2 reacts indirectly with MDEA in the presence of water to form bicarbonate and protonated MDEA.
Three different mechanisms have been proposed for this reaction (Barth et al. 1981). The first mechanism suggests that
MDEA neutralizes the species formed by the CO2-water reactions (reactions 3.8 and 3.9). The second mechanism
assumes that MDEA associates with water before reacting with CO2:

(3.43)
The third mechanism follows the zwitterion mechanism described earlier for MEA and DEA:

(3.44)
The zwitterion formed immediately reacts with water and hydroxide to produce respectively bicarbonate and protonated
MDEA and bicarbonate and MDEA according to:
The third mechanism follows the zwitterion mechanism described earlier for MEA and DEA:

(3.45)

(3.46)
Adopting the third mechanism and following the procedure developed earlier for MEA and DEA, the following expression is
obtained for the rate of reaction of CO2 with MDEA:

(3.47)
Combining reactions 3.44 with 3.45 and 3.44 with 3.46 gives:

(3.48)

(3.49)
Reaction 3.48 can also be obtained from combinations of the following reactions:

(3.50)

(3.51)
Hence

(3.52)
Since reaction 3.50 is instantaneous, its products and reactants are at local equilibrium:

(3.53)
Therefore:

(3.54)
Reaction 3.49 can be obtained by combining the instantaneous water dissociation reaction (equation 2.1) with reaction
3.51 to obtain:

(3.55)
or:

(3.56)
Substituting equations 3.54 and 3.56 into equation 3.47 and rearranging gives:

(3.57)
or:

(3.58)
Similar to the derivation of MEA and DEA, the second term in the numerator of equation 3.58 represents the
concentration of CO2 which is in equilibrium with the bicarbonate and the hydroxide ions:

(3.59)
Equation 3.58 is a general rate expression for the reaction of CO2 with MDEA or any tertiary amine.
Depending on the magnitude of the second term of the denominator of this equation, one can obtain two limiting forms:

The rate expression in this case reduces to:

(3.60)
This form is essentially the expression, which would have been obtained if the second mechanism were used.
Many investigators including Haimor et al. (1987), Critchfield (1988), Tomcej et al. (1989), Little et al. (1990),
Rangwala et al. (1992), and Ko and Li (2000) adopted this form to fit the rate data of the CO2-MDEA system.
The rate constant of the reaction is given as a function of temperature by:

(3.61)
Comparison among the published values of the rate constant at 298.15 K shows a variation between 2.5 and 8.8
lit/mol/sec.

In this case the rate expression is given by:

(3.62)
Glasscock (1990) showed that this form reconciled the published rate data better.
He used activities instead of concentrations to obtain the rate constants. In the current study, the rate expression
represented by the first form (equation 3.60) with the rate constant reported by Critchfield (1988) will be used to model
the kinetics of the CO2 reaction with MDEA. The rate constant reported by Critchfield (1988) is given by:

(3.63)
2.3 CO2 Reaction with Blends of MEA-MDEA and DEA-MDEA
The absorption of CO2 in aqueous solution of blends of MEA-MDEA and DEA-MDEA was studied by Glasscock et
al. (1990), Versteeg et al. (1990), Rangwala et al. (1992), and Hagewiesche et al. (1995). Critchfield showed that the
interaction between MDEA and MEA is insignificant. Therefore the rate expressions (equation 3.37) for MEA and
(equation 3.60) for MDEA are still applicable for the mixture MEA-MDEA. However, for systems containing DEA and MDEA,
the latter acts as another base that neutralizes the zwitterion formed from the reaction of CO2 with DEA.
Hence, The CO2-DEA rate expression for systems containing DEA and MDEA should be corrected by adding the
contribution of MDEA to the neutralization of the zwitterion:
DEA/MDEA:

(3.64)

A value of 468 m6/kmol2/sec was reported in the thesis of Glasscock (1990) for the rate
constant k'R1R2R3N. In this work, this value will be used for
any temperature to compute the absorption rate of CO2in systems containing blends of DEA and MDEA.
Following the suggestion of Glasscock (1990), the effect of MDEA on the rate of reaction of CO2with MEA
will be ignored.
|
|
(3.41) |
|
|
(3.42) |
2.2 CO2 Reaction with MDEA
CO2 reacts indirectly with MDEA in the presence of water to form bicarbonate and protonated MDEA.
Three different mechanisms have been proposed for this reaction (Barth et al. 1981). The first mechanism suggests that
MDEA neutralizes the species formed by the CO2-water reactions (reactions 3.8 and 3.9). The second mechanism
assumes that MDEA associates with water before reacting with CO2:

(3.43)
The third mechanism follows the zwitterion mechanism described earlier for MEA and DEA:

(3.44)
The zwitterion formed immediately reacts with water and hydroxide to produce respectively bicarbonate and protonated
MDEA and bicarbonate and MDEA according to:
The third mechanism follows the zwitterion mechanism described earlier for MEA and DEA:

(3.45)

(3.46)
Adopting the third mechanism and following the procedure developed earlier for MEA and DEA, the following expression is
obtained for the rate of reaction of CO2 with MDEA:

(3.47)
Combining reactions 3.44 with 3.45 and 3.44 with 3.46 gives:

(3.48)

(3.49)
Reaction 3.48 can also be obtained from combinations of the following reactions:

(3.50)

(3.51)
Hence

(3.52)
Since reaction 3.50 is instantaneous, its products and reactants are at local equilibrium:

(3.53)
Therefore:

(3.54)
Reaction 3.49 can be obtained by combining the instantaneous water dissociation reaction (equation 2.1) with reaction
3.51 to obtain:

(3.55)
or:

(3.56)
Substituting equations 3.54 and 3.56 into equation 3.47 and rearranging gives:

(3.57)
or:

(3.58)
Similar to the derivation of MEA and DEA, the second term in the numerator of equation 3.58 represents the
concentration of CO2 which is in equilibrium with the bicarbonate and the hydroxide ions:

(3.59)
Equation 3.58 is a general rate expression for the reaction of CO2 with MDEA or any tertiary amine.
Depending on the magnitude of the second term of the denominator of this equation, one can obtain two limiting forms:

The rate expression in this case reduces to:

(3.60)
This form is essentially the expression, which would have been obtained if the second mechanism were used.
Many investigators including Haimor et al. (1987), Critchfield (1988), Tomcej et al. (1989), Little et al. (1990),
Rangwala et al. (1992), and Ko and Li (2000) adopted this form to fit the rate data of the CO2-MDEA system.
The rate constant of the reaction is given as a function of temperature by:

(3.61)
Comparison among the published values of the rate constant at 298.15 K shows a variation between 2.5 and 8.8
lit/mol/sec.

In this case the rate expression is given by:

(3.62)
Glasscock (1990) showed that this form reconciled the published rate data better.
He used activities instead of concentrations to obtain the rate constants. In the current study, the rate expression
represented by the first form (equation 3.60) with the rate constant reported by Critchfield (1988) will be used to model
the kinetics of the CO2 reaction with MDEA. The rate constant reported by Critchfield (1988) is given by:

(3.63)
2.3 CO2 Reaction with Blends of MEA-MDEA and DEA-MDEA
The absorption of CO2 in aqueous solution of blends of MEA-MDEA and DEA-MDEA was studied by Glasscock et
al. (1990), Versteeg et al. (1990), Rangwala et al. (1992), and Hagewiesche et al. (1995). Critchfield showed that the
interaction between MDEA and MEA is insignificant. Therefore the rate expressions (equation 3.37) for MEA and
(equation 3.60) for MDEA are still applicable for the mixture MEA-MDEA. However, for systems containing DEA and MDEA,
the latter acts as another base that neutralizes the zwitterion formed from the reaction of CO2 with DEA.
Hence, The CO2-DEA rate expression for systems containing DEA and MDEA should be corrected by adding the
contribution of MDEA to the neutralization of the zwitterion:
DEA/MDEA:

(3.64)

A value of 468 m6/kmol2/sec was reported in the thesis of Glasscock (1990) for the rate
constant k'R1R2R3N. In this work, this value will be used for
any temperature to compute the absorption rate of CO2in systems containing blends of DEA and MDEA.
Following the suggestion of Glasscock (1990), the effect of MDEA on the rate of reaction of CO2with MEA
will be ignored.
|
|
(3.43) |
The third mechanism follows the zwitterion mechanism described earlier for MEA and DEA:

(3.44)
The zwitterion formed immediately reacts with water and hydroxide to produce respectively bicarbonate and protonated
MDEA and bicarbonate and MDEA according to:
The third mechanism follows the zwitterion mechanism described earlier for MEA and DEA:

(3.45)

(3.46)
Adopting the third mechanism and following the procedure developed earlier for MEA and DEA, the following expression is
obtained for the rate of reaction of CO2 with MDEA:

(3.47)
Combining reactions 3.44 with 3.45 and 3.44 with 3.46 gives:

(3.48)

(3.49)
Reaction 3.48 can also be obtained from combinations of the following reactions:

(3.50)

(3.51)
Hence

(3.52)
Since reaction 3.50 is instantaneous, its products and reactants are at local equilibrium:

(3.53)
Therefore:

(3.54)
Reaction 3.49 can be obtained by combining the instantaneous water dissociation reaction (equation 2.1) with reaction
3.51 to obtain:

(3.55)
or:

(3.56)
Substituting equations 3.54 and 3.56 into equation 3.47 and rearranging gives:

(3.57)
or:

(3.58)
Similar to the derivation of MEA and DEA, the second term in the numerator of equation 3.58 represents the
concentration of CO2 which is in equilibrium with the bicarbonate and the hydroxide ions:

(3.59)
Equation 3.58 is a general rate expression for the reaction of CO2 with MDEA or any tertiary amine.
Depending on the magnitude of the second term of the denominator of this equation, one can obtain two limiting forms:

The rate expression in this case reduces to:

(3.60)
This form is essentially the expression, which would have been obtained if the second mechanism were used.
Many investigators including Haimor et al. (1987), Critchfield (1988), Tomcej et al. (1989), Little et al. (1990),
Rangwala et al. (1992), and Ko and Li (2000) adopted this form to fit the rate data of the CO2-MDEA system.
The rate constant of the reaction is given as a function of temperature by:

(3.61)
Comparison among the published values of the rate constant at 298.15 K shows a variation between 2.5 and 8.8
lit/mol/sec.

In this case the rate expression is given by:

(3.62)
Glasscock (1990) showed that this form reconciled the published rate data better.
He used activities instead of concentrations to obtain the rate constants. In the current study, the rate expression
represented by the first form (equation 3.60) with the rate constant reported by Critchfield (1988) will be used to model
the kinetics of the CO2 reaction with MDEA. The rate constant reported by Critchfield (1988) is given by:

(3.63)
2.3 CO2 Reaction with Blends of MEA-MDEA and DEA-MDEA
The absorption of CO2 in aqueous solution of blends of MEA-MDEA and DEA-MDEA was studied by Glasscock et
al. (1990), Versteeg et al. (1990), Rangwala et al. (1992), and Hagewiesche et al. (1995). Critchfield showed that the
interaction between MDEA and MEA is insignificant. Therefore the rate expressions (equation 3.37) for MEA and
(equation 3.60) for MDEA are still applicable for the mixture MEA-MDEA. However, for systems containing DEA and MDEA,
the latter acts as another base that neutralizes the zwitterion formed from the reaction of CO2 with DEA.
Hence, The CO2-DEA rate expression for systems containing DEA and MDEA should be corrected by adding the
contribution of MDEA to the neutralization of the zwitterion:
DEA/MDEA:

(3.64)

A value of 468 m6/kmol2/sec was reported in the thesis of Glasscock (1990) for the rate
constant k'R1R2R3N. In this work, this value will be used for
any temperature to compute the absorption rate of CO2in systems containing blends of DEA and MDEA.
Following the suggestion of Glasscock (1990), the effect of MDEA on the rate of reaction of CO2with MEA
will be ignored.
|
|
(3.44) |
The zwitterion formed immediately reacts with water and hydroxide to produce respectively bicarbonate and protonated
MDEA and bicarbonate and MDEA according to:
The third mechanism follows the zwitterion mechanism described earlier for MEA and DEA:

(3.45)

(3.46)
Adopting the third mechanism and following the procedure developed earlier for MEA and DEA, the following expression is
obtained for the rate of reaction of CO2 with MDEA:

(3.47)
Combining reactions 3.44 with 3.45 and 3.44 with 3.46 gives:

(3.48)

(3.49)
Reaction 3.48 can also be obtained from combinations of the following reactions:

(3.50)

(3.51)
Hence

(3.52)
Since reaction 3.50 is instantaneous, its products and reactants are at local equilibrium:

(3.53)
Therefore:

(3.54)
Reaction 3.49 can be obtained by combining the instantaneous water dissociation reaction (equation 2.1) with reaction
3.51 to obtain:

(3.55)
or:

(3.56)
Substituting equations 3.54 and 3.56 into equation 3.47 and rearranging gives:

(3.57)
or:

(3.58)
Similar to the derivation of MEA and DEA, the second term in the numerator of equation 3.58 represents the
concentration of CO2 which is in equilibrium with the bicarbonate and the hydroxide ions:

(3.59)
Equation 3.58 is a general rate expression for the reaction of CO2 with MDEA or any tertiary amine.
Depending on the magnitude of the second term of the denominator of this equation, one can obtain two limiting forms:

The rate expression in this case reduces to:

(3.60)
This form is essentially the expression, which would have been obtained if the second mechanism were used.
Many investigators including Haimor et al. (1987), Critchfield (1988), Tomcej et al. (1989), Little et al. (1990),
Rangwala et al. (1992), and Ko and Li (2000) adopted this form to fit the rate data of the CO2-MDEA system.
The rate constant of the reaction is given as a function of temperature by:

(3.61)
Comparison among the published values of the rate constant at 298.15 K shows a variation between 2.5 and 8.8
lit/mol/sec.

In this case the rate expression is given by:

(3.62)
Glasscock (1990) showed that this form reconciled the published rate data better.
He used activities instead of concentrations to obtain the rate constants. In the current study, the rate expression
represented by the first form (equation 3.60) with the rate constant reported by Critchfield (1988) will be used to model
the kinetics of the CO2 reaction with MDEA. The rate constant reported by Critchfield (1988) is given by:

(3.63)
2.3 CO2 Reaction with Blends of MEA-MDEA and DEA-MDEA
The absorption of CO2 in aqueous solution of blends of MEA-MDEA and DEA-MDEA was studied by Glasscock et
al. (1990), Versteeg et al. (1990), Rangwala et al. (1992), and Hagewiesche et al. (1995). Critchfield showed that the
interaction between MDEA and MEA is insignificant. Therefore the rate expressions (equation 3.37) for MEA and
(equation 3.60) for MDEA are still applicable for the mixture MEA-MDEA. However, for systems containing DEA and MDEA,
the latter acts as another base that neutralizes the zwitterion formed from the reaction of CO2 with DEA.
Hence, The CO2-DEA rate expression for systems containing DEA and MDEA should be corrected by adding the
contribution of MDEA to the neutralization of the zwitterion:
DEA/MDEA:

(3.64)

A value of 468 m6/kmol2/sec was reported in the thesis of Glasscock (1990) for the rate
constant k'R1R2R3N. In this work, this value will be used for
any temperature to compute the absorption rate of CO2in systems containing blends of DEA and MDEA.
Following the suggestion of Glasscock (1990), the effect of MDEA on the rate of reaction of CO2with MEA
will be ignored.
The third mechanism follows the zwitterion mechanism described earlier for MEA and DEA:

(3.45)

(3.46)
Adopting the third mechanism and following the procedure developed earlier for MEA and DEA, the following expression is
obtained for the rate of reaction of CO2 with MDEA:

(3.47)
Combining reactions 3.44 with 3.45 and 3.44 with 3.46 gives:

(3.48)

(3.49)
Reaction 3.48 can also be obtained from combinations of the following reactions:

(3.50)

(3.51)
Hence

(3.52)
Since reaction 3.50 is instantaneous, its products and reactants are at local equilibrium:

(3.53)
Therefore:

(3.54)
Reaction 3.49 can be obtained by combining the instantaneous water dissociation reaction (equation 2.1) with reaction
3.51 to obtain:

(3.55)
or:

(3.56)
Substituting equations 3.54 and 3.56 into equation 3.47 and rearranging gives:

(3.57)
or:

(3.58)
Similar to the derivation of MEA and DEA, the second term in the numerator of equation 3.58 represents the
concentration of CO2 which is in equilibrium with the bicarbonate and the hydroxide ions:

(3.59)
Equation 3.58 is a general rate expression for the reaction of CO2 with MDEA or any tertiary amine.
Depending on the magnitude of the second term of the denominator of this equation, one can obtain two limiting forms:

The rate expression in this case reduces to:

(3.60)
This form is essentially the expression, which would have been obtained if the second mechanism were used.
Many investigators including Haimor et al. (1987), Critchfield (1988), Tomcej et al. (1989), Little et al. (1990),
Rangwala et al. (1992), and Ko and Li (2000) adopted this form to fit the rate data of the CO2-MDEA system.
The rate constant of the reaction is given as a function of temperature by:

(3.61)
Comparison among the published values of the rate constant at 298.15 K shows a variation between 2.5 and 8.8
lit/mol/sec.

In this case the rate expression is given by:

(3.62)
Glasscock (1990) showed that this form reconciled the published rate data better.
He used activities instead of concentrations to obtain the rate constants. In the current study, the rate expression
represented by the first form (equation 3.60) with the rate constant reported by Critchfield (1988) will be used to model
the kinetics of the CO2 reaction with MDEA. The rate constant reported by Critchfield (1988) is given by:

(3.63)
2.3 CO2 Reaction with Blends of MEA-MDEA and DEA-MDEA
The absorption of CO2 in aqueous solution of blends of MEA-MDEA and DEA-MDEA was studied by Glasscock et
al. (1990), Versteeg et al. (1990), Rangwala et al. (1992), and Hagewiesche et al. (1995). Critchfield showed that the
interaction between MDEA and MEA is insignificant. Therefore the rate expressions (equation 3.37) for MEA and
(equation 3.60) for MDEA are still applicable for the mixture MEA-MDEA. However, for systems containing DEA and MDEA,
the latter acts as another base that neutralizes the zwitterion formed from the reaction of CO2 with DEA.
Hence, The CO2-DEA rate expression for systems containing DEA and MDEA should be corrected by adding the
contribution of MDEA to the neutralization of the zwitterion:
DEA/MDEA:

(3.64)

A value of 468 m6/kmol2/sec was reported in the thesis of Glasscock (1990) for the rate
constant k'R1R2R3N. In this work, this value will be used for
any temperature to compute the absorption rate of CO2in systems containing blends of DEA and MDEA.
Following the suggestion of Glasscock (1990), the effect of MDEA on the rate of reaction of CO2with MEA
will be ignored.
|
|
(3.45) |
|
|
(3.46) |
Adopting the third mechanism and following the procedure developed earlier for MEA and DEA, the following expression is
obtained for the rate of reaction of CO2 with MDEA:

(3.47)
Combining reactions 3.44 with 3.45 and 3.44 with 3.46 gives:

(3.48)

(3.49)
Reaction 3.48 can also be obtained from combinations of the following reactions:

(3.50)

(3.51)
Hence

(3.52)
Since reaction 3.50 is instantaneous, its products and reactants are at local equilibrium:

(3.53)
Therefore:

(3.54)
Reaction 3.49 can be obtained by combining the instantaneous water dissociation reaction (equation 2.1) with reaction
3.51 to obtain:

(3.55)
or:

(3.56)
Substituting equations 3.54 and 3.56 into equation 3.47 and rearranging gives:

(3.57)
or:

(3.58)
Similar to the derivation of MEA and DEA, the second term in the numerator of equation 3.58 represents the
concentration of CO2 which is in equilibrium with the bicarbonate and the hydroxide ions:

(3.59)
Equation 3.58 is a general rate expression for the reaction of CO2 with MDEA or any tertiary amine.
Depending on the magnitude of the second term of the denominator of this equation, one can obtain two limiting forms:

The rate expression in this case reduces to:

(3.60)
This form is essentially the expression, which would have been obtained if the second mechanism were used.
Many investigators including Haimor et al. (1987), Critchfield (1988), Tomcej et al. (1989), Little et al. (1990),
Rangwala et al. (1992), and Ko and Li (2000) adopted this form to fit the rate data of the CO2-MDEA system.
The rate constant of the reaction is given as a function of temperature by:

(3.61)
Comparison among the published values of the rate constant at 298.15 K shows a variation between 2.5 and 8.8
lit/mol/sec.

In this case the rate expression is given by:

(3.62)
Glasscock (1990) showed that this form reconciled the published rate data better.
He used activities instead of concentrations to obtain the rate constants. In the current study, the rate expression
represented by the first form (equation 3.60) with the rate constant reported by Critchfield (1988) will be used to model
the kinetics of the CO2 reaction with MDEA. The rate constant reported by Critchfield (1988) is given by:

(3.63)
2.3 CO2 Reaction with Blends of MEA-MDEA and DEA-MDEA
The absorption of CO2 in aqueous solution of blends of MEA-MDEA and DEA-MDEA was studied by Glasscock et
al. (1990), Versteeg et al. (1990), Rangwala et al. (1992), and Hagewiesche et al. (1995). Critchfield showed that the
interaction between MDEA and MEA is insignificant. Therefore the rate expressions (equation 3.37) for MEA and
(equation 3.60) for MDEA are still applicable for the mixture MEA-MDEA. However, for systems containing DEA and MDEA,
the latter acts as another base that neutralizes the zwitterion formed from the reaction of CO2 with DEA.
Hence, The CO2-DEA rate expression for systems containing DEA and MDEA should be corrected by adding the
contribution of MDEA to the neutralization of the zwitterion:
DEA/MDEA:

(3.64)

A value of 468 m6/kmol2/sec was reported in the thesis of Glasscock (1990) for the rate
constant k'R1R2R3N. In this work, this value will be used for
any temperature to compute the absorption rate of CO2in systems containing blends of DEA and MDEA.
Following the suggestion of Glasscock (1990), the effect of MDEA on the rate of reaction of CO2with MEA
will be ignored.
|
|
(3.47) |
Combining reactions 3.44 with 3.45 and 3.44 with 3.46 gives:

(3.48)

(3.49)
Reaction 3.48 can also be obtained from combinations of the following reactions:

(3.50)

(3.51)
Hence

(3.52)
Since reaction 3.50 is instantaneous, its products and reactants are at local equilibrium:

(3.53)
Therefore:

(3.54)
Reaction 3.49 can be obtained by combining the instantaneous water dissociation reaction (equation 2.1) with reaction
3.51 to obtain:

(3.55)
or:

(3.56)
Substituting equations 3.54 and 3.56 into equation 3.47 and rearranging gives:

(3.57)
or:

(3.58)
Similar to the derivation of MEA and DEA, the second term in the numerator of equation 3.58 represents the
concentration of CO2 which is in equilibrium with the bicarbonate and the hydroxide ions:

(3.59)
Equation 3.58 is a general rate expression for the reaction of CO2 with MDEA or any tertiary amine.
Depending on the magnitude of the second term of the denominator of this equation, one can obtain two limiting forms:

The rate expression in this case reduces to:

(3.60)
This form is essentially the expression, which would have been obtained if the second mechanism were used.
Many investigators including Haimor et al. (1987), Critchfield (1988), Tomcej et al. (1989), Little et al. (1990),
Rangwala et al. (1992), and Ko and Li (2000) adopted this form to fit the rate data of the CO2-MDEA system.
The rate constant of the reaction is given as a function of temperature by:

(3.61)
Comparison among the published values of the rate constant at 298.15 K shows a variation between 2.5 and 8.8
lit/mol/sec.

In this case the rate expression is given by:

(3.62)
Glasscock (1990) showed that this form reconciled the published rate data better.
He used activities instead of concentrations to obtain the rate constants. In the current study, the rate expression
represented by the first form (equation 3.60) with the rate constant reported by Critchfield (1988) will be used to model
the kinetics of the CO2 reaction with MDEA. The rate constant reported by Critchfield (1988) is given by:

(3.63)
2.3 CO2 Reaction with Blends of MEA-MDEA and DEA-MDEA
The absorption of CO2 in aqueous solution of blends of MEA-MDEA and DEA-MDEA was studied by Glasscock et
al. (1990), Versteeg et al. (1990), Rangwala et al. (1992), and Hagewiesche et al. (1995). Critchfield showed that the
interaction between MDEA and MEA is insignificant. Therefore the rate expressions (equation 3.37) for MEA and
(equation 3.60) for MDEA are still applicable for the mixture MEA-MDEA. However, for systems containing DEA and MDEA,
the latter acts as another base that neutralizes the zwitterion formed from the reaction of CO2 with DEA.
Hence, The CO2-DEA rate expression for systems containing DEA and MDEA should be corrected by adding the
contribution of MDEA to the neutralization of the zwitterion:
DEA/MDEA:

(3.64)

A value of 468 m6/kmol2/sec was reported in the thesis of Glasscock (1990) for the rate
constant k'R1R2R3N. In this work, this value will be used for
any temperature to compute the absorption rate of CO2in systems containing blends of DEA and MDEA.
Following the suggestion of Glasscock (1990), the effect of MDEA on the rate of reaction of CO2with MEA
will be ignored.
|
|
(3.48) |
|
|
(3.49) |
Reaction 3.48 can also be obtained from combinations of the following reactions:

(3.50)

(3.51)
Hence

(3.52)
Since reaction 3.50 is instantaneous, its products and reactants are at local equilibrium:

(3.53)
Therefore:

(3.54)
Reaction 3.49 can be obtained by combining the instantaneous water dissociation reaction (equation 2.1) with reaction
3.51 to obtain:

(3.55)
or:

(3.56)
Substituting equations 3.54 and 3.56 into equation 3.47 and rearranging gives:

(3.57)
or:

(3.58)
Similar to the derivation of MEA and DEA, the second term in the numerator of equation 3.58 represents the
concentration of CO2 which is in equilibrium with the bicarbonate and the hydroxide ions:

(3.59)
Equation 3.58 is a general rate expression for the reaction of CO2 with MDEA or any tertiary amine.
Depending on the magnitude of the second term of the denominator of this equation, one can obtain two limiting forms:

The rate expression in this case reduces to:

(3.60)
This form is essentially the expression, which would have been obtained if the second mechanism were used.
Many investigators including Haimor et al. (1987), Critchfield (1988), Tomcej et al. (1989), Little et al. (1990),
Rangwala et al. (1992), and Ko and Li (2000) adopted this form to fit the rate data of the CO2-MDEA system.
The rate constant of the reaction is given as a function of temperature by:

(3.61)
Comparison among the published values of the rate constant at 298.15 K shows a variation between 2.5 and 8.8
lit/mol/sec.

In this case the rate expression is given by:

(3.62)
Glasscock (1990) showed that this form reconciled the published rate data better.
He used activities instead of concentrations to obtain the rate constants. In the current study, the rate expression
represented by the first form (equation 3.60) with the rate constant reported by Critchfield (1988) will be used to model
the kinetics of the CO2 reaction with MDEA. The rate constant reported by Critchfield (1988) is given by:

(3.63)
2.3 CO2 Reaction with Blends of MEA-MDEA and DEA-MDEA
The absorption of CO2 in aqueous solution of blends of MEA-MDEA and DEA-MDEA was studied by Glasscock et
al. (1990), Versteeg et al. (1990), Rangwala et al. (1992), and Hagewiesche et al. (1995). Critchfield showed that the
interaction between MDEA and MEA is insignificant. Therefore the rate expressions (equation 3.37) for MEA and
(equation 3.60) for MDEA are still applicable for the mixture MEA-MDEA. However, for systems containing DEA and MDEA,
the latter acts as another base that neutralizes the zwitterion formed from the reaction of CO2 with DEA.
Hence, The CO2-DEA rate expression for systems containing DEA and MDEA should be corrected by adding the
contribution of MDEA to the neutralization of the zwitterion:
DEA/MDEA:

(3.64)

A value of 468 m6/kmol2/sec was reported in the thesis of Glasscock (1990) for the rate
constant k'R1R2R3N. In this work, this value will be used for
any temperature to compute the absorption rate of CO2in systems containing blends of DEA and MDEA.
Following the suggestion of Glasscock (1990), the effect of MDEA on the rate of reaction of CO2with MEA
will be ignored.
|
|
(3.50) |
|
|
(3.51) |
Hence

(3.52)
Since reaction 3.50 is instantaneous, its products and reactants are at local equilibrium:

(3.53)
Therefore:

(3.54)
Reaction 3.49 can be obtained by combining the instantaneous water dissociation reaction (equation 2.1) with reaction
3.51 to obtain:

(3.55)
or:

(3.56)
Substituting equations 3.54 and 3.56 into equation 3.47 and rearranging gives:

(3.57)
or:

(3.58)
Similar to the derivation of MEA and DEA, the second term in the numerator of equation 3.58 represents the
concentration of CO2 which is in equilibrium with the bicarbonate and the hydroxide ions:

(3.59)
Equation 3.58 is a general rate expression for the reaction of CO2 with MDEA or any tertiary amine.
Depending on the magnitude of the second term of the denominator of this equation, one can obtain two limiting forms:

The rate expression in this case reduces to:

(3.60)
This form is essentially the expression, which would have been obtained if the second mechanism were used.
Many investigators including Haimor et al. (1987), Critchfield (1988), Tomcej et al. (1989), Little et al. (1990),
Rangwala et al. (1992), and Ko and Li (2000) adopted this form to fit the rate data of the CO2-MDEA system.
The rate constant of the reaction is given as a function of temperature by:

(3.61)
Comparison among the published values of the rate constant at 298.15 K shows a variation between 2.5 and 8.8
lit/mol/sec.

In this case the rate expression is given by:

(3.62)
Glasscock (1990) showed that this form reconciled the published rate data better.
He used activities instead of concentrations to obtain the rate constants. In the current study, the rate expression
represented by the first form (equation 3.60) with the rate constant reported by Critchfield (1988) will be used to model
the kinetics of the CO2 reaction with MDEA. The rate constant reported by Critchfield (1988) is given by:

(3.63)
2.3 CO2 Reaction with Blends of MEA-MDEA and DEA-MDEA
The absorption of CO2 in aqueous solution of blends of MEA-MDEA and DEA-MDEA was studied by Glasscock et
al. (1990), Versteeg et al. (1990), Rangwala et al. (1992), and Hagewiesche et al. (1995). Critchfield showed that the
interaction between MDEA and MEA is insignificant. Therefore the rate expressions (equation 3.37) for MEA and
(equation 3.60) for MDEA are still applicable for the mixture MEA-MDEA. However, for systems containing DEA and MDEA,
the latter acts as another base that neutralizes the zwitterion formed from the reaction of CO2 with DEA.
Hence, The CO2-DEA rate expression for systems containing DEA and MDEA should be corrected by adding the
contribution of MDEA to the neutralization of the zwitterion:
DEA/MDEA:

(3.64)

A value of 468 m6/kmol2/sec was reported in the thesis of Glasscock (1990) for the rate
constant k'R1R2R3N. In this work, this value will be used for
any temperature to compute the absorption rate of CO2in systems containing blends of DEA and MDEA.
Following the suggestion of Glasscock (1990), the effect of MDEA on the rate of reaction of CO2with MEA
will be ignored.
|
|
(3.52) |
Since reaction 3.50 is instantaneous, its products and reactants are at local equilibrium:

(3.53)
Therefore:

(3.54)
Reaction 3.49 can be obtained by combining the instantaneous water dissociation reaction (equation 2.1) with reaction
3.51 to obtain:

(3.55)
or:

(3.56)
Substituting equations 3.54 and 3.56 into equation 3.47 and rearranging gives:

(3.57)
or:

(3.58)
Similar to the derivation of MEA and DEA, the second term in the numerator of equation 3.58 represents the
concentration of CO2 which is in equilibrium with the bicarbonate and the hydroxide ions:

(3.59)
Equation 3.58 is a general rate expression for the reaction of CO2 with MDEA or any tertiary amine.
Depending on the magnitude of the second term of the denominator of this equation, one can obtain two limiting forms:

The rate expression in this case reduces to:

(3.60)
This form is essentially the expression, which would have been obtained if the second mechanism were used.
Many investigators including Haimor et al. (1987), Critchfield (1988), Tomcej et al. (1989), Little et al. (1990),
Rangwala et al. (1992), and Ko and Li (2000) adopted this form to fit the rate data of the CO2-MDEA system.
The rate constant of the reaction is given as a function of temperature by:

(3.61)
Comparison among the published values of the rate constant at 298.15 K shows a variation between 2.5 and 8.8
lit/mol/sec.

In this case the rate expression is given by:

(3.62)
Glasscock (1990) showed that this form reconciled the published rate data better.
He used activities instead of concentrations to obtain the rate constants. In the current study, the rate expression
represented by the first form (equation 3.60) with the rate constant reported by Critchfield (1988) will be used to model
the kinetics of the CO2 reaction with MDEA. The rate constant reported by Critchfield (1988) is given by:

(3.63)
2.3 CO2 Reaction with Blends of MEA-MDEA and DEA-MDEA
The absorption of CO2 in aqueous solution of blends of MEA-MDEA and DEA-MDEA was studied by Glasscock et
al. (1990), Versteeg et al. (1990), Rangwala et al. (1992), and Hagewiesche et al. (1995). Critchfield showed that the
interaction between MDEA and MEA is insignificant. Therefore the rate expressions (equation 3.37) for MEA and
(equation 3.60) for MDEA are still applicable for the mixture MEA-MDEA. However, for systems containing DEA and MDEA,
the latter acts as another base that neutralizes the zwitterion formed from the reaction of CO2 with DEA.
Hence, The CO2-DEA rate expression for systems containing DEA and MDEA should be corrected by adding the
contribution of MDEA to the neutralization of the zwitterion:
DEA/MDEA:

(3.64)

A value of 468 m6/kmol2/sec was reported in the thesis of Glasscock (1990) for the rate
constant k'R1R2R3N. In this work, this value will be used for
any temperature to compute the absorption rate of CO2in systems containing blends of DEA and MDEA.
Following the suggestion of Glasscock (1990), the effect of MDEA on the rate of reaction of CO2with MEA
will be ignored.
|
|
(3.53) |
Therefore:

(3.54)
Reaction 3.49 can be obtained by combining the instantaneous water dissociation reaction (equation 2.1) with reaction
3.51 to obtain:

(3.55)
or:

(3.56)
Substituting equations 3.54 and 3.56 into equation 3.47 and rearranging gives:

(3.57)
or:

(3.58)
Similar to the derivation of MEA and DEA, the second term in the numerator of equation 3.58 represents the
concentration of CO2 which is in equilibrium with the bicarbonate and the hydroxide ions:

(3.59)
Equation 3.58 is a general rate expression for the reaction of CO2 with MDEA or any tertiary amine.
Depending on the magnitude of the second term of the denominator of this equation, one can obtain two limiting forms:

The rate expression in this case reduces to:

(3.60)
This form is essentially the expression, which would have been obtained if the second mechanism were used.
Many investigators including Haimor et al. (1987), Critchfield (1988), Tomcej et al. (1989), Little et al. (1990),
Rangwala et al. (1992), and Ko and Li (2000) adopted this form to fit the rate data of the CO2-MDEA system.
The rate constant of the reaction is given as a function of temperature by:

(3.61)
Comparison among the published values of the rate constant at 298.15 K shows a variation between 2.5 and 8.8
lit/mol/sec.

In this case the rate expression is given by:

(3.62)
Glasscock (1990) showed that this form reconciled the published rate data better.
He used activities instead of concentrations to obtain the rate constants. In the current study, the rate expression
represented by the first form (equation 3.60) with the rate constant reported by Critchfield (1988) will be used to model
the kinetics of the CO2 reaction with MDEA. The rate constant reported by Critchfield (1988) is given by:

(3.63)
2.3 CO2 Reaction with Blends of MEA-MDEA and DEA-MDEA
The absorption of CO2 in aqueous solution of blends of MEA-MDEA and DEA-MDEA was studied by Glasscock et
al. (1990), Versteeg et al. (1990), Rangwala et al. (1992), and Hagewiesche et al. (1995). Critchfield showed that the
interaction between MDEA and MEA is insignificant. Therefore the rate expressions (equation 3.37) for MEA and
(equation 3.60) for MDEA are still applicable for the mixture MEA-MDEA. However, for systems containing DEA and MDEA,
the latter acts as another base that neutralizes the zwitterion formed from the reaction of CO2 with DEA.
Hence, The CO2-DEA rate expression for systems containing DEA and MDEA should be corrected by adding the
contribution of MDEA to the neutralization of the zwitterion:
DEA/MDEA:

(3.64)

A value of 468 m6/kmol2/sec was reported in the thesis of Glasscock (1990) for the rate
constant k'R1R2R3N. In this work, this value will be used for
any temperature to compute the absorption rate of CO2in systems containing blends of DEA and MDEA.
Following the suggestion of Glasscock (1990), the effect of MDEA on the rate of reaction of CO2with MEA
will be ignored.
|
|
(3.54) |
Reaction 3.49 can be obtained by combining the instantaneous water dissociation reaction (equation 2.1) with reaction
3.51 to obtain:

(3.55)
or:

(3.56)
Substituting equations 3.54 and 3.56 into equation 3.47 and rearranging gives:

(3.57)
or:

(3.58)
Similar to the derivation of MEA and DEA, the second term in the numerator of equation 3.58 represents the
concentration of CO2 which is in equilibrium with the bicarbonate and the hydroxide ions:

(3.59)
Equation 3.58 is a general rate expression for the reaction of CO2 with MDEA or any tertiary amine.
Depending on the magnitude of the second term of the denominator of this equation, one can obtain two limiting forms:

The rate expression in this case reduces to:

(3.60)
This form is essentially the expression, which would have been obtained if the second mechanism were used.
Many investigators including Haimor et al. (1987), Critchfield (1988), Tomcej et al. (1989), Little et al. (1990),
Rangwala et al. (1992), and Ko and Li (2000) adopted this form to fit the rate data of the CO2-MDEA system.
The rate constant of the reaction is given as a function of temperature by:

(3.61)
Comparison among the published values of the rate constant at 298.15 K shows a variation between 2.5 and 8.8
lit/mol/sec.

In this case the rate expression is given by:

(3.62)
Glasscock (1990) showed that this form reconciled the published rate data better.
He used activities instead of concentrations to obtain the rate constants. In the current study, the rate expression
represented by the first form (equation 3.60) with the rate constant reported by Critchfield (1988) will be used to model
the kinetics of the CO2 reaction with MDEA. The rate constant reported by Critchfield (1988) is given by:

(3.63)
2.3 CO2 Reaction with Blends of MEA-MDEA and DEA-MDEA
The absorption of CO2 in aqueous solution of blends of MEA-MDEA and DEA-MDEA was studied by Glasscock et
al. (1990), Versteeg et al. (1990), Rangwala et al. (1992), and Hagewiesche et al. (1995). Critchfield showed that the
interaction between MDEA and MEA is insignificant. Therefore the rate expressions (equation 3.37) for MEA and
(equation 3.60) for MDEA are still applicable for the mixture MEA-MDEA. However, for systems containing DEA and MDEA,
the latter acts as another base that neutralizes the zwitterion formed from the reaction of CO2 with DEA.
Hence, The CO2-DEA rate expression for systems containing DEA and MDEA should be corrected by adding the
contribution of MDEA to the neutralization of the zwitterion:
DEA/MDEA:

(3.64)

A value of 468 m6/kmol2/sec was reported in the thesis of Glasscock (1990) for the rate
constant k'R1R2R3N. In this work, this value will be used for
any temperature to compute the absorption rate of CO2in systems containing blends of DEA and MDEA.
Following the suggestion of Glasscock (1990), the effect of MDEA on the rate of reaction of CO2with MEA
will be ignored.
|
|
(3.55) |
or:
|
|
(3.56) |
Substituting equations 3.54 and 3.56 into equation 3.47 and rearranging gives:

(3.57)
or:

(3.58)
Similar to the derivation of MEA and DEA, the second term in the numerator of equation 3.58 represents the
concentration of CO2 which is in equilibrium with the bicarbonate and the hydroxide ions:

(3.59)
Equation 3.58 is a general rate expression for the reaction of CO2 with MDEA or any tertiary amine.
Depending on the magnitude of the second term of the denominator of this equation, one can obtain two limiting forms:

The rate expression in this case reduces to:

(3.60)
This form is essentially the expression, which would have been obtained if the second mechanism were used.
Many investigators including Haimor et al. (1987), Critchfield (1988), Tomcej et al. (1989), Little et al. (1990),
Rangwala et al. (1992), and Ko and Li (2000) adopted this form to fit the rate data of the CO2-MDEA system.
The rate constant of the reaction is given as a function of temperature by:

(3.61)
Comparison among the published values of the rate constant at 298.15 K shows a variation between 2.5 and 8.8
lit/mol/sec.

In this case the rate expression is given by:

(3.62)
Glasscock (1990) showed that this form reconciled the published rate data better.
He used activities instead of concentrations to obtain the rate constants. In the current study, the rate expression
represented by the first form (equation 3.60) with the rate constant reported by Critchfield (1988) will be used to model
the kinetics of the CO2 reaction with MDEA. The rate constant reported by Critchfield (1988) is given by:

(3.63)
2.3 CO2 Reaction with Blends of MEA-MDEA and DEA-MDEA
The absorption of CO2 in aqueous solution of blends of MEA-MDEA and DEA-MDEA was studied by Glasscock et
al. (1990), Versteeg et al. (1990), Rangwala et al. (1992), and Hagewiesche et al. (1995). Critchfield showed that the
interaction between MDEA and MEA is insignificant. Therefore the rate expressions (equation 3.37) for MEA and
(equation 3.60) for MDEA are still applicable for the mixture MEA-MDEA. However, for systems containing DEA and MDEA,
the latter acts as another base that neutralizes the zwitterion formed from the reaction of CO2 with DEA.
Hence, The CO2-DEA rate expression for systems containing DEA and MDEA should be corrected by adding the
contribution of MDEA to the neutralization of the zwitterion:
DEA/MDEA:

(3.64)

A value of 468 m6/kmol2/sec was reported in the thesis of Glasscock (1990) for the rate
constant k'R1R2R3N. In this work, this value will be used for
any temperature to compute the absorption rate of CO2in systems containing blends of DEA and MDEA.
Following the suggestion of Glasscock (1990), the effect of MDEA on the rate of reaction of CO2with MEA
will be ignored.
|
|
(3.57) |
or:
|
|
(3.58) |
Similar to the derivation of MEA and DEA, the second term in the numerator of equation 3.58 represents the
concentration of CO2 which is in equilibrium with the bicarbonate and the hydroxide ions:

(3.59)
Equation 3.58 is a general rate expression for the reaction of CO2 with MDEA or any tertiary amine.
Depending on the magnitude of the second term of the denominator of this equation, one can obtain two limiting forms:

The rate expression in this case reduces to:

(3.60)
This form is essentially the expression, which would have been obtained if the second mechanism were used.
Many investigators including Haimor et al. (1987), Critchfield (1988), Tomcej et al. (1989), Little et al. (1990),
Rangwala et al. (1992), and Ko and Li (2000) adopted this form to fit the rate data of the CO2-MDEA system.
The rate constant of the reaction is given as a function of temperature by:

(3.61)
Comparison among the published values of the rate constant at 298.15 K shows a variation between 2.5 and 8.8
lit/mol/sec.

In this case the rate expression is given by:

(3.62)
Glasscock (1990) showed that this form reconciled the published rate data better.
He used activities instead of concentrations to obtain the rate constants. In the current study, the rate expression
represented by the first form (equation 3.60) with the rate constant reported by Critchfield (1988) will be used to model
the kinetics of the CO2 reaction with MDEA. The rate constant reported by Critchfield (1988) is given by:

(3.63)
2.3 CO2 Reaction with Blends of MEA-MDEA and DEA-MDEA
The absorption of CO2 in aqueous solution of blends of MEA-MDEA and DEA-MDEA was studied by Glasscock et
al. (1990), Versteeg et al. (1990), Rangwala et al. (1992), and Hagewiesche et al. (1995). Critchfield showed that the
interaction between MDEA and MEA is insignificant. Therefore the rate expressions (equation 3.37) for MEA and
(equation 3.60) for MDEA are still applicable for the mixture MEA-MDEA. However, for systems containing DEA and MDEA,
the latter acts as another base that neutralizes the zwitterion formed from the reaction of CO2 with DEA.
Hence, The CO2-DEA rate expression for systems containing DEA and MDEA should be corrected by adding the
contribution of MDEA to the neutralization of the zwitterion:
DEA/MDEA:

(3.64)

A value of 468 m6/kmol2/sec was reported in the thesis of Glasscock (1990) for the rate
constant k'R1R2R3N. In this work, this value will be used for
any temperature to compute the absorption rate of CO2in systems containing blends of DEA and MDEA.
Following the suggestion of Glasscock (1990), the effect of MDEA on the rate of reaction of CO2with MEA
will be ignored.
|
|
(3.59) |
Equation 3.58 is a general rate expression for the reaction of CO2 with MDEA or any tertiary amine.
Depending on the magnitude of the second term of the denominator of this equation, one can obtain two limiting forms:

The rate expression in this case reduces to:

(3.60)
This form is essentially the expression, which would have been obtained if the second mechanism were used.
Many investigators including Haimor et al. (1987), Critchfield (1988), Tomcej et al. (1989), Little et al. (1990),
Rangwala et al. (1992), and Ko and Li (2000) adopted this form to fit the rate data of the CO2-MDEA system.
The rate constant of the reaction is given as a function of temperature by:

(3.61)
Comparison among the published values of the rate constant at 298.15 K shows a variation between 2.5 and 8.8
lit/mol/sec.

In this case the rate expression is given by:

(3.62)
Glasscock (1990) showed that this form reconciled the published rate data better.
He used activities instead of concentrations to obtain the rate constants. In the current study, the rate expression
represented by the first form (equation 3.60) with the rate constant reported by Critchfield (1988) will be used to model
the kinetics of the CO2 reaction with MDEA. The rate constant reported by Critchfield (1988) is given by:

(3.63)
2.3 CO2 Reaction with Blends of MEA-MDEA and DEA-MDEA
The absorption of CO2 in aqueous solution of blends of MEA-MDEA and DEA-MDEA was studied by Glasscock et
al. (1990), Versteeg et al. (1990), Rangwala et al. (1992), and Hagewiesche et al. (1995). Critchfield showed that the
interaction between MDEA and MEA is insignificant. Therefore the rate expressions (equation 3.37) for MEA and
(equation 3.60) for MDEA are still applicable for the mixture MEA-MDEA. However, for systems containing DEA and MDEA,
the latter acts as another base that neutralizes the zwitterion formed from the reaction of CO2 with DEA.
Hence, The CO2-DEA rate expression for systems containing DEA and MDEA should be corrected by adding the
contribution of MDEA to the neutralization of the zwitterion:
DEA/MDEA:

(3.64)

A value of 468 m6/kmol2/sec was reported in the thesis of Glasscock (1990) for the rate
constant k'R1R2R3N. In this work, this value will be used for
any temperature to compute the absorption rate of CO2in systems containing blends of DEA and MDEA.
Following the suggestion of Glasscock (1990), the effect of MDEA on the rate of reaction of CO2with MEA
will be ignored.
|
|
The rate expression in this case reduces to:

(3.60)
This form is essentially the expression, which would have been obtained if the second mechanism were used.
Many investigators including Haimor et al. (1987), Critchfield (1988), Tomcej et al. (1989), Little et al. (1990),
Rangwala et al. (1992), and Ko and Li (2000) adopted this form to fit the rate data of the CO2-MDEA system.
The rate constant of the reaction is given as a function of temperature by:

(3.61)
Comparison among the published values of the rate constant at 298.15 K shows a variation between 2.5 and 8.8
lit/mol/sec.

In this case the rate expression is given by:

(3.62)
Glasscock (1990) showed that this form reconciled the published rate data better.
He used activities instead of concentrations to obtain the rate constants. In the current study, the rate expression
represented by the first form (equation 3.60) with the rate constant reported by Critchfield (1988) will be used to model
the kinetics of the CO2 reaction with MDEA. The rate constant reported by Critchfield (1988) is given by:

(3.63)
2.3 CO2 Reaction with Blends of MEA-MDEA and DEA-MDEA
The absorption of CO2 in aqueous solution of blends of MEA-MDEA and DEA-MDEA was studied by Glasscock et
al. (1990), Versteeg et al. (1990), Rangwala et al. (1992), and Hagewiesche et al. (1995). Critchfield showed that the
interaction between MDEA and MEA is insignificant. Therefore the rate expressions (equation 3.37) for MEA and
(equation 3.60) for MDEA are still applicable for the mixture MEA-MDEA. However, for systems containing DEA and MDEA,
the latter acts as another base that neutralizes the zwitterion formed from the reaction of CO2 with DEA.
Hence, The CO2-DEA rate expression for systems containing DEA and MDEA should be corrected by adding the
contribution of MDEA to the neutralization of the zwitterion:
DEA/MDEA:

(3.64)

A value of 468 m6/kmol2/sec was reported in the thesis of Glasscock (1990) for the rate
constant k'R1R2R3N. In this work, this value will be used for
any temperature to compute the absorption rate of CO2in systems containing blends of DEA and MDEA.
Following the suggestion of Glasscock (1990), the effect of MDEA on the rate of reaction of CO2with MEA
will be ignored.
|
|
(3.60) |
This form is essentially the expression, which would have been obtained if the second mechanism were used.
Many investigators including Haimor et al. (1987), Critchfield (1988), Tomcej et al. (1989), Little et al. (1990),
Rangwala et al. (1992), and Ko and Li (2000) adopted this form to fit the rate data of the CO2-MDEA system.
The rate constant of the reaction is given as a function of temperature by:

(3.61)
Comparison among the published values of the rate constant at 298.15 K shows a variation between 2.5 and 8.8
lit/mol/sec.

In this case the rate expression is given by:

(3.62)
Glasscock (1990) showed that this form reconciled the published rate data better.
He used activities instead of concentrations to obtain the rate constants. In the current study, the rate expression
represented by the first form (equation 3.60) with the rate constant reported by Critchfield (1988) will be used to model
the kinetics of the CO2 reaction with MDEA. The rate constant reported by Critchfield (1988) is given by:

(3.63)
2.3 CO2 Reaction with Blends of MEA-MDEA and DEA-MDEA
The absorption of CO2 in aqueous solution of blends of MEA-MDEA and DEA-MDEA was studied by Glasscock et
al. (1990), Versteeg et al. (1990), Rangwala et al. (1992), and Hagewiesche et al. (1995). Critchfield showed that the
interaction between MDEA and MEA is insignificant. Therefore the rate expressions (equation 3.37) for MEA and
(equation 3.60) for MDEA are still applicable for the mixture MEA-MDEA. However, for systems containing DEA and MDEA,
the latter acts as another base that neutralizes the zwitterion formed from the reaction of CO2 with DEA.
Hence, The CO2-DEA rate expression for systems containing DEA and MDEA should be corrected by adding the
contribution of MDEA to the neutralization of the zwitterion:
DEA/MDEA:

(3.64)

A value of 468 m6/kmol2/sec was reported in the thesis of Glasscock (1990) for the rate
constant k'R1R2R3N. In this work, this value will be used for
any temperature to compute the absorption rate of CO2in systems containing blends of DEA and MDEA.
Following the suggestion of Glasscock (1990), the effect of MDEA on the rate of reaction of CO2with MEA
will be ignored.
|
|
(3.61) |
Comparison among the published values of the rate constant at 298.15 K shows a variation between 2.5 and 8.8
lit/mol/sec.

In this case the rate expression is given by:

(3.62)
Glasscock (1990) showed that this form reconciled the published rate data better.
He used activities instead of concentrations to obtain the rate constants. In the current study, the rate expression
represented by the first form (equation 3.60) with the rate constant reported by Critchfield (1988) will be used to model
the kinetics of the CO2 reaction with MDEA. The rate constant reported by Critchfield (1988) is given by:

(3.63)
2.3 CO2 Reaction with Blends of MEA-MDEA and DEA-MDEA
The absorption of CO2 in aqueous solution of blends of MEA-MDEA and DEA-MDEA was studied by Glasscock et
al. (1990), Versteeg et al. (1990), Rangwala et al. (1992), and Hagewiesche et al. (1995). Critchfield showed that the
interaction between MDEA and MEA is insignificant. Therefore the rate expressions (equation 3.37) for MEA and
(equation 3.60) for MDEA are still applicable for the mixture MEA-MDEA. However, for systems containing DEA and MDEA,
the latter acts as another base that neutralizes the zwitterion formed from the reaction of CO2 with DEA.
Hence, The CO2-DEA rate expression for systems containing DEA and MDEA should be corrected by adding the
contribution of MDEA to the neutralization of the zwitterion:
DEA/MDEA:

(3.64)

A value of 468 m6/kmol2/sec was reported in the thesis of Glasscock (1990) for the rate
constant k'R1R2R3N. In this work, this value will be used for
any temperature to compute the absorption rate of CO2in systems containing blends of DEA and MDEA.
Following the suggestion of Glasscock (1990), the effect of MDEA on the rate of reaction of CO2with MEA
will be ignored.
|
|
In this case the rate expression is given by:

(3.62)
Glasscock (1990) showed that this form reconciled the published rate data better.
He used activities instead of concentrations to obtain the rate constants. In the current study, the rate expression
represented by the first form (equation 3.60) with the rate constant reported by Critchfield (1988) will be used to model
the kinetics of the CO2 reaction with MDEA. The rate constant reported by Critchfield (1988) is given by:

(3.63)
2.3 CO2 Reaction with Blends of MEA-MDEA and DEA-MDEA
The absorption of CO2 in aqueous solution of blends of MEA-MDEA and DEA-MDEA was studied by Glasscock et
al. (1990), Versteeg et al. (1990), Rangwala et al. (1992), and Hagewiesche et al. (1995). Critchfield showed that the
interaction between MDEA and MEA is insignificant. Therefore the rate expressions (equation 3.37) for MEA and
(equation 3.60) for MDEA are still applicable for the mixture MEA-MDEA. However, for systems containing DEA and MDEA,
the latter acts as another base that neutralizes the zwitterion formed from the reaction of CO2 with DEA.
Hence, The CO2-DEA rate expression for systems containing DEA and MDEA should be corrected by adding the
contribution of MDEA to the neutralization of the zwitterion:
DEA/MDEA:

(3.64)

A value of 468 m6/kmol2/sec was reported in the thesis of Glasscock (1990) for the rate
constant k'R1R2R3N. In this work, this value will be used for
any temperature to compute the absorption rate of CO2in systems containing blends of DEA and MDEA.
Following the suggestion of Glasscock (1990), the effect of MDEA on the rate of reaction of CO2with MEA
will be ignored.
|
|
(3.62) |
Glasscock (1990) showed that this form reconciled the published rate data better.
He used activities instead of concentrations to obtain the rate constants. In the current study, the rate expression
represented by the first form (equation 3.60) with the rate constant reported by Critchfield (1988) will be used to model
the kinetics of the CO2 reaction with MDEA. The rate constant reported by Critchfield (1988) is given by:

(3.63)
2.3 CO2 Reaction with Blends of MEA-MDEA and DEA-MDEA
The absorption of CO2 in aqueous solution of blends of MEA-MDEA and DEA-MDEA was studied by Glasscock et
al. (1990), Versteeg et al. (1990), Rangwala et al. (1992), and Hagewiesche et al. (1995). Critchfield showed that the
interaction between MDEA and MEA is insignificant. Therefore the rate expressions (equation 3.37) for MEA and
(equation 3.60) for MDEA are still applicable for the mixture MEA-MDEA. However, for systems containing DEA and MDEA,
the latter acts as another base that neutralizes the zwitterion formed from the reaction of CO2 with DEA.
Hence, The CO2-DEA rate expression for systems containing DEA and MDEA should be corrected by adding the
contribution of MDEA to the neutralization of the zwitterion:
DEA/MDEA:

(3.64)

A value of 468 m6/kmol2/sec was reported in the thesis of Glasscock (1990) for the rate
constant k'R1R2R3N. In this work, this value will be used for
any temperature to compute the absorption rate of CO2in systems containing blends of DEA and MDEA.
Following the suggestion of Glasscock (1990), the effect of MDEA on the rate of reaction of CO2with MEA
will be ignored.
|
|
(3.63) |
2.3 CO2 Reaction with Blends of MEA-MDEA and DEA-MDEA
The absorption of CO2 in aqueous solution of blends of MEA-MDEA and DEA-MDEA was studied by Glasscock et
al. (1990), Versteeg et al. (1990), Rangwala et al. (1992), and Hagewiesche et al. (1995). Critchfield showed that the
interaction between MDEA and MEA is insignificant. Therefore the rate expressions (equation 3.37) for MEA and
(equation 3.60) for MDEA are still applicable for the mixture MEA-MDEA. However, for systems containing DEA and MDEA,
the latter acts as another base that neutralizes the zwitterion formed from the reaction of CO2 with DEA.
Hence, The CO2-DEA rate expression for systems containing DEA and MDEA should be corrected by adding the
contribution of MDEA to the neutralization of the zwitterion:
DEA/MDEA:

(3.64)

A value of 468 m6/kmol2/sec was reported in the thesis of Glasscock (1990) for the rate
constant k'R1R2R3N. In this work, this value will be used for
any temperature to compute the absorption rate of CO2in systems containing blends of DEA and MDEA.
Following the suggestion of Glasscock (1990), the effect of MDEA on the rate of reaction of CO2with MEA
will be ignored.
| DEA/MDEA: |
|
(3.64) |

|
||