Вернуться в библиотеку

УДК 669.14.1

ОБОСНОВАНИЕ СТРУКТУРЫ МОДЕЛИ ПРОЦЕССА КРИСТАЛЛИЗАЦИИ ЗАГОТОВКИ ПРИ УПРАВЛЕНИИ МНЛЗ

Бобита Т.Ю., студентка,  Маренич К.Н., Ph. D. (к.т.н.), доцент

(Донецкий национальный технический университет, г. Донецк, Украина)

Автоматизация технологических объектов и процессов.  Сборник научных трудов. VІІ Международная начно-техническая конференция аспирантов и студентов в г. Донецке 26 -28 апреля 2007г. – Донецьк: ДонНТУ, 2007, с.293 - (с. 93 - 95).

         Для достижения высокой производительности МНЛЗ и получения качественных слитков необходимо установить связь технологии с тепловой работой машины.

         Подавляющее большинство МНЛЗ оснащено нерегулируемым по скорости электроприводом на основе синхронного двигателя. Наиболее эффективное автоматическое управление процессом непрерывной разливки будет достигнуто применением тиристорно-управляемых асинхронных двигателей с короткозамкнутым ротором. Это имеет практическое значение для для случев пуска машины и набора скорости разливки, переходе с плавки на плавку, временного снижения или повышения скорости, аварийной остановки и т.д. Поэтому актуальным является исследование зависимости процесса теплопередачи и затвердевания слитка от режимных, конструктивных и технологических параметров.    

         Практическая задача определения динамики  затвердевания расплава, включающая определение температурного поля, скорости продвижения фронта кристаллизации, времени полного затвердевания слитка и глубины жидкой фазы решается современными средствами математического моделирования с достаточной для практических целей точностью.

         С целью определения параметров твердожидкой зоны, а также решения ряда практических вопросов, связанных с формированием слитка, используют задачу о нахождении температурного поля в затвердевающем слитке:  

   где температура разливки, ˚С;

        скорость разливки, м/мин;     

        сечение заготовки, м;

        соответственно теплопроводность [Вт/м˚С], теплоёмкость [кДж/кг˚С] и плотность [кг/м³] опре  делённой марки стали;

      расходы первичной и вторичной охлаждающей воды, м³/с.

   При построении математической модели сделаны следующие допущения: процесс формирования слитка является установившимся, перенос тепла вдоль оси (в направлении вытягивания ) пренебрежимо мал по сравнению с переносом тепла в поперечных направлениях;  перемешивание жидкого металла внутри слитка не учитывается, слиток считается сплошной однородной средой, начало координат движется вниз вместе со слитком с постоянной скоростью, равной скорости вытягивания, температурное поле симметрично относительно осей координат, для задания граничных условий вдоль технологической оси слитка выделяются такие  характерные зоны:  кристаллизатор, зона вторичного охлаждения, зона свободного охлаждения.           

          В основу математической модели положено дифференциальное уравнение теплопроводности (1) с учётом скрытой теплоты кристаллизации, которая определялась по линейному закону в соответствии с правилом рычага введением эффективной теплоёмкости С_э(Т), величина которой задаётся в интервале температур ликвидус-солидус в виде системы:

          где  субстанциальная производная температуры;

          Пределы изменения координат составили 0<x<l_ш ; 0<y<l_у , где l_ш и l_у – соответственно ширина половины широкой и узкой граней слитка. Начальные условия: , где  начальная температура металла. Наиболее эффективным является использование для описания теплообмена между заготовкой и охлаждающей средой граничных условий третьего рода..

   Для учёта конвективного переноса вводится коэффициент теплопроводности   (Т):

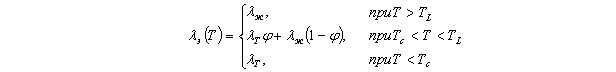
          где величина относительного количества твёрдой фазы ( для жидкой фазы, для полностью затвердевшей части слитка и для двухфазной зоны может изменяться от нуля до единицы);    соответственно объёмы всего расплава и твёрдой фазы.

 Плотность стали определяется в зависимости от температуры и усредняется в двухфазной зоне:

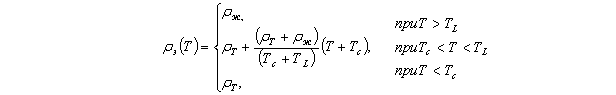
 Вышеприведенные системы уравнений вместе с условиями однозначности представляют собой полную формулировку математической модели процесса затвердевания непрерывного слитка.

 Решение этой системы позволяет определить температурное поле непрерывного слитка в любой момент времени от начала формирования оболочки слитка на уровне металла в кристаллизаторе, а также исследовать влияние внешних условий на тепловой режим формирования слитка.

     Перечень ссылок:

1. Тепловая работа непрерывного литья заготовок. Емельянов В.А. Учебное пособие для ВУЗов. - М.: Металлургия, 1988. - 143с.

2. Самойлович Ю.А. Микрокомпьютер в решении задач кристаллизации слитка. - М.: Металлургия, 1988. -182с.

3. Евтеев Д.П., Колыбалов И.Н. Непрерывное литьё стали. - М.: Металлургия, 1984. - 200с.

Вернуться в библиотеку