|
|
|
|
| Биография | Отчет о поиске | Автореферат | Ссылки | Библиотека | Индивидуальное задание |
Одними из основных задач при построении САУ нагревательными колодцами является разработка компьютерной математической модели нагрева слитков, обоснование ее коррекции и адекватности реальному объекту, так как модель дает возможность осуществлять в реальном масштабе времени автоматический расчетный контроль технологических параметров, недоступных для прямого инструментального контроля.
В качестве входных переменных математической модели выступают: производительность печи, общий расход топлива на печь.
В качестве выходных переменных, значения которых определяются в результате расчета, могут выступать температура поверхности слитка и перепад температур по его сечению на выходе из печи, температура продуктов сгорания, покидающих рабочее пространство.
При разработке модели будут сделаны следующие ограничения и допущения:
- скорость увеличения температуры рабочего пространства колодца в период подъема температуры ограничена тепловой мощностью ячейки:
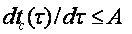
- максимальная температура рабочего пространства ограничена стойкостью огнеупорной кладки колодца:
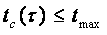
- предельная температура поверхности слитков не должна превышать температуры пережога данной марки стали:
Исследования, проведенные на одном из металлургических заводов, показали, что температуру поверхности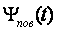 
и среднюю интегральную температуру слитков 
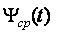можно рассчитать по температуре рабочего пространства ячейки 
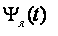, решая упрощенное дифференциальное уравнение вида:
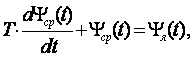
где Т – постоянная времени нагрева, равная 100-200 мин [1], возрастает с увеличением садки и размеров слитков и определяется экспериментально.
На рисунке 1а представлена структурная модель нагревательного колодца, а на рисунке 1б – расчетная схема.
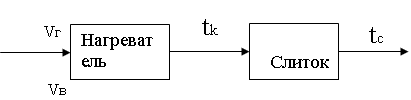
Выведем передаточную функцию объекта регулирования (нагреваемого слитка) из уравнения нагрева слитка (1). При введении следующих замен 
, 
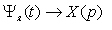и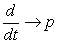 
получим 
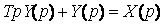. Поскольку передаточная функция имеет известный вид, то передаточная функция нагреваемого слитка имеет вид апериодического звена первого порядка:
Термопара в системе автоматического регулирования представлена звеном запаздывания с передаточной функцией [2]:
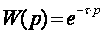
Объект регулирования имеет следующие параметры: Т=230 мин,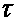 
=60 c [1].
По графику переходного процесса можем сделать вывод о том, что структура исследуемого объекта требует коррекции, т.к. выходная величина, а именно температура нагреваемого слитка, достигает установившегося значения через достаточно длительный промежуток времени.
С целью коррекции структуры объекта в структурную схему необходимо ввести регулятор температуры в рабочем пространстве. В период нагрева, когда температура ниже заданной, регулятор будет полностью открывать регулирующий орган, подавая в печь максимальное количество тепла. В период прогрева (томления) температура достигает заданного значения и регулятор поддерживает ее, уменьшая расход топлива. Таким образом, будет достигнуто оптимальное управление процессом нагрева стальных слитков в нагревательных колодцах, в частности сократится время нагрева, а следовательно, уменьшится расход топлива и воздуха.
| ДонНТУ | Портал магистров ДонНТУ | Библиотека | Биография | Отчет о поиске | Автореферат | Ссылки | Индивидуальное задание |