Cavitation in Control Valves
Cavitation has been a familiar phenomenon for a long time particularly in shipping. In 1917, the British physicist Lord Rayleigh was asked to investigate what caused fast-rotating ship propellers to erode so quickly. He discovered that the effect of cavitation, already proved in experiments by Reynolds in 1894, was the source of the problem. Despite numerous investigations into the subject of cavitation in the years that followed, many of the accompanying effects have still not yet been completely explained. This is no wonder considering the complexity of the process involving the areas of acoustics, hydrodynamics, thermodynamics, optics, plasma physics and chemistry.
Cavitation can be caused in a fluid by energy input. For example, a laser beam creates a plasma in liquids which causes the liquid to evaporate creating a cavity. Ultrasonic waves can be used to induce complex high-frequency alternating compression and rarefaction phases in liquids which cause cavitation. In this way, cavitation effects can be applied usefully for cleaning surfaces, for non-invasive operations in the field of medicine and for breaking down agglomerates in the textile finishing industry. In sewage treatment plants, cavitation is used to break down molecules and bacteria cell walls, break up pollutants and dissolve out minerals from organic material.
Furthermore, cavitation can arise in hydrodynamic flows when the pressure drops. This effect is, however, regarded to be a destructive phenomenon for the most part. In addition to pump rotors, control valves are particularly exposed to this problem since the static pressure at the vena contracta even at moderate operating conditions can reach levels sufficient for cavitation to start occurring in liquids.
The consequences for a control valve as well as for the entire control process vary and are often destructive:
- Loud noise
- Strong vibrations
- Choked flow caused by vapor
- Change of fluid properties
- Erosion of valve components
- Destruction of the control valve
- Plant shutdown
Cavitation
Cavitation shall be generally understood as the dynamic process of the formation and implosion of cavities in fluids. Cavitation occurs, for instance, when high flow velocities cause the local hydrostatic pressure to drop to a critical value which roughly corresponds to the vapor pressure of the fluid. This causes small bubbles filled with steam and gases to form. These bubbles finally collapse when they reach the high-pressure areas as they are carried along by the liquid flow. In the final phase of bubble implosion, high pressure peaks are generated inside the bubbles and in their immediate surroundings.
These pressure peaks lead to mechanical vibrations, noise and material erosion of surfaces in walled areas. If cavitation is severe, the hydraulic valve coefficients as well as the fluid properties change.
Incipient cavitation
The term ‘cavitation’ is derived from the Latin verb cavitare meaning ‘to hollow out’, thus referring to the formation of cavities. To create cavities in fluids, the fluid must first be expanded and then ruptured. Theoretically, fluids can absorb high tensile strengths or negative pressures. Ackeret [1] estimates the negative pressure required to cause cavitation in pure water at 20 ºC, based on the minimum of the van der Waals curve, and receives a theoretically possible tensile strength of 104 bar which corresponds approximately to the reciprocal compressibility of water.
The tensile strength of the medium is reduced by the disturbance
Inhomogeneities (disturbances) in the quasi-crystalline structure of water, however, reduce the possible tensile strengths by minimum one order of magnitude. In all probability, submicroscopic accumulations of steam or gas molecules are created at these disturbances with the molecules being in an unstable equilibrium with the fluid. In the case of external tensile strengths (negative pressure), these nuclei can exceed a critical diameter and then grow spontaneously as steam is formed.
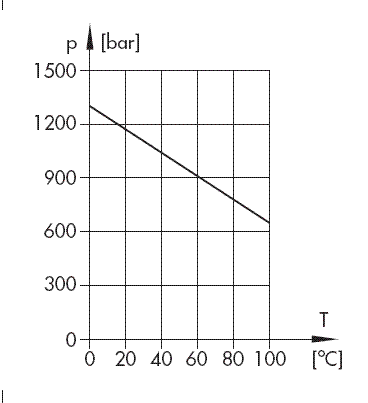
Fig. 1: Theoretical tensile strength values for perfect water
By means of statistical examination, Becker and Doring determined the probability for a critical nucleus to occur in dependence of the temperature, resulting in the theoretical tensile strength values for perfect water shown in Fig. 1.
If these values were actually reached for industrial fluids, cavitation in connection with hydraulic systems would not be a matter for discussion. The highest values known until now were derived by measuring centrifugal force as a function of the temperature with extremely pure water. As shown in Fig. 2, the highest value to be achieved was only at 280 bars. Fig. 2 also shows one of the many anomalies of water, i.e. the strong reduction of tensile strength near the freezing point which is caused by the formation of water crystals.
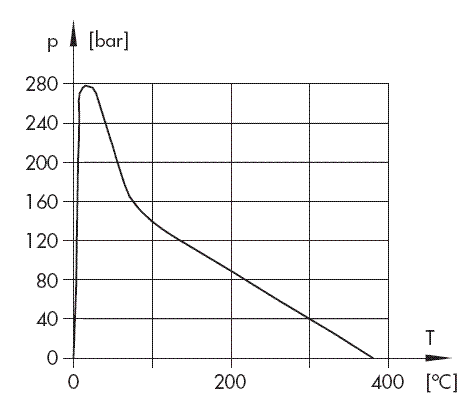
Fig. 2: Tensile strength values derived from measurements for pure water
Cavitation nuclei are decisive for the occurrence of cavitation
The discrepancy between the theoretically and experimentally (under ideal conditions) determined strength values shows that the microscopic bubbles filled with gas and steam (cavitation nuclei), which exist in the fluid and whose existence in water can be explained according to the model by Harvey, are a decisive factor in the occurrence of cavitation.
Spherical cavitation nuclei are stable when the fluid pressure p acting on the bubble surface and the partial pressure 2α/ R resulting from the surface tension are in equilibrium with the sum of the partial pressures inside the bubble, i.e. the vapor pressure pV and the pressure of the enclosed gas volume pG:

In this equation, R is the radius of the bubble and ??is the capillary constant. If you consider the volume change of the bubble to be isothermal, the following can be derived from the general gas law for spherical nuclei:
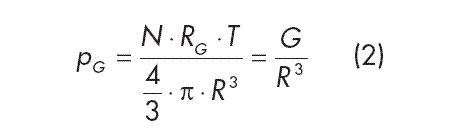
and with (1)
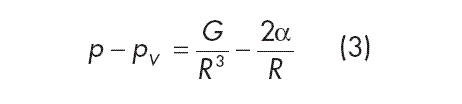
with G being proportional to the gas volume contained in the nucleus.
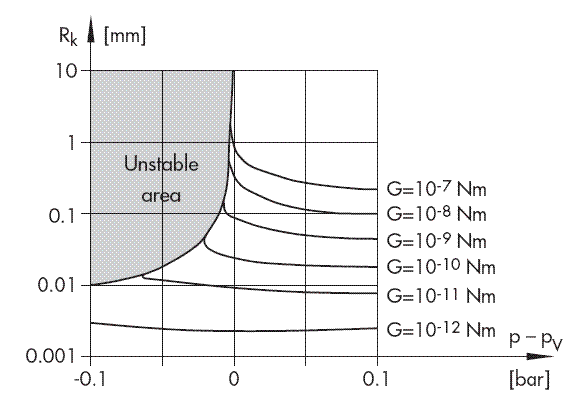
Fig. 3: Critical nucleus radius with varying gas concentrations
The representation p – pV = f(R) with G as a parameter exemplifies incipient cavitation: (Fig. 3).
When parameters are fixed, at first the radius of the nucleus will increase only slowly as the static pressure decreases. A small change in pressure only results in unlimited bubble growth, i.e. incipient cavitation, after a critical pressure difference has been reached which is mathematically defined by d(p – pV)/dR = 0 and which is derived from:
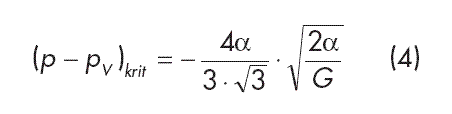
Large nuclei, i.e. bubbles with a large G value, start to cavitate first. Their sudden growth accelerates the ambient fluid and reduces the pressure locally. This pressure reduction causes the next smaller bubbles to collapse, which in turn build up a pressure field that causes even smaller bubbles to collapse, and so forth.
Incipient cavitation starts just below vapor pressure
As a result, the critical pressure at which cavitation stops is higher than the critical pressure at incipient cavitation. Lehmann and Young examined the phenomenon of cavitation hysteresis in depth and found that the end of cavitation can be more easily reproduced than incipient cavitation. In particular cases, it therefore depends on the state of the liquid, especially the temperature, spectrum of nuclei, the content of dissolved gases and the surface tension, at which static pressure cavitation begins. Generally, this is just below the vapor pressure. In practice, it is impossible to determine a liquid’s spectrum of nuclei in advance for most applications. Therefore, it is common practice in control valve sizing to describe the critical state of the cavitation nuclei at incipient cavitation by means of the vapor pressure of the liquid.
The cavitation coefficient xFZ
In the case of less viscous liquid flows around streamlined bodies, the internal friction compared to the pressure may be frequently neglected. The velocity distribution of these types of flow can be calculated on the basis of the potential theory if the flow conditions are known. The pressure distribution along the body contour is derived from Bernoulli’s equation so that a relationship between the minimum pressure pmin and the critical pressure can be stated according to equation (4).