Источник: Синхронизация времени в распределенном имитационном моделировании
А.И. Миков , Е.Б. Замятина. Распределенные системы и алгоритмы.
Управление временем в распределенном моделировании
Управление временем в распределённом моделировании должно обеспечивать выполнение событий в правильном хронологическом порядке. Более того, на алгоритмы синхронизации возлагается обязанность корректно выполнять повторные имитационные прогоны. При повторном моделировании пользователь должен быть уверен, что он получит те же результаты, что и в первый раз, если входные данные останутся неизменными. Обеспечение следования событий в правильном порядке и проблемы повторного имитационного прогона для моделирования тренажёров несущественно. Поэтому речь о дискретно-событийном моделировании.
Сделаем предположение, что имитационная модель представляет собой совокупность логических процессов (LPi), которые взаимодействуют друг с другом, посылая друг другу сообщения с временной меткой (time stamped) или события. Логические процессы являются отражением физических процессов PPj. События логического процесса должны выполняться в хронологическом порядке. Это требование называют ограничением локальной каузальности (local causality constraint). Можно показать, что если игнорировать события с одинаковыми временными метками и если процесс поддерживает ограничение локальной каузальности, то выполнение имитационной программы на параллельном компьютере даст такие же результаты, как и выполнение на последовательном, где все события выполняются в соответствии с их временными метками. Кроме того, это свойство позволяет убедиться в том, что выполнение имитационного прогона повторяемо (даёт те же результаты при одном и том же наборе исходных данных).
Будем рассматривать каждый логический процесс как последовательный симулятор, поддерживающий дискретное событийное моделирование. А это означает, что каждый логический процесс содержит локальную информацию о состоянии объектов моделирования и список событий, которые были запланированы для этого процесса, но ещё не были выполнены (pending event list). Этот список необработанных событий включает локальные события (т.е. запланированные самим процессом LPi) и события, запланированные для него другими процессами.
Работа симулятора заключается в том, чтобы выбрать из списка необработанных событий событие с минимальной временной меткой и обработать его. Так выполнение процесса можно рассматривать как выполнение последовательности событий. Выполнение событие сопровождается изменением переменных, которые определяют состояние моделируемого объекта. Кроме того, логический процесс при выполнении очередного события может запланировать выполнение нового события ej для самого себя или для другого логического процесса. Каждый логический процесс имеет локальные часы. Локальные часы указывают на время выполнения самого последнего обработанного симулятором события. Время, на которое запланировано логическим процессом любое событие должно быть больше, чем значение его локальных часов.
Итак, m = {LP, ME}, где LP – это множество процессов, ME – коммуникационная среда для передачи сообщений от одного процесса другому. В свою очередь,
LPi = {Q, E, Sch, Ch, T}, где
T – линейно-упорядоченное абстрактное множество с отношением порядка \le. Множество T называют множеством моментов времени.
Q – множество состояний,
E – множество событий, E =Ein ![]() Em.
Em.
Ein – это множество внутренних событий процесса.
Em –множество событий, полученных процессом i процессом от j-того процесса. Если процесс LPi получит сообщение (событие, которое запланировано для него процессом LPj ), то он должен переупорядочить очередь локальных событий (или календарь событий) C = ((e1, t1), (e2 , t2),…,(en , tn)), включив в неё пару (ej , tj). Очередь С упорядочена по возрастанию временных меток событий.
Sch – преобразование планирования событий процесса ei, Sch: E x Q x T ![]() E;
E;
Ch – преобразование изменения состояния Сh: E x Q x T ![]() Q,
Q,
Tloc – локальное время логического процесса (время последнего обработанного события из множества E).
Текущее модельное время time = min(Tloci), i = 1 ÷ n.
Парадоксы времени
Алгоритм управления временем должен следить за тем, чтобы события выполнялись в хронологическом порядке. Эта задача не является тривиальной. Действительно, логический процесс заранее не может знать о том, на какое время будет запланировано событие, которое он получает от другого логического процесса. Пусть в списке необработанных событий хранится событие с временной меткой 10. Может ли симулятор логического процесса выбрать его для обработки. Это можно было бы сделать, если бы логический процесс каким-нибудь образом знал о том, что другой логический процесс не запланировал для него события, со временем меньшим, чем 10.
Рассмотрим другой пример.
Пусть модель представляет собой совокупность трёх процессов. Один процесс отображает поведение покупателя, второй – магазина, в котором покупатель совершает покупки, а третий процесс – деятельность банка, со счёта которого покупатель снимает деньги.
Предположим, что покупатель приобрёл товары в магазине на определённую сумму N (в кредит) (событие e1, произошло в момент времени t1 = 9). Магазин уведомил об этом банк (e2, t2 = 10) Сумма на счёте уменьшается: S = S – N. Покупатель посещает банк с целью снять деньги со счёта (e3, t3=11). Если денег на счёте достаточно, то банк выдаёт клиенту (которым является покупатель) запрошенную им сумму. Если счёт меньше запрошенной суммы, то покупателю будет отказано.
Хронологический порядок событий: e1, e2, e3 (рис. 8.1).
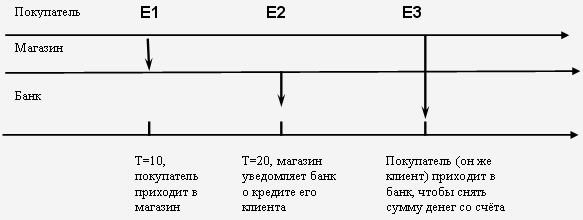
Рис. 8.1. Банк получает сообщения в хронологическом порядке
Рассмотрим описанную выше ситуацию: если уведомление в банк из магазина поступит позже того, как покупатель снимет сумму с вклада в банке (которой уже нет на счёте), то банк понесёт убытки. Ситуация, которая обрисована выше, возникла вследствие того, что хронология событий была нарушена (рис. 8.2).
Нарушение хронологического порядка могло произойти по той причине, что в распределённом моделировании время для разных логических процессов движется с разной скоростью. Например, если процесс, реализующий работу магазина, выполняется на загруженном процессоре, то уведомление банку поступает позже, поскольку процесс банк "убежал" вперёд (он выполняется на менее загруженном процессоре).
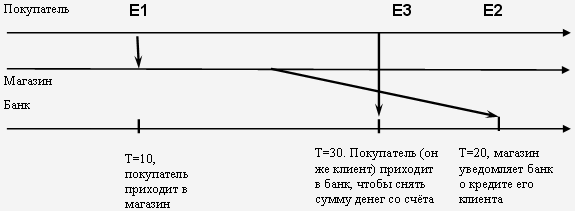
Рис. 8.2. Хронологический порядок событий нарушен
Распределённый алгоритм должен уметь бороться с такими парадоксами времени.
В этом и заключается проблема синхронизации компонентов распределённого моделирования. Было предпринято множество попыток решить эту проблему. В настоящее время все алгоритмы синхронизации делятся на консервативные и оптимистические.
Если мы вернёмся к примеру 1, то консервативный алгоритм не позволит логическому процессу обрабатывать событие с временной отметкой 10, пока не убедится, что другой логический процесс не запланировал для него события с временной меткой, меньшей 10.
Оптимистический алгоритм позволяет выбирать из списка необработанных событий очередное событие и обрабатывать его, исключив проверку событий, планируемых другими логическими процессами. Однако отдельный программный механизм реализует обнаружение ошибок и восстановление от ошибок выполнения событий, которые происходят не в хронологическом порядке.
Рассмотрим более подробно каждый из алгоритмов управления временем.
Консервативное управление временем
Первые алгоритмы синхронизации использовали консервативный подход. Принципиальная задача консервативного протокола – определить время, когда обработка очередного события из списка необработанных событий является "безопасным". Иными словами, событие является безопасным, если можно гарантировать, что процесс в дальнейшем не получит от других процессов событие с меньшей временной меткой. Консервативный подход не позволяет выполнять событие до тех пор, пока нет гарантии, что оно является безопасным.
Большинства консервативных алгоритмов основано на вычислении LBTS (Lower Bound on the Time Stamp – нижняя граница временных меток) будущих сообщений, которые могут быть получены логическим процессом. Этот механизм позволяет определить, является ли очередной событие из списка необработанных событий безопасным. Действительно, если консервативный алгоритм определит, что LBTS = 11, то все события из списка необработанных событий с временной отметкой, меньшей 11, являются безопасными и могут быть выполнены. Соответственно, события с временной меткой, большей 11 не являются безопасными и не могут быть выполнены. Что касается событий, которые имеют временную отметку, равную 12 (LBTS = 12), то их обработка зависит от реализации конкретного консервативного алгоритма и правил, по которому должны обрабатываться события, запланированные на один и тот же момент времени (одновременные события – simultaneous events).
Будем считать, что логические процессы не содержат событий, запланированных на одно и то же модельное время.
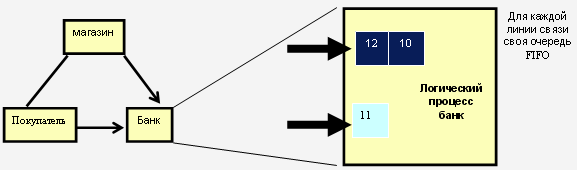
Рис. 8.3. Процесс "Банк" и очереди FIFO для каждой из линий связи
Алгоритм с нулевыми сообщениями
Первыми консервативными алгоритмами считаются алгоритмы, разработанные Bryant, Chandy, Misra.
Алгоритм предполагает:
- Топология процессов, которые посылают сообщения друг другу, известна и фиксирована.
- Каждый логический процесс посылает сообщения с неубывающими временными метками.
- Коммуникационная среда обеспечивает доставку сообщений в том порядке, в котором они были посланы.
Исходя из этих предположений, можно сделать следующее заключение:
- Временная метка сообщения, которое было получено последним на линии связи, является нижней границей временных меток (LBTS) всех будущих сообщений, передаваемых по этой линии связи.
- Нижняя временная метка (LBTS) логического процесса определяется как минимальная из всех нижних временных меток, полученных процессом по всем входным линиям связи.
Сообщения каждой линии связи находятся в очереди, которая обрабатывается по дисциплине FIFO. Очередь упорядочена также в соответствии с временными метками. Каждая линия связи имеет своё локальное время, которое равно временной отметке первого сообщения в очереди (если таковые имеются) или временной отметке последнего принятого сообщения (рис. 8.3). Все события, которые планирует сам процесс для себя, находятся в другой очереди. Алгоритм периодически выбирает линию связи с наименьшим временем и, если в ней есть события, то он обрабатывает это событие. Если очередь пуста, то процесс блокируется. Процесс никогда не блокируется при проверке состояния очереди сообщений, которые он планирует для себя. Итак, этот алгоритм гарантирует, что каждый логический процесс будет обрабатывать события в хронологическом порядке.
Цель: Необходимо, чтобы события выполнялись в хронологическом порядке:
while (не конец моделирования) do
begin
Ждать пока каждая из очередей содержит хотя бы одно сообщение
Удалить сообщение с наименьшей меткой, просмотрев каждую из очередей.
Обработать это событие
end
Вернёмся к примеру: В очередях последовательно были обработаны события, запланированные на время t1=10, t2=11. Далее процесс ожидает появления сообщения от покупателя. Иначе он не может продолжить работу. Процесс блокируется (рис. 8.4).
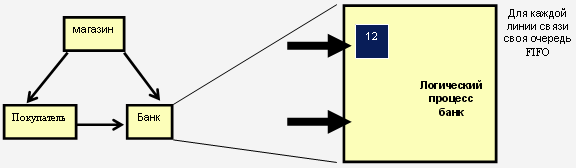
Рис. 8.4. Процесс блокируется, потому что на линии связи с процессом-покупателем нет сообщений
Несмотря на то, что алгоритм обеспечивает локальную каузальность, при его выполнении могут возникнуть тупики. Действительно, если нижняя граница временных отметок на всех линиях связи будет меньше, чем необработанные события, то это приведет к ожиданию выполнения другого цикла.
Пример:
Итак, у нас 3 процесса LP1, LP2, LP3. Процесс LP1 блокирован, т.к. ожидает прихода сообщения от LP3 и не может отослать сообщения процессу LP2. Процесс LP2 тоже блокирован, он ожидает сообщений от LP1. Процесс LP3 в свою очередь блокирован, поскольку в его входной очереди нет сообщений от первого процесса LP1. Теперь мы видим, что происходит циклическое ожидание процессов (тупик). Иллюстрацию примера см. на рис.
Для того, чтобы избежать возникновение тупиков, Chandy и Misra предложили использовать нулевые сообщения. Процесс LPa посылает сообщение с временной меткой Tnull процессу LPb. Этим процесс LPa сообщает процессу LPb, что он не пришлёт процессу сообщение с временной отметкой, меньшей, чем Tnull. Нулевые сообщения не соответствуют каким-либо физическим явлениям моделируемого объекта.
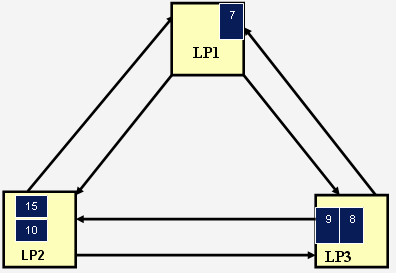
Рис. 8.5. Циклическое ожидание процессов
Процессы отсылают нулевые сообщения по всем выходным дугам после обработки очередного события. Нулевое сообщение служит дополнительной информацией для того, чтобы определить очередное безопасное событие.
Нулевое сообщение обрабатывается как обычное сообщение за исключением того факта, что ни одна переменная процесса и никакое событие не будут запланированы. Локальное время логического процесса продвигается до временной отметки нулевого сообщения.
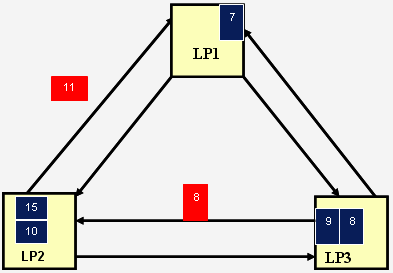
Рис. 8.6. Отсылка по выходным дугам нулевых сообщений
Каким образом процесс определит временную метку нулевого сообщения, которое он отсылает?
Значение часов каждой линии связи определяет нижнюю границу временной метки следующего события, которое будет извлечено из буфера этой линии связи. Эта нижняя граница в совокупности со сведениями о выполнении процесса являются исходной информацией для определения нижней границы временных меток для всех посылаемых с выходных дуг сообщений. Fujimoto приводит такой пример: если известно, что некоторое обслуживающее устройство обрабатывает заявку в течении T единиц модельного времени, то временная метка любого отсылаемого сообщения по крайней мере на T единиц модельного времени больше, нежели временная метка любого сообщения, которое может появиться в будущем (рис. 8.5).
Как только процесс завершит обработку нулевого или ненулевого сообщения, он вновь посылает нулевое сообщение по выходным дугам. Процесс, получивший нулевое сообщение, обязан вычислить нижнюю границу временной метки и отослать эту информацию свои соседям и т.д.
Алгоритм с нулевыми сообщениями (выполняется каждым логическим процессом LP):
Цель: Обеспечить выполнение событий в хронологическом порядке и избежать тупиков
while (не конец моделирования) do
begin
Ждать пока не выполнится условие: каждая очередь FIFO
содержит хотя бы одно сообщение.
Удалить событие с наименьшей временной отметкой из FIFO.
Обработать это событие.
Послать нулевое сообщение своим соседям с временной меткой,
указывающей нижнюю границу будущих событий, посланных этому LP
(текущее время + lookahead)
end
Итак, приведённый выше алгоритм с использованием нулевых сообщений позволяет избавиться от тупиков.
Использование lookahead (Забегания вперёд)
Для консервативных алгоритмов синхронизации характерной особенностью является использование предварительного просмотра (lookahead).
Предположим, что некоторый логический процесс имеет локальное время с отметкой T. Процесс может гарантировать, что любое будущее сообщение, отосланное им, будет иметь временную метку, превосходящую временную метку пришедшего позднее сообщения, на величину, равную T+L. В этом случае говорят, что процесс имеет предварительный просмотр величиной, равной L. Предварительный просмотр используют для того, чтобы вычислить временную метку нулевого сообщения. Величина предварительного просмотра указывает на то, что на протяжении некоторого временного отрезка L исходящих сообщений не будет.
Обсуждаемый алгоритм допускает множество модификаций, таких как, например, подсчёт lookahead по отдельности для различных исходящих дуг, что приводит к значительному уменьшению простоя логических процессов. К отрицательным характеристикам этого алгоритма можно отнести тот факт, что если процессы сильно связаны, то все логические процессы будут продвигаться лишь на очень малые промежутки времени. Таким образом, моделирование по своей сути будет последовательным. Недостатком алгоритма является и то, что при небольших значениях lookahead возможна ситуация циклического ожидания нескольких LP с небольшими продвижениями локальных часов. В некоторых системах возможно, а зачастую и необходимо, использование нулевого предварительного просмотра (zero lookahead), однако обсуждаемый выше алгоритм не допускает нулевых предварительных просмотров.
Использование дополнительной информации о временной метке следующего события
Рассмотрим подробнее недостатки алгоритмы с нулевыми сообщениями. Итак, одним из недостатков алгоритма является тот факт, что он может сгенерировать слишком большое количество нулевых сообщений.
Допустим, что мы имеем два логических процесса LP. Предположим, что оба они заблокированы. Каждый из них достиг временной отметки, равной 100 (TlocLP1 = 100) и значение n. Пусть следующее запланированное событие имеет временную метку, равную 200. Алгоритм с нулевыми сообщениями будет действовать следующим образом: сообщения будут посланы процессами в моменты времени, равные 101, 102, 103 и т.д. Это будет продолжаться до тех пор, пока процессы не достигнут временной отметки, равной 200. После этого событие с временной меткой 200 (ei, 200), будет выполнено. Т.о., мы видим, что было послано и обработано 100 нулевых сообщений до того момента, когда пришёл черёд ненулевого необработанного события. Из примера рис. 8.6 видно, что алгоритм с нулевыми сообщениями в этом случае неэффективен. Ситуация ещё более изменится к худшему, если мы будем работать с большим количеством процессов.
Рассмотрим пример, который проиллюстрирован на рис. 8.6.
На рисунке видно, что взаимодействуют 3 логических процесса. Нулевые сообщения запланированы на 5.0, 5.5, 6.0 и т.д., они отсылаются через каждые 0.5 минут единиц модельного времени. Нулевых сообщений гораздо больше, нежели в предыдущем примере. Итак, если lookahead мало, то это приводит c к большому количеству нулевых сообщений.
Проблема заключается в том, что мы используем только текущее модельное время и значение предварительного просмотра (lookahead) для вычисления минимальной временной отметки будущих событий процесса. Ключом к усовершенствованию алгоритма является информация о значении временной метки следующего необработанного события. Если бы все логические процессы, участвующие в моделировании, владели этой информацией, они могли бы сразу перевести локальные часы на отметку 200 (TlocLP1 = 200). Таким образом, мы можем избавиться от описанного выше недостатка алгоритма с нулевыми сообщениями.
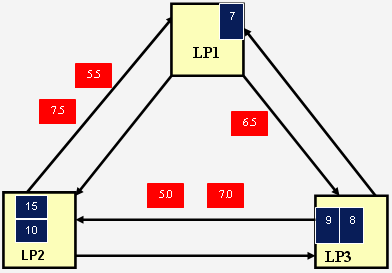
Рис. 8.7. Слишком много нулевых сообщений (lookahead = 0.5)
Многие усовершенствованные алгоритмы используют изложенную только что идею.
Другая проблема заключается в следующем: пусть каждый процесс представляет собой вершину полного графа (каждый процесс может послать сообщение каждому из остальных процессов). При обработке каждого нулевого события каждый процесс выполняет широковещательную рассылку сообщений всем другим процессам. Одним словом, количество генерируемых процессами нулевых событий будет чрезвычайно большим.
Chandy и Misra решили эту проблему следующим образом: вычисления продолжаются до возникновения тупика. Далее тупик обнаруживают и устраняют. Тупик может быть устранён по той причине, что сообщение с минимальным временем безопасно и, следовательно, может быть обработано.
Альтернативой этому решению является вычисление нижней границы с целью увеличить множество безопасных сообщений.
Оптимистическое управление временем
В отличие от консервативных алгоритмов, не допускающих нарушения ограничения локальной каузальности, оптимистические методы не следят за этим ограничением. Однако этот подход гарантирует выявление нарушения каузальности и его устранение. Оптимистический метод имеет два важных преимущества по сравнению с консервативным. Во-первых, ему свойственен более высокий уровень параллелизма. Действительно, если два события могут влиять друг на друга, но алгоритм таков, что на самом деле этого нет, то оптимистический программный механизм позволяет обрабатывать события параллельно в отличие от консервативного. Консервативный метод в этом случае всё равно требует последовательного выполнения этих двух событий. Во-вторых, консервативный механизм обычно требует дополнительной информации, например, расстояние между объектами. Это необходимо для определения безопасного события процесса. Оптимистические алгоритмы, использующие такую информацию, тоже выполняются быстрее, но влияние этой информации на корректность выполнения гораздо меньше. Оптимистический алгоритм, таким образом, более прозрачен при разработке математического программного обеспечения, чем консервативный, разработка программного обеспечения становится проще. С другой стороны, для оптимистического подхода могут потребоваться дополнительные вычисления, что снижает эффективность его применения.
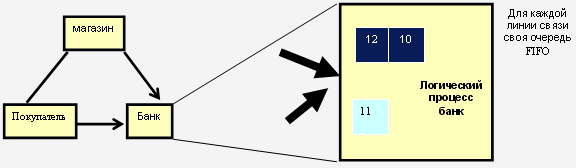
Рис. 8.8. В оптимистическом алгоритме все события, заппанированные на t1=10, t2=11 и t3=12 выполняются
Для оптимистических алгоритмов характерно:
- Логические процессы обмениваются сообщениями с временными метками.
- Топология процессов меняется, т.е. возможно появление новых процессов.
- Сообщения, передаваемые по одной линии связи, не должны быть упорядочены по времени.
- Сеть должна с достаточной надёжностью передавать сообщения, но не отвечает за порядок передачи.
Наиболее известный оптимистический алгоритм – алгоритм, разработанный Джефферсоном. Алгоритм известен под названием Time Warp. Когда логический процесс получает событие, имеющее временную отметку меньшую, чем уже обработанные события, он выполняет откат и обрабатывает эти события повторно в хронологическом порядке. Откатываясь назад, процесс восстанавливает состояние, которое было до обработки событий (используются контрольные точки) и отказывается от сообщений, отправленных "откаченными" событиями. Для отказа от этих сообщений разработан изящный механизм антисообщений.
Антисообщение – это копия ранее отосланного сообщения. Если антисообщение и соответствующее ему сообщение (позитивное) хранятся в одной и той же очереди, то они взаимно уничтожаются. Чтобы изъять сообщение, процесс должен отправить соответствующее антисообщение. Если соответствующее позитивное сообщение уже обработано, то процесс-получатель откатывается назад. При этом могут появиться дополнительные антисообщения. При использовании этой рекурсивной процедуры все ошибочные сообщения будут уничтожены.
Для того чтобы оптимистический алгоритм стал надёжным механизмом синхронизации, необходимо решить 2 проблемы:
- Некоторые действия процесса, например, операции ввода-вывода, нельзя "откатить".
- Обсуждаемый алгоритм требует большого количества памяти (для восстановления состояний процессов в контрольных точках, которые создаются независимо от того, произойдёт откат или нет), требуется особый механизм, чтобы освободить эту память.
Обе эти проблемы решаются с помощью глобального виртуального времени (GVT). GVT –это нижняя граница временной отметки любого будущего отката. GVT вычисляется с учётом откатов, вызванных сообщениями, поступивших "в прошлом". Таким образом, наименьшая временная метка среди необработанных и частично обработанных сообщений и есть GVT. После того, как значение GVT вычислено, фиксируются операции ввода вывода, выполненные в модельное время, превышающее GVT, а память восстанавливается (за исключением одного состояния для каждого из логических процессов).
Вычисление GVT очень похоже на вычисление LBTS в консервативных алгоритмах. Это происходит потому, что откаты вызваны сообщениями или антисообщениями в прошлом логического процесса. Следовательно, GVT – это нижняя граница временной метки будущих сообщений (или антисообщений), которые могут быть получены позже.
Существует несколько алгоритмов для вычисления GVT (LBTS). В асинхронных алгоритмах вычисление GVT выполняется в фоновом режиме во время имитационного прогона. При этом возникает трудность, которая заключается в том, что о локальном минимуме процессы должны извещать в разные моменты времени. Вторая проблема связана с учётом сообщений, которые были отосланы, но ещё не получены. Некоторые авторы (Маттерн(Mattern)) предлагают использовать последовательные отрезки вычислений и счётчики сообщений, эффективно решающие описанные выше проблемы.
Для чистых Time Warp систем характерно чрезмерное "забегание" вперёд некоторых процессов. Это приводит к весьма серьёзной трате памяти и слишком длинным откатам. Большинство оптимистических алгоритмов пытаются ограничить это "забегание". С этой целью вводятся "перемещаемые" в модельном времени окна. Окно определяется как [GVT, GVT+W], где W – это параметр, задаваемый пользователем. Процесс обрабатывает только те события, временные метки которых находятся в данном временном интервале. Существуют более сложные модификации алгоритма синхронизации с перемещаемым окном: для параметра W задаётся алгоритм его пересчёта.
Другой подход заключается в том, что отправка сообщения откладывается до того момента, когда появляется гарантия, что она не состоится позже отката обратно. Другими словами, GVT продвигается до модельного времени, на которое было запланировано событие. Таким образом, исключается необходимость в антисообщениях и исключаются каскадированные откаты (откаты, вызывающие новые дополнительные откаты).
Существует подход, использующий "просмотр назад" (lookback). "Просмотр назад" – это нечто похожее на "предварительный просмотр" в консервативных протоколах синхронизации. Он позволяет избавиться от анти-сообщений.
Кроме того, существует техника прямой отмены, которая иногда используется для срочной отмены некорректных сообщений (Fujimoto).
Другой проблемой, связанной с реализацией оптимистического алгоритма, является большие затраты памяти на хранение исторической информации. Рассмотрим некоторые решения проблемы памяти более подробно:
- Выполнить откат с той целью, чтобы освободить память (Jefferson).
- Выполнять сохранение текущего состояния реже, чем сохранение после каждого события. Периоды сохранения можно указывать в начале моделирования или пересчитывать после каждого сохранённого состояния.
- Выполнять освобождение памяти, занятой векторами состояний, даже в том случае, если их временная метка больше, чем GVT.
Ранние подходы к управлению выполнением Time Warp алгоритма с целью оптимизации основывались на параметрах, задаваемых пользователем. Позже применялись адаптивные подходы, которые следили за выполнением алгоритма и выполняли регулировку этого алгоритма с целью повышения его скорости выполнения.
Выбор алгоритма для реализации системы моделирования
Алгоритмы синхронизации – это достаточно хорошо изученная область дискретного распределённого моделирования. Тем не менее, не существует общего мнения на тот счёт, какой из алгоритмов синхронизации лучше: консервативный или оптимистический. Действительно, выбор алгоритма зависит от конкретного приложения:
- Если приложение имеет хорошие характеристики для использования lookahead (заглядывания вперёд, предварительного просмотра) и вычисление этого lookahead в конечном счёте незначительно увеличивает накладные расходы на разработку приложения, то рекомендуется использовать консервативный алгоритм.
- С другой стороны, в некоторых приложениях оптимистический алгоритм будет выполняться скорее, но к его недостаткам можно отнести тот факт, что реализация оптимистического алгоритма сложна и требует большого количества памяти.
Источник: Синхронизация времени в распределенном имитационном моделировании
А.И. Миков , Е.Б. Замятина. Распределенные системы и алгоритмы.