Источник: Методы Рунге-Кутта
Copyright © 1993, 1994, 1995, 1996, 1997, Nikos Drakos, Computer Based Learning Unit, University of Leeds.

Решение систем обыкновенных дифференциальны уравнений. Методы Рунге-Кутта

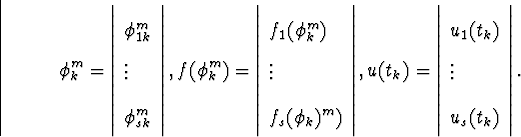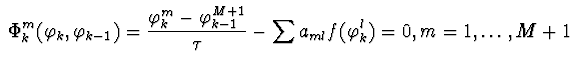
Это одношаговые M -стадийные методы. Введем вектор \begin{displaymath} \phi_k^m=\left\vert\begin{array} {l}\phi_{1k}^m\\ \vdots\\ \... ...{array} {l}u_1(t_k)\\ \vdots\\ u_s(t_k)\end{array}\right\vert .\end{displaymath}и рассмотрим задачу $\frac{du}{dt}=f(u),\enskip u(0)=u_0$.Поставим ей в соответствие разностную задачу (1)\begin{equation} \Phi^m_k(\varphi_k,\varphi_{k-1})=\frac{\varphi^m_k-\varphi^ {M+1}_{k-1}}{\tau}-\sum a_{ml}f(\varphi^l_k)=0,m=1,\ldots,M+1\end{equation}

(8)


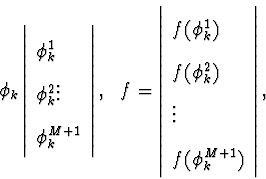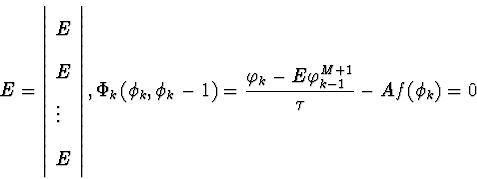
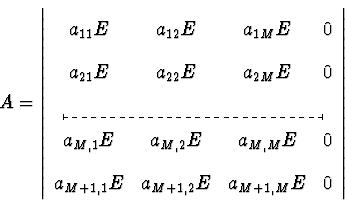где \begin{displaymath} \phi_k\left\vert\begin{array} {l}\phi_k^1\\ \phi_k^2 \vdots... ...f(\phi_k^2)\\ \vdots\\ f(\phi_k^{M+1})\end{array}\right\vert ,\end{displaymath} тогда \begin{displaymath} E=\left\vert\begin{array} {l}E\\ E\\ \vdots\\ E\end{array}\... ..._k-1)=\frac{\varphi_k-E\varphi^ {M+1}_{k-1}}{\tau}-Af(\phi_k)=0\end{displaymath}\begin{displaymath} A=\left\vert\begin{array} {cccc}a_{11}E&a_{12}E&a_{1M}E&0\\ ... ...}E&0\\ a_{M+1,1}E&a_{M+1,2}E&a_{M+1,M}E&0\end{array}\right\vert\end{displaymath}Схема явная, если aml=0 при $\geq m$.Т.е. первые M стадий носят вспомогательный характер, и используются для построения решения на (M+1) стадии.


Лемма 2. Существует $\tau_0\gt$, такое, что при $\tau<\tau_0$ и $\varphi^{M+1}_{k-1}\in B_0:B_{R/2}(z)$ система уравнений (8) имеет единственное решение $\varphi_k\in(B_R(z))^{M+1}$.$\Box$

Мы все время предполагаем, что f обладает постоянной Липшица в BR(z) , и $F(\varphi,\tau,\xi)=E\xi+\tau Af(\varphi)$ удовлетворяет неравенству

\begin{displaymath} \Vert F(\varphi^{(1)},\tau,\xi)-F(\varphi^{(2)},\tau,\xi)\Ve... ...ert\mid A\mid \Vert\cdot\Vert(\varphi^{(1)}-\varphi^{(2)}\Vert.\end{displaymath}Выберем $\tau_0<\frac{1}{L\Vert A\Vert}$.Тогда F сжимающее отображение в шаре BR(z) и уравнение $\varphi_k=F(\varphi_k,\tau,\varphi^{M+1}_{k-1})$ имеет единственное решение в (BR(z)) при $\tau\leq\tau_0$.

$\left\vert \begin{array} {c}0\\ 1\end{array}\right\vert$ -- явная схема Эйлера
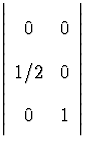$\left\vert \begin{array} {cc} 0 & 0 \\ 1/2 & 0 \\ 0 & 1\end{array}\right\vert$ -- явная для средней точки
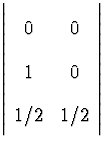$\left\vert \begin{array} {cc} 0 & 0 \\ 1 & 0 \\ 1/2 & 1/2\end{array}\right\vert$ -- явная трапеций
$\left\vert \begin{array} {cccc} 0 & 0 & 0 & 0 \\ 1/2 & 0 & 0 & 0 \\ 0 & 1/2 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 1/6 & 1/3 & 1/3 & 1/6 \end{array}\right\vert$ -- классический Рунге-Кутта метод

Для явных методов M -- стадийный метод можно записать как одностадийный

\begin{displaymath} \Phi_k(\varphi_k,\varphi_{k-1})=\frac{\varphi_k-\varphi_{k-1}} {\tau_k}-\Psi(\tau_k,\varphi_{k-1}).\end{displaymath}

Например для 2 схемы $\Psi(\tau,\varphi_{k-1})=f(\varphi_{k-1}+ \frac{\tau}{2}f(\varphi_{k-1}))$.Нетрудно показать, что $\Psi$ также имеет константу Липшица L0 . И тогда любой метод RK , аппроксимирующий исходную задачу с порядком p , имеет решение сходящееся к точному с порядком p .

Таким образом возникает задача построения схемы с максимальным отношением p/M (явные схемы). До $p=4-p/M=1,\enskip p\gt 5,\enskip P/M<1$.

Метод называется А -устойчивым, если он абсолютно устойчив для линейной задачи $\frac{du}{dt}-Au=0$. Таким является неявный метод. Явных A -устойчивых методов не существует.

L -- устойчивый метод, если собственные числа $(E+\tau A)$ лежат в единичном круге.

Проанализировать устойчивость можно, линеаризуя разностную схему.

Рассмотрим схему \begin{displaymath} \frac{\varphi_k-\varphi_{k-1}}{\tau}-f(\varphi_{k-1}+\frac {\tau}{2}f(\varphi_{k-1}))=0\end{displaymath}\begin{displaymath} \frac{\varepsilon_k-\varepsilon_{k-1}}{\tau}-f^{\prime}_u(\x... ...ac{\tau}{2}f^{\prime}_u(\xi_{k-1})) \varepsilon_{k-1}=0(\tau ')\end{displaymath}\begin{displaymath} \varepsilon_k=\big[E+\tau f^{\prime}_u(\xi+\frac{\tau}{2}f(\... ...{\prime}_u(\xi_{k-1}))\big]\varepsilon_{k-1}+ \frac{\tau^2}{2}C\end{displaymath}

Следовательно требуется контроль на шаге выполнения устойчивости и чаще всего эти требования много жестче, чем условие точности (аппроксимации).

Рассмотрим метод Рунге-Кутта в такой форме

$k_1=\tau f(y)$
$k_2=\tau f(y+a_{21}k_1)$
$k_q=\tau f(y+a_{q1}k_1+\ldots+a_{q,q-1}k_{q-1})$
$y(t_k+\tau)\cong z(t)=y(t_k)+\sum^q_{i=1}p_ik_i$
$\varphi(\tau)=y(t_k+\tau)-z(\tau).$

Пусть $\varphi(0)=\varphi^{\prime}(0)\ldots\varphi^{(s)}(0)=0$

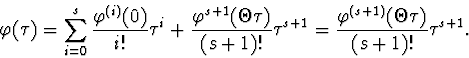
\begin{displaymath} \varphi(\tau)=\sum^s_{i=0}\frac{\varphi^{(i)}(0)}{i!}\tau^i+... ...au^{s+1}=\frac {\varphi^{(s+1)}(\Theta\tau)}{(s+1)!}\tau^{s+1}.\end{displaymath}

Пусть q=2 . Как строится схема?

$\varphi(\tau)=y(t+\tau)-y-p_1\tau f(y)-p_2\tau f(y1)$
$y_1=y+a_{21}\tau f(y)$

Дифференцируем первое уравнение по $\tau$.

$\varphi'(\tau)=y'(t+\tau)-p_1f(y)-p_2f(y_1) -p_2\tau a_{21}f_y(y_1)f(y)$
$\varphi''(\tau)=y''-2p_2a_{21}f_y (y_1)f(y)-p_2\tau a^2_{21}f_{yy}f^2(y)$
$\varphi'''(\tau)=y'''- 3p_2a^2_{21}f_{yy}(\tilde{y})f^2(y)+0(\tau)$
$y'=f,\quad y''=f_yf,\quad y'''=f_{yy}f^2+f_yy''$
$\varphi(0)=0,\quad\varphi'=(1-p_1-p_2)f(y),$
$\varphi''(0)=(1-2p_2a_{21})f_yf, \varphi'''(0)=(1-3p_2a_{21})f_{yy}f^2+ f_yy''$
$\varphi'(0)\Rightarrow 1-2p_1-p_2=0$
$\varphi''(0)=1-2p_2a_{21}=0.$

У нас два уравнения и три неизвестных параметра, задавая один из них мы получим разные схемы.

1)$p_1=0,\quad p_2=1,\quad a_{21}=1/2$

2) $a_{21}=1,\quad p_2=1/2,\quad p_1=1/2$

Так как $\varphi'''(0)\ne 0$, то главный член погрешности -- $\frac{\varphi'''(0)}{6}\tau^3$.Рассмотрим устойчивость, когда f(y)=Ay .

\begin{displaymath} k_1=\tau Ay,\quad k_2=\tau A(y+ta_{21}Ay)\end{displaymath}\begin{displaymath} y(t+\tau)=(E+(p_1+p_2)\tau A+\frac{\tau^2}{2}A^2)y\end{displaymath}\begin{displaymath} T=E+(p_1+p_2)\tau A+\frac{\tau^2}{2}A^2,\quad T_{явл.эйл.}=E+\tau A\end{displaymath}

Пусть $-\lambda_M<\lambda(A)<-\lambda_0$. Тогда схема Эйлера устойчива при $\tau<\frac{2}{\mid\lambda_M\mid}=\tau_0$.Пусть $\frac{\tau}{2}\mid\lambda\mid<1$,\begin{displaymath} -1<1-\tau\mid\lambda\mid(1-\frac{\tau}{2}\mid\lambda\mid)<1,\end{displaymath}и \begin{displaymath} 2-\tau\mid\lambda\mid(1-\frac{\tau}{2}\mid\lambda\mid)\gt,\end{displaymath}то есть наша схема устойчива при $\tau<\tau_0(1-\frac{\tau}{2}\mid \lambda\mid)$.


Источник: Методы Рунге-Кутта
Copyright © 1993, 1994, 1995, 1996, 1997, Nikos Drakos, Computer Based Learning Unit, University of Leeds.