Фельдман Л.П. Общие линейные блочные многошаговые методы

Автор: Л.П. Фельдман, д-р техн. наук

Донецкий национальный технический университет

Украина, 83001, Донецк, ул. Артема, 66.

тел. (062)3010856, e-mail: feldman@r5.dgtu.donetsk.ua

Общие линейные блочные многошаговые методы решения задачи Коши для обыкновенных дифференциальных уравнений

Abstract

Рассмотрены обобщенные блочные многошаговые многоточечные методы решения задачи Коши для системы обыкновенных дифференциальных уравнений. Получены расчетные формулы для общих m- шаговых k- точечных блочных методов, определен порядок их точности. Определены условия устойчивости по Далквисту и доказана сходимость устойчивых по начальным данным общих m-шаговых k-точечных блочных методов к точному решению. Получена априорная оценка погрешности приближенного решения. Приведен пример решения задачи Коши двухшаговым двухточечным блочным методом. Полученные результаты представляют возможности построения новых более эффективных параллельных алгоритмов и их реализации на современных мультипроцессорных вычислительных системах.

Введение

Статья содержит обобщение результатов исследований [1-6], посвященных параллельным методам численного решения задачи Коши для систем обыкновенных дифференциальных уравнений и является продолжением работ [7-13]. В ней рассматривается устойчивость решения по начальным данным, получена оценка точности решения, приводится доказательство сходимости приближенного решения для общих m-шаговых k-точечных блочных методов, что представляет обобщение ранее опубликованных результатов. Приведен пример решения блочным разностным методом и даны практические рекомендации их использования для более широкого набора параллельных разностных схем.

1. Погрешность аппроксимации блочных методов

Пусть для численного решения задачи Коши

(1)

используется блочный m-шаговый k-точечный разностный метод вида:

(2)

Коэффициенты уравнений (2) определены с точностью до множителя. Чтобы устранить этот произвол, будем считать, что выполнено условие:

(3)

Выражения для невязок на решении x(t) исходного дифференциального уравнения имеют вид:

(4)

где .

Для i-го уравнения (2) потребуем его аппроксимации в токе

Разлагая и в ряды Тейлора в окрестности точки t_{n, 0}, получим:

Подставляя эти разложения в выражение (4), будем иметь:

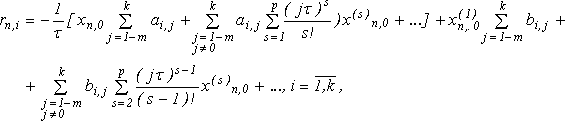
Сгруппируем члены с одинаковыми степенями , тогда получим

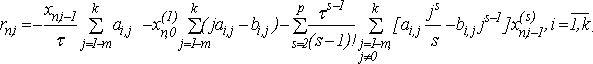(5)

Отсюда следует, что погрешность аппроксимации имеет порядок p, если выполнены условия

(6)

Каждое уравнение системы (6), (3), соответствующее фиксированному значению i, может содержать 2(k+m) неизвестных a_{i, j}, b_i,j. Для того, чтобы система разностных уравнений, построенных на одном наборе узлов сетки, была линейно независима, шаблоны разностных схем для уравнений должны отличаться между собой хотя бы одним вхождением либо коэффициента a_{i, j}, либо b_{i, j}. Отсюда следует, что наивысший порядок аппроксимации m-шагового k-точечного блочного метода не может превосходить p = 2(k + m)-3. Его погрешность в соответствии с (5) определяется формулой:

(7)

Упростим второе уравнение (6), учитывая (3):

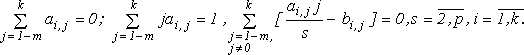(8)

Приведем пример двухшаговой двухточечной разностной схемы наивысшего (пятого) порядка точности, полученной по формулам (8):

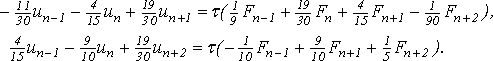
2. Общая процедура интегрирования

Обозначим матрицы коэффициентов системы уравнений (2) через

Разобьем каждую из матриц на две части:

,
.

Введем соответствующие им вектора

В векторной форме уравнение (2) будет иметь вид

Предполагая, что матрица невырожденная, разрешим последнее уравнение относительно

, (9)

где .

Предположим, что решение разностной задачи сходится к решению исходной задачи. Заметим, что условия сходимости приближенного решения рассматриваются ниже. Вычислим стартовые значения, например, с помощью явных формул Рунге – Кутта

Затем на каждом последующем этапе необходимо решить нелинейное уравнение (9), определив последовательно вектора V₁, V₂,..., для соответствующих значений векторов U₀, U₁, U₂,...

3. Устойчивость по начальным данным

Задача Коши для однородного уравнения, соответствующего (9) состоит в отыскании сеточной функции , удовлетворяющей при всех n ≥ 0 уравнению:

V_n+1 = SU_n (10)

при и принимающей при n = 0 заданные начальные значения .

Обозначим элементы матрицы . Для доказательства устойчивости преобразуем уравнения (10) к эквивалентной системе. Пусть , тогда эта система будет иметь вид:

u_n,-m+k+1 = u_n,-m+k+1,..., u_n,0 = u_n,0,

u_n+1 = s_1,1u_n-m+k+1 + s_1,2u_n-m+k+2 + ... + s_1,mu_n, (11)

u_n+k = s_k,1u_n-m+k+1 + s_k,2u_n-m+k+2 + ... + s_k,mu_n.

Представим ее в векторной форме:

, (12)
W_n = {u_n,1-m, u_n,2-m, ..., u_n,0} W_n+1 = {u_n,k-m+1, u_n,k-m+2, ..., u_n,k}

W₀ = U₀ = {u_0,1, u_0,2,..., u_0,n}, где

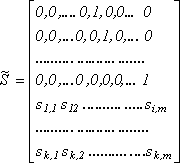(13)

В матрице (13), размерности m × m, последние k строк совпадают с матрицей S, а первые m-k соответствуют первой строке уравнений в (11).

Для случая m ≤ k, в векторной записи (12) следует положить

W_n = {u_n,1-k, u_n,2-k, ..., u_n,0} W_n+1 = {u_n,1, u_n,, ..., u_n,k} (14)

W₀ = U₀ = {0, ..., 0, u_0,1, u_0,2,..., u_0,n},

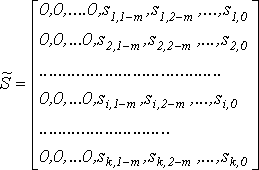. (15)

В матрице (14), размерности k × k, элементы первых m столбцов равны нулю, а последние m-k совпадают с матрицей S.

Оказывается что, также как и в случае многошаговых разностных методов, рассмотренных в [1,3,4,5], устойчивость или неустойчивость уравнения (12) по начальным данным определяется расположением корней характеристического уравнения матрицы Будем считать, что условие корней выполнено для матрицы , если все корни ее характеристического уравнения лежат внутри или на границе единичного круга, причем на границе круга нет кратных корней.

Используем следующее определение устойчивости блочных многошаговых разностных методов[3].

Уравнение (12)устойчиво по начальным данным,если существует постоянная M не зависящая от n и такая, что при любых начальных данных для его решения выполняется оценка

(16)

Тем самым устойчивость означает равномерную по n ограниченность решения задачи Коши. Это определение равносильно требованию равномерной ограниченности матрицы при всех n ≥ 0 [4]. В самом деле (12) можно записать в виде:

Для доказательства условий устойчивости по начальным данным уравнения (12) используются следующие утверждения:

Лемма 1. Для любого существует норма вектора такая, что для подчиненной нормы матрицы справедливо неравенство

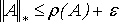Лемма 2.Если все корни характеристического уравнения матрицы лежат внутри или на границе единичного круга комплексной плоскости, причем на границе круга нет кратных корней, то существует норма вектора такая, что для подчиненной нормы матрицы справедливо неравенство [3].

Следующая ниже теорема 1 является обобщением на блочные методы аналогичного утверждения для многошаговых разностных методов

Теорема 1. Условие корней необходимо и достаточно для устойчивости уравнения (12) по начальным данным.

Доказательство необходимости. Пусть матрица имеет собственное число q_k > 0. Тогда для любой подчиненной нормы матрицы , следовательно, оценка (16) в этом случае невыполнима.

С помощью преобразования приведем матрицу к модифицированной жордановой форме и введем норму вектора.

. (17)

Пусть среди собственных чисел матрицы лежащих на границе единичного круга есть кратные, т.е. кратности r. Тогда, соответствующая этому собственному числу клетка матрицы имеет вид:

Для нормы матрицы получим оценку:

Оценка (16) в этом случае также невыполнима.

Доказательство достаточности. Из уравнений (12),

следовательно

(18)

По определению нормы

С другой стороны, для любой невырожденной матрицы Q справедливо тождество

Из которого следует оценка

Таким образом, если норма определена равенством (17), то выполняются оценки

(19)

Из (18) и (19) следует

и получим оценку

которая показывает, что существует постоянная не зависящая от n, т.е. условие устойчивости по начальным данным (16) выполняется.

1.Заметим, что одношаговые m = 1 и многошаговые m > 1, k=1,2,… блочные методы, определяемые формулой

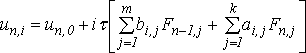рассмотренные в статьях [8-12] всегда устойчивы по начальным данным.

2. Проверим устойчивость по начальным данным разностного блочного двухшагового двухточечного метода пятого порядка аппроксимации (см. п. 1). Соответствующие матрицы приведены ниже

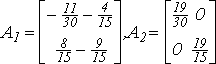
Перейдем к эквивалентной системе разностных уравнений (11). Введем вектора

Представим эту систему в векторной форме (12): .

В рассматриваемом примере матрицы совпадают. Проверим устойчивость по начальным данным, для чего найдем матрицу:

Корни ее характеристического уравнения одинаковы и равны 1. Проверим их кратность. Для этого приведем матрицу к нормальной Жордановой форме, которая имеет вид .

Жорданова матрица представляет собой клетку для кратного корня q₁ = q₂ = 1. Поэтому рассмотренный разностный блочный двухшаговый двухточечный метод неустойчив по начальным данным.

Для сравнения приведем матрицы коэффициентов уравнений разностного блочного двухшагового двухточечного метода четвертого порядка аппроксимации:

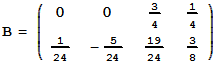. (20)

Матрица перехода для соответствующей системы однородных уравнений имеет вид:

Нормальная жорданова форма этой матрицы равна:

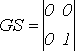Корни характеристического уравнения матрицы S равны q₁ = 0, q₂ = 1. Поэтому рассмотренный разностный блочный двухшаговый двухточечный метод четвертого порядка точности устойчив по начальным данным.

Оказывается, что методы наивысшего порядка аппроксимации, как показывает следующая теорема, практически не пригодны для расчетов [3,4].

Теорема 2. Первый барьер Далквиста. Порядок p–устойчивого m-шагового k- точечного блочного метода подчиняется следующим ограничениям p ≤ m+k при m+k четных и p ≤ m+k-1 при m+k нечетных [4].

3. Рассмотрим устойчивость по начальным данным разностного блочного трехшагового трехточечного метода Биккарта, формулы которого приведены ниже. Первое и второе уравнение получим по двухшаговой формуле Гира [3]:

Первое и второе уравнение имеют точность третьего порядка. Коэффициенты третьего уравнения получим как решение уравнений (8):

Это уравнение четвертого порядка точности. Приведем матрицы коэффициентов однородных разностных уравнений:

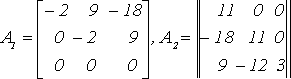Найдем матрицу перехода:

Приведем матрицу к нормальной жордановой форме:

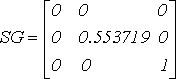Собственные числа матрицы различны и равны q₁ = 0, q₂ = 0.553719, q₃ = 1. Поэтому рассмотренный метод устойчив по начальным данным.

4. Устойчивость по правой части

В предыдущем пункте была получена оценка решения однородного уравнения (12) через начальные данные. Получим здесь оценку решения неоднородного уравнения:

. (9)

Аналогично п.3. перейдем к эквивалентной системе уравнений:

…, ,

………………………………………

(22)

Введем вектора

(23)

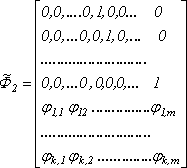Использовав введенные вектора, получим вместо (9) следующее уравнение:

. (24)

Значения заданы. Для каждой правой части решение задачи Коши может быть найдено по формуле (24). Представим уравнение (24) в виде :

(25)

H_n = {h_n,-m+1, h_n,-m+1, ..., h_n,0}, Y_n = {y_n,1-m, y_n,2-m, ..., y_n,0}.

Матрица определена согласно (13).

Пусть уравнение (12) устойчиво по начальным данным. Тогда согласно теореме 9.1 выполнено условие корней, т.е. для некоторой нормы матрицы справедливо неравенство . Таким образом, из (25) получаем неравенство:

Суммируя эти неравенства по n от 1 до l, получим:

. (26)

Используя далее неравенство (19), устанавливающее эквивалентность норм и . Тогда, из (26) получим:

(27)

Отсюда, получим

Таким образом,

, (28)

где .

Выполнение оценки (28) означает по определению устойчивость уравнения (25) по правой части [3].

5. Оценка погрешности разностного метода

Обозначив вектор погрешности решения разностного уравнения (24) через

где

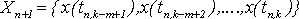Подставив 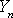в уравнение (24) получим

(29)

Добавим к правой части уравнения (29) и вычтем из нее выражение

где

Тогда, уравнение для погрешности будет иметь вид:

(30)

где через обозначен вектор погрешностей аппроксимации разностных уравнений:

. (31)

Погрешность аппроксимации оценивалась выше формула (7), где были найдены условия p-го порядка аппроксимации. В частности, при выполнении этих условий при . Через обозначена функция:

. (32)

(33)

(34)

Предположим, как и ранее, что f(t,x) удовлетворяет условию Липшица по второму аргументу, т.е.

. (35)

Тогда, для функции выполнена оценка

где .

Откуда получим

Подставляя эту оценку в (30), получим:

Выразим отсюда норму вектора погрешности для n+1 блока

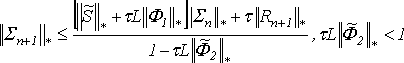(36)

Учитывая устойчивость разностных уравнений по начальным данным, перепишем неравенство (36) в виде:

Из последнего неравенства, учитывая (19) получим

или короче

. (37)

Далее, учитывая (19), имеем

Подставляя эти неравенства в (37), получим:

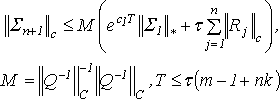(38)

Следствие. Если , выполнено условие корней, при и разностное уравнение (2) аппроксимирует исходное уравнение (1), то решение разностной задачи (2) сходится при к решению исходной задачи (1).

Доказательство следует из того, что при первое слагаемое правой части (38) в силу условия следствия, а в силу аппроксимации с порядком p > 1.

Пример. Решим двухшаговым двухточечным методом четвертого порядка аппроксимации (20) следующую задачу Коши:

x' = -10(t-1)x, x(0) = 1. (41)

Точное решение задачи известно и имеет вид:

x(t) = Exp[-5t(t-2)]

Используем в программе это обстоятельство для нахождения дополнительного значения в первой точке разностной сетки, т.е. при . Введем точное решение x(t), правую часть дифференциального уравнения f(t,x), производную .

В левой части уравнений оставим неизвестный вектор V_n+1 , остальные члены перенесем в правую часть уравнений.

Введем матрицы A и B:

разобьем матрицы A и B:

Разрешим уравнение относительно неизвестного вектора

Итерационный процесс получения решения на очередном шаге организуем по алгоритму:

Введем матрицу BS :

определим процедуру -функцию правой части уравнения и для оценки погрешности известное точное решение рассматриваемой задачи Коши. Введем исходные данные:

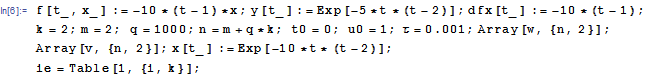
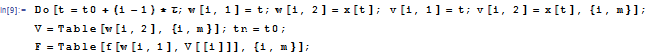
и выполним расчеты :

Приведем графики приближенного решения и глобальной погрешности полученного решения.

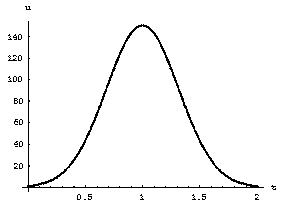
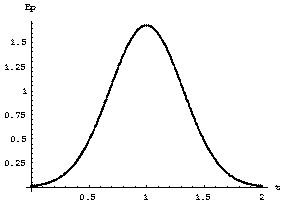
а б

Рис.1. Графики решения – а и глобальной погрешности решения - б задачи Коши (41) двух шаговым двух точечным методом четвертого порядка точности

Заключение

Общие блочные многошаговые многоточечные методы, рассмотренные в статье, представляют обобщение известных многошаговых методов и существенно расширяют класс разностных методов решения задач Коши для обыкновенных дифференциальных уравнений. Проведенный анализ этих методов позволил получить оценки их устойчивости по Далквисту, сходимости по правой части и оценки погрешности. Полученные результаты представляют возможности построения новых более эффективных параллельных алгоритмов и их реализации на современных мультипроцессорных вычислительных системах.

Литература

Дж. Холл, Дж. Уатт. Современные численные методы решения обыкновенных дифференциальных уравнений. - М.: Мир, 1979. –312с.
Системы параллельной обработки. Под ред. Ивенса Д. М.: Мир,1985. – 416с.
Самарский А.А., Гулин А.В. Численные методы.- М.: Наука, 1989.- 432с.
Хайрер Э., Нёрсет С., Ваннер. Г. Решение обыкновенных дифференциальных уравнений. Нежесткие задачи. - М.: - Мир, 1990.-512с.
Хайрер Э., Ваннер. Г. Решение обыкновенных дифференциальных уравнений. Жесткие задачи. - М.: Мир, 1999.- 685с.
Молчанов И.Н. Введение в алгоритмы параллельных вычислений. АН УССР, Инст. Кибернетики им. В.М. Глушкова. Киев: Наукова думка. 1990. -128с.
Фельдман Л.П. Параллельные интерполяционные алгоритмы численного решения задачи Коши для обыкновенных дифференциальных уравнений на SIMD компьютере. Научн. Тр. ДонГТУ. Серия: Проблемы моделирования и автоматизации проектирования динамических систем, выпуск 10:- Донецк: ДонГТУ, 1999, с. 20-25.
Фельдман Л.П. Сходимость и оценка погрешности параллельных одношаговых блочных методов моделирования динамических систем с сосредоточенными параметрами. Научн. Тр. ДонГТУ. Серия: Iнформатика, Кiбернетика та обчислювальна технiка, выпуск 15:- Донецк: -ДонГТУ,2000, с. 34-39.
Feldmann L.P. Implementierung und Effizienzanalyse von parallelen blockartigen Simulati onsalgorithmen für dynamische Systeme mit konzentrierten Parametern. In: Möller, D.P.F. (Hrsg.): Tagungsband 14. ASIM-Symposium Simulationstechnik in Hamburg, September 2000, SCS-Europe BVBA, Ghent/Belgium 2000, S. 241-246.
Фельдман Л.П., Дмитриева О.А. Разработка и обоснование параллельных блочных методов решения обыкновенных дифференциальных уравнений на SIMD–структурах. Научн. Тр. ДонГТУ. Серия: Проблемы моделирования и автоматизации проектирования динамических систем, выпуск 29:- Донецк: ДонГТУ, 2001, с. 70-79.
Feldman L.P., Dmitrieva O.A., Gerber S.. Abbildung der blockartigen Algorithmen auf Parallelrechnerarchitekture. In: Tavangarian,D., Grützner,R. (Hrsg.): Tagungs-band 15. ASIM-Symposium Simulationstechnik in Rostock, September 2002, SCS-Europe BVBA, Ghent/Belgium 2002, S.359-364.
Фельдман Л.П. Параллельные алгоритмы моделирования динамических систем, описываемых обыкновенными дифференциальными уравнениями. //Электронное моделирование, том 26, № 1, 2004.- С. 19-30.
Фельдман Л.П., Назарова И.А. Параллельные алгоритмы численного решения задачи Коши для систем обыкновенных дифференциальных уравнений. //Математическое моделирование, том 18, №6, 2006. - С. 17-31.