Завалкин Д.А. Параллельные одношаговые блочные методы решения задачи Коши

Автор: Д.А. Завалкин, магистрант

Донецкий национальный технический университет

e-mail: dimzav@gmail.com [dimzav at gmail dot com]

Тезисы к докладу на конференции "Компьютерный мониторинг и информационые технологии 2008" на тему "Параллельные одношаговые блочные методы решения задачи Коши"

В теории численных методов, и решения дифференциальных уравнений в частности, многие алгоритмы, успешно используемые в последовательных вычислениях, оказываются не применимыми при проведении параллельных вычислений. Отсюда вытекает необходимость построения специальных методов, адаптированных к вычислительным системам с параллельной архитектурой.

При этом следует учитывать, что метод должен обладать численной устойчивостью и иметь оптимальную для сохранения эффективности структуру. Данным требованиям удовлетворяют блочные методы [1].

В блочных методах для блока из k точек новые k значений функции вычисляются одновременно, что вполне согласуется с архитектурой параллельных вычислительных систем. Такой принцип позволяет вычислять коэффициенты разностных формул не в процессе интегрирования, а на этапе разработки метода, что значительно увеличивает эффективность счета. В то же время для блочных методов отсутствуют оценки погрешностей и условия сходимости.

Рассмотрим решение задачи Коши

f(t,x), x(t₀) = x₀ (1)

k точечным блочным разностным методом. Множество M точек равномерной сетки t_m, m=1,2,…,M и t_M=T с шагом разобьем на N блоков, содержащих по k точек, при этом kN ≥ M. В каждом блоке введем номер точки i =0,1,…,k и обозначим через t_n_,_i точку n –го блока с номером i. Точку t_n_,0 назовем началом блока n, а t_n_,_k – концом блока. Очевидно, что имеет место t_n_,_k₌ t_n_+1,0. Условимся начальную точку в блок не включать [2].

Рисунок 1 – Схема разбиения на блоки множества M точек равномерной сетки t_m

Если для расчета значений в новом блоке используется только последняя точка предшествующего – блочный метод считается одношаговым, а если все точки предшествующего блока – многошаговым.

Рисунок 2 – Шаблон разностной схемы одношагового блочного метода

В общем случае уравнения одношаговых разностных методов для блока из k точек с учетом введенных обозначений можно записать в виде

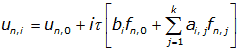(2)

– номер точки

– номер шага

Для решения полученной нелинейной системы уравнений можно использовать:

- итерационный метод;

- метод Ньютона.

Для того, чтобы сделать вывод о целесообразности реализации и выгоды, получаемой при применении параллельного метода необходимо знать его ускорение и коэффициент параллелизма.

Введем обозначения:

t_f – время вычисления значения функции f(t,x);

t_сл – время выполнения операции сложения;

t_ум – время выполнения операции умножения;

t_об – время передачи числа соседнему процессору.

Время вычисления на одном процессоре с точностью O(τ^k+1) во всех k узлах блока по формулам Рунге-Кутта k+1 порядка точности равно

(3)

Время параллельного вычисления на k процессорах приближенных значений решения во всех k узлах sблока равно

(4)

Тогда ускорение параллельного одношагового k-точечного алгоритма равно

(5)

Коэффициент эффективности параллельного алгоритма вычисляется по формуле

(6)

Здесь N_проц – количество используемых процессорных элементов. В нашем случае

(7)

Поэтому

(8)

Литература

Системы параллельной обработки: Пер. с англ./ Под. ред. Ивенса Д.- М.: Мир,1985-416с.
Фельдман Л.П. Сходимость и оценка погрешности параллельных одношаговых блочных методов моделирования динамических систем с сосредоточенными параметрами // Научные труды ДонНТУ. Серия: Информатика, моделирование и вычислительные методы, (ИКВТ-2000), выпуск 15: Донецк: ДонНТУ, 2000, с. 34-39.