Как мы видим, различие систем координат СК-95г и WGS-84, UTM состоит в несколько разных размерах большой полуоси исходных эллипсоидов и в довольно существенной разнице масштабов по осевому меридиану. Поскольку системы координат используют одну проекцию, то для съемочных сетей, формулы вычисления поправок за редукцию измеренных величин будут общими. Мы не будем приводить всех поправок, которые крайне малы и вводятся только при обработке высокоточных геодезических сетей. Рассмотрим только редукцию измеренных линий на эллипсоид и на плоскость.

Формулы вычисления редукций.

Редуцирование измеренных линий на поверхность референц- эллипсоида.

Можно записать:

Dэ=D*(1-H/R) (2)

где:   D    -   горизонтальное проложение измеренной линии на местности;

Dэ   -   значение линии, приведенной на референц-эллипсоид;

H     -   средняя высота линии над референц-эллипсоидом;

R     -   средний радиус кривизны эллипсоида в средней точке линии;

Для территории России принимаем среднее значение  R=6380000 м  [1]

Редуцирование линий на плоскость

Поскольку стороны в съемочном обосновании редко превышают 1000 м, то формулу 1 [1] можно записать в следующем виде:

Dп=Dэ*mo*(1+YmІ/2RІ)   (2)

где   Dп   -  значение линии редуцированной на плоскость;

Ym   -  среднее значение ординаты (Расстояние от осевого меридиана) линии в проекции  (Y1+Y2)/2;

mo   -  значение масштабного коэффициента по осевому меридиану;

На основании формул 1 и 2 получаем формулу суммарной поправки в линии:

D=D*(1-H/R)*mo*(1+YmІ/2RІ) (3)

В СК-95г и WGS-84, UTM для исключения отрицательных значений, ордината имеет смещение на +500000м. Формула (3) будет иметь вид:

D=D*(1-H/R)*mo*(1+(Y-500000)І/2RІ) (4)

где: Y   -  значение ординаты из каталога;

Используя формулу ( 4 ) вычислим поправки за редукцию на эллипсоид и за редукцию на плоскость в системах координат СК-95г и WGS-84, UTM в линии длиной 1000 метров.

Как видно из таблиц, поправки могут быть как совсем небольшими, так и достигать значительных величин.

Возникает вопрос: «Всегда ли надо вводить поправки?»

Среднеквадратическая погрешность линейных измерений при создании планового обоснования должна быть не менее 1/4000. Это среднеквадратическая ошибка 0.250м на один километр. Пренебрегаемо малыми можно считать ошибки, не превышающие 10 – 20% от среднеквадратической. Возьмем величину в 20% - получим 0.050м на километр.

В таблицах 2 и 3 желтым цветом выделены поправки менее 0.050 м на один километр. То есть, когда поправки можно не учитывать. Жирным курсивом выделены ошибки более среднеквадратической (более 0.25м на 1000м), когда поправки однозначно необходимо вводить в измеренные линии.

Система координат 95года.  Ширина зоны в СК-95г равна 6 градусам. На территории России максимальное расстояние от осевого меридиана до края зоны составляет порядка 250 км. На краю зоны поправки за редуцирование могут достигать 0.76м на 1000м. Однако стоит отметить, что в диапазоне: высот от 0 до 500м и на расстоянии от осевого меридиана от 0 до 50км, редукции весьма малы. На каждом отдельном объекте геодезистам необходимо оценивать поправки за редукции и самостоятельно принимать решение о целесообразности их введения в измеренные линии.

Система координат 63г.  Ширина зоны в СК-63г равна 3 градусам. Максимальное расстояние до края зоны в России составляет порядка 125 км. Обратимся к таблице 2. Учитывая, что в подавляющем большинстве случаев расстояние от осевого меридиана редко достигает 100км, можно сделать вывод о том, что в большинстве случаев поправки за редукцию измеренных линий будут небольшими. В том случае, если все необходимые параметры известны, то можно рассчитать и оценить величину поправки за редукцию.

Система координат  WGS-84, UTM.  Поправки значительные. Небольшие по своей величине поправки только при расстоянии 200км от осевого меридиана. При работе с системой координат WGS-84, UTM поправки за редуцирование линий необходимо вводить постоянно.

Уравнивание геодезических сетей по способу наименьших квадратов (МНК) производится при условии, что:

• все измеренные в сети величины являются независимыми

• в результатах измерений отсутствуют систематические ошибки

• случайные ошибки измерений подчиняются закону нормального распределения

Погрешности, вызванные игнорированием редукций, аналогичны систематическим ошибкам. Корректное уравнивание сетей съемочного обоснования вследствии этого невозможно.

Тем не менее, считается, что поправки при уравнивании компенсируют поправки за редукции. Поэтому при создании планового обоснования нет необходимости в учете этих редукций.  Рассмотрим этот вопрос на примере двух теодолитных ходов.

Уравнивание теодолитных ходов.

Воспользуемся программой CREDO DAT. Создадим проект теодолитного хода с нулевой невязкой, с учетом параметров СК-42г. Координаты возьмем в проекции Гаусса-Крюгера, ордината – 150 км, отметка 50м над уровнем моря. Суммарная поправка 0.269м на 1000 метров. Получим таким образом «истинные» координаты. После этого установим систему координат «Местная» и отключим учет поправок. Смоделируем уравнивание хода без ошибок в измерениях, но и без редукций. Сравним полученные результаты.

Пример первый.

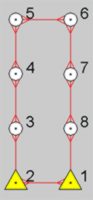
Ход в виде буквы П.  Схема хода на рис.1.  Журнал измерений на рис.2.

Рис. 1	Рис. 2

Линейная невязка, в характеристиках хода (табл.5), составляет всего 8 см. Однако погрешности по линии 2-6 и по линии 7-1 компенсируют друг друга и на конечную плановую невязку хода не влияют. Полные погрешности вычисления координат точек в слабом месте хода ( точки 5 и 6 ) составляют 0,245м.  Много это или мало? Длина хода 2100м. Согласно СП 11-104-97 ход такой протяженности может служить плановым обоснованием для топографической съемки масштаба 1:1000 ( табл. 5.1, прим.1 [3] ).

Допустимая средняя ошибка определения координат точек хода составляет 0.1 мм в масштабе плана. В нашем случае – 0.10  м. Соответственно средняя квадратическая ошибка – 0.14 м и предельная ошибка – 0.28 м.

Полученная погрешность определения координат точек теодолитного хода в слабом месте практически равна предельной погрешности.

Пример второй.

Ход с координатной привязкой. Схема хода на рис. 3.  Журнал измерений на рис. 4.

рис. 3. Схема хода	Рис. 4.  Журнал измерений хода

В данном примере полные погрешности вычисления координат точек в слабом месте хода (точки 6 и 7) составляют 0.204 м. Длина хода 2250 м. Согласно СП 11-104-97, ход такой протяженности может служить плановым обоснованием для топографической съемки масштаба 1:1000 (табл.5.1, прим.1 [3]). Допустимая ошибка определения координат точек хода составляет 0.1 мм в масштабе плана. В нашем случае – 0.1 м. Соответственно средняя квадратическая ошибка – 0.14 м и предельная ошибка – 0.28 м.

Полученная погрешность составляет 70% от предельной погрешности.

Вследствии того, что ход с координатной привязкой, искажаются не только линии, но и азимуты сторон. В таблице 7 приведены дирекционные углы сторон хода. Искажения достигают 02'34". Так же показателен тот факт, что вычисленная фактическая угловая ошибка хода ( табл. 8 ) превышает допустимую погрешность.

В обоих примерах полученные погрешности определения координат точек планового обоснования, в слабом месте, сопоставимы с предельно допустимыми ошибками. В примере хода с координатной привязкой, ошибки дирекционного угла стороны достигли 02'34". Все эти ошибки обусловлены только неправильной математической обработкой. Если добавить ошибки измерений, то погрешности будут гораздо больше. Возможно, из-за этого появляется недоверие к уравниванию геодезических сетей в целом.

Рекомендации по обработке геодезических измерений.

1. При помощи программы CREDODAT.

Создание различных систем координат в проекте CREDO DAT 3.0 детально описано в главе 3 описаний к программе и в статье «Создание пользовательской системы координат в CREDO_DAT»  [ 1 ]. Параметры проекций Гаусса-Крюгера и UTM приведены в таблице 1  данной статьи. Однако необходимо добавить, что для правильного редуцирования измеренных линий на эллипсоид, необходимо вводить отметки точек. При совместной обработке нивелирования и плановых сетей проблем не возникает. Если же уравнивается только плановое обоснование, то можно вводить отметки для каждой точки. Либо можно ввести среднюю отметку на объекте.  При правильной настройке проекта все поправки вносятся в измеренные величины автоматически.

2. При помощи программы «TRIMBLE GEOMATIC OFFICE» (далее TGO).

В TGO необходимо установить систему координат. Можно воспользоваться готовой или создать свою. Так же, после установления системы координат, поправки определяются автоматически. В программе TGO при решении обратной задачи рассчитывается длина линии в проекции (Crid Distance), на эллипсоиде (Ellipsoid Distance), на Земной поверхности (Ground Distance). См. рис 5. Это весьма удобно. Можно сразу оценить разницу между расстоянием измеренным на местности (Ground Distance) и расстоянием в проекции (Crid Distance). В примере на рис.5, расстояние на местности равно 1070.241м , а расстояние в проекции равно 1069.972м. Разница составляет 0.269м на 1070 метров.

Рис. 5

3. Ввод поправок в измерения за редукции «вручную» при помощи таблиц.

Можно составить таблицы поправок для конкретного объекта, рассчитав поправки по формуле ( 3 ). Выбрать интервал значений Y (от 50км до 65 например) и среднюю отметку для объекта. По одной оси откладывать Y, по другой длины линий.  Интервал линий рекомендуется брать через 10метров (210м, 220м, 230м и т.д.). Интервал значений Y через 10 км.

Выводы и рекомендации.

Список использованной литературы: