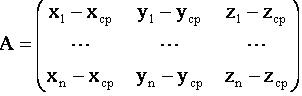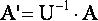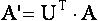|
Врачева Анна Александровна
Факультет:
Горно-геологический
e-mail: anna.vracheva@gmail.com
|
||||||||||||||||
| Главная страница ДонНТУ Портал магистров ДонНТУ Кафедра геоинформатики и геодезии | |||||||||||||||||
|
Автореферат магистерской работы Тема: «Анализ методов и геодезических технологий
наземного лазерного сканирования» |
|||||||||||||||||
|
RUS |
|||||||||||||||||
|
Введение
Рисунок 1 – Принцип работы лазерного сканера
Для определения расстояний существуют два метода. Первый метод носит название Time-of-Flight (TOF). Он основан на измерении времени действия лазерного импульса. Этот импульс производится сенсором, отражается объектом и принимается чувствительным элементом.
n – коэффициент преломления среды; 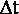 - время действия импульса. - время действия импульса. Второй метод основан на измерении разности фаз. Сенсор излучает гармонические колебания известной длины волны, в этот момент определяется начальная фаза, затем сигнал отражается объектом и принимается чувствительным элементом, в этот момент определяется конечная фаза. Расстояние определяется по формуле:
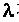 – длина волны; – длина волны;  – конечная и начальная фаза измерений соответственно. – конечная и начальная фаза измерений соответственно. По углу разворота зеркал в момент наблюдения и измеренному расстояние, процессор вычисляет координаты каждой точки по формуле:
D – измеренное расстояние; 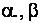 – горизонтальный и вертикальный углы соответственно. – горизонтальный и вертикальный углы соответственно.Актуальность и цель
В большинстве случаев в результате лазерного сканирования информация об объектах представляется в виде прямоугольных декартовых координат, совокупность которых образует, так называемое «облако» точек. Обзор исследований и разработок по теме
Существуют различные алгоритмы определения плоскостей. В частности Andreas Rietdorf в своей работе «Automatisierte Auswertung und Kalibrierung von scannenden Messsystemen mit tachzmetrischem Messprinzip» (Munhen 2005) [1] в качестве критерия для решения, лежат ли точки на плоскости, выполнял расчет определителя. Исследуются соответственно два смежных треугольника, которые достаточно точно определяют плоскость.
Рассмотрим другой алгоритм.
Рассмотрим преобразование координат точек составляющих матрицу Х. Геометрически это можно изобразить следующим образом: рис. 2.
Рисунок 2 – Преобразование координат точек плоскости, здесь: система координат
Вычтем из каждой координаты матрицы Х средние значения (
Умножим матрицу А на АТ получим симметричную матрицу N. Это необходимо для нахождения собственных векторов (U) матрицы А.
где A’ – преобразованная матрица координат точек; А – исходная матрица; U – матрица преобразования координат при переходе к новому базису. Если собственные числа матрицы А попарно различны, то собственные вектора являются ортогональными и линейно независимыми, а, следовательно, их можно использовать в качестве базиса. Тогда формула (6) имеет следующий вид:
А – исходная матрица; U – матрица преобразования координат при переходе к новому базису, состоящая из собственных векторов матрицы А. Планируемые результаты
Результатом работы будет создание программы в среде Delphi, позволяющей выделять геометрические примитивы. Окончательные выводы по результатам исследования планируется сделать к декабрю 2008г. В данный момент можно сказать, только что описанный алгоритм с использованием анализа преобразованных координат дает большую надежность полученных результатов, чем аналогичный алгоритм с использованием определителя. |
|||||||||||||||||
|
|
|||||||||||||||||

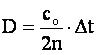

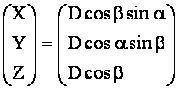
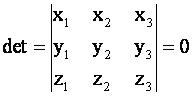
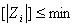

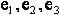 – система, в которой находится плоскость; система координат x,y,z – это система координат, в которой точки лежат в плоскости ху.
– система, в которой находится плоскость; система координат x,y,z – это система координат, в которой точки лежат в плоскости ху.
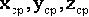 ) по каждой из координат. Получим матрицу А, все точки которой будут рассеяны относительно центра тяжести:
) по каждой из координат. Получим матрицу А, все точки которой будут рассеяны относительно центра тяжести: